2.5: Medición de la Altura en Árboles Irregulares
- Page ID
- 52814
Consideraciones sobre especies: Es bastante fácil medir la altura de los árboles en las coníferas porque las coníferas tienen una parte superior muy distinta. El verticilo de crecimiento de cada año produce una punta clara con ramas laterales cortas, incluso en cicutas (Tsuga spp.) (Figura 2.8).

Figura 2.8. Las coníferas tienen partes superiores claras y distintivas que facilitan la búsqueda de la parte superior.

Figura 2.9. Maderas duras como este encino (Quercus kelloggii) tienen coronas redondeadas o irregulares que pueden dificultar un poco más la búsqueda de la parte superior.
Las maderas duras por otro lado, tienen coronas redondeadas que a menudo son función de la cantidad de sol que son capaces de capturar (Figura 2.9). Bajo condiciones de sombra, pueden ser muy unilaterales. En maderas duras, es sumamente importante obtener una visión clara de toda la corona, para que las ramas laterales no se confundan con la parte superior.
Tops rotos
Los árboles en los que se ha volado la cima pueden ser difíciles. La punta corta o inexistente suele estar oculta por largas ramas laterales cerca de la parte superior del árbol. Si la parte superior no se puede ver con claridad, es fácil confundir las puntas de las ramas laterales con la parte superior. Una parte superior redondeada o plana en una conífera sugiere que falta una parte superior, y este tipo de árbol siempre debe examinarse de cerca (Figura 2.10). Como vimos en la Figura 2.6, medir una rama lateral en lugar de la punta puede sobreestimar la altura del árbol. Cuanto más cerca está el árbol, mayor es el error. Esta es otra razón por la que es importante caminar una distancia lo suficientemente lejos del árbol para obtener una visión clara de la cima.

Figura 2.10. Un abeto de copa plana. Cuando las coníferas tienen tales cimas de “nido de águila”, indica que el tallo principal se ha desprendido del árbol. Observe qué tan grande es el diámetro en este punto.
Al medir la altura total en árboles con copas rotas, la parte superior del árbol debe ser “reconstruida”, para mantener la forma correcta del árbol, o “original”. La conicidad incorrecta afectará las estimaciones de volumen de madera. Un árbol normal que mide 124' de altura (A abajo) tiene una forma muy diferente a la de un árbol cuya parte superior se ha roto a 124' (B abajo). El método estándar para reconstruir la parte superior de un árbol es observar los árboles circundantes y estimar la altura faltante del árbol roto a partir de su crecimiento. Digamos que un árbol similar en diámetro y ahusamiento al árbol de la parte superior rota de abajo (C abajo), corre 20 pies desde un diámetro de cinco pulgadas hasta su punta (Figura 2.11). Usando esto como guía, uno podría agregar 20 pies al árbol con la parte superior rota para una altura total reconstruida de 144 pies.
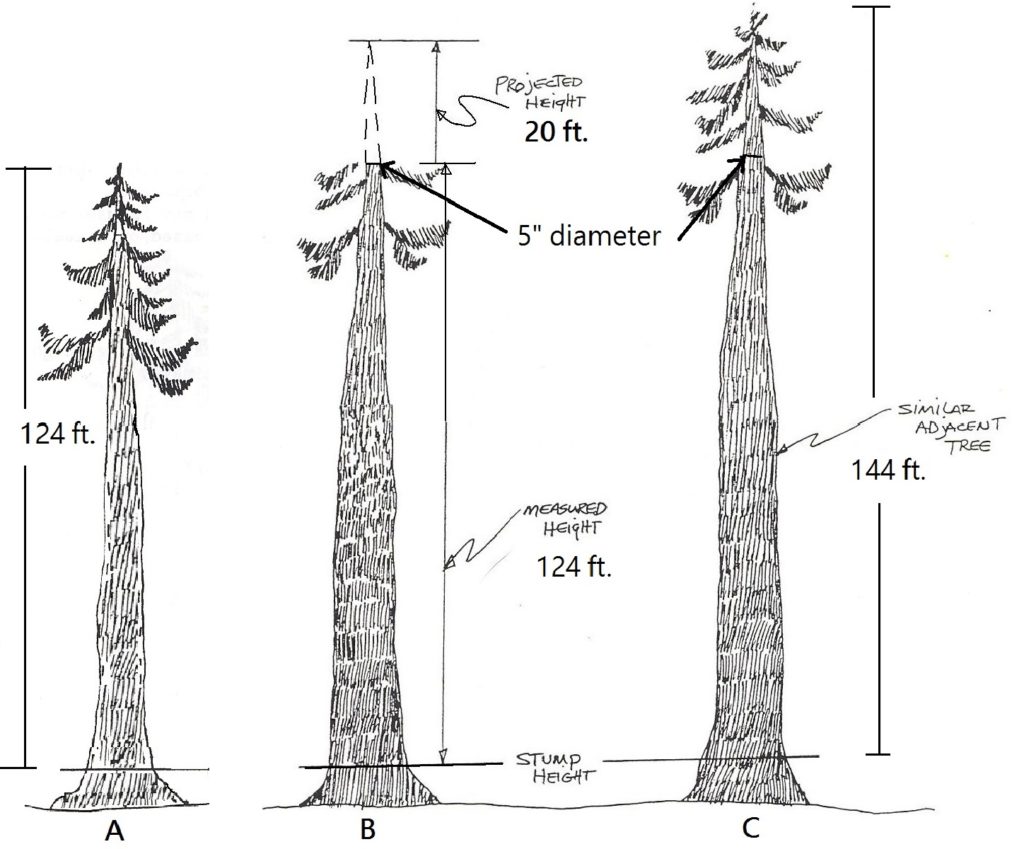
Figura 2.11. Para estimar cuánta altura agregar a un árbol con la parte superior rota, se mide un árbol vecino que es similar en tamaño y ahusamiento y se usa como guía. En este ejemplo, la parte superior estalló a un diámetro de 5 pulgadas. Un árbol similar se midió desde un diámetro de 5 pulgadas hasta su parte superior. Esta longitud era de 20 pies. Por lo tanto, se agregaron 20 pies para “reconstruir” la parte superior del árbol roto para una altura total de 144 pies. (Adaptado de [FS] 1990.)
Árboles inclinados
Para un árbol inclinado, tenemos que ajustar nuestra imagen del triángulo árbol-tierra. En este caso, el árbol inclinado es la hipotenusa del triángulo en lugar de la subida (Figura 2.12). La altura del árbol se puede estimar utilizando el Teorema de Pitágoras y los siguientes pasos:
- Mida una distancia horizontal desde la punta del árbol hasta que esté claramente a la vista.
- Calcular la distancia perpendicular desde la punta del árbol hasta el suelo (subida), usando lecturas de %pendiente como antes.
- Mida la distancia horizontal desde la caída perpendicular a la base del árbol (la carrera).
- Una vez determinados estos dos lados del triángulo, estime la altura total del árbol utilizando el Teorema de Pitágoras para resolver la hipotenusa.
Vea el ejemplo en la Figura 2.12 a continuación:
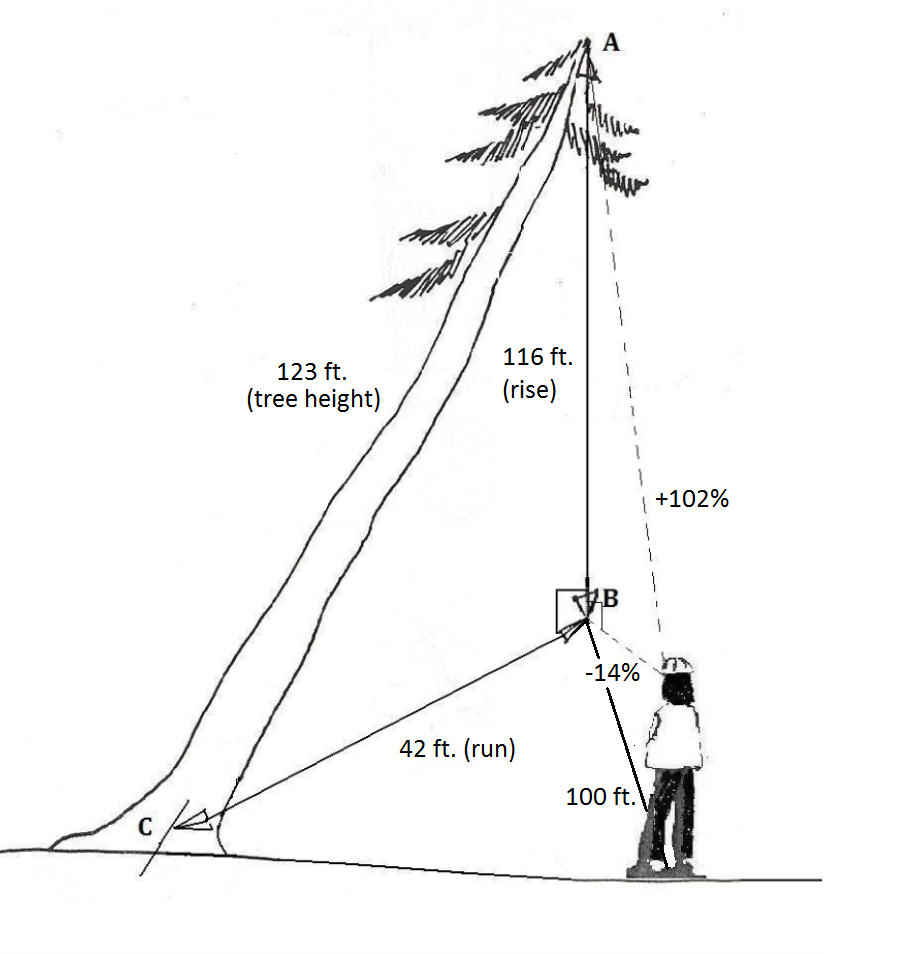
Figura 2.12. Se determina la altura total de un árbol más delgado. (Dibujo adaptado de [FS] 1990.)
1. El técnico sale a una distancia horizontal de la línea de caída AB (en este caso 100 pies).
2. Se toma una lectura de% de pendiente a la punta del árbol (A, +102%), y luego al punto en el suelo donde la línea de caída AB cruza el suelo (B, (-14%). Usando las lecturas de dos %pendiente, se determina el ascenso del triángulo; en este caso, 116 pies.
3. La distancia horizontal entre el Punto B y el muñón del árbol (C) se mide con una cinta para determinar el recorrido; en este caso 42 pies.
4. Finalmente, utilizando el Teorema de Pitágoras, se puede determinar la hipotenusa o la altura del árbol.

o
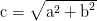
por lo
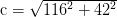
y
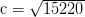
c = 123 pies.
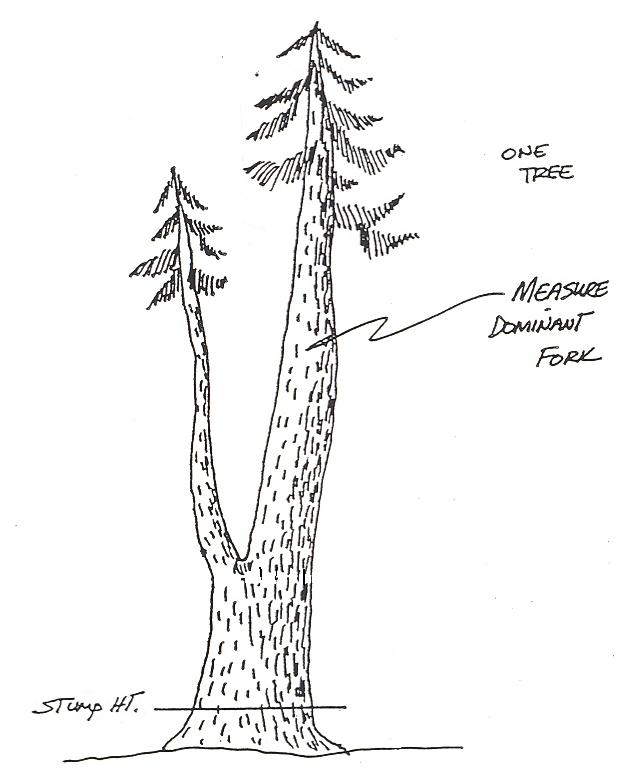
Figura 2.13. En árboles bifurcados, la altura total se mide desde el tocón hasta la punta del tenedor más alto. (De [FS] 1990.)
Árboles bifurcados
En árboles bifurcados, se mide el tenedor más alto o dominante (Figura 2.13). En algunos casos, el segundo tenedor ocurre lo suficientemente bajo en el árbol como para ser contado como un segundo árbol, pero para la mayoría de los árboles, el tenedor más alto es el único tenedor comerciable.


