3: Estructura poblacional y correlaciones entre loci
- Page ID
- 58123
Los individuos rara vez se aparean completamente al azar tus padres no eran dos Bilateria arrancados al azar del árbol de la vida. Incluso dentro de las especies, a menudo hay apareamiento restringido geográficamente entre los individuos. Los individuos tienden a aparearse con individuos de la misma o grupos de poblaciones estrechamente relacionados. Esta forma de apareamiento no aleatorio se denomina estructura poblacional y puede tener profundos efectos en la distribución de la variación genética dentro y entre las poblaciones naturales.
Las poblaciones a menudo pueden diferir en sus frecuencias alélicas, ya sea debido a la deriva genética o la selección que impulsa la diferenciación entre poblaciones. En este capítulo hablaremos a través de algunas formas de resumir y visualizar la estructura genética de la población. La diferenciación poblacional es también un importante impulsor de correlaciones en estado alélico entre los loci, y comenzaremos nuestra discusión sobre estas correlaciones al final de este capítulo. Una razón para hablar de la estructura poblacional tan temprano en el libro es que resumir la estructura poblacional suele ser una etapa inicial clave en los análisis genómicos poblacionales. Por lo tanto, a menudo encontrarás resúmenes y visualizaciones de la estructura de la población cuando leemos trabajos de investigación, por lo que es bueno tener alguna comprensión de lo que representan.
La endogamia como resumen de la estructura poblacional
Nuestras declaraciones sobre la endogamia y los coeficientes de endogamia representan una forma natural de resumir la estructura poblacional. En el capítulo anterior, definimos la endogamia como tener padres que están más estrechamente relacionados entre sí que dos individuos extraídos al azar de alguna población de referencia. La pregunta que surge naturalmente es: ¿Qué población de referencia debemos utilizar? Si bien podría no parecer endogámico en comparación con las frecuencias alélicas en el Reino Unido (Reino Unido), de donde soy, mis padres ciertamente no son dos individuos dibujados al azar de la población mundial. Si estimaremos mi coeficiente de endogamia\(F\) usando frecuencias alélicas dentro del Reino Unido, estaría cerca de cero, pero probablemente sería mayor si usáramos frecuencias mundiales. Esto se debe a que hay un nivel algo menor de heterocigosidad esperada dentro del Reino Unido que en la población humana en todo el mundo en su conjunto.
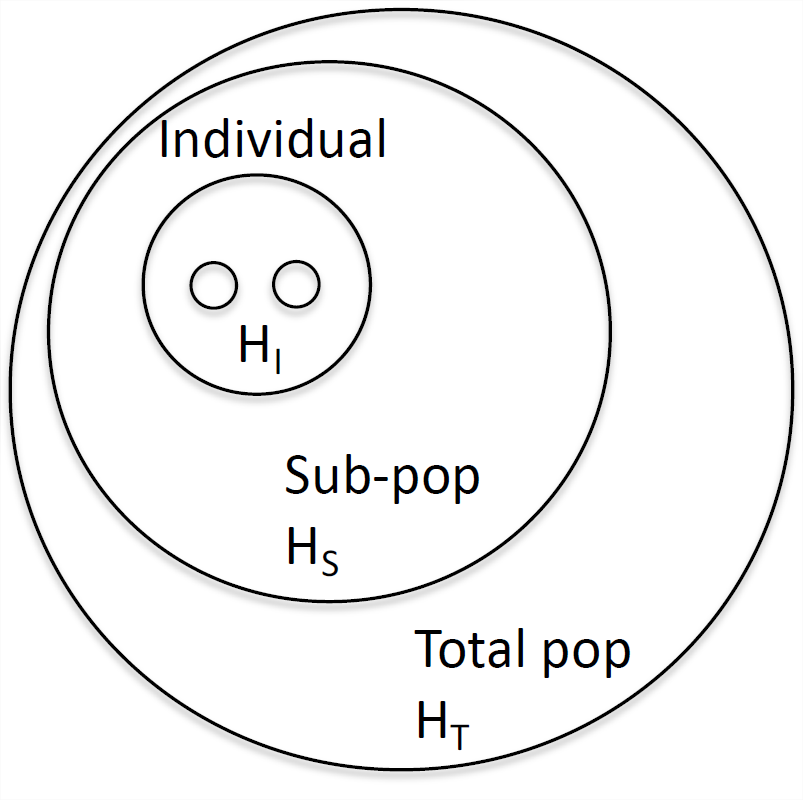
A partir de esta idea de coeficientes de endogamia estimados en varios niveles, se desarrolló un conjunto de 'estadísticas F' (también llamadas 'índices de fijación') que formalizan la idea de endogamia con respecto a diferentes niveles de estructura poblacional. Consulte la Figura\(\PageIndex{1}\) para ver un diagrama esquemático. Wright definió\(F_{\mathrm{XY}}\) como la correlación entre gametos aleatorios, extraídos del mismo nivel\(X\), en relación con el nivel\(Y\). Volveremos a por qué\(F\) -las estadísticas son declaraciones sobre correlaciones entre alelos en tan solo un momento. Una\(F\) estadística de uso común es\(F_{\mathrm{IS}}\), que es el coeficiente de endogamia entre un individuo (\(I\)) y la subpoblación (\(S\)). Considera un solo locus, donde en una subpoblación (\(S\)) una fracción\(H_I=f_{12}\) de individuos son heterocigotos. En esta subpoblación, dejemos que la frecuencia del alelo\(A_1\) sea\(p_S\), tal que sea la heterocigosidad esperada bajo apareamiento aleatorio\(H_S = 2 p_S (1 - p_S)\). Escribiremos\(F_{\mathrm{IS}}\) como
\[F_{\mathrm{IS}} = 1-\frac{H_I}{H_S}= 1-\frac{f_{12}}{2p_Sq_S}, \label{eqn:FIS}\]
un análogo directo de\ ref {eqn:fhat}. Por lo tanto,\(F_{\mathrm{IS}}\) es la diferencia relativa entre heterocigosidad observada y esperada debido a una desviación del apareamiento aleatorio dentro de la subpoblación. También se pudo comparar la heterocigosidad observada en individuos (\(H_I\)) con la esperada en la población total,\(H_T\). Si la frecuencia del alelo\(A_1\) en la población total es\(p_T\), entonces podemos escribir\(F_{\mathrm{IT}}\) como
\[F_{\mathrm{IT}} =1-\frac{H_I}{H_T}= 1-\frac{f_{12}}{2p_Tq_T}, \label{eqn:FIT}\]
que compara la heterocigosidad en individuos con la esperada en la población total. Como simple extensión de esto, podríamos imaginar comparar la heterocigosidad esperada en la subpoblación (\(H_S\)) con la esperada en la población total\(H_T\), a través de\(F_{\mathrm{ST}}\):
\[F_{\mathrm{ST}} = 1-\frac{H_S}{H_T}=1-\frac{2p_Sq_S}{2p_Tq_T} \label{eqn:FST}.\]
Podemos relacionar las tres\(F\) estadísticas entre sí como
\[(1-F_{\mathrm{IT}}) =\frac{H_I}{H_S} \frac{H_S}{H_T}=(1-F_{\mathrm{IS}})(1-F_{\mathrm{ST}}). \label{eqn:F_relationships}\]
De ahí que la reducción de la heterocigosidad dentro de los individuos en comparación con la esperada en la población total se puede descomponer a la reducción de la heterocigosidad de los individuos en comparación con la subpoblación, y la reducción de la heterocigosidad de la población total a la de la subpoblación.
Si queremos un resumen de la estructura poblacional en múltiples subpoblaciones, podemos promediar\(H_I\) y/o\(H_S\) entre poblaciones, y usar un\(p_T\) cálculo promediando\(p_S\) entre subpoblaciones (o nuestras muestras de subpoblaciones). Por ejemplo, el promedio\(\bar{F_{\mathrm{ST}}}\) entre\(K\) subpoblaciones (muestreadas con igual esfuerzo) es
\[\bar{F_{\mathrm{ST}}} = 1 - \frac{\bar{H}_{S}}{H_T},\]
donde\(\bar{H}_S = \frac{1}{K} \sum_{i = 1}^{K} H_{S}^{(i)}\), y\(H_{S}^{(i)} = 2 p_{i} q_{i}\) es la heterocigosidad esperada en la subpoblación\(i\). De ello se deduce que la heterocigosidad promedio de las subpoblaciones\(\bar{H}_S \leq H_T\), y así\(\bar{F_{\mathrm{ST}}} \geq 0\) y\(\bar{F_{\mathrm{IS}}} \leq \bar{F_{\mathrm{IT}}}\). Esta observación de que la heterocigosidad promedio de las subpoblaciones debe ser menor que igual a la de la población total se denomina efecto Wahlund. Además, si tenemos múltiples sitios, podemos reemplazar,\(H_I\)\(H_S\), y\(H_T\) con sus promedios a través de loci (como arriba).
En una especie de lémures, se estima que la frecuencia alélica es\(20\%\). En una población en particular, se estima que la frecuencia alélica es\(10\%\). En esta población, sólo\(9\%\) de los individuos son heterocigotos. ¿Qué es\(F_{IT}\)\(F_{ST}\), y\(F_{IS}\) para esta población?
Como ejemplo de comparar una estimación de todo el genoma con la de\(F_{ST}\) loci individuales, podemos observar algunos datos de currucas de alas azules y doradas (Vermivora cyanoptera y V. chrysoptera 1-2 y 5-6 en la Figura\ ref {fig:blue_golden_ reinzas}).

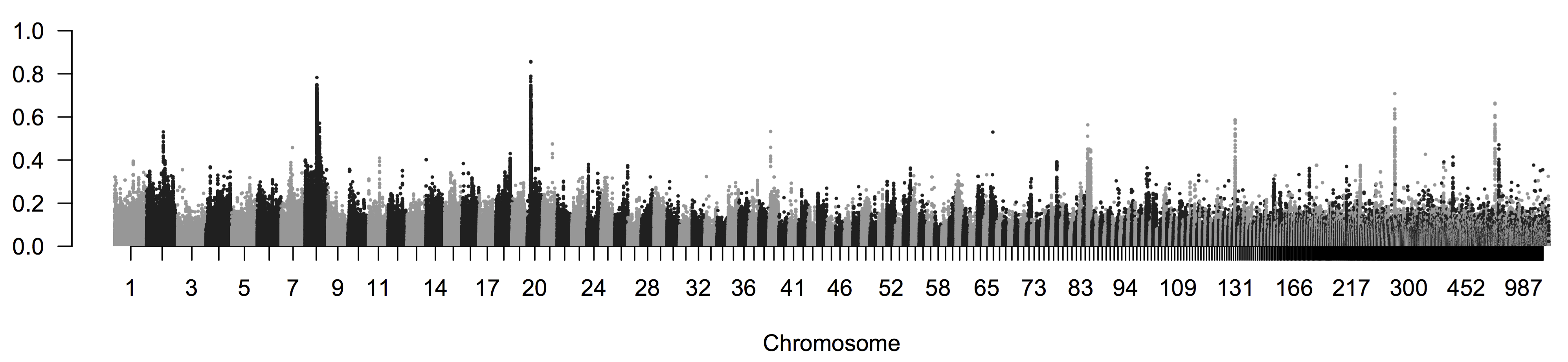
Estas dos especies se encuentran diseminadas por el este de América del Norte, con la curruca de alas doradas que tiene un rango más pequeño y más septentrional. Son bastante diferentes en cuanto al plumaje, pero desde hace tiempo se sabe que tienen canciones y ecologías similares. Las dos especies se hibridan fácilmente en la naturaleza; de hecho, otras dos especies previamente reconocidas, la curruca de Brewster y Lawrence (4 & 3 in\ ref {fig:blue_golden_warblers}), en realidad se encuentra que solo son híbridos entre estas dos especies. La curruca de alas doradas está catalogada como 'amenazada' bajo el acto de especies canadienses en peligro de extinción ya que su hábitat está bajo presión de la actividad humana y y debido a la creciente hibridación con la curruca de alas azules, que se está moviendo hacia el norte hacia su rango. Investigó la genómica poblacional de estas currucas, secuenciando diez currucas de alas doradas y diez currucas de alas azules. Encontraron muy baja divergencia entre estas especies, con un genoma amplio\(F_{ST}=0.0045\). En la Figura\ ref {fig:Warbler_fst}, por SNP\(F_{ST}\) se promedia en ventanas\(2000\) pb que se mueven a lo largo del genoma. El promedio es muy bajo, pero\(F_{ST}\) destacan algunas regiones de muy alto. Casi todas estas regiones corresponden a grandes diferencias de frecuencia de alelos en loci dentro o cerca de genes que se sabe que están involucrados en las diferencias de coloración del plumaje en otras aves.
Para ilustrar estas diferencias de frecuencia, Toews et al. (2016) genotiparon un SNP en cada una de estas\(F_{ST}\) regiones altas. Aquí están sus recuentos de genotipado del SNP, segregando para un alelo 1 y 2, en la región Wnt, un gen regulador clave involucrado en el desarrollo de plumas:
| Especies | 11 | 12 | 22 |
| Alas azules | 2 | 21 | 31 |
| Alas doradas | 48 | 12 | 1 |
Con referencia a la tabla de recuentos de alelos Wnt:
- Calcular\(F_{IS}\) en currucas de alas azules.
- Calcular\(F_{ST}\) para la subpoblación de currucas de alas azules en comparación con la muestra combinada.
- Calcular la\(F_{ST}\) media en ambas subpoblaciones.
Interpretaciones de la estadística F
Volvamos ahora a la definición de Wright de la\(F\) -estadística como correlaciones entre gametos aleatorios, extraídos del mismo nivel\(X\), relativo al nivel\(Y\). Sin pérdida de generalidad, podemos pensar\(X\) como individuos y\(S\) como subpoblación. Reescritura\(F_{\mathrm{IS}}\) en términos de las frecuencias observadas de homocigotos (\(f_{11}\),\(f_{22}\)) y homocigosidades esperadas (\(p_{S}^2\),\(q_{S}^2\)) encontramos
\[\begin{aligned} F_{\mathrm{IS}} &= \dfrac{2p_Sq_S - f_{12}}{2p_Sq_S} \\[4pt] &= \dfrac{f_{11}+f_{22} - p_S^2 - q_S^2}{2p_Sq_S}, \label{eqn:Fascorr} \end{aligned}\]
utilizando el hecho de que\(p^2+2pq+q^2=1\), y\(f_{12} = 1 - f_{11} - f_{12}\). La forma de Ecuación\ ref {EQN:FASCORR} revela que\(F_{\mathrm{IS}}\) es la covarianza entre pares de alelos encontrados en un individuo, dividida por la varianza esperada bajo muestreo binomial. Así,\(F\) -estadística puede entenderse como la correlación entre alelos extraídos de una población (o un individuo) por encima de lo esperado por casualidad (es decir, dibujar alelos muestreados al azar de alguna población más amplia).
También podemos interpretar\(F\) -estadísticas como proporciones de varianza explicadas por diferentes niveles de estructura poblacional. Para ver esto, pensemos en\(F_{\mathrm{ST}}\) promediado sobre\(K\) subpoblaciones, cuyas frecuencias son\(p_1,\dots,p_K\). La frecuencia en la población total es\(p_T=\bar{p} = \frac{1}{K} \sum_{i=1}^K p_i\). Entonces, podemos escribir
\[\begin{aligned} F_{\mathrm{ST}} &= \dfrac{2 \bar{p}\bar{q} - \dfrac{1}{K} \displaystyle \sum_{i=1}^K 2p_iq_i }{2 \bar{p}\bar{q}} \\[4pt] &= \dfrac{ \left(\frac{1}{K} \displaystyle \sum_{i=1}^K p_i^2 + \dfrac{1}{K} \displaystyle \sum_{i=1}^K q_i^2 \right) - \bar{p}^2-\bar{q}^2 }{2 \bar{p}\bar{q}} \nonumber\\[4pt] &= \dfrac{\mathrm{Var}(p_1,\dots,p_K)}{\mathrm{Var}(\bar{p})}, \label{eqn:F_as_propvar}\end{aligned}\]
lo que muestra que\(F_{\mathrm{ST}}\) es la proporción de la varianza explicada por las etiquetas de subpoblación.
Otros enfoques de la estructura de la población
Existe un amplio espectro de métodos para describir patrones de estructura poblacional en conjuntos de datos genéticos poblacionales. Discutiremos brevemente dos clases amplias de métodos que aparecen a menudo en la literatura: métodos de asignación y análisis de componentes principales.
Métodos de Asignación
Aquí describiremos una simple asignación probabilística para encontrar la probabilidad de que un individuo de población desconocida provenga de una de las poblaciones\(K\) predefinidas. Por ejemplo, hay tres amplias poblaciones de chimpancé común (Pan troglodytes) en África: occidental, central y oriental. Imagínese que tenemos un chimpancé cuya población de origen es desconocida (por ejemplo, es de una colección privada ilegal). Si hemos genotipado un conjunto de marcadores no enlazados de un panel de individuos representativos de estas poblaciones, podemos calcular la probabilidad de que nuestro chimpancé provenga de cada una de estas poblaciones.
Luego explicaremos brevemente cómo extender esta idea para agrupar un conjunto de individuos en poblaciones\(K\) inicialmente desconocidas. Este método es una versión simplificada de lo que hacen los algoritmos de agrupamiento de genética de poblaciones como ESTRUCTURA y ADMIZCEL.
Un método de asignación simple
Tenemos datos de genotipos de loci\(S\) bialélicos no enlazados para\(K\) poblaciones. La frecuencia alélica del alelo\(A_1\) en el locus\(l\) en población\(k\) se denota por\(p_{k,l}\), de manera que las frecuencias alélicas en la población 1 son\(p_{1,1},\cdots p_{1,L}\) y la población 2 son\(p_{2,1},\cdots p_{2,L}\) y así sucesivamente.
Se genotipa a un nuevo individuo de una población desconocida en estos\(L\) loci. El genotipo de este individuo en el locus\(l\) es\(g_l\), donde\(g_l\) denota el número de copias del alelo que lleva\(A_1\) este individuo en este locus (\(g_l=0,1,2\)).
La probabilidad de que el genotipo de este individuo en el locus esté\(l\) condicionado a provenir de la población\(k\), es decir, que sus alelos sean un sorteo aleatorio de HW de la población\(k\), es
\[\mathbb{P}(g_l | \textrm{pop k}) = \begin{cases} (1-p_{k,l})^2 & g_l=0 \\ 2 p_{k,l} (1-p_{k,l}) & g_l=1\\ p_{k,l}^2 & g_l=2 \end{cases}\]
Suponiendo que los loci son independientes, la probabilidad del genotipo del individuo en todos los loci S, condicionada a que el individuo provenga de la población\(k\), es
\[\mathbb{P}(\textrm{ind.} | \textrm{pop k}) = \prod_{l=1}^S \mathbb{P}(g_l | \textrm{pop k}) \label{eqn_assignment}\]
Deseamos conocer la probabilidad de que este nuevo individuo provenga de población\(k\), i.e\(P(\textrm{pop k} | \textrm{ind.})\). Podemos obtener esto a través del gobierno de Bayes
\[\mathbb{P}(\textrm{pop k} | \textrm{ind.}) = \frac{\mathbb{P}(\textrm{ind.} | \textrm{pop k}) \mathbb{P}(\textrm{pop k})}{\mathbb{P}(\textrm{ind.})}\]
donde
\[\mathbb{P}(\textrm{ind.}) = \sum_{k=1}^K \mathbb{P}(\textrm{ind.} | \textrm{pop k}) \mathbb{P}(\textrm{pop k})\]
es la constante normalizadora. Podemos interpretar\(\mathbb{P}(\textrm{pop k})\) como la probabilidad previa de que el individuo provenga de la población\(k\), y a menos que tengamos algún otro conocimiento previo asumiremos que el nuevo individuo tiene la misma probabilidad de provenir de cada población\(\mathbb{P}(\textrm{pop k})=\frac{1}{K}\).
Interpretamos
\[\mathbb{P}(\textrm{pop k} | \textrm{ind.})\]
como la probabilidad posterior de que nuestro nuevo individuo provenga de cada una de nuestras\(1,\cdots, K\) poblaciones.
Versiones más sofisticadas de esto ahora se utilizan para permitir híbridos, por ejemplo, podemos tener una proporción\(q_k\) del genoma de nuestro individuo proviene de la población\(k\) y estimar el conjunto de\(q_k\)'s.
Volviendo a nuestro ejemplo de chimpancé, imaginemos que hemos genotipado un conjunto de individuos de las poblaciones occidental y oriental en dos SNP (ignoraremos a la población central para simplificar las cosas). La frecuencia del alelo capital en dos SNP (\(A/a\)y\(B/b\)) viene dada por
| Población | locus A | locus B |
|---|---|---|
| Western | \(0.1\) | \(0.85\) |
| Oriental | \(0.95\) | \(0.2\) |
- Nuestro individuo, cuyo origen es desconocido, tiene el genotipo\(AA\) en el primer locus y\(bb\) en el segundo. ¿Cuál es la probabilidad posterior de que nuestro individuo provenga de la población occidental versus la población de chimpancés orientales?
- (Más complicado) Supongamos que nuestro individuo de la parte A es un híbrido (no necesariamente un F1). En cada locus, con probabilidad\(q_W\) nuestro individuo dibuja un alelo de la población occidental y con probabilidad\(q_E=1-q_W\) dibuja un alelo de la población oriental. ¿Cuál es la probabilidad del genotipo de nuestro individuo dada\(q_W\)?
Opcional Podría trazar esta probabilidad en función de\(q_W\). ¿Cómo cambia tu parcela si nuestro individuo es heterocigoto en ambos loci?
Agrupación basada en métodos de asignación
Si bien es genial poder asignar a nuestros individuos a una población en particular, estas ideas pueden ser empujadas para aprender sobre la mejor manera de describir nuestros datos de genotipos en términos de poblaciones discretas sin asignar ninguno de nuestros individuos a poblaciones a priori. Deseamos agrupar a nuestros individuos en poblaciones\(K\) desconocidas. Comenzamos asignando nuestros individuos al azar a estas\(K\) poblaciones.
- Dadas estas asignaciones, estimamos las frecuencias alélicas en todos nuestros loci en cada población.
- Dadas estas frecuencias alélicas, elegimos reasignar cada individuo a una población\(k\) con una probabilidad dada por\ ref {eqn_assignment}.
Iteramos los pasos 1 y 2 para muchas iteraciones (técnicamente, este enfoque se conoce como Gibbs Sampling). Si los datos son suficientemente informativos, las asignaciones y frecuencias alélicas convergerán rápidamente en un conjunto de probables asignaciones poblacionales y frecuencias alélicas para estas poblaciones.

[fig:chimp_structure]
Para hacer esto en un esquema bayesiano completo necesitamos colocar antecedentes en las frecuencias alélicas (por ejemplo, se podría usar una distribución beta previa). Técnicamente estamos utilizando la articulación posterior de nuestras frecuencias alélicas y asignaciones. Programas como ESTRUCTURA, utilizan este tipo de algoritmo para agrupar a los individuos de una manera “no supervisada” (es decir, resuelven cómo asignar individuos a un conjunto desconocido de poblaciones). Consulte la Figura\ ref {fig:chimp_structure} para ver un ejemplo del uso de ESTRUCTURA para determinar la estructura poblacional de los chimpancés.
Los métodos similares a la estructura han demostrado ser increíbles y útiles en el examen de la estructura poblacional dentro de las especies. Sin embargo, los resultados de estos métodos están abiertos a malas interpretaciones; véase para una discusión reciente. Dos errores comunes son 1) tomar los resultados de enfoques similares a la estructura para algún valor particular de K y tomar esto para representar la mejor manera de describir la variación población-genética. 2) Pensar que estos racimos representan poblaciones ancestrales 'puras'.
No hay una elección correcta de K, el número de clústeres en los que particionar. Existen métodos para juzgar la 'mejor' K por alguna medida estadística dado algún conjunto de datos en particular, pero eso no es lo mismo que decir que este es el nivel más significativo sobre el que resumir la estructura poblacional en los datos. Por ejemplo, ejecutar ESTRUCTURA en poblaciones humanas mundiales para obtener un valor bajo de K dará como resultado grupos de población que se alineen aproximadamente con las poblaciones continentales. Sin embargo, eso no nos dice que asignar ascendencia a nivel de continentes sea una forma particularmente significativa de particionar a los individuos. Ejecutar los mismos datos para un mayor valor de K, o dentro de las regiones continentales, resultará en una partición de grupos continentales a una escala mucho más fina. Ninguna de estas capas de estructura poblacional identificadas tiene el privilegio de ser más significativa que otra.
Es tentador pensar que estos racimos representan poblaciones ancestrales, que en sí mismas no son el resultado de la mezcla. Sin embargo, ese no es el caso, por ejemplo, ejecutar ESTRUCTURA sobre datos humanos mundiales identifica un cluster que contiene muchos individuos europeos, sin embargo, sobre la base del ADN antiguo sabemos que los europeos modernos son una mezcla de distintos grupos ancestrales.
Análisis de componentes principales
El análisis de componentes principales (PCA) es un enfoque estadístico común para visualizar datos de alta dimensión, y utilizado por muchos campos. La idea de PCA es dar una ubicación a cada punto de datos individual en cada uno de un número pequeño de ejes de componentes principales. Estos ejes de PC se eligen para reflejar los principales ejes de variación en los datos, siendo el primer PC el que explica la mayor varianza, el segundo el segundo más, y así sucesivamente. El uso de PCA en genética de poblaciones fue pionero por Cavalli-Sforza y colegas y ahora con grandes conjuntos de datos de genotipado, PCA ha regresado.
Considere un conjunto de datos que consiste en N individuos en SNP\(S\) bialélicos. Los datos del genotipo del\(i^{th}\) individuo en el locus\(\ell\) toman un valor\(g_{i,\ell}=0,1,\; \text{or} \; 2\) (correspondiente al número de copias del alelo que lleva\(A_1\) un individuo en este SNP). Podemos pensar en esto como una\(N \times S\) matriz (donde usualmente\(N \ll S\)).
Denotando la frecuencia media del alelo de la muestra en SNP\(\ell\) por\(p_{\ell}\), es común estandarizar el genotipo de la siguiente manera
\[\frac{g_{i,\ell} - 2 p_{\ell}}{\sqrt{2 p_{\ell}(1-p_{\ell})}} \label{eqn:std_allele_freq}\]
es decir, en cada SNP centramos los genotipos restando el genotipo medio (\(2p_{\ell}\)) y dividimos por la raíz cuadrada de la varianza esperada asumiendo que los alelos se muestrean binomialmente de la frecuencia media (\(\sqrt{2 p_{\ell} (1-p_{\ell})}\)). Haciendo esto a todos nuestros genotipos, formamos una matriz de datos (de dimensión\(N \times S\)). Luego podemos realizar análisis de componentes principales de esta matriz de datos para descubrir los ejes principales de varianza del genotipo en nuestra muestra. La Figura\ ref {fig:chimp_pca} muestra un PCA usando los mismos datos de chimpancé que en la Figura\ ref {fig:chimp_structure}.
![Análisis de componentes principales mediante el uso de los mismos datos de chimpancé que en la Figura [fig:chimp_structure]. Aquí traza la ubicación de cada individuo en los dos primeros componentes principales (llamados vectores propios) en el panel izquierdo, y en el segundo y tercer componentes principales (vectores propios) en el panel derecho (). En el PCA, los individuos identificados como todos de una ascendencia por ESTRUCTURA se agrupan por población (círculos sólidos). Mientras que los nueve individuos identificados por ESTRUCTURA como híbridos (círculos abiertos) en su mayor parte caen en ubicaciones intermedias en el PCA. Hay dos individuos (círculos abiertos rojos) reportados como de una población en particular pero que pero parecen ser híbridos.](/figures/Becquet_et_al_STRUCTURE_journal_pgen_0030066_g002.png)
[fig:chimp_pca]
Vale la pena tomarse un momento para profundizar en lo que estamos haciendo aquí. Hay una serie de formas equivalentes de pensar sobre lo que está haciendo PCA. Una de estas formas es pensar que cuando hacemos PCA estamos construyendo el individuo por matriz de covarianza individual y realizando una descomposición de valores propios de esta matriz (siendo los vectores propios los PCs). Esta matriz de covarianza individual por individuo tiene entradas\([i,~j]\) dadas por
\[\frac{1 }{S-1} \sum_{\ell=1}^S \frac{(g_{i,\ell} - 2p_{\ell})(g_{j,\ell} - 2p_{\ell})}{2 p_{\ell}(1-p_{\ell})} \label{eqn:kinship_mat}\]
Tenga en cuenta que esta es la covarianza muestral de nuestras frecuencias alélicas estandarizadas (\ ref {eqn:std_allele_freq}), y es muy similar a las que encontramos al discutir\(F\) -estadística como correlaciones (\ ref {EQN:FASCORR}), excepto que ahora estamos preguntando sobre la covarianza entre dos individuos arriba que esperaban si ambos fueran extraídos de la muestra total al azar (en lugar de la covarianza de alelos dentro de un solo individuo). Entonces, al realizar PCA sobre los datos estamos aprendiendo sobre los ejes mayores (ortogonales) de la matriz de parentesco.
Como ejemplo de la aplicación de PCA, consideremos el caso de las supuestas especies de anillos en el complejo de especies de curruca verdosa (Phylloscopus trochiloides). Este conjunto de subespecies existe en un anillo alrededor del borde de la meseta del Himalaya. Se recolectaron muestras de curruca\(95\) verdosa de\(22\) sitios alrededor del anillo, y las ubicaciones de muestreo se muestran en la Figura\ ref {fig:Gwarbler_geo}.

[Fig:Gwarbler_geo]
Se piensa que estas currucas se extendieron desde el sur, hacia el norte en dos direcciones diferentes alrededor de la inhóspita meseta del Himalaya, estableciendo poblaciones a lo largo del borde occidental (poblaciones verdes y azules) y el borde oriental (poblaciones amarillas y rojas). Cuando entraron en contacto secundario en Siberia, se aislaron reproductivamente entre sí, habiendo evolucionado diferentes canciones y acumulando otras barreras reproductivas entre sí a medida que se extendían independientemente al norte alrededor de la meseta, de tal manera que P. t. viridanus (azul) y Las poblaciones de P. t. plumbeitarsus (rojo) forman actualmente una zona híbrida estable.

[fig:curruca verdosa]
obtuvieron datos de secuencia para sus muestras a 2,334 snps. En la Figura\ ref {fig:warbler_heat} se puede ver la matriz de coeficientes de parentesco, usando\ ref {eqn:kinship_mat}, entre todos los pares de muestras. Ya se puede ver mucho sobre la estructura poblacional en esta matriz. Observe cómo las muestras rojas y amarillas, que se cree derivan de la ruta oriental alrededor del Himalaya, tienen mayor parentesco entre sí, y el azul y la (mayoría) de las muestras verdes, de la ruta occidental, forman un grupo similar cercano en términos de su parentesco superior.
![La matriz de coeficientes de parentesco calculados para las 95 muestras de currucas verdosas. Cada celda en la matriz da el coeficiente de parentesco por pares calculado para un par particular. Colores más calientes que indican mayor parentesco. Las etiquetas x e y de los individuos son las etiquetas poblacionales de la Figura [Fig:Gwarbler_geo], y coloreadas por etiqueta de subespecie como en esa figura. Las filas y columnas se han organizado para agrupar individuos con alto parentesco.](/figures/warbler_PCA_figs/warbler_heatmap.png)
[fig:curruca_calor]
Luego podemos realizar PCA en esta matriz de parentesco para identificar los principales ejes de variación en el conjunto de datos. La Figura\ ref {fig:Warbler_PCA} muestra las muestras trazadas en las dos primeras PC.
![Las 95 muestras de curruca verdosa se trazaron en sus ubicaciones en los dos primeros componentes principales. Las etiquetas de los individuos son las etiquetas poblacionales de la Figura [Fig:Gwarbler_geo], y coloreadas por etiqueta de subespecie como en esa figura.](/figures/warbler_PCA_figs/warbler_PCAmap.jpg)
[Fig:Warbler_PCA]
Las dos principales rutas de expansión ocupan claramente diferentes partes del espacio de PC. El primer componente principal distingue a las poblaciones que corren de norte a sur a lo largo de la ruta occidental de expansión, mientras que el segundo componente principal distingue entre poblaciones que corren de norte a sur a lo largo de la ruta de expansión oriental. Así, los datos genéticos apoyan la hipótesis de que las currucas verdosas especiaron mientras se movían alrededor de la meseta del Himalaya. Sin embargo, como lo señala, también sugiere complicaciones adicionales a la visión tradicional de estas currucas como una especie de anillo ininterrumpido, un caso de especiación por aislamiento geográfico continuo. La subespecie Ludlowi presenta una ruptura genética significativa, con las muestras más meridionales de MN agrupadas con la subespecie Trochiloides, tanto en la PCA como en la matriz de parentesco (Figuras\ ref {fig:Warbler_PCA} y\ ref {fig:warbler_heat}), a pesar de ser mucho más geográficamente cerca de las otras muestras de Ludlowi. Esto sugiere que el aislamiento genético no es solo el resultado de la distancia geográfica, y se deben considerar otras barreras biogeográficas en el caso de esta especie de anillo roto.
Por último, si bien el PCA es una herramienta maravillosa para visualizar datos genéticos, se debe tener cuidado en su interpretación. La forma de U en el caso de la curruca verdosa PC podría ser consistente con un bajo nivel de flujo de genes entre las poblaciones roja y azul, acercándolas genéticamente y ayudando a formar un anillo genético así como un anillo geográfico. Sin embargo, se espera que aparezcan formas similares a U en los PCA incluso si nuestras poblaciones están simplemente alineadas a lo largo de una línea, y arreglos geométricos más complejos de poblaciones en el espacio de PC pueden resultar bajo modelos geográficos simples. Inferir la historia geográfica y población-genética de las especies requiere la aplicación de una variedad de herramientas; ver y para más discusión sobre las currucas verdosas.
Correlaciones entre loci, desequilibrio de ligamiento y recombinación
Hasta ahora nos han interesado las correlaciones entre alelos en un mismo locus, por ejemplo, correlaciones dentro de individuos (endogamia) o entre individuos (parentesco). Hemos visto cómo la relación entre los padres afecta la medida en que su descendencia es endogámica. Pasamos ahora a las correlaciones entre alelos en diferentes loci.
Recombinación
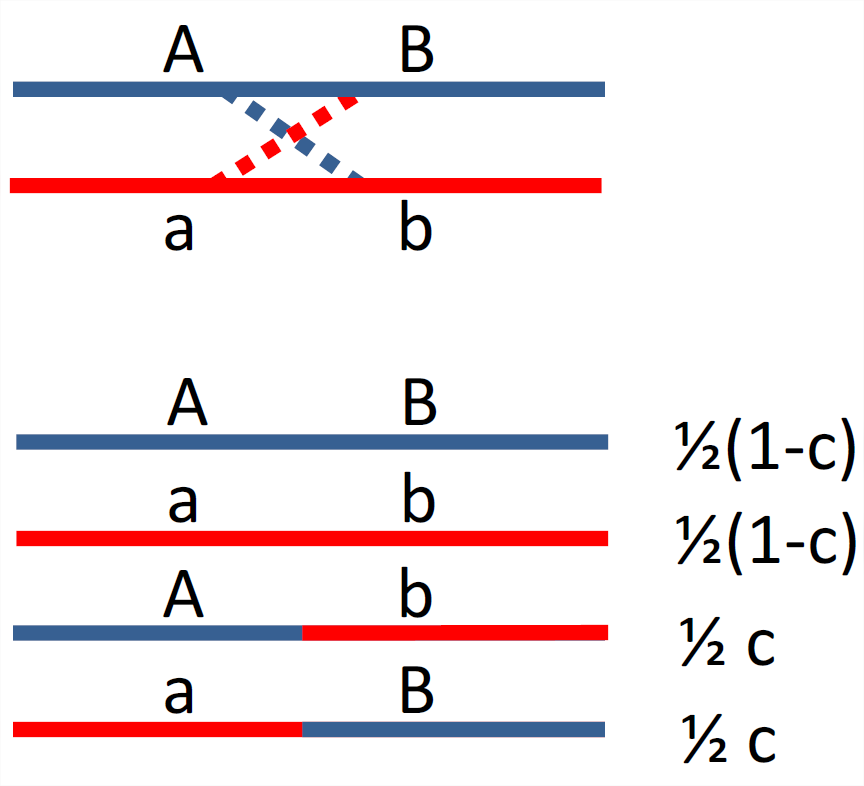
Para entender las correlaciones entre loci necesitamos entender la recombinación un poco más cuidadosamente. Consideremos un individuo heterocigótico, conteniendo\(AB\) y\(ab\) haplotipos. Si no se produce recombinación entre nuestros dos loci en este individuo, entonces estos dos haplotipos se transmitirán intactos a la siguiente generación. Mientras que si se produce una recombinación (es decir, un número impar de eventos de cruce) entre los dos haplotipos parentales, entonces\(\frac{1}{2}\) la hora en que el niño recibe un\(Ab\) haplotipo y\(\frac{1}{2}\) la hora en que el niño recibe un\(aB\) haplotipo. Ver Figura\ ref {fig:recom_cartoon}. Efectivamente, la recombinación rompe la asociación entre loci. Para los marcadores enlazados definimos la fracción de recombinación (\(x\)) como la probabilidad de un número impar de eventos cruzados entre nuestros loci en una sola meiosis. La fracción de recombinación entre un par de loci puede variar de\(0\) a\(\frac{1}{2}\), con los marcadores\(c=\frac{1}{2}\) correspondientes lo suficientemente separados en un cromosoma para que ocurran muchos eventos de recombinación entre ellos (los loci en diferentes automosomas también tienen un \(c=\frac{1}{2}\)). En la práctica, a menudo nos interesarán regiones relativamente cortas de tal manera que la recombinación es relativamente rara, y así podríamos pensar que\(c=c_{BP}L \ll \frac{1}{2}\), ¿dónde\(c_{BP}\) está la tasa promedio de recombinación (en Morgans) por par de bases (típicamente\(\sim 10^{-8}\)) y L es la número de pares de bases que separan nuestros dos loci.
Desequilibrio de ligamiento
La frase (horrible) desequilibrio de ligamiento (LD) se refiere a la no independencia estadística (es decir, una correlación) de alelos en una población en diferentes loci. Es un concepto fantásticamente útil; la LD es clave para comprender diversos temas, desde la selección sexual y especiación hasta los límites de los estudios de asociación de todo el genoma.
Nuestros dos loci bialélicos, que segregan alelos\(A/a\) y\(B/b\), tienen frecuencias alélicas de\(p_A\) y\(p_B\) respectivamente. La frecuencia de los dos locus haplotipo AB es\(p_{AB}\), e igualmente para nuestras otras tres combinaciones. Si nuestros loci fueran estadísticamente independientes entonces\(p_{AB} = p_Ap_B\), de lo contrario,\(p_{AB} \neq p_Ap_B\) podemos definir una covarianza entre los\(B\) alelos\(A\) y en nuestros dos loci como
\[D_{AB} = p_{AB} - p_Ap_B \label{eqn:LD_def}\]
y así mismo para nuestras otras combinaciones en nuestros dos loci (\(D_{Ab},~D_{aB},~D_{ab}\)). Los gametos con dos alelos de casos similares (por ejemplo A y B, o a y b) se conocen como gametos de acoplamiento, y aquellos con diferentes alelos de caso se conocen como gametos de repulsión (por ejemplo, a y B, o A y b). Entonces, podemos pensar en medir\(D\) el exceso de acoplamiento a gametos de repulsión. Estas\(D\) estadísticas están todas estrechamente relacionadas entre sí como\(D_{AB} = - D_{Ab}\) y así sucesivamente. Así solo necesitamos especificar uno\(D_{AB}\) para conocerlos todos, así bajaremos el subíndice y solo nos referiremos a él\(D\). También un resultado útil es que podemos reescribir nuestra frecuencia de haplotipos\(p_{AB}\) como
\[p_{AB} = p_Ap_B+D. \label{eqn:ABviaD}\]
Si\(D=0\) vamos a decir que los dos loci están en equilibrio de ligamiento, mientras que si\(D>0\) o\(D<0\) vamos a decir que los loci están en desequilibrio de ligamiento (tal vez vamos a querer probar si\(D\) es estadísticamente diferente de\(0\) antes de tomar esta decisión). El desequilibrio de ligamiento es una frase horrible, ya que corre el riesgo de confundir los conceptos de vinculación genética y desequilibrio de ligamiento. La vinculación genética se refiere al enlace de múltiples loci debido a que se transmiten a través de la meiosis juntos (la mayoría de las veces porque los loci están en el mismo cromosoma). El desequilibrio de ligamiento se refiere simplemente a la covarianza entre los alelos en diferentes loci; esto puede deberse en parte a la vinculación genética de estos loci pero no necesariamente implica esto (por ejemplo, los loci genéticamente no enlazados pueden estar en LD debido a la estructura poblacional).
Genotipo 2 loci bialélicos (A y B) segregándose en dos subespecies de ratón (1 y 2) que se aparean aleatoriamente entre ellos, pero que históricamente no se han cruzado desde que especiaron. Las frecuencias de haplotipos en cada población son:
| Pop | \(p_{AB}\) | \(p_{Ab}\) | \(p_{aB}\) | \(p_{ab}\) |
|---|---|---|---|---|
| 1 | \ (p_ {AB}\)” style="text-align:center; ">0.02 | \ (p_ {Ab}\)” style="text-align:center; ">0.18 | \ (p_ {aB}\)” style="text-align:center; ">0.08 | \ (p_ {ab}\)” style="text-align:center; ">0.72 |
| 2 | \ (p_ {AB}\)” style="text-align:center; ">0.72 | \ (p_ {Ab}\)” style="text-align:center; ">0.18 | \ (p_ {aB}\)” style="text-align:center; ">0.08 | \ (p_ {ab}\)” style="text-align:center; ">0.02 |
- ¿Cuánto LD hay dentro de las especies? (es decir, estimación D)
- Si mezclamos individuos de las dos especies juntos en proporciones iguales, podríamos formar una nueva población con\(p_{AB}\) igual a la frecuencia promedio de\(p_{AB}\) entre las especies 1 y 2. ¿Qué valor tomaría D en esta nueva población antes de que algún apareamiento haya tenido la oportunidad de ocurrir?
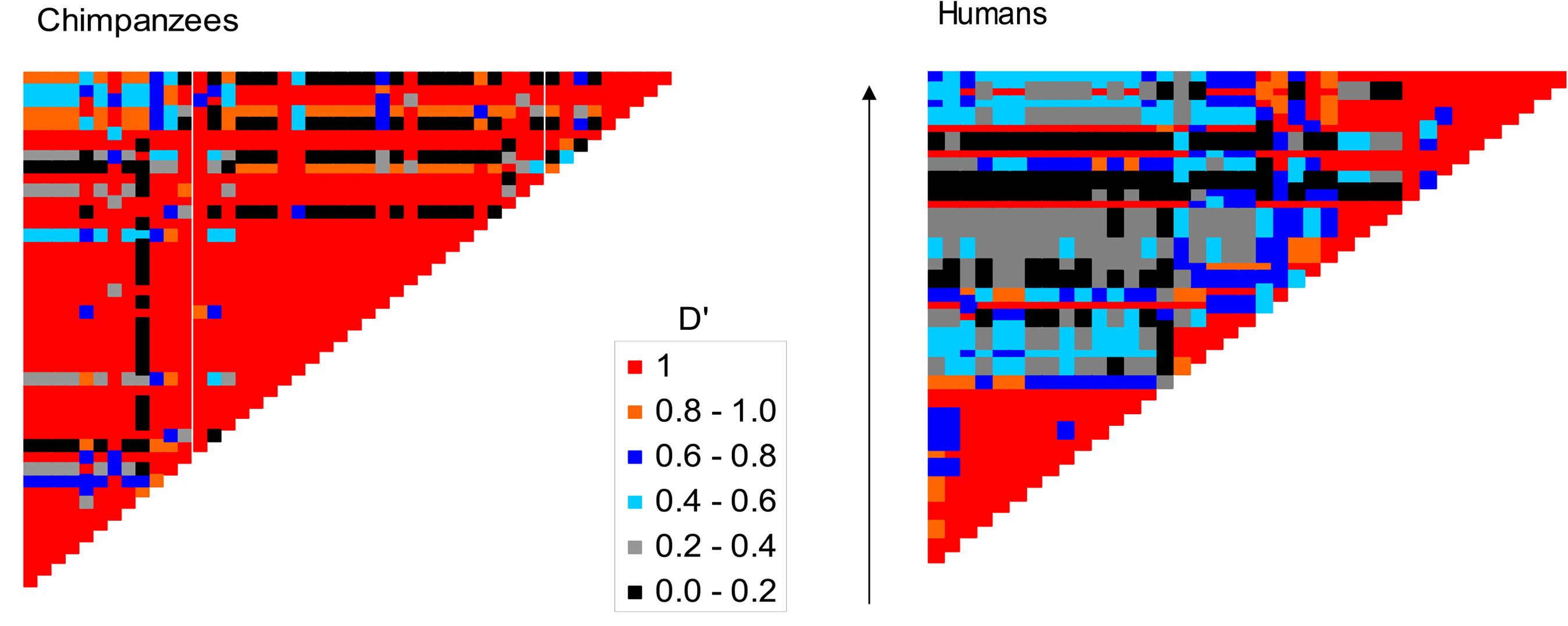
Nuestra estadística de desequilibrio de ligamiento\(D\) depende fuertemente de las frecuencias alélicas de los dos loci involucrados. Una forma común de eliminar parcialmente esta dependencia, y hacerla más comparable a través de loci, es\(D\) dividirla por su valor máximo posible dada la frecuencia de los loci. Esta estadística normalizada se llama\(D^{\prime}\) y varía entre\(+1\) y\(-1\). En la Figura\ ref {fig:TAPS_Hotspot} hay un ejemplo de LD a través de la región TAP2 en humanos y chimpancés. Observe cómo los SNP físicamente cercanos, es decir, los cercanos a la diagonal, tienen valores absolutos más altos,\(D^{\prime}\) ya que los alelos estrechamente vinculados se separan por recombinación con menos frecuencia permitiendo que se acumulen altos niveles de LD. A grandes distancias físicas, lejos de la diagonal, hay menor\(D^{\prime}\). Esto es especialmente notable en humanos ya que existe un punto de acceso intenso de recombinación específica humana en esta región, que está descomponiendo LD entre lados opuestos de esta región.
Otra estadística común para resumir LD es la\(r^2\) que escribimos como
\[r^2 = \frac{D^2}{p_A(1-p_A) p_B(1-p_B) }\]
Como\(D\) es una covarianza, y\(p_A(1-p_A)\) es la varianza de un alelo dibujado al azar a partir del locus\(A\),\(r^2\) es el coeficiente de correlación al cuadrado.
fracción.

La Figura\ ref {fig:Mouse_LD} muestra\(r^2\) para pares de SNP a diversas distancias físicas en dos muestras poblacionales de Mus musculus domesticus. Nuevamente, la LD es más alta entre marcadores físicamente cercanos ya que LD se genera más rápido de lo que puede descomponerse a través de la recombinación; los marcadores más distantes tienen LD mucho menor ya que aquí la recombinación está ganando. Tenga en cuenta que la descomposición de la LD es mucho más lenta en la población cruzada de generación adelantada que en la población natural capturada en la naturaleza. Esta persistencia de LD a través de megabases se debe al limitado número de generaciones para recombinación desde que se creó el cruce.

La generación de LD.
Diversas fuerzas genéticas poblacionales pueden generar LD. La selección puede generar LD favoreciendo combinaciones particulares de alelos. La deriva genética también generará LD, no porque se favorezcan combinaciones particulares de alelos, sino simplemente porque al azar los haplotipos particulares pueden derivar por casualidad en frecuencia. La mezcla entre poblaciones divergentes también puede generar LD, como vimos en la pregunta del ratón anterior.
La decadencia de LD por recombinación
Ahora examinaremos qué le sucede a la LD a lo largo de las generaciones si, en una población muy grande (es decir, ninguna deriva genética y las frecuencias de nuestros loci siguen así sus expectativas), solo permitimos que se produzca la recombinación. Para ello, considere la frecuencia de nuestro\(AB\) haplotipo en la próxima generación,\(p_{AB}^{\prime}\). Perdemos una fracción\(c\) de nuestros\(AB\) haplotipos por recombinación, separando nuestros alelos, pero ganamos una fracción\(cp_A p_B\) por generación de otros haplotipos que se recombinan juntos para formar\(AB\) haplotipos. Así, en la próxima generación
\[p_{AB}^{\prime} = (1-c)p_{AB} + cp_Ap_B \label{new_hap_freq}\]
El último término anterior, en\ ref {new_hap_freq}, se\(c(p_{AB}+p_{Ab})(p_{AB}+p_{aB})\) simplifica, que es la probabilidad de recombinación en los diferentes genotipos diploides que podrían generar un\(p_{AB}\) haplotipo.
Entonces podemos escribir el cambio en la frecuencia del\(p_{AB}\) haplotipo como
\[\Delta p_{AB} = p_{AB}^{\prime} -p_{AB} = -c p_{AB} + cp_Ap_B = - c D\]
[fig:ld_time]
[fig:ld_recom]
Por lo que la recombinación provocará una disminución en la frecuencia de\(p_{AB}\) si hay un exceso de\(AB\) haplotipos dentro de la población (\(D>0\)), y un aumento si hay un déficit de\(AB\) haplotipos dentro de la población ( \(D<0\)). Nuestro LD en la próxima generación es
\[\begin{aligned} D^{\prime} & = p_{AB}^{\prime} - p'_{A}p'_{B} \nonumber\\ & = (p_{AB} + \Delta p_{AB}) - (p_{A} + \Delta p_{A})(p_{B} + \Delta p_{B}) \nonumber\\ & = p_{AB} + \Delta p_{AB} - p_{A}p_{B} \nonumber\\ & = (1-c) D\end{aligned}\]
donde podemos cancelar\(\Delta p_{A}\) y\(\Delta p_{B}\) arriba porque la recombinación solo cambia haplotipo, no alelo, frecuencias. Entonces, si el nivel de LD en generación\(0\) es\(D_0\), el nivel\(t\) generaciones posteriores (\(D_t\)) es
\[D_t= (1-c)^t D_0\]
La recombinación está actuando para disminuir la LD, y lo hace geométricamente a una velocidad dada por\((1-c)\). Si\(c \ll 1\) entonces podemos aproximar esto por un exponencial y decir que
\[D_t \approx D_0 e^{-ct} \label{eqn_LD_decay}\]
que se desprende de una expansión de la serie Taylor, véase Apéndice\ ref {EQN:Taylor_geo}.
Se encuentra una población híbrida entre las dos subespecies de ratón descritas en la pregunta anterior, que parece estar compuesta por proporciones iguales (\(50/50\)) de ascendencia de las dos subespecies. Estimas LD entre los dos marcadores para ser\(D=0.0723\). Con base en trabajos previos se estima que los dos loci están separados por una fracción de recombinación de 0.1. Suponiendo que esta población híbrida es grande y estuvo formada por un solo evento de mezcla, ¿se puede estimar cuánto tiempo hace que se formó esta población?
Un ejemplo particularmente llamativo de la descomposición de la LD generada por la mezcla de poblaciones lo ofrece la LD creada por el mestizaje entre humanos y neandertales. Los neandertales y los humanos modernos divergieron entre sí probablemente hace más de medio millón de años, lo que permitió que las diferencias de frecuencia de los alelos se acumularan entre las poblaciones neandertales y humanas modernas. Las dos poblaciones volvieron a extenderse al contacto secundario cuando los humanos se mudaron fuera de África en los últimos cien mil años más o menos. Uno de los hallazgos más emocionantes de la secuenciación del genoma neandertal fue que las personas de hoy en día con ascendencia euroasiática llevan un pequeño porcentaje de su genoma derivado del genoma neandertal, a través del mestizaje durante este contacto secundario. Hasta la fecha, el momento de este mestizaje, se analizó el LD en humanos modernos entre pares de alelos encontrados derivados del genoma neandertal (y casi ausentes de las poblaciones africanas). En la Figura\ ref {fig:LD_Neanderthal} mostramos el LD promedio entre estos loci en función de la distancia genética (\(c\)) entre ellos, a partir del trabajo de.

Suponiendo una tasa de recombinación\(r\), podemos ajustar la decaimiento exponencial de LD predicho por\ ref {EQN_LD_Decay} a los puntos de datos en esta figura; el ajuste se muestra como una línea roja. Haciendo esto estimamos\(t=1200\) generaciones, o alrededor de 35 mil años (utilizando un tiempo de generación humana de 29 años). Así, el LD en los eurasiáticos modernos, entre alelos derivados del mestizaje con neandertales, representa más de treinta mil años de recombinación descomponiendo lentamente estas antiguas asociaciones.
Resumen
- Los individuos a menudo se aparean de forma no aleatoria, por ejemplo, por ubicación geográfica, esto genera una estructura genética poblacional que puede considerarse como una forma de endogamia. Esta endogamia a nivel poblacional conduce a una reducción en la heterocigosidad dentro de las subpoblaciones en comparación con la población total (si las frecuencias alélicas difieren entre las poblaciones).
- \(F\)Las estadísticas de Wright pueden ser utilizadas para medir el alcance de la estructura poblacional, describiendo la reducción de la heterocigosidad a diversas escalas, por ejemplo el individuo comparado con la subpoblación (\(F_{IS}\)) o la subpoblación en comparación con la población total ( \(F_{ST}\)). Podemos calcular estas estadísticas en todo el genoma o en loci individuales.
- Estas\(F\) estadísticas pueden entenderse como que expresan una correlación entre alelos extraídos del mismo nivel de estructura poblacional, o la proporción de varianza genética explicada por la estructura poblacional.
- Otras formas de visualizar la estructura poblacional incluyen enfoques similares a la estructura, que se basan en asignar individuos a poblaciones en función de la probabilidad de su genotipo dadas las frecuencias alélicas (métodos de asignación) y aprender la asignación de individuos a poblaciones discretas. Otro enfoque común se basa en la identificación de los principales ejes de variación en la relación a través del análisis de componentes principales.
- A menudo nos interesarán las covarianzas y correlaciones entre alelos en diferentes loci, desequilibrio de ligamiento (LD).
- La covarianza entre loci (LD) puede surgir entre loci por diversas razones, notablemente la estructura poblacional y la mezcla como se describe en el capítulo.
- La desintegración de LD debido a la recombinación puede modelarse y potencialmente usarse hasta la fecha cuando se generó LD (por ejemplo, mediante mezcla).
La pérdida de heterocigosidad debida a la endogamia se puede dividir a través de estadísticas F en múltiples niveles. Por ejemplo podemos dividir el coeficiente de endogamia total de un individuo (\(F_{IT}\)) comparado con una población entre\(F_{IS}\) y\(F_{ST}\). Para los siguientes escenarios de ejemplo, ¿espera\(F_{IS}\) ser más grande o menor que\(F_{ST}\)? Explica tu respuesta.
- Carlos II, donde la subpoblación es España y la población total son europeos.
- Subpoblaciones de plantas que viven en la ladera de una montaña, donde el polen se dispersa largas distancias a través del viento, pero los individuos se autopolinizan alrededor del 50% del tiempo,
- Peces que viven en lagos con muy pocas vías fluviales accesibles entre lagos, pero donde los peces nadan libremente dentro de los lagos. Cada lago es una subpoblación y toda la cuenca del lago es la población total.
En una especie de escarabajo, el color y la forma de las alas están controlados por dos polimorfismos distintos (con alelos grandes/pequeños y rojo/amarillo respectivamente). En una colección de museo se estima que la frecuencia de los cuatro haplotipos es:
| grande/rojo | grande/amarillo | pequeño/rojo | Pequeño/Amarillo |
| 0.69 | 0.00 | 0.09 | 0.22 |
Esta colección es de hace 60 años. En las poblaciones actuales se estima que las frecuencias de los haplotipos son:
| 0.5452 | 0.1448 | 0.2348 | 0.0752 |
- Asumiendo una generación por año, ¿cuál es la fracción de recombinación entre estos loci?
- Cualitativamente, ¿cómo cambiaría tu respuesta si determinaras que el cruce solo ocurrió en hembras y no en machos?


