2: Frecuencias de Alelos y Genotipos
- Page ID
- 58103
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En este capítulo trabajaremos a través de cómo se desarrollan los fundamentos de la genética mendeliana a nivel poblacional en organismos de reproducción sexual.
Los loci y los alelos son la moneda básica de la genética poblacional y, de hecho, de la genética. Un locus puede ser un gen completo, o un único par de bases nucleotídicas tal como A-T. En cada locus, puede haber múltiples variantes genéticas que se segregan en la población; estas diferentes variantes genéticas se conocen como alelos. Si todos los individuos de la población portan el mismo alelo, decimos que el locus es monomórfico; en este locus no hay variabilidad genética en la población. Si hay múltiples alelos en la población en un locus, decimos que este locus es polimórfico (esto a veces se denomina sitio segregante).
|
pos. |
con. |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
a |
b |
c |
d |
e |
f |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
NS/S |
||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
781 |
G |
T |
T |
T |
T |
T |
T |
T |
T |
T |
T |
T |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
NS |
||
|
789 |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
S |
||
|
808 |
A |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
G |
G |
G |
G |
G |
G |
G |
G |
G |
G |
G |
G |
NS |
||
|
816 |
G |
T |
T |
T |
T |
- |
- |
- |
- |
- |
- |
- |
T |
T |
T |
T |
T |
T |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
834 |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
C |
C |
- |
- |
- |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
859 |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
G |
G |
G |
G |
G |
G |
G |
G |
G |
G |
G |
G |
NS |
||
|
867 |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
G |
G |
G |
G |
G |
A |
G |
G |
G |
G |
G |
G |
S |
||
|
870 |
C |
T |
T |
T |
T |
T |
T |
T |
T |
T |
T |
T |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
950 |
G |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
974 |
G |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
T |
- |
T |
T |
T |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
983 |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
S |
||
|
1019 |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
1031 |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
- |
- |
- |
S |
||
|
1034 |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
C |
C |
C |
C |
C |
- |
- |
C |
- |
C |
C |
S |
|||
|
1043 |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
1068 |
C |
T |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
1089 |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
A |
A |
A |
A |
A |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
NS |
||
|
1101 |
G |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
NS |
||
|
1127 |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
S |
||
|
1131 |
C |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
T |
- |
- |
- |
- |
- |
- |
- |
S |
||
|
1160 |
T |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
S |
La Tabla\ ref {Tabla:ADH} muestra un pequeño tramo de secuencia ortóloga para el locus ADH de muestras de Drosophila melanogaster, D. simulans y D. yakuba. D. melanogaster y D. simulans son especies hermanas y D. yakuba es un grupo externo cercano a las dos. Cada columna representa un solo haplotipo de un individuo (los individuos son diploides pero eran endogámicos por lo que son homocigotos para su haplotipo). Solo se muestran sitios que difieren entre individuos de las tres especies. \(834\)El sitio es un ejemplo de polimorfismo; algunos individuos de D. simulans portan un\(C\) alelo mientras que otros tienen un\(T\). Las diferencias fijas son sitios que difieren entre las especies pero son monomórficos dentro de la especie. Sitio\(781\) es un ejemplo de una diferencia fija entre D. melanogaster y las otras dos especies.
También podemos anotar los alelos y loci de varias maneras. Por ejemplo, la posición\(781\) es una diferencia fija no sinónima. Llamamos al alelo menos común en un polimorfismo el alelo menor y al alelo común el alelo mayor, por ejemplo, en\(1068\) el sitio el\(T\) alelo es el alelo menor en D. melanogaster. Llamamos al más evolutivamente reciente de los dos alelos el alelo derivado y al más viejo de los dos el alelo ancestral. Inferimos que el\(T\) alelo en el sitio 1068 es el alelo derivado porque el\(C\) se encuentra en otras dos especies, lo que sugiere que el\(T\) alelo surgió a través de una\(C \rightarrow T\) mutación.
- ¿Cuántos sitios segregantes tiene la muestra de D. simulans en el gen ADH?
- ¿Cuántas diferencias fijas hay entre D. melanogaster y D. yakuba?
Frecuencias alélicas
Las frecuencias alélicas son una unidad central del análisis genético poblacional, pero a partir de individuos diploides solo podemos observar recuentos de genotipos. Nuestra primera tarea es entonces calcular frecuencias alélicas a partir de recuentos de genotipos. Considerar un locus autosómico diploide segregante para dos alelos (\(A_1\)y\(A_2\)). Utilizaremos estas etiquetas arbitrarias para nuestros alelos, simplemente para mantener este general. Dejar\(N_{11}\) y\(N_{12}\) ser el número de\(A_1A_1\) homocigotos y\(A_1A_2\) heterocigotos, respectivamente. Además, deja\(N\) ser el número total de individuos diploides en la población. Luego podemos definir las frecuencias relativas de\(A_1A_1\) y\(A_1A_2\) genotipos como\(f_{11} = N_{11}/N\) y\(f_{12} = N_{12}/N\), respectivamente. La frecuencia del alelo\(A_1\) en la población viene dada entonces por
\[p = \frac{2 N_{11} + N_{12}}{2N} = f_{11} + \frac{1}{2} f_{12}. \nonumber\]
Tenga en cuenta que esto se deriva directamente de cómo se cuentan los alelos dados los genotipos de individuos, y se mantiene independientemente de las proporciones y el equilibrio de Hardy-Weinberg (discutidos a continuación). La frecuencia del alelo alterno (\(A_2\)) es entonces justa\(q=1-p\).
Medidas de variabilidad genética
Diversidad de nucleótidos (\(\pi\)) - Una medida común de la diversidad genética es el número promedio de diferencias de un solo nucleótido entre haplotipos elegidos al azar de una muestra. Esto se llama diversidad de nucleótidos y a menudo se denota por\(\pi\). Por ejemplo, podemos calcular\(\pi\) para nuestro locus ADH a partir de la Tabla\ ref {tabla:ADH} anterior: tenemos 6 secuencias de D. simulans (a-f), hay un total de 15 formas de emparejar estas secuencias, y
\[\pi=\frac{1}{15} \big( (2 + 1 + 1 + 1 + 0 ) + (3 + 3 + 3 + 2 ) +(0 + 0 + 1) + (0 + 1) + (1) \big)=1.2\overline{6}\]
donde el primer término entre corchetes da las diferencias por pares entre a y b-f, el segundo término entre corchetes las diferencias entre b y c-f y así sucesivamente.
Nuestra\(\pi\) medida dependerá de la longitud de secuencia para la que se calcula. Por lo tanto, generalmente\(\pi\) se normaliza por la longitud de la secuencia, para ser una medida por sitio (o por base). Por ejemplo, nuestra secuencia de ADH cubre\(397\) pb de ADN y así\(\pi = 1.2\overline{6}/397=0.0032\) por sitio en D. simulans para esta región. Tenga en cuenta que también podríamos calcular\(\pi\) por sitio sinónimo (o no sinónimo). Para sitio sinónimo\(\pi\), contaríamos el número de diferencias sinónimas entre nuestros pares de secuencias, y luego dividiríamos por el número total de sitios donde podría haber ocurrido un cambio sinónimo. Técnicamente necesitaríamos dividir por el número total de posibles mutaciones puntuales que resultarían en un cambio sinónimo; esto se debe a que algunos cambios mutacionales en un nucleótido particular resultarán en un cambio no sinónimo o sinónimo dependiendo del cambio de pares de bases.
Número de sitios de segregación
Otra medida de variabilidad genética es el número total de sitios que son polimórficos (segregantes) en nuestra muestra. Un problema es que el número de sitios segregantes crecerá a medida que secuenciemos más individuos (a diferencia de\(\pi\)). Más adelante en el curso, hablaremos sobre cómo estandarizar el número de sitios segregantes para el número de individuos secuenciados (ver\ ref {watterson_theta}).
El espectro de frecuencia
También a menudo queremos recopilar información sobre la frecuencia de alelos en todos los sitios. Llamamos alelos que se encuentran una vez en una muestra singletones, alelos que se encuentran dos veces en una muestra dobletones, y así sucesivamente. Contamos el número de loci donde se encuentra un alelo\(i\) tiempos fuera de\(n\), por ejemplo, cuántos singletones hay en la muestra, y esto se llama espectro de frecuencia. Vamos a querer hacer esto de alguna manera consistente, como calcular el espectro de frecuencias del alelo menor o el alelo derivado.
¿Cuántos singletones de alelos menores hay en D. simulans en la región ADH? [Definir alelo menor justo dentro de D. simulans.]
Niveles de variabilidad genética entre especies
Dos observaciones han desconcertado a los genetistas poblacionales desde el inicio de la genética de poblaciones moleculares. El primero es el nivel relativamente alto de variación genética observado en las especies más obligadamente sexuales. Esta primera observación, en parte, impulsó el desarrollo de la teoría neutra de la evolución molecular, la idea de que gran parte de este polimorfismo molecular puede simplemente reflejar un equilibrio entre deriva genética y mutación. La segunda observación es el rango relativamente estrecho de polimorfismo entre especies con tamaños censales muy diferentes. Esta observación representó un rompecabezas ya que la teoría Neutral predice que los niveles de diversidad genética deben escalar con el tamaño de la población. Mucho esfuerzo en genética poblacional teórica y empírica se ha dedicado a tratar de conciliar modelos con estas diversas observaciones. Volveremos a discutir estas ideas a lo largo de nuestro curso.
Las primeras observaciones de la diversidad genética molecular dentro de las poblaciones naturales se realizaron a partir de encuestas de datos de alozima, pero podemos revisar estos patrones generales con datos modernos. Por ejemplo, Leffler et al. (2012) compilaron datos sobre los niveles de diversidad de nucleótidos autosómicos dentro de la población (π) para 167 especies en 14 filos de sitios no codificantes y sinónimos (Figura 2.3). La especie con los niveles más bajos de π en su encuesta fue Lynx, con π = 0.01%, es decir, solo 1/10000 bases difirieron entre dos secuencias. En contraste, algunos de los niveles más altos de diversidad se encontraron en Ciona savignyi, Sea Squirts, donde un notable 1/12 bases difieren entre pares de secuencias. Este rango de diversidad de 800 veces parece impresionante, pero los tamaños de la población censal tienen un rango mucho mayor.
Proporciones de Hardy-Weinberg
Imagínese que una población se aparea al azar con respecto a genotipos, es decir, sin endogamia, sin apareamiento selectivo, sin estructura poblacional y sin diferencias de sexo en las frecuencias alélicas. La frecuencia del alelo\(A_1\) en la población al momento de la reproducción es\(p\). Se elabora un\(A_1A_1\) genotipo al llegar a nuestra población y dibujar independientemente dos gametos\(A_1\) alélicos para formar un cigoto. Por lo tanto, la probabilidad de que un individuo sea\(A_1A_1\) homocigoto es\(p^2\). Esta probabilidad son también las frecuencias esperadas del\(A_1A_1\) homocigoto en la población. La frecuencia esperada de los tres genotipos posibles son
| \(f_{11}\) | \(f_{12}\) | \(f_{22}\) |
|---|---|---|
| \ (f_ {11}\)” style="text-align:center; ">\(p^2\) | \ (f_ {12}\)” style="text-align:center; ">\(2pq\) | \ (f_ {22}\)” style="text-align:center; ">\(q^2\) |
es decir, sus expectativas de Hardy-Weinberg. Tenga en cuenta que solo necesitamos asumir el apareamiento aleatorio con respecto a nuestro alelo focal para que estas frecuencias esperadas se mantengan en los cigotos que forman la siguiente generación. Las fuerzas evolutivas, como la selección, cambian las frecuencias alélicas dentro de generaciones, pero no cambian esta expectativa por nuevos cigotos, siempre y cuando\(p\) sea la frecuencia del\(A_1\) alelo en la población en el momento en que los gametos se fusionan. Solo necesitamos los supuestos de no migración, selección y mutación para que estas expectativas de Hardy-Weinberg de genotipos representen un equilibrio a largo plazo.
En las islas costeras de Columbia Británica hay una subespecie de oso negro (Ursus americanus kermodei, oso de Kermode). Muchos miembros de esta subespecie de oso negro son blancos; a veces se les llama osos espíritus. Estos osos no son híbridos con osos polares, ni son albinos. Son homocigotos para un cambio recesivo en el gen MC1R. Los individuos que están\(GG\) en este SNP son blancos, mientras que\(AA\) y\(AG\) los individuos son negros.
A continuación se presentan los recuentos de genotipos para el polimorfismo MC1R en una muestra de osos de poblaciones de islas de Columbia Británica de.
| \(AA\) | \(AG\) | \(GG\) |
|---|---|---|
| \ (AA\)” style="text-align:center; ">42 | \ (AG\)” style="text-align:center; ">24 | \ (GG\)” style="text-align:center; ">21 |
¿Cuáles son las frecuencias esperadas de los tres genotipos bajo HW?

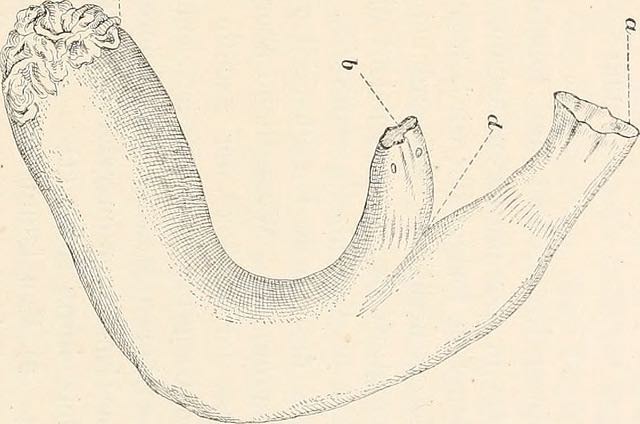
Ver Figura\ ref {fig:HWE_CEU_YRI} para una buena demostración empírica de las proporciones de Hardy-Weinberg. La frecuencia media de cada genotipo coincide estrechamente con sus expectativas de HW, y gran parte de la dispersión de los puntos alrededor de la línea esperada se debe a nuestro pequeño tamaño de muestra (\(\sim 60\)individuos). Si bien HW a menudo parece un modelo tonto, a menudo se mantiene notablemente bien dentro de las poblaciones. Esto se debe a que los individuos no se aparean al azar, sino que se aparean al azar con respecto a su genotipo en la mayoría de los loci del genoma.
Se está investigando un locus con tres alelos, A, B y C, con frecuencias alélicas\(p_A\),\(p_B\), y\(p_C\). ¿Qué fracción de la población se espera que sean homocigotos bajo Hardy-Weinberg?
Los microsatélites son regiones del genoma donde los individuos varían por el número de copias de alguna repetición corta de ADN que llevan. Estas regiones suelen ser muy variables entre individuos, lo que las convierte en una forma adecuada de identificar individuos a partir de una muestra de ADN. Esta llamada huella digital de ADN tiene una gama de aplicaciones desde establecer la paternidad e identificar restos humanos hasta emparejar individuos con muestras de ADN de la escena del crimen. El FBI hace uso de la base de datos del CODIS. La base de datos del CODIS contiene los genotipos de más de 13 millones de personas, la mayoría de las cuales han sido condenadas por un delito. La mayoría de los perfiles registran genotipos en 13 loci de microsatélites que son repeticiones de tetranucleótidos (desde 2017, se han genotipado 20 sitios).
Los recuentos de alelos para dos loci (D16S539 y TH01) se muestran en la tabla\ ref {table:codis_1} y\ ref {table:codis_2} para una muestra de 155 personas de ascendencia europea. Se puede suponer que estos dos loci están en diferentes cromosomas.
[tabla: CODIS _1]
[tabla: CODIS _2]
Se extrae una muestra de ADN de la escena de un crimen. El genotipo es 100/80 en el locus D16S539 y 70/93 en TH01.
- Tienes a un sospechoso bajo custodia. Suponiendo que este sospechoso es inocente y de ascendencia europea, ¿cuál es la probabilidad de que su genotipo coincida con este perfil por casualidad (una probabilidad de coincidencia falsa)?
- El FBI utiliza\(\geq\) 13 marcadores. ¿Por qué es necesario este número mayor para que la declaración del partido sea prueba convincente en la corte?
- Un caso temprano que desencadenó el debate entre genetistas forenses fue un crimen entre los Abenaki, una comunidad nativa americana en Vermont. Había una muestra de ADN de la escena del crimen, y se pensó que el perpetrador probablemente era miembro de la comunidad Abenaki. Dado que las frecuencias alélicas varían entre las poblaciones, ¿por qué las personas estarían preocupadas por usar datos de una población no abenaki para calcular una probabilidad de coincidencia falsa?
Apareamiento surtido
Una violación importante de los supuestos de Hardy Weinberg es el apareamiento no aleatorio con respecto al genotipo en un locus. Una forma en que los individuos pueden aparearse de forma no aleatoria es si los individuos eligen aparearse basándose en un fenotipo determinado (en parte) por el genotipo en un locus. Este apareamiento no aleatorio puede ser entre: 1) individuos con fenotipo similar, el llamado apareamiento selectivo positivo o 2) individuos con fenotipos diferentes, apareamiento selectivo negativo o apareamiento desordenado. Aquí discutiremos brevemente un par de ejemplos reales de apareamiento surtido para asegurarnos de que todos estamos en la misma página. Encontraremos otras formas de apareamiento no aleatorio, debido a la endogamia y la estructura poblacional, en los próximos capítulos.
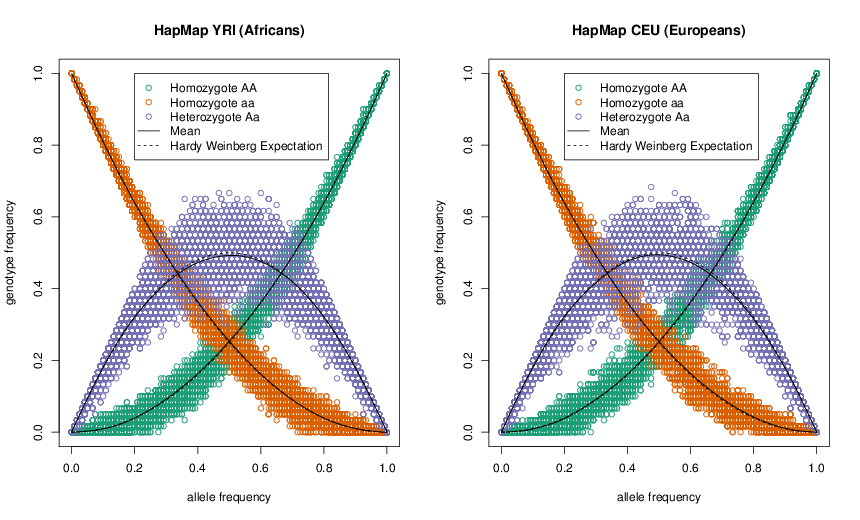
El apareamiento selectivo positivo sobre la base de un fenotipo puede crear un exceso de homocigotos. Las mariposas Heliconius son famosas por su mimetismo, donde pares venenosos de especies distantemente relacionadas imitan los patrones de colores brillantes de los demás y así comparten los beneficios de ser evitados por los depredadores visuales (imitadores müllerianos). H. melpomene rosina y H. cydno chioneus son especies estrechamente relacionadas que coexisten en el centro de Panamá, pero imitan a otras especies concurrentes diferentes (Figura\ ref {fig:Heliconius_Merrill_Assort}). Estas diferencias en el patrón de coloración se deben a unos pocos loci con grandes efectos fenotípicos. Las dos especies pueden hibridarse y producir híbridos F1 viables. Estos híbridos F1 son heterocigotos en los loci de color, y su apariencia intermedia significa que son imitadores pobres y, por lo tanto, son devorados rápidamente por los depredadores. Sin embargo, estos híbridos heterocigotos (F1) son muy raros en la naturaleza\(< \frac{1}{1000}\), ya que las especies parentales muestran un fuerte apareamiento selectivo positivo basado en el patrón de color, basado en diferencias genéticas en la preferencia de pareja.


El apareamiento desagrupado, apareamiento de individuos diferentes, puede conducir a un exceso de heterocigotos y un déficit de homocigotos. Un ejemplo de apareamiento dessurtido muy fuerte lo ofrecen los gorriones de garganta blanca (Zonotrichia albicollis). En los gorriones de garganta blanca, hay una morfa de rayas blancas y una de rayas bronceadas, con morfos hembra y macho de rayas blancas tienen una franja blanca y garganta mucho más brillantes. Hay un apareamiento desordenado muy fuerte en este sistema, con 1099 de 1116 parejas anidadas que consisten en una morfa de rayas marrones y una de rayas blancas y solo 17 de estas parejas de anidación son diferentes morfos. La diferencia entre estos morfos tiene un patrón de herencia simple, siendo el blanco debido a un solo alelo dominante (llamado 2m) y color bronceado de un alelo recesivo llamado 2. Así, un fuerte apareamiento desordenativo tiene un fuerte efecto sobre las frecuencias del genotipo:
| Broncea | Blanco | (Super) Blanco |
|---|---|---|
| 2/2 | 2/2m | 2m/2m |
| 978 | 1011 | 3 |
Casi no hay homocigotos de 2m (los llamados individuos Super blancos) a pesar de que el alelo de 2m es común en la población (datos de Tuttle et al., 2016, tabla S1).
Otro ejemplo importante de apareamiento desagrupado son los sistemas de tipo apareamiento, que están presentes en muchos hongos, algas y protozoos. Los gametos de la misma especie solo pueden fusionarse para formar un cigoto si difieren en el tipo de apareamiento. El tipo de apareamiento de gametos está controlado genéticamente por un locus de tipo apareamiento, por lo que los individuos son casi siempre heterocigotos en este locus. En algunos grupos de organismos, solo hay dos alelos diferentes, en otros clados estos loci tienen decenas o cientos de alelos.

En una colección de 18 cuerpos fructíferos de una población de Sparassis, todos los individuos eran heterocigotos para el tipo de apareamiento y se identificaron genéticamente 17 tipos de apareamiento diferentes (James, 2015; Martin y Gilbertson, 1978). (CC BY-SA 3.0; CC BY 3.0 vía Wikipedia)
Compartir alelos entre individuos relacionados e Identidad por Descenso
Todos los individuos de una población están relacionados entre sí por un pedigrí gigante (árbol genealógico). Para la mayoría de las parejas de individuos en una población estas relaciones son muy distantes (por ejemplo, primos lejanos), mientras que algunos individuos estarán más estrechamente relacionados (por ejemplo, hermanos/primos hermanos). Todos los individuos están relacionados entre sí por diferentes niveles de parentesco o parentesco. Los individuos relacionados pueden compartir alelos que han descendido ambos del ancestro común compartido. Para ser compartidos, estos alelos deben heredarse a través de todas las meiosis que conectan a los dos individuos (por ejemplo, sobrevivir a la\(\frac{1}{2}\) probabilidad de segregación de cada meiosis). A medida que los parientes más cercanos están separados por menos meiosis, los parientes más cercanos comparten más alelos. En la Figura\ ref {fig:ibd_cousins_chr_cartoon} mostramos el intercambio de regiones cromosómicas entre dos primos. Como veremos, muchos conceptos genéticos poblacionales y cuantitativos se basan en lo estrechamente relacionados que están los individuos, y por lo tanto necesitamos alguna manera de cuantificar el grado de parentesco entre los individuos.
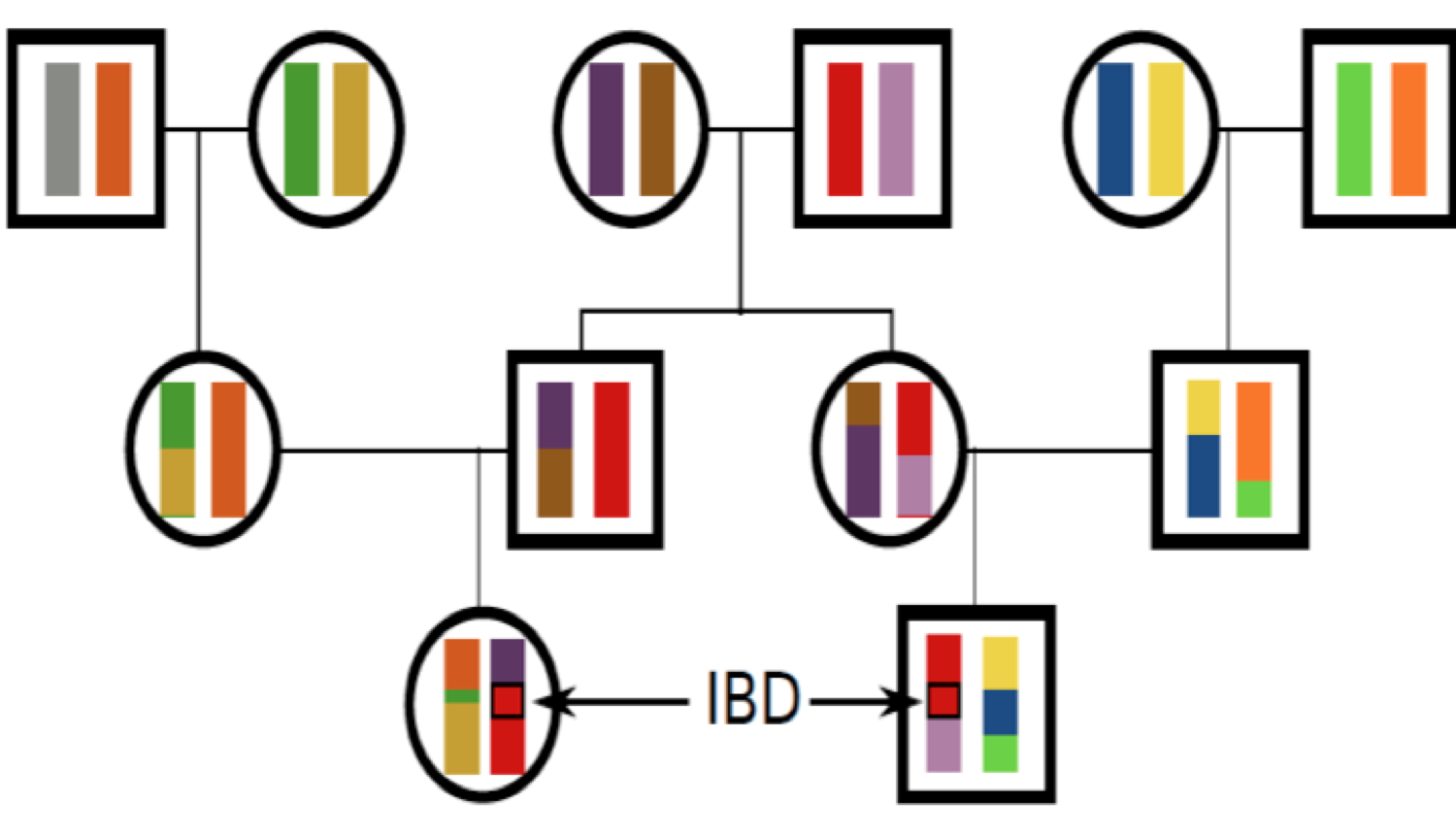
Definiremos dos alelos para que sean idénticos por descendencia (EII) si son idénticos debido a la transmisión de un ancestro común en las últimas generaciones. Por el momento, ignoramos la mutación, y seremos más precisos sobre lo que queremos decir con 'generaciones pasadas' más adelante. Por ejemplo, padre e hijo comparten exactamente un alelo idéntico por descendencia en un locus, asumiendo que los dos padres del niño son individuos apareados aleatoriamente de la población. En la Figura\ ref {fig:IBD_Cousins_cartoon}, muestro un pedigrí que demuestra algunas configuraciones de EII.
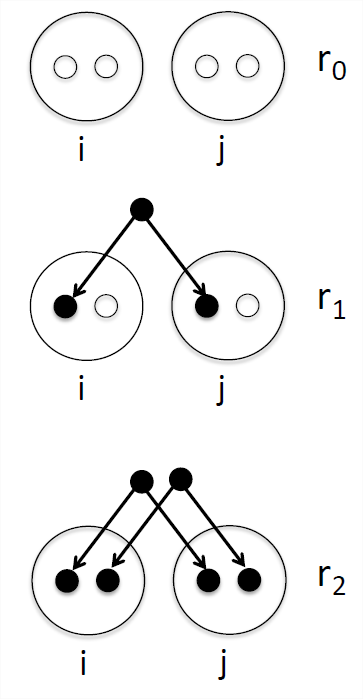
Un resumen de cuán relacionados están dos individuos (llamémoslos\(i\) y\(j\)) es la probabilidad de que nuestro par de individuos comparta 0, 1 o 2 alelos idénticos por descendencia (ver Figura\ ref {Fig:IBD_0_1_2}). Denotamos estas probabilidades de identidad por descendencia por\(r_0\)\(r_1\), y\(r_2\) respectivamente. Ver Tabla\ ref {tabla:IBDProbs} para algunos ejemplos. También podemos interpretar estas probabilidades como promedios de todo el genoma. Por ejemplo, en promedio, en una cuarta parte de todos sus loci autosómicos los hermanos completos comparten cero alelos idénticos por descenso.
Un resumen de la relación que será importante es la probabilidad de que dos alelos (I & J) escogieran al azar, uno de cada uno de los dos individuos diferentes\(i\) y\(j\), sean idénticos por descendencia (\(P(\text{i & j IBD})\)). Llamamos a esta cantidad el coeficiente de parentesco de los individuos\(i\) y\(j\), y la denotamos por\(F_{ij}\). Se calcula como
\[\begin{aligned} F_{ij} = & \mathbb{P}(\text{I & J IBD} )\\[4pt] =& \mathbb{P}(\text{I & J IBD} |~ \text{i & j 0 IBD}) \mathbb{P}(\text{i & j 0 IBD}) + \mathbb{P}(\text{I & J IBD} |~ \text{i & j 1 IBD}) \mathbb{P}(\text{i & j 1 IBD}) + \mathbb{P}(\text{I & J IBD} |~ \text{i & j 2 IBD}) \mathbb{P}(\text{i & j 2 IBD}) \label{eqn:coeffkinship_step}\\[4pt] = & 0 \times r_0 + \frac{1}{4} r_1 + \frac{1}{2} r_2. \label{eqn:coeffkinship}\end{aligned}\]
En el paso anterior,\ ref {eqn:coeffkinship_step}, estamos sumando la probabilidad condicional de que los alelos\(I\) y\(J\) sean EII sobre si nuestros individuos\(i\) &\(j\) comparten\(0\),\(1\), o \(2\)alelos EII, un ejemplo de uso de la Ley de Probabilidad Total (ver Apéndice\ ref {eqn:law_tot_prob}). Entonces, en\ ref {eqn:coeffkinship}, hemos usado el hecho de que podemos calcular nuestras probabilidades de condición de que I & J sea EII usando las reglas de la transmisión mendeliana. Considere la probabilidad\(P(\text{i & j IBD} |~ \text{i & j 1 IBD})\), es decir, que nuestro par de alelos (\(I\)&\(J\)) extraídos de individuos\(i\) y\(j\) son IBD dado que\(i\) y\(j\) comparten un alelo EII, esto es un\(\frac{1}{4}\) ya que necesitamos dibujar el alelo que es EII de ambos\(i\) y\(j\), es decir, dibujar ambos alelos negros en el panel medio de la Figura\ ref {fig:IBD_0_1_2}, lo que ocurre con probabilidad\(\frac{1}{2} \times \frac{1}{2}\). El coeficiente de parentesco aparecerá múltiples veces, tanto en nuestra discusión sobre la endogamia como en el contexto del parecido fenotípico entre parientes.
| Relación (i, j)\(^{*}\) | \(\mathbb{P}(\text{i & j 0 IBD})\) | \(\mathbb{P}(\text{i & j 1 IBD})\) | \(P(\text{i & j 2 IBD})\) | \(\mathbb{P}(\text{i & j IBD} )\) |
|---|---|---|---|---|
| \ (^ {*}\)” style="text-align:left; ">Relación (i, j)\(^{*}\) | \ (\ mathbb {P} (\ text {i & j 0 IBD})\)” style="text-align:center; ">\(r_0\) | \ (\ mathbb {P} (\ text {i & j 1 IBD})\)” style="text-align:center; ">\(r_1\) | \ (P (\ text {i & j 2 IBD})\)” style="text-align:center; ">\(r_2\) | \ (\ mathbb {P} (\ text {i & j IBD})\)” style="text-align:center; ">\(F_{ij}\) |
| \ (^ {*}\)” style="text-align:left; ">parent—child | \ (\ mathbb {P} (\ text {i & j 0 IBD})\)” style="text-align:center; ">0 | \ (\ mathbb {P} (\ text {i & j 1 IBD})\)” style="text-align:center; ">1 | \ (P (\ text {i & j 2 IBD})\)” style="text-align:center; ">0 | \ (\ mathbb {P} (\ text {i & j IBD})\)” style="text-align:center; "> |
| \ (^ {*}\)” style="text-align:left; ">hermanos completos | \ (\ mathbb {P} (\ text {i & j 0 IBD})\)” style="text-align:center; "> | \ (\ mathbb {P} (\ text {i & j 1 IBD})\)” style="text-align:center; "> | \ (P (\ text {i & j 2 IBD})\)” style="text-align:center; "> | \ (\ mathbb {P} (\ text {i & j IBD})\)” style="text-align:center; "> |
| \ (^ {*}\)” style="text-align:left; ">Gemelos monocigóticos | \ (\ mathbb {P} (\ text {i & j 0 IBD})\)” style="text-align:center; ">0 | \ (\ mathbb {P} (\ text {i & j 1 IBD})\)” style="text-align:center; ">0 | \ (P (\ text {i & j 2 IBD})\)” style="text-align:center; ">1 | \ (\ mathbb {P} (\ text {i & j IBD})\)” style="text-align:center; "> |
| \ (^ {*}\)” style="text-align:left; ">\(1^{st}\) primos | \ (\ mathbb {P} (\ text {i & j 0 IBD})\)” style="text-align:center; "> | \ (\ mathbb {P} (\ text {i & j 1 IBD})\)” style="text-align:center; "> | \ (P (\ text {i & j 2 IBD})\)” style="text-align:center; ">0 | \ (\ mathbb {P} (\ text {i & j IBD})\)” style="text-align:center; "> |
¿Qué son\(r_0\)\(r_1\), y\(r_2\) para los\(\frac{1}{2}\) hermanos? (los\(\frac{1}{2}\) sibs comparten uno de los padres pero no el otro).
Explique en palabras por qué\(\mathbb{P}(\text{i & j IBD} |~ \text{i & j 2 IBD}) = \frac{1}{2}\).
Compartición genotípica entre parejas de individuos
Nuestros\(r\) coeficientes van a tener diversos usos. Por ejemplo, nos permiten calcular la probabilidad de los genotipos de un par de parientes. Considere un locus bialélico donde el alelo\(A_1\) está en frecuencia\(p\), y dos individuos que tienen alelo IBD comparten probabilidades\(r_0\),\(r_1\),\(r_2\). ¿Cuál es la probabilidad general de que estos dos individuos sean homocigotos para el alelo 1? Bueno, eso es
\[\begin{aligned} \mathbb{P}(\textrm{both } A_1 A_1) = & \mathbb{P}(\textrm{both } A_1 A_1 | 0 \text{ alleles } \mathrm{IBD}) \mathbb{P}(0 \text{ alleles } \mathrm{IBD}) + \mathbb{P}(\textrm{both } A_1 A_1 | 1 \text{ allele }IBD) \mathbb{P}(1\text{ allele }IBD) + \mathbb{P}(\textrm{both } A_1 A_1 | 2 \text{ alleles }IBD) \mathbb{P}(2\text{ alleles }IBD)\end{aligned}\]
O, en nuestra\(r_0\),\(r_1\),\(r_2\) notación:
\[\begin{aligned} \mathbb{P}(\textrm{both } A_1 A_1) = & \mathbb{P}(\textrm{both } A_1 A_1 | \textrm{0 alleles IBD}) r_0 + \mathbb{P}(\textrm{both } A_1 A_1 | \textrm{1 alleles IBD}) r_1 + \mathbb{P}(\textrm{both } A_1 A_1 | \textrm{2 alleles IBD}) r_2 \label{eqn:initial_relly_IBD_calc}\end{aligned}\]
Si nuestro par de familiares comparten\(0\) alelos EII, entonces la probabilidad de que ambos sean homocigotos es\(\mathbb{P}(\textrm{both } A_1 A_1 | \text{0 alleles IBD}) =p^2 \times p^2\), ya que los cuatro alelos representan sorteos independientes de la población. Si comparten EII\(1\) alélico, entonces el alelo compartido es de tipo\(A_1\) con probabilidad\(p\), y luego el otro alelo no IBD, en ambos parientes, también necesita ser\(A_1\) lo que sucede con probabilidad\(p^2\), entonces \(\mathbb{P}(\textrm{both } A_1 A_1 | \text{1 alleles IBD})=p \times p^2\). Por último, nuestro par de familiares puede compartir dos alelos IBD, en cuyo caso\(\mathbb{P}(\textrm{both } A_1 A_1 | \text{2 alleles IBD}) = p^2\), porque si uno de nuestros individuos es homocigoto para el\(A_1\) alelo, ambos individuos lo serán. Armando todo esto nuestro\ ref {eqn:initial_relly_ibd_calc} se convierte en
\[\mathbb{P}(\textrm{both } A_1 A_1) = p^4 r_0 + p^3 r_1 + p^2 r_2 \label{eqn:IBD_relly_calc}\]
Tenga en cuenta que para casos específicos también podríamos calcular esto sumando todos los genotipos posibles que tenían sus ancestros compartidos; sin embargo, eso estaría mucho más involucrado y no tan general como la forma que aquí hemos derivado.
Podemos escribir términos como\ ref {eqn:ibd_relly_calc} para todas las configuraciones posibles de compartición/no compartición de genotipo entre un par de individuos. Con base en esto podemos anotar el número esperado de sitios polimórficos donde se observa que nuestros individuos comparten 0, 1 o 2 alelos.
El genotipo de nuestro sospechoso en Pregunta\ ref {Q:CODIS} resulta ser 100/80 para D16S539 y 70/80 en TH01. El sospechoso no coincide con el ADN de la escena del crimen; sin embargo, podrían ser hermanos.Calcular la probabilidad conjunta de observar el genotipo del crimen y nuestro sospechoso:
- Asumiendo que no comparten ninguna relación cercana.
- Asumiendo que son hermanos llenos.
- Explique brevemente sus hallazgos.
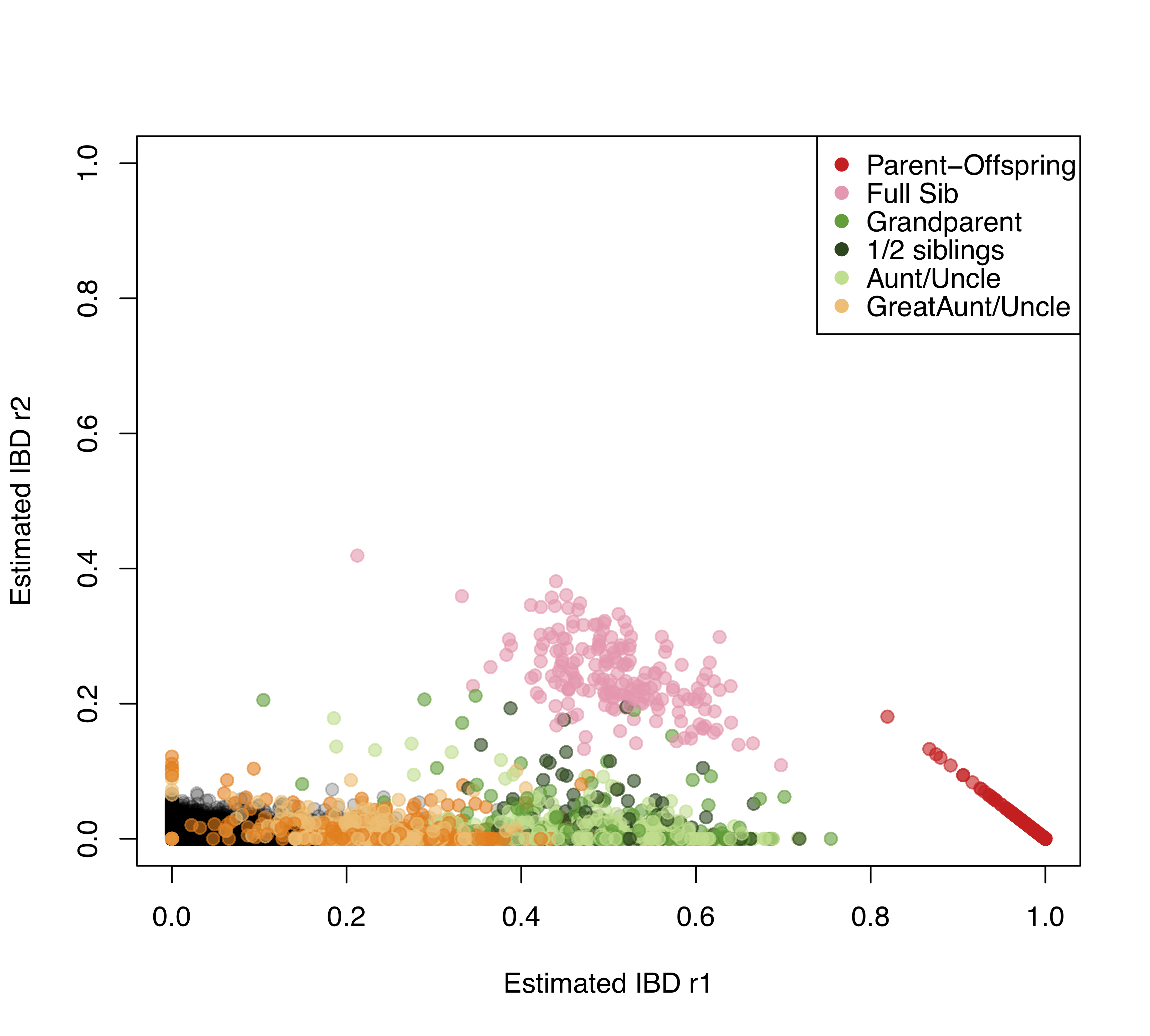
Hay una variedad de formas de estimar las relaciones entre individuos usando datos genéticos. Un ejemplo de uso compartido de alelos para identificar a familiares lo ofrece el trabajo de Nancy Chen. Ha recopilado datos de genotipado de miles de Florida Scrub Jays en más de diez mil loci. Estos arrendajos viven en el sitio de campo Archbold, y han sido monitoreados cuidadosamente durante muchas décadas permitiendo que se conozca el pedigrí de muchas de las aves. Con estos datos, estima frecuencias alélicas en cada locus. Luego, al equiparar el número observado de veces que un par de individuos comparten\(0\)\(1\), o\(2\) alelos con la expectativa teórica, estima la probabilidad de\(r_0\)\(r_1\), y\(r_2\) para cada par de aves. Una gráfica de estos se muestra en la Figura\ ref {fig:FSJ_IBD}, mostrando qué tan bien coinciden las estimaciones con las conocidas del pedigrí.
Intercambio de bloques genómicos entre familiares
Podemos ver más directamente el intercambio del genoma entre parientes cercanos utilizando matrices de genotipado de SNP de alta densidad. En la Figura\ ref {fig:First_cousin_IBD} mostramos una simulación del intercambio genómico de primos hermanos de su abuela compartida. De color púrpura son regiones donde tienen material genómico coincidente, debido a haberla heredado EII de su abuela compartida.
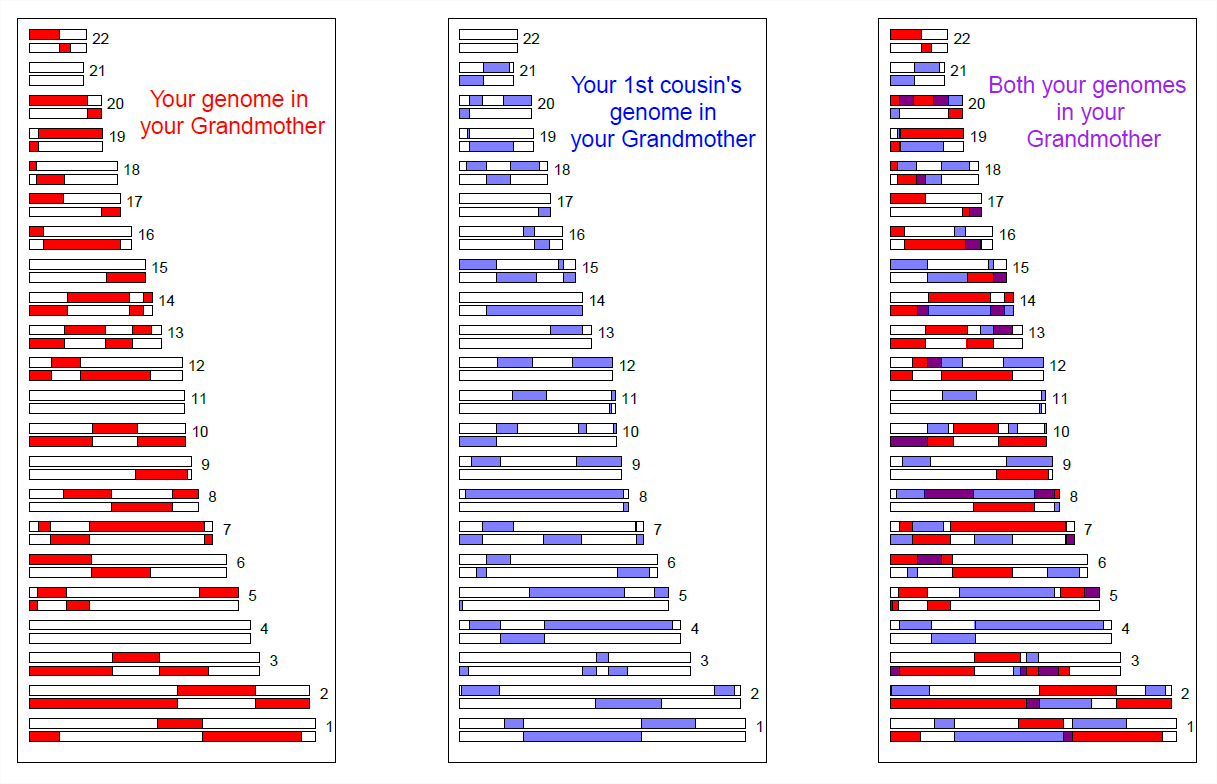
Los primos hermanos compartirán al menos un alelo de su genotipo en todos los loci polimórficos en estas regiones moradas. Hay una variedad de métodos para detectar tal intercambio. Una forma es buscar tramos inusualmente largos del genoma donde dos individuos nunca sean homocigotos para diferentes alelos. Al identificar parejas de individuos que comparten un número inusualmente grande de dichos supuestos bloqueos de EII, podemos esperar identificar parientes desconocidos en conjuntos de datos de genotipado. De hecho, empresas como 23&me y Ancestry.com utilizan señales de EII para ayudar a identificar lazos familiares.
Como otro ejemplo, consideremos el caso de primos terceros. Compartes uno de los ocho grupos de tatarabuelos con cada uno de tus (probablemente muchos) primos terceros. En promedio, tú y cada uno de tus primos terceros heredan cada uno una decimosexta parte de tu genoma de cada uno de esos dos tatarabuelos. Esto resulta implicar que en promedio, un poco menos del uno por ciento de los genomas tuyo y el de tu primo tercero (\(2 \times (1/16)^2 =0.78\%\)) serán idénticos en virtud de la descendencia de esos antepasados compartidos. Un ejemplo simulado donde primos terceros comparten bloques de su genoma (en los cromosomas 16 y 2) debido a su tatarabuela se muestra en la Figura\ ref {fig:third_cousin_IBD}.
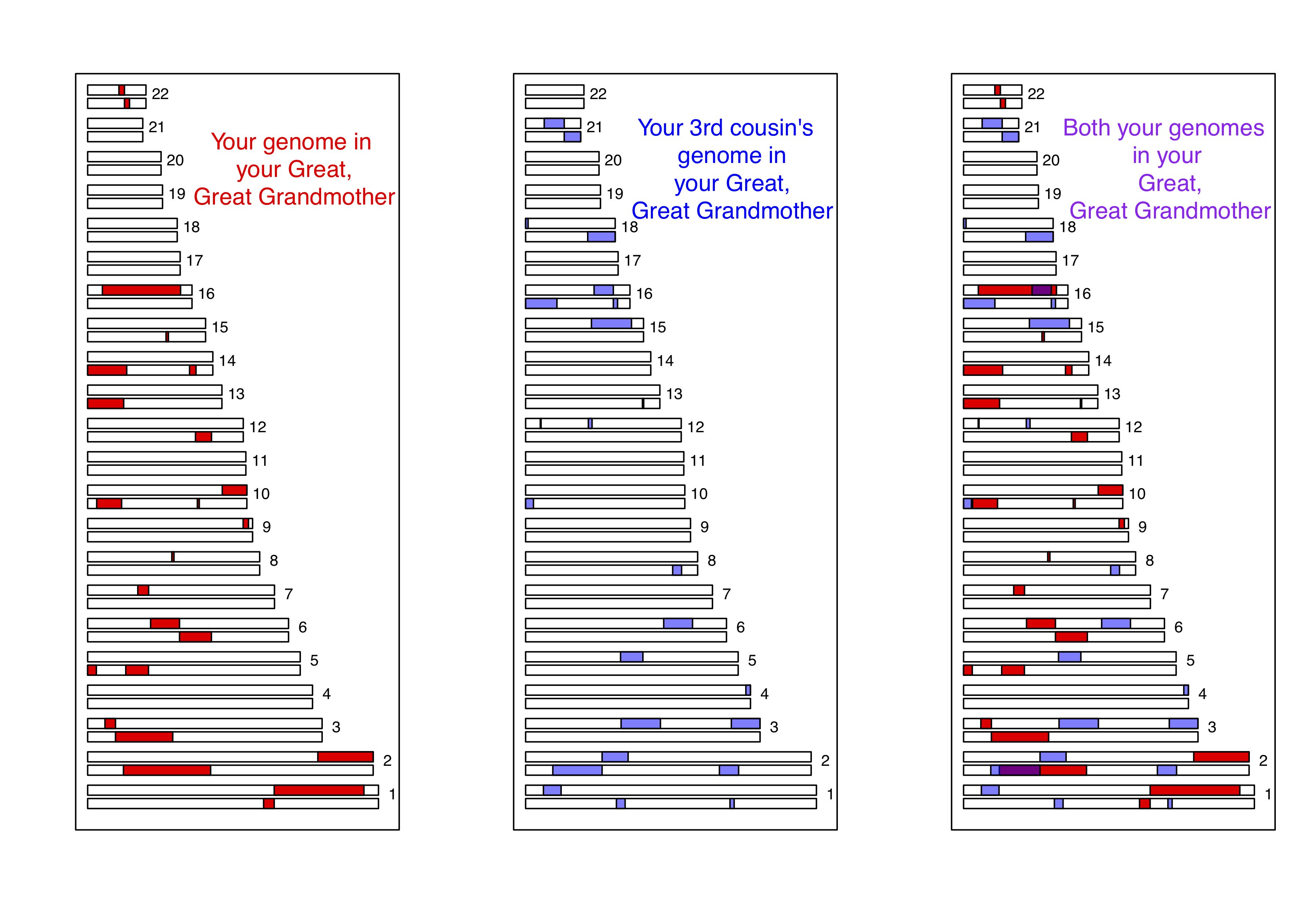
Observe cómo si compara la Figura\ ref {fig:third_cousin_IBD} y la Figura\ ref {fig:First_cousin_IBD}, los individuos heredan menos EII de una tatarabuela compartida que de una abuela compartida, ya que heredan de ancestros más totales más atrás. También observe cómo el intercambio ocurre en bloques genómicos más cortos, ya que ha pasado por más generaciones de recombinación durante la meiosis. Estos bloques aún son detectables, por lo que los primos terceros pueden detectarse usando chips de genotipado de alta densidad, lo que permite identificar a parientes más distantes que los métodos de un solo marcador por sí solos. Las relaciones más distantes que los primos terceros, por ejemplo, primos cuartos, comienzan a tener una probabilidad significativa de no compartir ninguna de sus EII genómicas. Pero tienes muchos primos cuartos, por lo que compartirás parte de tu EII del genoma con algunos de ellos; sin embargo, cada vez es más difícil identificar el grado de parentesco a partir de datos genéticos cuanto más profundo en el árbol genealógico va este intercambio.
Endogamia
Podemos definir a un individuo endogámico como un individuo cuyos padres están más estrechamente relacionados entre sí que dos individuos aleatorios extraídos de alguna población de referencia.
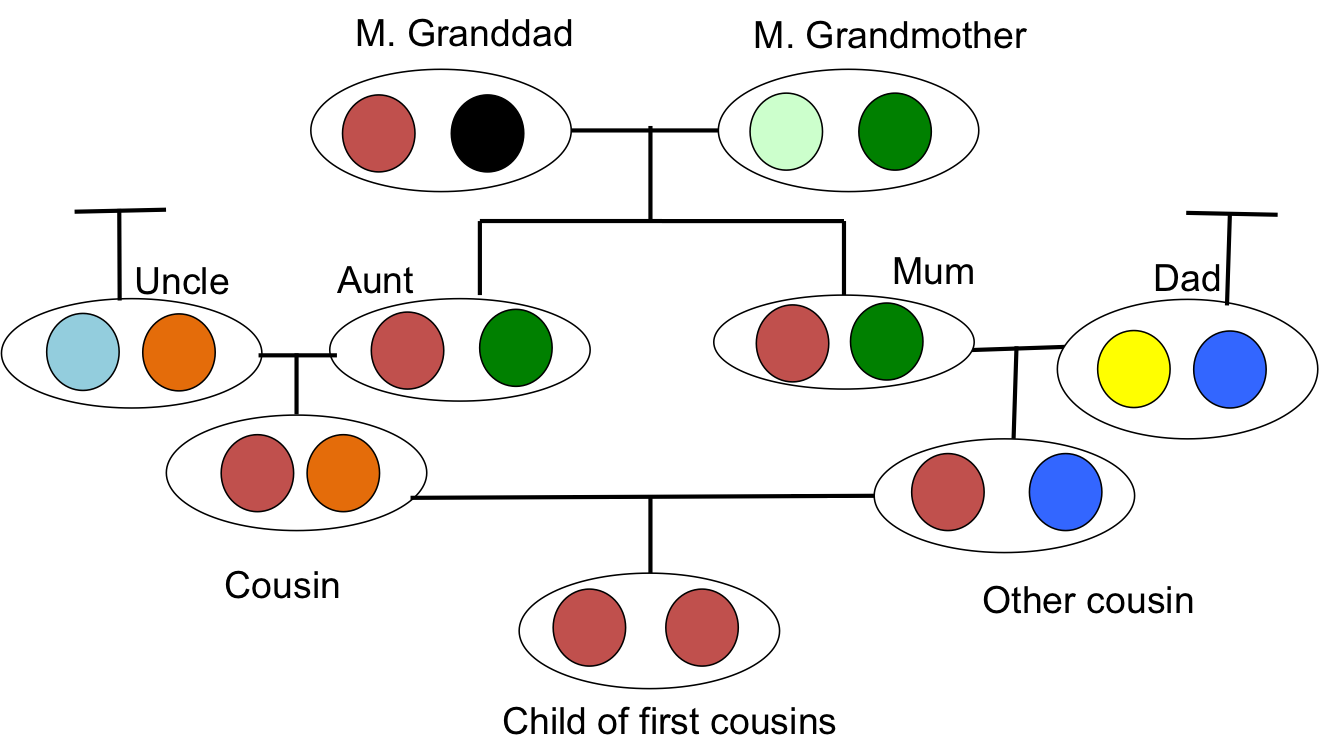
Cuando dos individuos relacionados producen una descendencia, ese individuo puede recibir dos alelos que son idénticos por descendencia, es decir, pueden ser homocigotos por descendencia (a veces denominados autozigotos), debido a que tienen dos copias de un alelo a través de diferentes caminos a través del pedigrí. Esta mayor probabilidad de ser homocigótico en relación con un individuo exogamia es el efecto más obvio de la endogamia. También es la que más nos interesará, ya que subyace a muchas de nuestras ideas sobre la depresión endogámica y la estructura poblacional. Por ejemplo, en la Figura\ ref {fig:IBD_Cousins_cartoon} nuestra descendencia de primos hermanos es homocigótica por descenso habiendo recibido el mismo alelo IBD a través de dos rutas diferentes alrededor de un bucle de endogamia.
A medida que la descendencia recibe un alelo aleatorio de cada padre (\(i\)y\(j\)), la probabilidad de que esos dos alelos sean idénticos por descendencia es igual al coeficiente\(F_{ij}\) de parentesco de los dos padres (\ ref {eqn:coeffkinship}). Esto se deduce de que el genotipo de la descendencia se realiza muestreando un alelo al azar de cada uno de nuestros padres.
| \(f_{11}\) | \(f_{12}\) | \(f_{22}\) |
|---|---|---|
| \ (f_ {11}\)” style="text-align:center; ">\((1-F) p^2 + F p\) | \ (f_ {12}\)” style="text-align:center; ">\((1-F) 2pq\) | \ (f_ {22}\)” style="text-align:center; ">\((1-F) q^2 + F q\) |
La única forma en que la descendencia puede ser heterocigótica (\(A_1 A_2\)) es si sus dos alelos en un locus no son EII (de lo contrario necesariamente serían homocigotos). Por lo tanto, la probabilidad de que sean heterocigotos es
\[\mathbb{P}(A_1 A_2) = \mathbb{P}(A_1 A_2 |\textrm{I & J not IBD} ) \P (\textrm{I & J not IBD} ) = 2p q (1-F_{ij}) , \label{eq:hetGenHW}\]
La descendencia puede ser homocigótica para el\(A_1\) alelo de dos maneras diferentes. Pueden tener dos alelos no IBD que no son EII pero resultan ser de tipo alélico\(A_1\), o sus dos alelos pueden ser IBD, de tal manera que heredaron el alelo\(A_1\) por dos vías distintas del mismo antepasado. Así, la probabilidad de que una descendencia sea homocigótica para\(A_1\) es
\[\begin{aligned} P(A_1 A_1) & = \mathbb{P}(A_1 A_1 |\textrm{I & J not IBD} ) \P (\textrm{i & j not IBD} ) + \mathbb{P}(A_1 A_1 |\textrm{i & j IBD} ) \P (\textrm{i & j IBD}) \nonumber\\ &= p^2(1-F_{ij}) + pF_{ij}.\end{aligned}\]
usando la Ley de Probabilidad Total (ver Apéndice\ ref {eqn:law_tot_prob}). Por lo tanto, las frecuencias de los tres genotipos posibles pueden escribirse como se da en la Tabla\ ref {tabla:generalizedHwe}, que proporciona una generalización de las proporciones Hardy-Weinberg.
La frecuencia del\(A_1\) alelo se encuentra\(p\) en un locus bialélico. Supongamos que nuestra población se aparea aleatoriamente y que las frecuencias de genotipos en la población siguen de HW. Seleccionamos dos individuos al azar para aparearse de esta población. Entonces apareamos a los niños de esta cruz. ¿Cuál es la probabilidad de que el niño de este apareamiento completo de hermanos sea homocigótico?
Múltiples bucles de endogamia en un pedigrí
Hasta este punto hemos asumido que hay a lo sumo un bucle endogamia en la historia familiar reciente de nuestros individuos, es decir, los padres de nuestro individuo endogámico tienen a lo sumo una conexión genealógica reciente. Sin embargo, un individuo que tiene múltiples bucles endogamia en su pedigrí puede ser homocigoto por descenso gracias a recibir alelos de EII a través de múltiples bucles diferentes. Para calcular la endogamia en pedigríes de complejidad arbitraria, podemos extender más allá de nuestros coeficientes de relación originales\(r_0\)\(r_1\), y\(r_2\) dar cuenta de la distribución de alelos de orden superior de EII entre familiares. Por ejemplo, podemos preguntarnos, ¿cuál es la probabilidad de que ambos alelos en el primer individuo sean compartidos EII con un alelo en el segundo individuo? Hay nueve posibles coeficientes de relación en total para describir completamente el parentesco entre dos individuos diploides, y no vamos a entrar a ellos aquí ya que es mucho de lo que hacer un seguimiento. Sin embargo, mostraremos cómo podemos calcular el coeficiente de endogamia de un individuo con múltiples bucles de endogamia más directamente.
Digamos que los padres de nuestro individuo endogámico (B y C) han\(K\) compartido antepasados, es decir, individuos que aparecen en los árboles genealógicos recientes de B y C. Denotamos estos antepasados compartidos por\(A_1, \dots,A_K\), y denotamos por\(n\) el número total de individuos en la cadena de B a C vía antepasado\(A_i\), incluyendo B, C, y\(A_i\). Por ejemplo, si B es la tía de C, entonces B y C comparten dos antepasados, que son los padres de B y, equivalentemente, los abuelos de C. En este caso, hay n=4 individuos de B a C a través de cada uno de estos dos ancestros compartidos. En el caso general, el coeficiente de parentesco de B y C, es decir, el coeficiente de endogamia de su hijo, es
\[F = \sum_{i=1}^K \frac{1}{2^{n_i}} \big( 1+ f_{A_i} \big) \label{eqn:inbreeding_over_ancs}\]
donde\(f_{A_i}\) está el coeficiente de endogamia del antepasado\(A_i\). Lo que sucede aquí es que sumamos todos los caminos mutuamente exclusivos en el pedigrí a través de los cuales B y C pueden compartir un alelo IBD. Con probabilidad\(\frac{1}{2^{n_i}}\), un par de alelos escogidos al azar de B y C desciende del mismo alelo ancestral en individuo\(A_i\), en cuyo caso los alelos son EII. Sin embargo, aunque B herede el alelo materno y C herede el alelo paterno de ancestro compartido\(A_i\), si ellos mismos\(A_i\) fueran endogámicos, con probabilidad\(f_{A_i}\) esos dos alelos sean ellos mismos EII. Así, un ancestro consanguíneo compartido aumenta aún más el parentesco de B y C.
Múltiples bucles de endogamia aumentan la probabilidad de que un niño sea homocigoto por descenso en un locus, lo que puede calcularse simplemente enchufando\(F\), el coeficiente de endogamia del niño, en nuestra ecuación de HW generalizada.
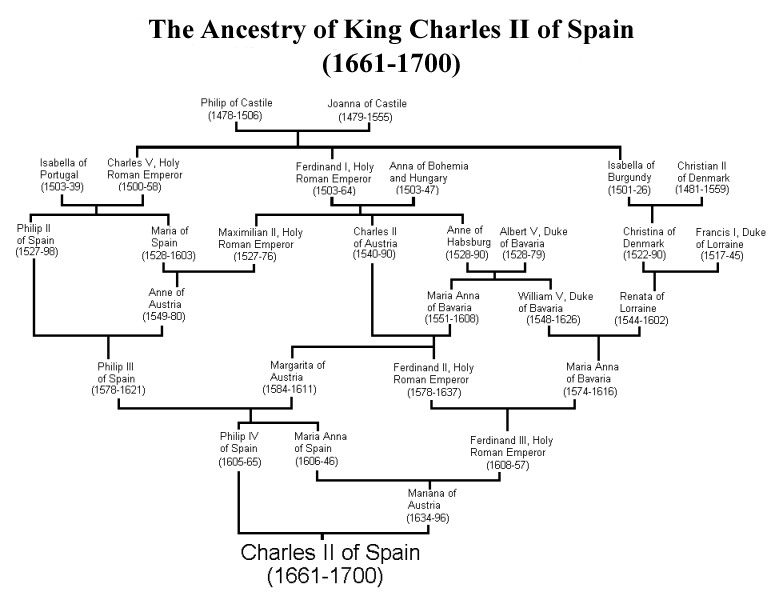
Como un ejemplo extremo del impacto de múltiples bucles de endogamia en el pedigrí de un individuo, consideremos al rey Carlos II de España, el último de los Habsburgo españoles. Carlos era hijo de Felipe IV de España y Mariana de Austria, que eran tío y sobrina. Si este fuera el único bucle de endogamia, entonces Charles habría tenido un coeficiente de endogamia de\(\frac{1}{8}\). Desafortunadamente para Carlos, los Habsburgo españoles habían mantenido durante mucho tiempo la riqueza y el poder dentro de su familia al concertar matrimonios entre parientes cercanos. El pedigrí de Carlos II se muestra en la Figura\ ref {fig:Carlos_second_pedigree}, y son aparentes múltiples bucles de endogamia. Por ejemplo, Felipe III, abuelo y bisabuelo de Carlos II, era él mismo hijo de un matrimonio tío-sobrina.
calculó que Carlos II tenía un coeficiente de endogamia de\(0.254\), equivalente a un apareamiento de sib completo, gracias a todos los bucles de endogamia en su pedigrí. Por lo tanto, se espera que haya sido homocigótico por descendencia durante una cuarta parte completa de su genoma. Como hablaremos más adelante en estas notas, esto significa que Charles pudo haber sido homocigótico para una serie de alelos de enfermedades recesivas, y de hecho era un hombre muy enfermizo que no dejó descendientes por su infertilidad. Así, plausiblemente, el fin de una de las grandes dinastías europeas se produjo a través de la endogamia.
Cálculo de coeficientes endogamia a partir de datos
Si la heterocigosidad observada en una población es\(H_O\), y asumimos que las proporciones generalizadas de Hardy-Weinberg se mantienen, podemos establecer\(H_O\) iguales a\(f_{12}\), y resolver la Ecuación\ ref {eq:HetgenHW}\(F\) para obtener una estimación de la coeficiente de endogamia como
\[\hat{F} = 1-\frac{f_{12}}{2pq} = \frac{2pq - f_{12}}{2pq}. \label{eqn:Fhat}\]
Como antes,\(p\) es la frecuencia del alelo\(A_{1}\) en la población. Esto puede ser reescrito en términos de la heterocigosidad observada (\(H_O\)) y la heterocigosidad esperada en ausencia de endogamia,\(H_E=2pq\), como
\[\hat{F} = \frac{H_E-H_O}{H_E} = 1 - \frac{H_O}{H_E}. \label{eqn:FhatHO}\]
De ahí\(\hat{F}\) que cuantifique la desviación por endogamia de la heterocigosidad observada de la esperada bajo apareamiento aleatorio, relativa a esta última.
Supongamos que se observaron las siguientes frecuencias de genotipo para un locus de esterasa en una población de Drosophila (A denota el alelo “rápido” y B denota el alelo “lento”):
| AA | AB | BB |
|---|---|---|
| 0.6 | 0.2 | 0.2 |
¿Cuál es la estimación del coeficiente de endogamia en el locus de esterasa?
Si tenemos múltiples loci, podemos reemplazar\(H_O\) y\(H_E\) por sus medios sobre loci,\(\bar{H}_O\) y\(\bar{H}_E\), respectivamente. Tenga en cuenta que, en principio, también podríamos calcular primero\(F\) para cada locus individual, y luego tomar el promedio a través de loci. Sin embargo, este procedimiento es más propenso a introducir un sesgo si los tamaños de las muestras varían según los loci, lo que no es poco probable cuando se trata de datos reales.
Los marcadores genéticos se utilizan comúnmente para estimar la endogamia para poblaciones silvestres y/o cautivas de interés para la conservación. Como ejemplo de ello, consideremos el caso del lobo mexicano (Canis lupus baileyi), una subespecie de lobo gris.

Fueron extirpados en estado silvestre a mediados del siglo XX debido a la caza, y los cinco lobos mexicanos restantes en la naturaleza fueron capturados para iniciar un programa de reproducción. Estimó que el día actual, la heterocigosidad promedio esperada era\(0.18\), con base en frecuencias alélicas en más de cuarenta mil SNP. Sin embargo, solo se observó que el individuo promedio de lobo mexicano era heterocigoto en\(12\%\) estos SNP. Por lo tanto, el coeficiente promedio de endogamia para el lobo mexicano es\(\hat{F} = 1 -\frac{0.12}{0.18}\), es decir\(\sim 33 \%\), del genoma de un lobo es homocigótico debido a la reciente endogamia en su pedigrí.
Bloques genómicos de homocigosidad por endogamia.
Como vimos anteriormente, se espera que familiares cercanos compartan alelos EII en grandes bloques genómicos. Así, cuando los individuos relacionados se aparean y transmiten alelos a una descendencia endogámica, transmiten estos alelos en grandes bloques a través de la meiosis. Como ejemplo, volvamos al caso de nuestros hipotéticos primos hermanos de la Figura\ ref {fig:IBD_Cousins_CHR_Cartoon}. Si este par de individuos tuvo un hijo, se muestra un posible patrón de transmisión genética en la Figura\ ref {fig:kid_first_cousins}. El niño ha heredado el tramo rojo del cromosoma a través de dos rutas diferentes a través de su predigrí de los abuelos. Este es un ejemplo de un segmento autocigótico, donde el niño es homocigótico por descenso en todos los loci de esta región roja.
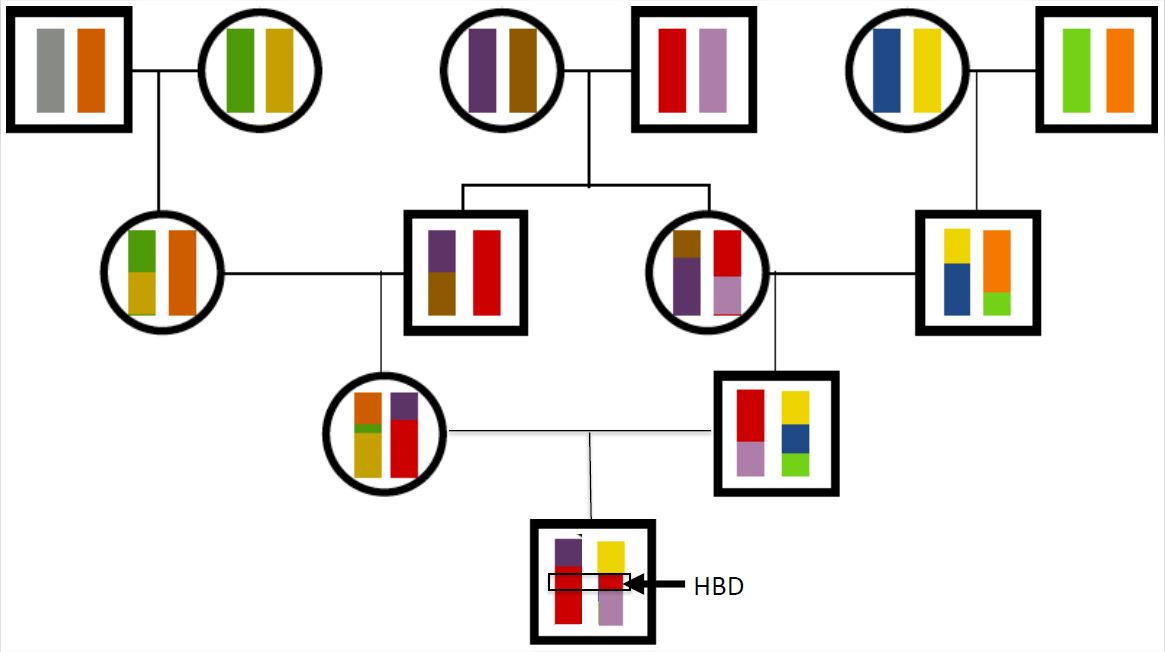
El coeficiente de endogamia del niño establece la proporción de su genoma que estará en estos segmentos autozigóticos. Por ejemplo, se espera que un hijo de primos hermanos completos tenga\(1/16\) de su genoma en estos segmentos. Cuanto más distante esté el bucle en el pedigrí, más meiosis por las que han pasado los cromosomas y más cortos serán los bloques individuales. Un hijo de primos hermanos tendrá bloques más largos que un hijo de primos segundos, por ejemplo.
Los individuos con múltiples bucles de endogamia en su árbol genealógico pueden tener un alto coeficiente de endogamia debido al efecto combinado de muchos pequeños bloques de autocigosidad. Por ejemplo, Carlos II tenía un coeficiente de endogamia que es equivalente al del hijo de hermanos completos, con una cuarta parte de su genoma esperado homocigoto por descendencia, pero esto estaría conformado por muchos bloques más cortos.
Podemos esperar detectar estos bloques buscando series genómicas inusualmente largas de sitios de homocigosidad (ROH) en el genoma de un individuo. Una manera de estimar el coeficiente de endogamia de un individuo es entonces totalizar la proporción del genoma de un individuo que cae en dichas regiones ROH. Esta estimación se llama\(F_{ROH}\).
Un ejemplo de uso\(F_{ROH}\) para estudiar la endogamia proviene del trabajo de, quien identificó corridas de homocigosidad en 2,500 perros, que van desde los 500kb hasta muchos megabases.
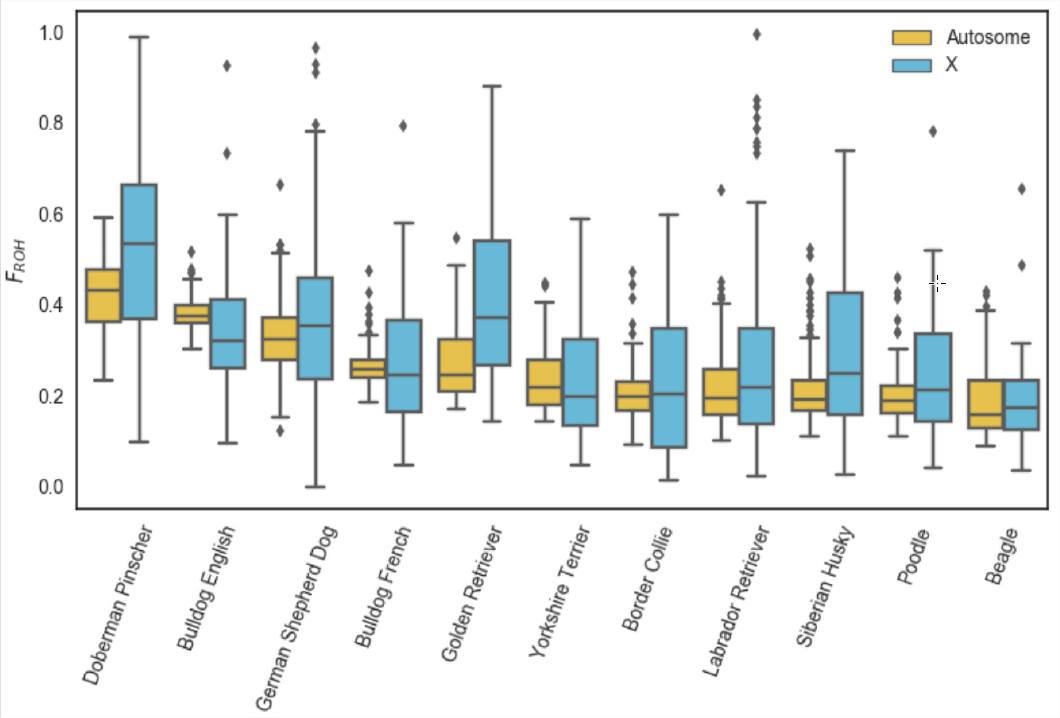
La Figura\ ref {fig:Dog_FOH} muestra la distribución\(F_{ROH}\) de los individuos en cada raza canina para la X y el autosoma. En la Figura\ ref {fig:DOG_FOH_DIST} esto se desglosa por la longitud de los segmentos ROH.
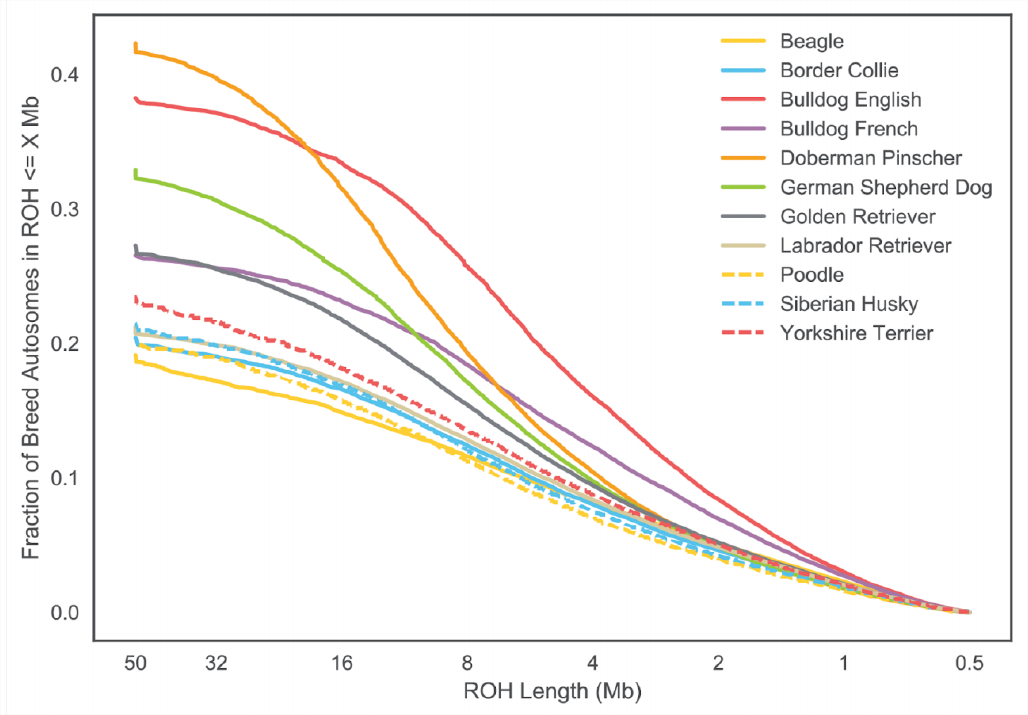
perros (\ PloSCBY). Tenga en cuenta que las longitudes más largas de ROH están a la izquierda de la parcela.
Las razas de perros han sido objeto de una reproducción intensa que ha dado como resultado altos niveles de endogamia. De las muestras poblacionales examinadas, los Doberman Pinschers tienen los niveles más altos de su genoma en series de homocigosidad (\(F_{ROH}\)), algo mayores que los bulldogs ingleses. En\ ref {fig:DOG_FOH_DIST} podemos ver que los bulldogs ingleses tienen más ROH cortos que Doberman Pinschers, pero que Doberman Pinschers tienen más de su genoma en ROH muy grande (\(>16 Mb\)). Esto sugiere que los bulldogs ingleses han tenido una larga historia de endogamia ya que tienen muchos bloques pequeños, pero que Doberman Pinschers tienen mucha endogamia reciente ya que su autocigosidad está contenida en bloques largos relativamente intactos por recombinación.
Resumen
- En este capítulo se desarrolló la relación entre las frecuencias alélicas y las frecuencias de genotipos dentro de una generación y entre parientes.
- Bajo apareamiento aleatorio, derivamos expectativas de las frecuencias de genotipo (Hardy-Weinberg), y podemos identificar desviaciones de estas expectativas.
- La identidad por ascendencia (EII) se refiere al intercambio de alelos debido a una reciente relación biológica compartida.
- Podemos predecir la probabilidad y el nivel esperado de compartir los alelos EII entre pares de parientes usando probabilidades de transmisión mendeliana (tal como están contenidas en los coeficientes\(r_0\)\(r_1\), y\(r_2\)). Un resumen útil de la relación para un par de individuos es el coeficiente de parentesco\(F_{i,j}\).
- También podemos aprender sobre las relaciones genéticas a partir del intercambio de segmentos genómicos entre familiares, con muchos segmentos compartidos largos revelando una relación más estrecha.
- Un individuo consanguíneo tiene padres que están más estrechamente relacionados que los sorteos aleatorios de alguna población de referencia.
- La endogamia da como resultado una disminución de la heterocigosidad y un aumento complementario de la homocigosidad. Podemos utilizar el coeficiente de parentesco de los padres para estimar la distorsión lejos de Hardy-Weinberg y el nivel esperado de heterocigosidad.
- Los coeficientes de endogamia se pueden calcular a partir de datos genéticos, ya sea para múltiples individuos en un solo locus o para múltiples loci para un solo individuo.
Calcular\(r_{0}\)\(r_{1}\),,\(r_{2}\) y el coeficiente de parentesco\(F\) entre:
- Un abuelo y su nieto
- Un bisabuelo y su bisnieto
- Hermanos completos
- Una tía abuela y su sobrino nieta (tu tía abuela = la tía de tus padres)
Estás estudiando un polimorfismo de color de flor codominante. Saltando por un prado de flores y compilar los siguientes datos:
| rojo | rosa | blanco |
| 200 | 100 | 200 |
- ¿Qué frecuencias esperarías en este locus bajo equilibrio Hardy-Weinberg?
- Calcular el coeficiente de endogamia en este locus.
- Nombra dos procesos distintos que puedan llevar a la desviación que ves, y describe cómo resultarían en un déficit de heterocigotos.
¿Cuáles son los coeficientes de relación del cromosoma X entre:
- ¿Dos hermanos varones completos?
- ¿Dos hermanos femeninos completos?
- ¿Cuál es la probabilidad de que una descendencia femenina de un apareamiento completo de sib sea homocigótica por descenso en un locus en su cromosoma X?
Estás estudiando el polimorfismo de la mancha alera en una especie de mariposa. A partir de cruces en el laboratorio se encuentra que la presencia de manchas alares está determinada por un alelo dominante.
Colectas 100 mariposas, 84 de ellas tienen las manchas de las alas. ¿Cuál es la frecuencia del alelo de punto de ala? ¿Qué suposición tuviste que hacer para llegar a tu respuesta?
Un alelo tiene frecuencia de\(0.001\) en la población. ¿Cuál es la probabilidad de que tanto tú como tu primo primero (completo) sean heterocigotos para el alelo?
El coeficiente de parentesco de los padres es el coeficiente de endogamia de la descendencia. Explicar, con referencia a la ponderación de los coeficientes de relación en el coeficiente de endogamia, por qué el coeficiente de endogamia es la probabilidad de que un locus sea homocigoto por descenso.
En términos de identidad por descendencia, explicar por qué múltiples bucles de endogamia en el pedigrí de un individuo conducen a niveles más altos de endogamia.


