4: Deriva Genética y Diversidad Neutra
- Page ID
- 58053
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La aleatoriedad es inherente a la evolución, desde las aves afortunadas que se desviaron de rumbo hasta colonizar alguna nueva isla oceánica, a la que surgen mutaciones primero en la cepa del VIH que infecta a un individuo que toma medicamentos antirretrovirales. Una fuente importante de estocástica en la biología evolutiva es la deriva genética. La deriva genética ocurre porque más o menos copias de un alelo por casualidad pueden transmitirse a la siguiente generación. Esto puede ocurrir porque, por casualidad, los individuos portadores de un alelo particular pueden dejar más o menos descendencia en la próxima generación. En una población sexual, la deriva genética también ocurre porque la transmisión mendeliana significa que solo uno de los dos alelos en un individuo, elegido al azar en un locus, se transmite a la descendencia.
La deriva genética puede jugar un papel en la dinámica de todos los alelos en todas las poblaciones, pero jugará el papel más importante para los alelos neutros. Un polimorfismo neutro ocurre cuando los alelos segregantes en un sitio polimórfico no tienen diferencias discernibles en su efecto sobre la aptitud. Dejaremos claro lo que queremos decir con “discernible” más adelante, pero por el momento pensaremos en esto como “ningún efecto” en el fitness.
La teoría neutra de la evolución molecular
El papel de la deriva genética en la evolución molecular se ha debatido acaloradamente desde los años 60 cuando se propuso la teoría neutra de la evolución molecular. La premisa central de la teoría neutra es que los patrones de polimorfismo molecular dentro de las especies y la sustitución entre especies se pueden entender bien suponiendo que la gran mayoría de estos polimorfismos moleculares y sustituciones fueron alelos neutros, cuya dinámica solo estuvo sujeta a los caprichos de deriva genética y mutación. Los primeros defensores de este punto de vista sugirieron que la gran mayoría de las nuevas mutaciones son neutras o altamente deletéreas (por ejemplo, mutaciones que interrumpen funciones importantes de las proteínas). Esta última clase de mutaciones son demasiado perjudiciales para contribuir mucho a polimorfismos comunes o sustituciones entre especies, ya que son rápidamente eliminadas de la población por selección.
La teoría neutra puede sonar extraña dado que gran parte del tiempo nuestro primer pincel con la evolución a menudo se centra en la adaptación y la evolución fenotípica. Sin embargo, los defensores de esta visión del mundo no negaron la existencia de mutaciones ventajosas, simplemente pensaron que las mutaciones beneficiosas son lo suficientemente raras como para que su contribución a la mayor parte del polimorfismo o divergencia pueda ser ignorada en gran medida. También a menudo pensaban que gran parte de la evolución fenotípica bien puede ser adaptativa, pero nuevamente los loci responsables de estos fenotipos son una pequeña fracción de todo el cambio molecular que se produce. La teoría neutra de la evolución molecular se propuso originalmente para explicar el polimorfismo proteico. Sin embargo, podemos aplicarlo de manera más amplia para pensar en la evolución neutra en todo el genoma. Con eso en mente, ¿qué tipos de cambios moleculares podrían ser neutros? Tal vez:
- Cambios en el ADN no codificante que no interrumpen las secuencias reguladoras. Por ejemplo, en el genoma humano solo alrededor del 2% del genoma codifica proteínas. El resto se compone mayoritariamente de elementos transponibles antiguos e inserciones de retrovirus, repeticiones, pseudo-genes y desorden genómico general. Las estimaciones actuales sugieren que, incluso contando regiones conservadas, funcionales y no codificantes, menos del 10% de nuestro genoma está sujeto a restricciones evolutivas.
- Cambios sinónimos en las regiones codificantes, es decir, aquellas que no cambian el amino ácido codificado por un codón.
- Cambios no sinónimos que no tienen un fuerte efecto sobre las propiedades funcionales del aminoácido codificado, por ejemplo, cambios que no cambian demasiado el tamaño, la carga o las propiedades hidrófobas del aminoácido.
- Un cambio de aminoácidos con consecuencias fenotípicas, pero poca relevancia para la aptitud física, por ejemplo, una mutación que hace que tus oídos tengan una forma ligeramente diferente, o que impida que un organismo viva más de 50 años en una especie donde la mayoría de los individuos se reproducen y mueran a los 20 años.
Hay ejemplos contrarios a todas estas ideas, por ejemplo, los cambios sinónimos pueden afectar la velocidad de traducción y la precisión de las proteínas y, por lo tanto, están sujetos a selección. Sin embargo, la lista anterior ojalá le convenza de que el pensamiento general de que alguna porción del cambio molecular puede no estar sujeta a selección no es tan tonta como pudo haber sonado inicialmente.
Diversas características del polimorfismo molecular y la divergencia se han visto como consistentes con la teoría neutra de la evolución molecular. En este capítulo nos centraremos en la predicción de un alto nivel de polimorfismo molecular en muchas especies (ver por ejemplo Figura\ ref {fig:Leffer}). En un capítulo posterior hablaremos sobre la predicción de un reloj molecular. Veremos que diversos aspectos de la teoría neutra original tienen mérito en describir algunas características y tipos de cambio molecular, pero también veremos que es demostrablemente erróneo en algunos casos. También veremos que la utilidad primaria de la teoría neutral no es si es correcta o incorrecta, sino que sirve como un simple modelo nulo que puede ser probado y en algunos casos rechazado, y posteriormente construido sobre él. El debate más amplio actualmente en el campo de la evolución molecular es el equilibrio de cambios neutros, adaptativos y nocivos que impulsan diferentes tipos de cambio evolutivo.
Pérdida de heterocigosidad por deriva
La deriva genética, en ausencia de nuevas mutaciones, purgará lentamente nuestra población de diversidad genética neutra, ya que los alelos se desplazan lentamente a frecuencias altas o bajas y se pierden o se fijan con el tiempo.
Imagínese una población de apareamiento aleatorio de individuos\(N\) diploides de tamaño constante, y que estamos examinando un locus que segrega para dos alelos que son neutros entre sí. Esta población se aparea aleatoriamente con respecto a los alelos en este locus. Ver Figuras Figura\(\PageIndex{1}\) y Figura\(\PageIndex{2}\) para ver cómo procede la deriva genética, mediante el seguimiento de alelos dentro de una pequeña población.
En generación\(t\) nuestro nivel actual de heterocigosidad es\(H_t\), es decir, la probabilidad de que dos alelos muestreados aleatoriamente en generación no\(t\) sean idénticos es\(H_t\). Suponiendo que la tasa de mutación es cero (o desaparecidamente pequeña), ¿cuál es nuestro nivel de heterocigosidad en la generación\(t+1\)?
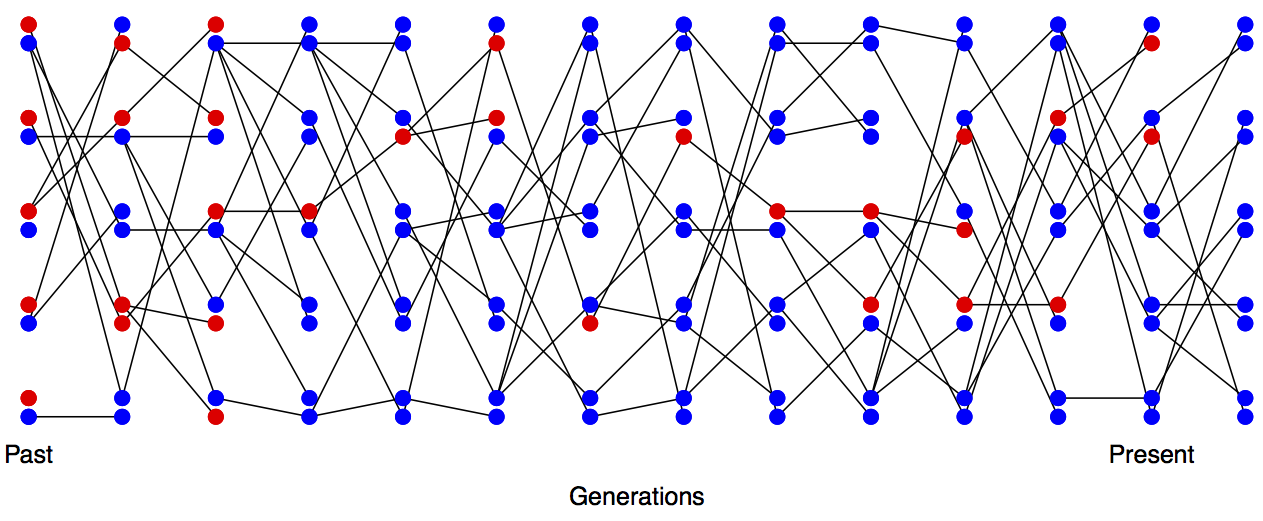
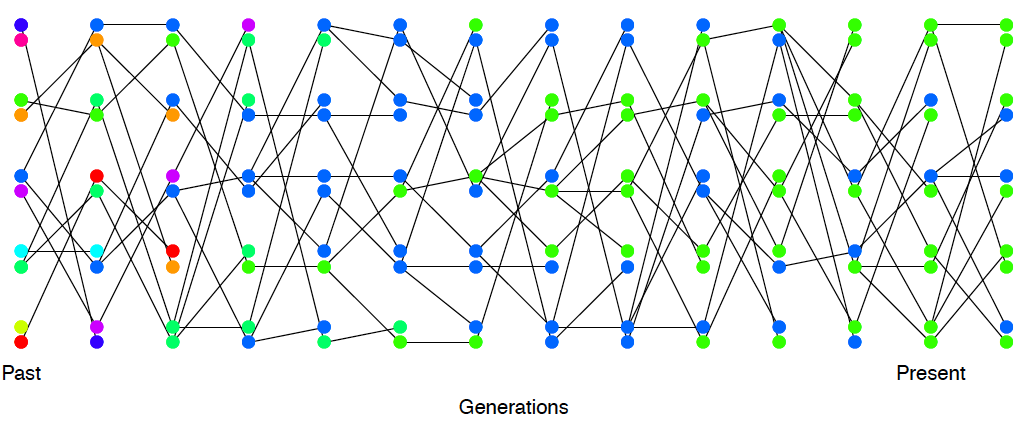
En la siguiente generación (\(t+1\)) estamos viendo los alelos en la descendencia de generación\(t\). Si muestreamos aleatoriamente dos alelos en generación\(t+1\) que tenían diferentes alelos parentales en generación\(t\), eso es como dibujar dos alelos aleatorios de generación\(t\). Entonces la probabilidad de que estos dos alelos en generación\(t+1\), que tienen diferentes alelos parentales en generación\(t\), no sean idénticos es\(H_t\).
Por el contrario, si los dos alelos de nuestro par tenían el mismo alelo parental en la generación siguiente (es decir, los alelos son idénticos por descendencia una generación atrás) entonces estos dos alelos deben ser idénticos (ya que no estamos permitiendo ninguna mutación).
En una población diploide de\(N\) individuos de tamaño hay\(2N\) alelos. La probabilidad de que nuestros dos alelos tengan el mismo alelo parental en la generación siguiente es\(\frac{1}{(2N)}\) y la probabilidad de que tengan diferentes alelos parentales es es\(1-\frac{1}{(2N)}\). Entonces, por el argumento anterior, la heterocigosidad esperada en la generación\(t+1\) es
\[H_{t+1} = \frac{1}{2N} \times 0 + \left(1-\frac{1}{2N} \right)H_t\]
Así, si la heterocigosidad en la generación\(0\) es\(H_0\), nuestra heterocigosidad esperada en la generación\(t\) es
\[H_t = \left(1-\frac{1}{2N} \right)^tH_0 \label{eqn:loss_het_discrete}\]
es decir, la heterocigosidad esperada dentro de nuestra población está decayendo geométricamente con cada generación que pasa. Si asumimos que\(\frac{1}{(2N)} \ll 1\) entonces podemos aproximar esta decadencia geométrica por una decaimiento exponencial (ver Pregunta\ ref {geoquestion} abajo), tal que
\[H_t =H_{0} e^{ - \frac{t}{(2N)} }\]
es decir, la heterocigosidad decae exponencialmente a una velocidad\(\frac{1}{(2N)}\).
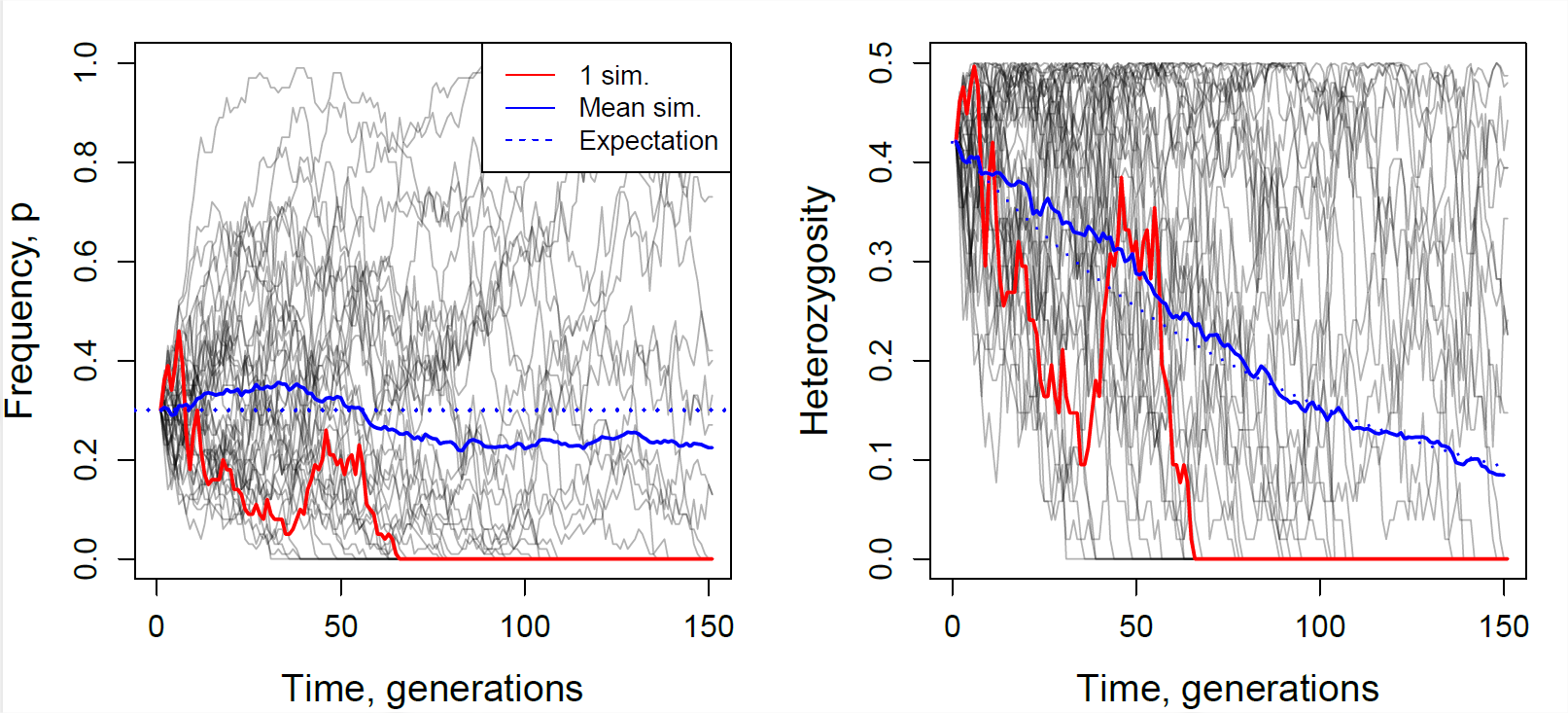
En la Figura\ ref {fig:Losshet_WF_N50} mostramos trayectorias a través del tiempo para 40 loci simulados independientemente a la deriva en una población de 50 individuos. Cada población se inició a partir de una frecuencia de\(30\%\). Algunos van hacia arriba y otros bajan, eventualmente se pierden o se fijan de la población, pero, en promedio a través de simulaciones, la frecuencia alélica no cambia. También rastreamos la heterocigosidad, se puede ver que la heterocigosidad a veces sube, y a veces baja, pero en promedio estamos perdiendo heterocigosidad, y esta tasa de pérdida está bien predicha por la Ecuación\ ref {eqn:loss_het_discrete}.
Usted es el encargado de mantener una población de olía delta en el delta del río Sacramento. Usando un gran conjunto de microsatélites se estima que el nivel medio de heterocigosidad en esta población es 0.005. Te pones el objetivo de mantener un nivel de heterocigosidad de al menos 0.0049 durante los próximos doscientos años. Suponiendo que el olfato tenga un tiempo de generación de 3 años, y que solo la deriva genética afecte a estos loci, ¿cuál es la población totalmente exogamia más pequeña que necesitarías mantener para cumplir con este objetivo?
Observe cómo esta imagen de heterocigosidad decreciente se encuentra en contraste con la consistencia del equilibrio de Hardy-Weinberg del capítulo anterior. Sin embargo, nuestras proporciones de Hardy-Weinberg aún se mantienen en la formación de cada nueva generación. Como los genotipos de descendencia en la siguiente generación (\(t+1\)) representan un sorteo aleatorio de la generación anterior (\(t\)), si la frecuencia parental es\(p_t\), esperamos que una proporción\(2p_t(1-p_t)\) de nuestra descendencia sea heterocigotos (y Proporciones HW para nuestros homocigotos). Sin embargo, debido a que el tamaño de la población es finito, las frecuencias de genotipos observadas en la descendencia (probablemente) no coincidirán exactamente con nuestras expectativas. Como es probable que las frecuencias de nuestros genotipos cambien ligeramente debido al muestreo, esto refleja biológicamente la variación aleatoria en el tamaño de la familia y la segregación mendeliana, la frecuencia del alelo cambiará. Por lo tanto, mientras que cada generación representa una muestra de proporciones de Hardy-Weinberg basadas en la generación anterior, nuestras proporciones de genotipos no están en equilibrio (un estado inmutable) ya que la frecuencia alélica subyacente cambia a lo largo de las generaciones. Desarrollaremos algunos modelos matemáticos para estos cambios de frecuencia alélica más adelante. Por ahora, simplemente notaremos que bajo nuestro modelo simple de deriva (formalmente el modelo Wright-Fisher), nuestro recuento de alelos en la\(t+1^{th}\) generación representa una muestra binomial (de tamaño\(2N\)) de la frecuencia poblacional\(p_t\) en la generación anterior. Si has leído hasta aquí, por favor envía un correo electrónico al Prof Coop una foto de JBS Haldane en traje a rayas con el título “Estoy leyendo las notas del capítulo 3". (Vale la pena buscar en Google a JBS Haldane y leer más sobre su vida; es un verdadero personaje y uno de los últimos grandes polímatos).
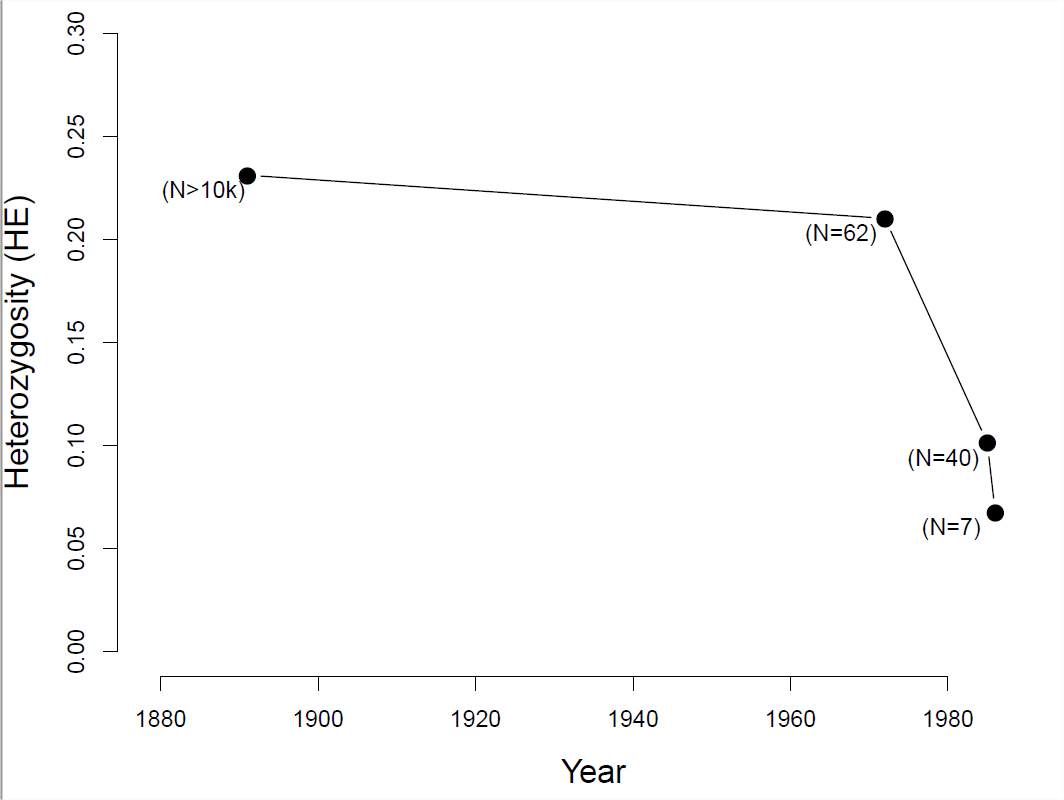
Para ver cómo una disminución en el tamaño de la población puede afectar los niveles de heterocigosidad, consideremos el caso de los hurones de patas negras (Mustela nigripes). La población de hurones de patas negras ha disminuido drásticamente a lo largo del siglo XX debido a la destrucción de su hábitat y a la peste silvestre. En 1979, cuando el último hurón de patas negras conocido murió en cautiverio, se pensó que estaban extintos. En 1981, se redescubrió una población silvestre muy pequeña (\(40\)individuos), pero en 1985 esta población sufrió una serie de brotes de enfermedades.
En ese punto de los\(18\) restantes individuos silvestres fueron llevados en cautiverio, de los cuales 7 reproducidos. Gracias a los intensos esfuerzos de cría en cautividad y al trabajo de conservación, desde entonces se ha establecido una población silvestre de más de 300 individuos. Sin embargo, debido a que todos estos individuos descienden de esos 7 individuos que sobrevivieron al cuello de botella, los niveles de diversidad siguen siendo bajos. Mide heterocigosidad en varios microsatélites en individuos de colecciones de museos, mostrando la fuerte caída de la diversidad a medida que el tamaño de la población se estrelló (ver Figura\ ref {fig:Losshet_hurones}).
En genética matemática de poblaciones, una aproximación comúnmente utilizada es\((1-x) \approx e^{-x}\) para\(x << 1\) (formalmente, esto se desprende de la expansión de la serie Taylor de\(\exp(-x)\), ignorando términos de segundo orden y superiores de\(x\), ver Apéndice\ ref {EQN:Taylor_geo}). Esta aproximación es especialmente útil para aproximar un proceso de decaimiento geométrico mediante un proceso de decaimiento exponencial,\((1 - x)^t \approx e^{-xt}\) p. Usando su calculadora, o R, verifique qué tan bien esta expresión se aproxima a la expresión exacta para dos valores de\(x\),\(x = 0.1\), y\(0.01\), a través de dos valores diferentes de t,\(t=5\) y\(t=50\). Comenta brevemente tus resultados.
Niveles de diversidad mantenidos por un equilibrio entre mutación y deriva
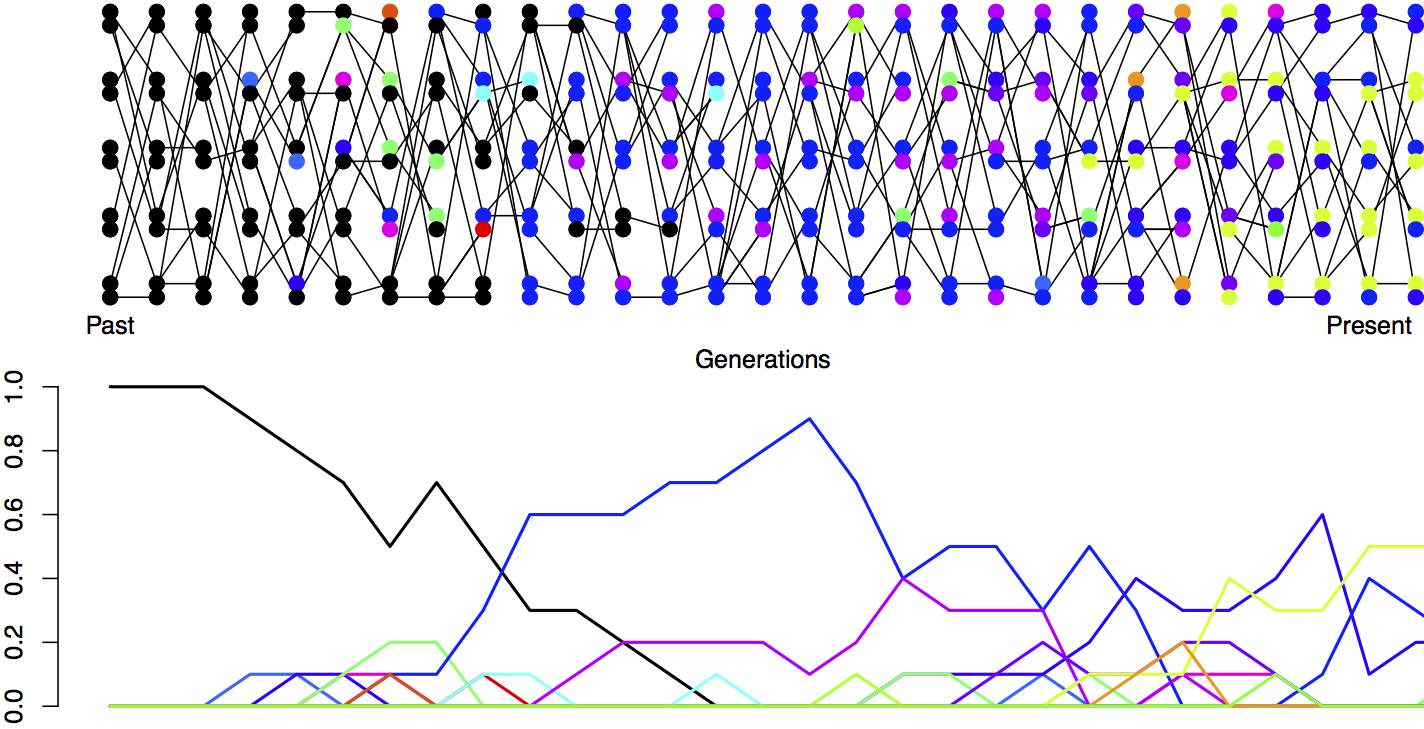
A continuación vamos a considerar la cantidad de polimorfismo neutro que se puede mantener en una población como un equilibrio entre variación de eliminación de deriva genética y mutación introduciendo nueva variación neutra, ver Figura\ ref {fig:mut_sel_balance} para un ejemplo. Nótese en nuestro ejemplo, cómo ningún alelo individual se mantiene en un equilibrio estable, sino que un nivel de equilibrio de polimorfismo se mantiene mediante un conjunto de alelos en constante cambio.
La tasa de mutación neutra
Primero vamos a querer considerar la velocidad a la que surgen las mutaciones neutras en la población.Pensando en nuestra discusión sobre la teoría neutra de la evolución molecular, supongamos que solo hay dos clases de mutación que pueden surgir en nuestra región genómica de interés: mutaciones neutras y altamente mutaciones deletéreas. La tasa de mutación total en nuestro locus es\(\mu\) por generación, es decir, por transmisión de padres a hijos. Una fracción\(C\) de nuestras mutaciones son alelos nuevos que son altamente deletéreos y que tan rápidamente se eliminan de la población. Llamaremos a este\(C\) parámetro la restricción, y diferirá según la región genómica que consideremos. La fracción restante\((1-C)\) son nuestras mutaciones neutras, tal que nuestra tasa de mutación neutra es\((1-C)\mu\). Esta es la tasa por generación. En el resto del capítulo por simplicidad asumiremos eso\(C=0\) y usaremos una tasa de mutación neutra de\(\mu\). Sin embargo, volveremos a esta discusión de restricción cuando discutamos la divergencia molecular en un capítulo posterior.
Vale la pena tomarse un minuto para familiarizarse tanto con lo rara como con lo común que es la mutación. La tasa de mutación por par base en humanos es de alrededor\(1.5\)\(\times\)\(10^{-8}\) por generación. Eso significa que, en promedio, tenemos que monitorear un sitio por\(\sim 66.6\) millones de transmisiones de padres a hijos para ver una mutación. Sin embargo, las poblaciones y los genomas son lugares grandes, por lo que las mutaciones son comunes en estos niveles.
- Tu genoma autosómico tiene\(\sim\) 3 mil millones de pares de bases de largo (\(3\)\(\times\)\(10^9\)). Tienes dos copias, la que recibiste de tu mamá y otra de tu papá. ¿Cuál es el promedio (es decir, el esperado) número de mutaciones que ocurrieron en la transmisión de tu mamá y tu papá a ti?
- El tamaño actual de la población humana es de\(\sim\) 7 mil millones de individuos. ¿Cuántas veces, a nivel de toda la población humana, un solo par de bases está mutado en la transmisión de una generación a la siguiente?
Niveles de heterocigosidad mantenidos como equilibrio entre mutación y deriva
Mirando hacia atrás en el tiempo de una generación a la generación anterior, vamos a decir que dos alelos que tienen el mismo alelo parental (es decir, encuentran a su ancestro común) en la generación anterior se han unido, y se refieren a este evento como un evento coalescente. Si nuestros pares de alelos van a ser diferentes entre sí en la actualidad, debe haber ocurrido una mutación más recientemente en uno u otro linaje antes de encontrar un ancestro común.
La probabilidad de que nuestro par de alelos muestreados aleatoriamente se hayan fusionado en la generación anterior es\(\frac{1}{(2N)}\), y la probabilidad de que nuestro par de alelos no se fusionen es\(1-\frac{1}{(2N)}\).
La probabilidad de que una mutación cambie la identidad del alelo transmitido es\(\mu\) por generación. Entonces la probabilidad de que no ocurra ninguna mutación es\((1-\mu)\). Supondremos que cuando ocurre una mutación crea algún nuevo tipo alélico que no está presente en la población. Esta suposición (comúnmente llamada el modelo infinitamente de muchos alelos) hace que las matemáticas sean un poco más limpias, y tampoco es una suposición demasiado mala biológicamente. Ver Figura\ ref {fig:mut_sel_balance} para una representación del equilibrio mutación-deriva en este modelo a lo largo de las generaciones.
Este modelo nos permite calcular cuándo nuestros dos alelos compartieron por última vez un ancestro común y si estos alelos son idénticos a consecuencia de no poder mutar desde este ancestro compartido. Por ejemplo, podemos calcular la probabilidad de que nuestros dos alelos muestreados aleatoriamente se unan\(2\) generaciones en el pasado (es decir, no logran fusionarse en generación\(1\) y luego fusionarse en generación\(2\)), y que sean idénticos a
\[\left(1- \frac{1}{2N} \right) \frac{1}{2N} (1-\mu)^4\]
Tenga en cuenta que el poder de\(4\) es porque nuestros dos alelos tienen que haber fallado en mutar a través de\(2\) meiosis cada uno.
Más generalmente, la probabilidad de que nuestros alelos se fusionen en generación\(t+1\) (contando hacia atrás en el tiempo) y sean idénticos debido a que no hay mutación en ninguno de los alelos en las generaciones posteriores es
\[\mathbb{P}(\textrm{coal. in t+1 \& no mutations}) = \frac{1}{2N} \left(1- \frac{1}{2N} \right)^t \left(1-\mu \right)^{2(t+1)}\]
Para que esto sea un poco más fácil para nosotros mismos, asumamos eso\(t \approx t+1\) y así reescribamos esto como:
\[\mathbb{P}(\textrm{coal. in t+1 \& no mutations}) \approx \frac{1}{2N} \left(1- \frac{1}{2N} \right)^t \left(1-\mu \right)^{2t}\]
Esto nos da la probabilidad aproximada de que dos alelos se fusionen en la\((t+1)^\text{th}\) generación. En general, puede que no sepamos cuándo pueden fusionarse dos alelos: podrían fusionarse en generación\(t=1, t=2, \ldots\), y así sucesivamente. Así, para calcular la probabilidad de que dos alelos se fusionen en cualquier generación antes de mutar, podemos escribir:
\[\begin{aligned} \mathbb{P}(\textrm{coal. in any generation \& no mutations}) \approx & \mathbb{P}(\textrm{coal. in} \; t=1 \; \textrm{\& no mutations}) \; + \nonumber\\ & \mathbb{P}(\textrm{coal. in} \; t=2 \; \textrm{\& no mutations}) + \ldots \nonumber\\ %P(\textrm{coal. in} \; t=3 \; \textrm{\& no mutations}) +\ldots \nonumber\\ = & \sum_{t=1}^\infty \mathbb{P}(\textrm{coal. in } \; t \; \textrm{generations \& no mutation})\end{aligned}\]
un ejemplo de uso de la Ley de Probabilidad Total, véase la Ecuación Apéndice\ ref {eqn:law_tot_prob}, combinada con el hecho de que la coalescencia en una generación en particular es mutuamente excluyente con la coalescencia en una generación diferente.
Si bien podríamos calcular un valor para esta suma dada\(N\) y\(\mu\), es difícil tener una idea de lo que está pasando con una expresión tan complicada. Aquí, pasamos a una aproximación común en genética de poblaciones (y todas las matemáticas aplicadas), donde asumimos que\(\frac{1}{(2N)} \ll 1\) y\(\mu \ll 1\). Esto nos permite aproximar la decadencia geométrica como una decaimiento exponencial (ver Apéndice Ecuación\ ref {EQN:Taylor_exp}). Entonces, la probabilidad de que dos alelos se fusionen en generación\(t+1\) y no muten se puede escribir como:
\[\begin{aligned} \mathbb{P}(\textrm{coal. in t+1 \& no mutations}) &\approx \frac{1}{2N} \left(1- \frac{1}{2N} \right)^t \left(1-\mu \right)^{2t} \\ & \approx \frac{1}{2N} e^{-t/(2N)} e^{-2\mu t } \\ &=\frac{1}{2N} e^{-t(2\mu+1/(2N))} \end{aligned}\]
Entonces podemos aproximar la suma por una integral, dándonos:
\[\frac{1}{2N} \int_0^{\infty} e^{-t(2\mu+1/(2N))} dt = \frac{1/(2N)}{1/(2N)+2\mu} \label{eqn:coal_no_mut}\]
La ecuación anterior nos da la probabilidad de que nuestros dos alelos se fusionen en algún momento, y no muten antes de llegar a su ancestro común. Equivalentemente, esto puede pensarse como la probabilidad de que nuestros dos alelos se fusionen antes de mutar, es decir, que sean homocigotos.
Entonces, la probabilidad complementaria de que nuestro par de alelos no sean idénticos (o heterocigotos) es simplemente uno menos esto. La siguiente ecuación da la heterocigosidad de equilibrio en una población en equilibrio entre mutación y deriva:
\[H = \frac{2\mu}{1/(2N)+2\mu} = \frac{4N\mu}{1+4N\mu} \label{eqn:hetero}\]
El parámetro compuesto\(4N\mu\), la tasa de mutación a escala poblacional, surgirá varias veces así que le daremos su propio nombre:
\[\theta = 4N\mu\]
Cuál es la intuición de nuestro\ ref {eqn:hetero}, bueno la probabilidad de que algún evento ocurra en una generación en particular es\(\mathbb{P}(\textrm{mutation or coalescence}) \approx \frac{1}{(2N)}+2\mu\), por lo que condicionada a que ocurra un evento la probabilidad de que sea una mutación es\(\mathbb{P}(\textrm{mutation} \mid \textrm{mutation or coalescence}) = \frac{2\mu}{\left(\frac{1}{(2N)}+2\mu \right)}\).
Entonces, siendo iguales, las especies con mayores tamaños de población deberían tener niveles proporcionalmente más altos de polimorfismo neutro. De hecho, las poblaciones de animales, por ejemplo aves, en islas pequeñas tienen menores niveles de diversidad que las especies estrechamente relacionadas en el continente con rangos más grandes. De manera más general, sí vemos mayores niveles de heterocigosidad en tamaños de población censales más grandes entre animales Figura\ ref {fig:alozyme_n}. Sin embargo, si bien el tamaño de la población censal varía en muchos órdenes de magnitud, los niveles de diversidad varían mucho menos que eso. Entonces, si los niveles de diversidad en poblaciones naturales representan un equilibrio entre deriva genética y mutación, los niveles de deriva genética en poblaciones grandes deben ser mucho más rápidos de lo que sugiere su tamaño poblacional censal. En la siguiente sección hablaremos de algunas posibles razones por las que.

El tamaño efectivo de la población
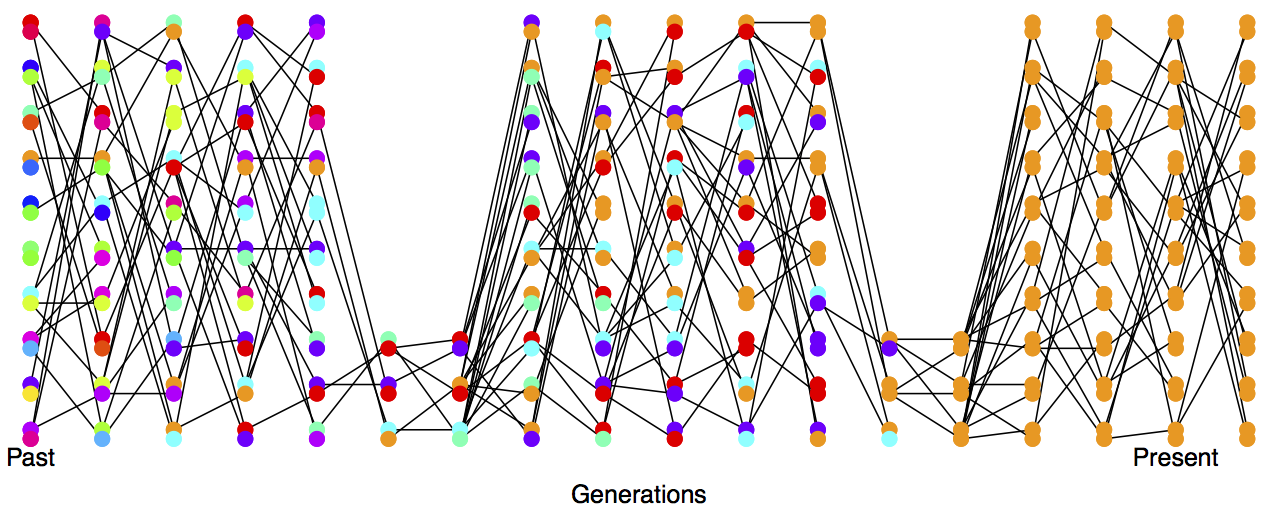
En la práctica, las poblaciones raramente se ajustan a nuestros supuestos de ser constantes en tamaño con baja varianza en el éxito reproductivo. Las poblaciones reales experimentan fluctuaciones dramáticas en el tamaño, y a menudo hay una alta varianza en el éxito reproductivo. Así, las tasas de deriva en las poblaciones naturales suelen ser mucho más altas de lo que implicaría el tamaño de la población censal. Ver Figura\ ref {fig:Losshet_varying_pop} para una representación de una población repetidamente cuellos de botella perdiendo diversidad a un ritmo rápido.
Para hacer frente a esta discrepancia, los genetistas poblacionales suelen invocar el concepto de un tamaño poblacional efectivo (\(N_e\)). En muchas situaciones (pero no en todas), las salidas de los supuestos del modelo pueden capturarse sustituyendo\(N_e\) por\(N\).
Si el tamaño de la población varía rápidamente en tamaño, podemos (si se cumplen ciertas condiciones) reemplazar el tamaño de nuestra población por el tamaño medio armónico de la población. Considerar una población diploide de tamaño variable, cuyo tamaño es de\(N_t\)\(t\) generaciones en el pasado. La probabilidad de que nuestros pares de alelos no se hayan fusionado por generación\(t\) viene dada por
\[\prod_{i=1}^{t} \left(1-\frac{1}{2N_i} \right) \label{eqn:var_pop_coal}\]
Tenga en cuenta que esto simplemente colapsa a nuestra expresión original\(\left(1-\frac{1}{2N } \right)^t\) si\(N_i\) es constante. Bajo este modelo, la tasa de pérdida de heterocigosidad en esta población es equivalente a una población de tamaño efectivo
\[N_e =\frac{1}{\frac{1}{t} \sum_{i=1}^{t} \frac{1}{N_i} }. \label{eq:Ne_harmonic}\]
Esta es la media armónica del tamaño variable de la población.
Así, el tamaño efectivo de nuestra población, el tamaño de una población constante idealizada que coincide con la tasa de deriva genética, es el tamaño promedio armónico de la población real a lo largo del tiempo. La media armónica se ve muy fuertemente afectada por valores pequeños, de tal manera que si el tamaño de nuestra población es\(99\%\) de un millón de veces pero desciende a\(1000\) cada cien o así generaciones,\(N_e\) estará mucho más cerca de un millón.\(1000\)
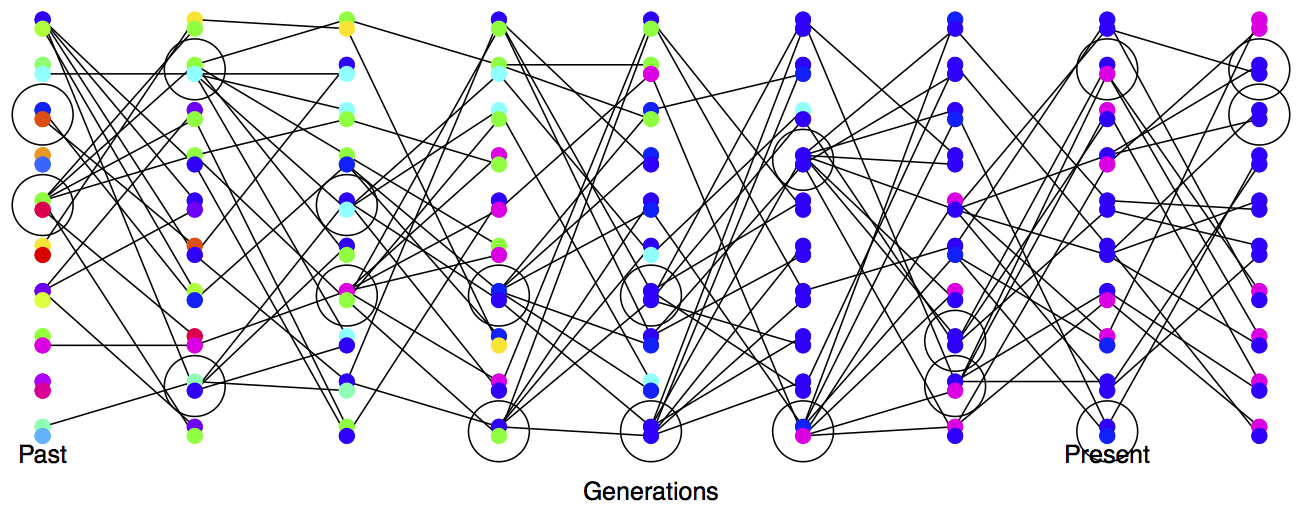
La varianza en el éxito reproductivo también afectará el tamaño efectivo de nuestra población. Incluso si nuestra población tiene\(N\) individuos de gran tamaño constante, si solo una pequeña proporción de ellos llega a reproducirse, entonces la tasa de deriva reflejará este número mucho menor de individuos reproductivos. Ver Figura\ ref {fig:Losshet_varying_RS} para una representación de la mayor tasa de deriva en una población donde hay alta varianza en el éxito reproductivo.
Para ver un ejemplo de esto, considere el caso donde\(N_F\) de las hembras llegan a reproducirse y\(N_M\) los machos se reproducen. Si bien cada individuo tiene una madre y un padre biológicos, no todos los individuos llegan a ser padres. En la práctica, en muchas especies animales se reproducen muchas más hembras que los machos, es decir\(N_M <N_F\), ya que algunos machos obtienen muchas oportunidades de apareamiento y muchos machos obtienen no/pocas oportunidades de apareamiento. Cuando nuestros dos alelos escogen a un antepasado,\(25\%\) de la época nuestros alelos estaban ambos en un antepasado femenino, en cuyo caso son IBD con probabilidad\(1/(2N_F)\), y\(25\%\) del tiempo ambos están en un ancestro masculino, en cuyo caso se fusionan con la probabilidad \(1/(2N_M)\). El resto\(50\%\) del tiempo, nuestros alelos se remontan a dos individuos de diferentes sexos en la generación anterior y así no pueden fusionarse. Por lo tanto, nuestra probabilidad de coalescencia en la generación anterior es
\[\frac{1}{4}\left(\frac{1}{2N_M} \right)+\frac{1}{4}\left(\frac{1}{2N_F} \right) %= %\frac{1}{8}\frac{N_F+N_M}{N_FN_M}\]
es decir, la tasa de coalescencia es la media armónica de los tamaños de población de los dos sexos, equiparándolo a\(\frac{1}{2N_e}\) lo que encontramos
[Fig:Hamadryas_babuino]
\[N_e = \frac{4N_FN_M}{N_F+N_M}\]
Por lo tanto, si el éxito reproductivo es muy sesgado en un solo sexo (e.g.\(N_M \ll N/2\)), nuestro tamaño de población autosómico efectivo se reducirá mucho como resultado. Para más información sobre cómo las diferentes fuerzas evolutivas afectan la tasa de deriva genética, y su impacto en el tamaño efectivo de la población, ver.
Estás estudiando una población de 500 babuinos Hamadryas machos y 500 hembras. Supongamos que todas las hembras pero sólo 1/10 de los machos llegan a aparearse. ¿Cuál es el tamaño efectivo de la población para el autosoma?
La varianza en el éxito reproductivo masculino y femenino puede tener efectos muy diferentes en los cromosomas con diferentes modos de herencia como el cromosoma X, las mitocondrias y el cromosoma Y. Las mitocondrias (ADNmt) y el cromosoma Y son haploides y solo se heredan a través de las hembras y los machos respectivamente, por lo que tienen una población haploide efectiva con tamaños de\(N_M\) y\(N_F\).

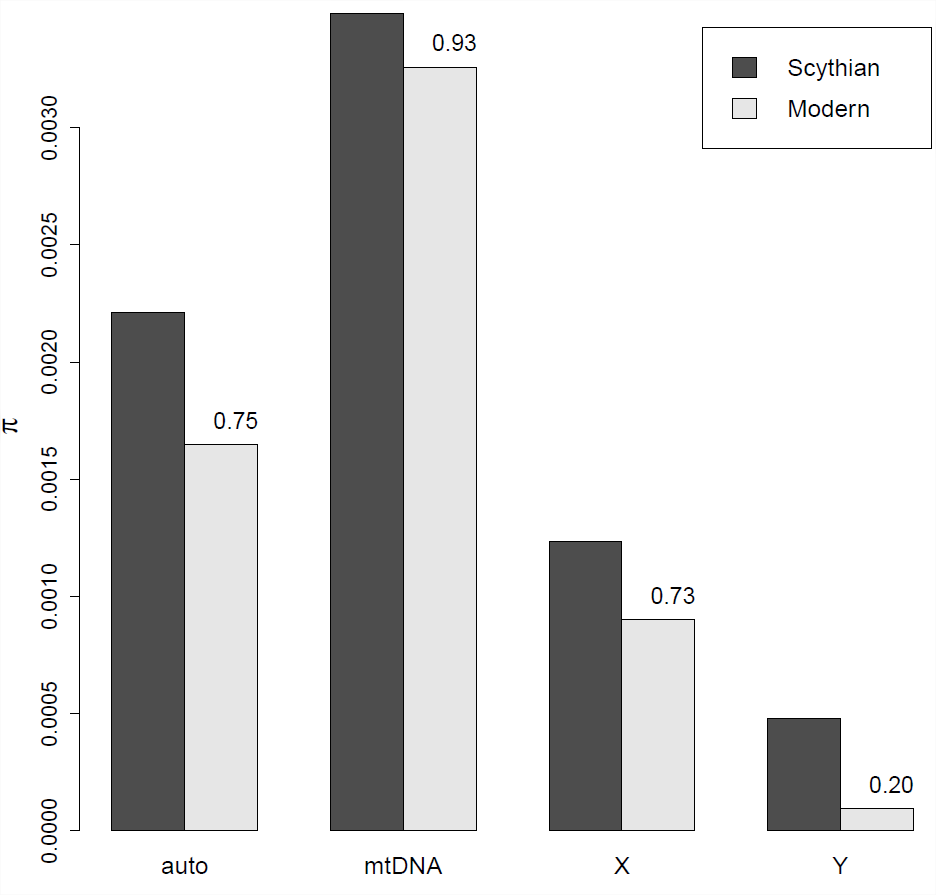 Niveles de diversidad genómica en caballos escitas de caballos escitas de caballos escitas de un\(2300\) año y caballos modernos (nórdicos). Los números al lado de cada columna dada la fracción de diversidad restante en la actualidad, Datos de.
Niveles de diversidad genómica en caballos escitas de caballos escitas de caballos escitas de un\(2300\) año y caballos modernos (nórdicos). Los números al lado de cada columna dada la fracción de diversidad restante en la actualidad, Datos de.Para ver el impacto de la varianza diferencial en el éxito reproductivo masculino y femenino, veamos cómo los niveles de diversidad genética a lo largo de miles de años en caballos domésticos.

secuenció ADN antiguo de 13 sementales sacrificados de un montículo funerario escita de un\(2300\) año de antigüedad en Kazajstán. Los escitas eran un pueblo nómada cuyo imperio estepario ruso se extendía desde el Mar Negro hasta las fronteras de China. Fueron de las primeras personas en dominar la guerra a caballo con hombres y mujeres montando armados con arcos cortos.
Al comparar estos datos con los caballos modernos, se encontró que los niveles de diversidad se habían reducido sustancialmente en los autosomas y muy reducidos en el cromosoma Y. Esto contrasta con el ADNmt donde los niveles de diversidad han disminuido solo ligeramente. Este patrón probablemente refleja el hecho de que gran parte de la cría moderna de caballos se basa en una cría de un pequeño número de sementales a un gran número de yeguas, y así el tamaño efectivo de la población del cromosoma Y ha sido mucho más pequeño que el ADNmt, lo que lleva a una tasa mucho mayor de pérdida de diversidad en el Y que en otros cromosomas.
Usando los datos sobre la reducción de la diversidad genética del caballo en la Figura\ ref {fig:Scythian_Horses_PI}:
- Estimar el número efectivo de sementales y yeguas que contribuyen a la población equina utilizando los datos del ADNmt y del cromosoma Y
- ¿Predecir cuál debería ser la reducción de la diversidad a lo largo de los\(2300\) años en los autosomas usando estos números?
Asumir un tiempo de generación de caballos de\(8\) años. Supongamos que no hay nuevas mutaciones durante este intervalo de tiempo.
Uno de los niveles más altos de diversidad genética se observa en el hongo diploide branquial dividido, Schizophyllum commune. Las poblaciones en Estados Unidos tienen una heterocigosidad a nivel de secuencia de\(0.13\) por base sinónima. padres secuenciados y múltiples crías para estimar eso\(\mu= 2 \times 10^{-8} bp^{-1}\) por generación. ¿Cuál es su estimación del tamaño efectivo de la población de S. commune?
_(33389628036).jpg)
Los coalescentes y patrones de diversidad neutra
“La vida solo se puede entender al revés; pero hay que vivirla hacia adelante” — Kierkegaard
Distribución del tiempo de coalescencia por pares y el número de diferencias por pares.
Pensando en nuestros cálculos que hicimos sobre la pérdida de heterocigosidad neutra y los niveles de equilibrio de diversidad (en las Secciones 1.1 y 1.1.1), notará que primero podríamos especificar en qué generación se fusionan un par de secuencias, y luego calcular algunas propiedades de heterocigosidad basada en eso. Eso es porque las mutaciones neutras no afectan la probabilidad de que un individuo transmita un alelo, y así no afectan la forma en que podemos rastrear linajes ancestrales a través de las generaciones.
Como tal, a menudo será útil considerar el tiempo al ancestro común de un par de secuencias (\(T_2\)), y luego pensar en el impacto de ese tiempo a la coalescencia en los patrones de diversidad. Ver Figura\ ref {fig:Coalescent_simulation} para un ejemplo de esto.

La probabilidad de que un par de alelos no hayan podido fusionarse en\(t\) generaciones y luego fusionarse en la\(t+1\) generación posterior es
\[\mathbb{P}(T_2=t+1) = \frac{1}{2N} \left(1- \frac{1}{2N} \right)^{t} \label{eqn:coal_time_dist}\]
Por ejemplo, la probabilidad de que un par de secuencias se fusionen tres generaciones atrás es la probabilidad de que no se fusionen en la generación 1 y 2, que es\(\left(1- \frac{1}{2N} \right) \times \left(1- \frac{1}{2N} \right)\), multiplicada por la probabilidad de que encuentren un ancestro común, es decir, fusionarse, en la tercera generación, lo que sucede con probabilidad\(\frac{1}{2N}\).
De la forma de Ecuación\ ref {eqn:coal_time_dist} podemos ver que el tiempo de coalescencia de nuestro par de alelos es una variable aleatoria distribuida geométricamente, donde está la probabilidad de éxito\(p=\frac{1}{2N}\). El tiempo de espera para que un par de linajes se fusione es como el número de colas lanzadas mientras se espera una cabeza sobre una moneda con la probabilidad de que una cabeza sea\(\frac{1}{2N}\), es decir, si la población es grande podríamos estar esperando mucho tiempo a que nuestra pareja se fusione. Denotaremos esta distribución geométrica por\(T_2 \sim \text{Geo}(1/(2N))\). El tiempo de coalescencia esperado (es decir, la media sobre muchas repeticiones) de un par de alelos es entonces
\[\mathbb{E}(T_2) = 2N\]
generaciones. Esta forma a la expectativa se desprende del hecho de que la media de una variable aleatoria geométrica es\(\frac{1}{p}\).
Condicional a que un par de alelos se fusionen hace\(t\) generaciones, hay\(2t\) generaciones en las que podría ocurrir una mutación. Ver Figura\ ref {fig:pair_coal_muts} para un ejemplo. Si la tasa de mutación por generación es\(\mu\), entonces el número esperado de mutaciones entre un par de alelos que se fusionaron hace\(t\) generaciones es\(2 t\mu\) (los alelos han pasado por un total de\(2t\) meiosis desde la última vez que compartieron un común ancestro).
[fig:pair_coal_muts]
Así podemos escribir el número esperado de mutaciones (\(S_2\)) separando dos alelos dibujados al azar de la población como
\[\begin{aligned} \mathbb{E}(S_2) &= \sum_{t=0}^{\infty} \mathbb{E}(S_2 | T_2=t) P(T_2=t) \nonumber\\ & =\sum_{t=0}^{\infty} 2 \mu t P(T_2=t) \nonumber\\ & =2\mu \mathbb{E}(T_2) \nonumber\\ & = 4 \mu N \end{aligned}\]
esto hace uso de la ley de expectativa total (ver Apéndice Ecuación\ ref {eqn:tot_exptation_def}) para promediar en qué generación se unen nuestro par de secuencias. Supondremos que la mutación es lo suficientemente rara como para que nunca ocurra en el mismo par de bases dos veces, es decir, no hay múltiples aciertos, de tal manera que podemos ver todos los eventos de mutación que separan nuestro par de secuencias. Esta es la suposición de que la mutación repetida es muy rara en un par de bases se llama la suposición i nfinitamente de muchos sitios, que debería contener si\(N\mu_{BP} \ll 1\), dónde\(\mu_{BP}\) está la tasa de mutación por par de bases. Así, el número de mutaciones entre un par de sitios es el número observado de diferencias entre un par de secuencias. En el capítulo anterior denotamos el número observado de diferencias por pares en sitios putativamente neutros que separan un par de secuencias como\(\pi\) (generalmente lo promediamos sobre varios pares de secuencias para una región). Por lo tanto, bajo nuestro modelo simple, neutral y constante población-tamaño esperamos
\[\mathbb{E}(\pi) = 4 N \mu = \theta \label{eqn:pi_expectation}\]
Entonces podemos obtener una estimación empírica\(\theta\) de\(\pi\), llamémoslo\(\widehat{\theta}_{\pi}\), estableciendo, es decir\(\widehat{\theta}_{\pi}=\pi\), nuestro nivel observado de diversidad genética por pares. Si tenemos una estimación independiente de\(\mu\), entonces a partir del ajuste\(\pi =\widehat{\theta}_{\pi} = 4N\mu\) podemos obtener además una estimación del tamaño de la población\(N\) que sea consistente con nuestros niveles de polimorfismo neutro. Si estimamos el tamaño de la población de esta manera, deberíamos llamarlo el tamaño efectivo de la población coalescente (\(N_e\)). Es mejor pensar en el\(N_{e}\) estimado a partir de la diversidad neutra como un tamaño poblacional efectivo a largo plazo para la especie, pero hay muchas advertencias que vienen junto con esa suposición. Por ejemplo, los cuellos de botella pasados y las expansiones poblacionales están todos subsumidos en un solo número y por lo que esta estimación\(N_{e}\) puede no ser muy representativa del tamaño de la población en ningún momento. Dicho esto, no es un mal lugar para comenzar cuando se piensa en la tasa de deriva genética para la diversidad neutra en nuestra población durante largos periodos de tiempo.
Tomemos un momento para distinguir nuestra heterocigosidad esperada (Ecuación\ ref {eqn:hetero}) de nuestro número esperado de diferencias por pares (\(\pi\)). Nuestra heterocigosidad esperada es la probabilidad de que dos alelos en un locus, muestreados de una población al azar, sean diferentes entre sí. Si se han producido una o más mutaciones desde la última vez que un par de alelos compartieron un ancestro común, entonces nuestras secuencias serán diferentes entre sí. Por otro lado, nuestra\(\pi\) medida realiza un seguimiento del número total promedio de diferencias entre nuestros loci. Como tal, a menudo\(\pi\) es una medida más útil, ya que registra el número de diferencias entre las secuencias, no solo si son diferentes entre sí (sin embargo, para ciertos tipos de loci, por ejemplo, microsatélites, a menudo se usa heterocigosidad ya que generalmente no podemos contar hasta el mínimo número de mutaciones de una manera sensible). En el caso de que nuestro locus sea un solo par de bases, las dos medidas generalmente estarán cerca una de la otra, como\(H \approx \theta\) para valores pequeños de\(\theta\). Por ejemplo, comparar dos secuencias al azar en humanos,\(\pi \approx 1/1000\) por par de bases, y la probabilidad de que un par de bases específico difiera entre dos secuencias es\(\approx 1/1000\). Sin embargo, estas dos cantidades comienzan a diferir entre sí cuando consideramos regiones con mayores tasas de mutación. Por ejemplo, si consideramos una región de 10kb, nuestra tasa de mutación será 10,000 veces mayor que un solo par de bases. Para esta longitud de secuencia la probabilidad de que dos haplotipos elegidos aleatoriamente difieran es bastante diferente del número de diferencias mutacionales entre ellos. (Pruebe una tasa de mutación\(10^{-8}\) por base y un tamaño de población de\(10,000\) en nuestros cálculos de\(\E[\pi]\) y H para ver esto.)

Robinson encontró que el zorro californiano en peligro de extinción de la Isla del Canal en San Nicolás había
encontrado muy bien que el zorro californiano de la Isla del Canal en peligro de extinción en San Nicolás tenía niveles muy bajos de diversidad (\(\pi =0.000014 \text{bp}^{-1}\)) en comparación con su pariente cercano el zorro gris continental de California ( \(0.0012\text{bp}^{-1}\)).
- Suponiendo una tasa de mutación\(2\times 10^{-8}\) por pb, ¿qué tamaños efectivos de población estima para estas dos poblaciones?
- ¿Por qué es tan bajo el tamaño efectivo de la población del zorro de Channel Island? [Pista: rápidamente google zorros de la isla del canal para leer sobre su historia, también para ver lo ridículamente lindos que son.]
En sus propias palabras describa por qué el tiempo de coalescencia de un par de linajes escala linealmente con el tamaño de la población (efectiva).
Más detalles sobre la coalescencia por pares y la aleatoriedad de la mutación
Encontramos que nuestros tiempos de coalescencia por pares siguieron una distribución geométrica, Ecuación\ ref {eqn:coal_time_dist}. Sin embargo, eso supone generaciones discretas, y a menudo vamos a pensar en poblaciones que carecen de generaciones discretas (es decir, individuos que se reproducen en momentos aleatorios con algún tiempo medio de generación). Usando nuestra aproximación exponencial, podemos ver que es
\[\approx \frac{1}{2N} e^{-t/(2N)}\]
y así pensar en una variable aleatoria continua, es decir, podríamos decir que el tiempo de coalescencia de un par de secuencias (\(T_2\)) se distribuye aproximadamente exponencialmente con una tasa\(1/(2N)\), i.e\(T_2 \sim \text{Exp}\left( 1/(2N) \right)\). Formalmente podemos hacer esto tomando el límite del proceso discreto con más cuidado. Consulte la Ecuación del Apéndice\ ref {eqn:exp_rv_def} para obtener más información sobre las variables aleatorias exponenciales.
Hemos derivado el número esperado de diferencias entre un par de secuencias y hablado sobre la variabilidad del tiempo de coalescencia para un par de secuencias. El proceso de mutación también es muy variable; aunque dos secuencias se fusionen en un pasado muy lejano por casualidad, aún pueden ser idénticas en el presente si no hubo mutación durante ese tiempo.
Condicional al tiempo de coalescencia\(t\), la probabilidad de que nuestro par de alelos esté separado por\(S_2\) mutaciones desde la última vez que compartieron un ancestro común se distribuye bionomialmente
\[\mathbb{P}(S_2 | T_2 = t ) = {2t \choose j} \mu^{j} (1-\mu)^{2t-j}\]
es decir, las mutaciones ocurren en\(j\) generaciones y no ocurren en\(2t-j\) generaciones (con\({2t \choose j}\) formas en que esta combinación de eventos puede ocurrir posiblemente). Ver Apéndice Ecuación\ ref {eqn:binomial_dist} para la discusión de la distribución binomial. Suponiendo eso\(\mu \ll 1\) y\(2t-j \approx 2t\) aquello, entonces podemos aproximar la probabilidad de que tengamos\(S_2\) mutaciones como una distribución de Poisson:
\[\mathbb{P}(S_2 | T_2 = t ) = \frac{ (2 \mu t )^{j} e^{-2\mu t}}{j!}\]
es decir, un Poisson con media\(2\mu t\). Este es un ejemplo de llevar la distribución binomial a su límite de distribución de Poisson, ver Apéndice Ecuación\ ref {eqn:bionom_to_poiss} para más detalles. No vamos a hacer mucho uso de este resultado, pero es muy útil para pensar en cómo simular el proceso de mutación.
El proceso de coalescencia de una muestra de alelos.
Por lo general, no solo nos interesan los pares de alelos, o la diversidad promedio por pares. Generalmente nos interesan las propiedades de la diversidad en muestras de una serie de alelos extraídos de la población. En lugar de simplemente seguir un par de linajes de regreso hasta que se fusionen, podemos seguir la historia de una muestra de alelos de regreso a través de la población.
Considera primero muestrear tres alelos al azar de la población. La probabilidad de que los tres alelos elijan exactamente el mismo alelo ancestral una generación atrás es\(\frac{1}{(2N)^2}\). Si\(N\) es razonablemente grande, entonces esta es una probabilidad muy pequeña. Como tal, es muy poco probable que nuestros tres alelos se unan todos a la vez, y en un momento veremos que es seguro ignorar eventos tan improbables.

La probabilidad de que un par específico de alelos encuentre un ancestro común en la generación anterior sigue siendo\(\frac{1}{(2N)}\). Hay tres pares posibles de alelos, por lo que la probabilidad de que ningún par encuentre un ancestro común en la generación anterior es
\[\left(1-\frac{1}{2N} \right)^3 \approx \left( 1- \frac{3}{2N} \right)\]
Al hacer esta aproximación estamos multiplicando el lado derecho e ignorando términos de\(1/N^2\) y superior (una aproximación de Taylor, ver Ecuación Apéndice\ ref {EQN:Taylor_exp}). Ver Figura\ ref {fig:Coalescent_simulation_3} para una realización aleatoria de este proceso.
De manera más general, cuando se toman muestras de\(i\) alelos hay\({i \choose 2}\) pares, es decir,\(i(i-1)/2\) pares. Así, la probabilidad de que ningún par de alelos en una muestra de tamaño\(i\) se fusione en la generación anterior es
\[\left(1-\frac{1}{(2N)} \right)^{i \choose 2} \approx \left( 1- \frac{i \choose 2}{2N}\right)\]
mientras que la probabilidad de que cualquier par se\(\approx \frac{i \choose 2}{2N}\) fusione es, nuevamente usando la Ecuación\ ref {EQN:Taylor_exp}.
Podemos ignorar la posibilidad de que más de pares de alelos (por ejemplo, tripletones) se fusionen simultáneamente a la vez, ya que los términos de\(\frac{1}{N^2}\) y superiores pueden ignorarse ya que son increíblemente raros. Obviamente en tamaños de muestra razonables hay muchas más combinaciones triples (\({i \choose 3}\)) y de orden superior que pares (\({i \choose 2}\)), pero si\(i \ll N\) entonces estamos seguros de ignorar estos términos.
Cuando hay\(i\) alelos, la probabilidad de que esperemos hasta la\(t+1\) generación antes de que cualquier par de alelos se fusione es
\[\mathbb{P}(T_i =t+1) = \frac{i \choose 2}{2N}\left( 1- \frac{i \choose 2}{2N}\right)^{t} \label{eqn:T_i}\]
Así, el tiempo de espera hasta el primer evento coalescente mientras hay\(i\) linajes es una variable aleatoria distribuida geométricamente con probabilidad de éxito\(p=\frac{i \choose 2}{2N}\), que denotamos por
\[T_i \sim \text{Geo} \left( \frac{i \choose 2}{2N} \right).\]
El tiempo medio de espera hasta que cualquiera de los pares dentro de nuestra muestra se coalesce es
\[\mathbb{E}( T_i) = \frac{2N}{i \choose 2} \label{eqn:E_T_i}\]
que de nuevo se desprende de la media de una variable aleatoria geométrica siendo\(\frac{1}{p}\).
Después de que un par de alelos encuentra por primera vez un alelo ancestral común algunas generaciones atrás en el pasado, solo tenemos que hacer un seguimiento de ese alelo ancestral común para la pareja al mirar más al pasado. En nuestro ejemplo genealogía coalescente para nuestros 3 alelos, mostrada en la Figura\ ref {fig:Coalescent_simulation_3}, comenzamos por rastrear los 3 linajes, luego por casualidad los azules y morados se fusionan en las cuatro generaciones atrás. Entonces estamos rastreando solo dos linajes, el linaje rojo y el linaje ancestral de los alelos azules y morados; luego esos dos se fusionan y hemos encontrado a nuestro ancestro común más reciente de nuestra muestra. Otro ejemplo con cuatro puntas se muestra en la Figura\ ref {fig:coal_w_muts}; estamos rastreando cuatro linajes, luego un par se fusionan, luego rastreamos tres linajes, luego un par se fusionan, luego estamos rastreando dos linajes, luego este par final se fusiona y hemos encontrado el ancestro común más reciente de nuestra muestra (fin, fin escena).
De manera más general, cuando un par de alelos en nuestra muestra de\(i\) alelos se fusiona, luego cambiamos a tener que seguir\(i-1\) alelos atrás en el tiempo. Entonces cuando un par de estos\(i-1\) alelos se fusionan, entonces sólo tenemos que seguir\(i-2\) alelos hacia atrás. Este proceso continúa hasta unirnos de nuevo a una muestra de dos, y de ahí a un solo ancestro común más reciente (MRCA).
Para simular una genealogía coalescente en un locus para una muestra de\(n\) alelos, simplemente seguimos el siguiente algoritmo:
- Set\(i=n\).
- Simular una variable aleatoria para que sea el tiempo\(T_i\) hasta el siguiente evento coalescente de\(T_i \sim \text{Exp}\left(\frac{i \choose 2}{2N} \right)\)
- Elija un par de alelos para fusionar al azar de todos los pares posibles.
- Set\(i=i-1\)
- Continuar looping pasos 2-4 hasta que\(i=1\), es decir, se encuentre el ancestro común más reciente de la muestra.
Siguiendo este algoritmo estamos generando realizaciones de la genealogía de nuestra muestra.
Propiedades esperadas de genealogías y mutaciones coalescentes

El tiempo esperado para el ancestro común más reciente.
Primero consideraremos el tiempo al ancestro común más reciente de toda la muestra (\(T_{MRCA}\)). Esto es
\[T_{MRCA} = \sum_{i=n}^2 T_i\]
generaciones atrás, donde estamos sumando desde\(i=n\) alelos contando hacia atrás hasta\(i=2\) alelos (ver Figura\ ref {fig:coal_w_muts} por ejemplo). Como nuestros tiempos de coalescencia para diferentes\(i\) son independientes, el tiempo esperado para el ancestro común más reciente es
\[\mathbb{E}(T_{MRCA}) = \sum_{i=n}^2 \mathbb{E}(T_i) = \sum_{i=n}^2 2N/{i \choose 2}\]
Usando el hecho de que\(\frac{1}{i(i-1)}=\frac{1}{i-1} - \frac{1}{i}\) y un poco de reordenamiento, podemos reescribir esto como
\[\mathbb{E}(T_{MRCA}) = 4N\left(1- \frac{1}{n} \right) \label{TMRCA_neutral}\]
Por lo que el promedio\(T_{MRCA}\) escala linealmente con el tamaño de la población\(N\). Curiosamente, a medida que avanzamos hacia muestras cada vez más grandes (es decir\(n \gg 1\)), el tiempo promedio hasta el ancestro común más reciente converge en\(4N\). Lo que sucede aquí es que en muestras grandes nuestros linajes suelen fusionarse rápidamente al principio y muy pronto se fusionan hasta llegar a un número mucho menor de linajes.
Asumir una población autosómica efectiva de 10,000 individuos (aproximadamente la estimación humana a largo plazo) y un tiempo de generación de 30 años. ¿Cuál es el tiempo esperado para el ancestro común más reciente de una muestra de 20 personas? ¿Cuál es este momento para una muestra de 500 personas?
El tiempo total esperado en una genealogía y el número de sitios segregantes.
Las mutaciones caen en linajes específicos de la genealogía coalescente y se transmiten a todos los descendientes de su linaje. Además, bajo la suposición infinitamente de muchos sitios, cada mutación crea un nuevo sitio de segregación. El proceso de mutación es un proceso de Poisson, y cuanto más largo sea un linaje particular, es decir, cuantas más generaciones de meiosis representa, más mutaciones se pueden acumular en él. El número total de sitios segregantes en una muestra es así una función de la cantidad total de tiempo en la genealogía de la muestra, o la suma de todas las longitudes de rama en el árbol genealógico,\(T_{tot}\). Nuestra cantidad total de tiempo en la genealogía es
\[T_{tot} = \sum_{i=n}^2 iT_i\]
como cuando hay\(i\) linajes, cada uno aporta un tiempo\(T_i\) al tiempo total (ver Figura\ ref {fig:carbón_w_muts} para un ejemplo). Tomando la expectativa del tiempo total en la genealogía,
\[\mathbb{E}(T_{tot}) = \sum_{i=n}^2 i \frac{2N}{{i \choose 2} } = \sum_{i=n}^2 \frac{4N}{i -1} =\sum_{i=n-1}^1 \frac{4N}{i} \label{eqn:E_T_tot}\]
vemos que nuestra cantidad de tiempo total esperada en la genealogía escala linealmente con el tamaño de nuestra población\(N\). Nuestra cantidad de tiempo total esperada también está aumentando con el tamaño de la muestra\(n\), pero lo está haciendo muy lentamente. Esto se deduce nuevamente del hecho de que en muestras grandes, la coalescencia inicial suele ocurrir muy rápidamente, por lo que las muestras adicionales agregan poco a la cantidad total de tiempo en el árbol genealógico. Vimos anteriormente que el número de diferencias mutacionales entre un par de alelos que coalescencia hace\(T_2\) generaciones fue Poisson con una media de\(2 \mu T_2\), donde\(2T_{2}\) está la longitud total de la rama en este simple árbol genealógico de 2 muestras. Una mutación que ocurre en cualquier rama de nuestra genealogía provocará un polimorfismo segregante en la muestra (cumpliendo con nuestro supuesto infinitamente de muchos sitios). Así, si el tiempo total en la genealogía lo es\(T_{tot}\), hay\(T_{tot}\) generaciones para mutaciones. Entonces el número total de mutaciones que segregan en nuestra muestra (\(S\)) es Poisson con media\(\mu T_{tot}\). Así, el número esperado de sitios segregantes en una muestra de tamaño\(n\) es
\[\mathbb{E}(S) = \mu \mathbb{E}(T_{tot}) = \sum_{i=n-1}^1 \frac{4N\mu }{i} = \theta \sum_{i=n-1}^1 \frac{1}{i} \label{eqn:seg_sites}\]
Obsérvese que esta está creciendo con el tamaño de la muestra\(n\), aunque muy lentamente (aproximadamente a la velocidad\(\log\) del tamaño de la muestra). Podemos usar esta fórmula para derivar otra estimación de la tasa de mutación escalada poblacional\(\theta\), estableciendo nuestro número observado de sitios segregantes en una muestra (\(S\)) igual a esta expectativa. Llamaremos a este estimador\(\widehat{\theta}_W\):
\[\widehat{\theta}_W =\frac{ S}{\sum_{i=n-1}^1 \frac{1}{i}} \label{watterson_theta}\]
Este estimador de\(\theta\) fue ideado por, de ahí el\(W\).
El espectro de frecuencia de sitio neutro
Podemos usar nuestro proceso de coalescencia para encontrar el número esperado de alelos derivados presentes\(i\) tiempos de un tamaño de muestra\(n\), por ejemplo, ¿cuántos singletons (\(i = 1\)) esperamos encontrar en nuestra muestra? Por ejemplo, en la Figura\ ref {fig:coal_w_muts} en nuestra muestra de cuatro secuencias, hay 3 singletones y 2 dobletones. El número de sitios con estas diferentes frecuencias alélicas depende de la longitud de ramas genealógicas específicas. Una mutación que cae sobre una rama con\(i\) descendientes creará un alelo derivado con frecuencia\(i\). Por ejemplo, en nuestro árbol de ejemplo en la Figura\ ref {fig:carbón_w_muts}, el número total de generaciones donde podría surgir una mutación y ser un doblete es\(T_3+2T_2\), la longitud total de la rama ancestral a solo el alelo naranja y rojo\((T_3+T_2)\) más la rama ancestral a solo la alelo azul y morado\((T_2)\).
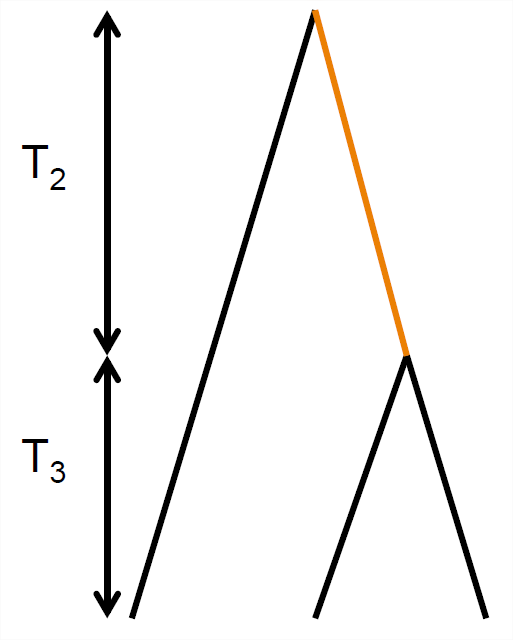
Para ver cómo podríamos resolver esto, comencemos considerando el simple árbol coalescente, que se muestra en la Figura\ ref {fig:freq_coal}, para muestra de\(3\) alelos extraídos de una población. Las mutaciones que caen sobre las ramas coloreadas en negro se derivarán singletones, mientras que las mutaciones que caen a lo largo de la rama naranja serán dobletones en la muestra. El número total de generaciones donde podría surgir una mutación singleton es\(3 T_3 + T_2\). Tenga en cuenta que solo contamos el tiempo donde hay dos linajes\((T_{2})\) una vez. Así que nuestro número esperado de singletons, usando la ecuación\ ref {eqn:e_t_i}, es
\[\mathbb{E}(S_i) = \mu \left( 3\mathbb{E}(T_3) + \mathbb{E}(T_2) \right) = \mu \left( 3 \frac{2N}{3}+ 2N \right) = \theta\]
Por lógica similar, el tiempo donde podrían surgir dobletones es\(T_2\) y nuestro número esperado de dobletones es\(\mathbb{E}(S_i) =\theta/2\). Así, hay en promedio la mitad de dobletones que los singletones.
Extender esta lógica a muestras más grandes podría ser factible, pero es tedioso (quiero decir, realmente tedioso: para 10 alelos hay miles de formas de árbol posibles y la tarea rápidamente se vuelve imposible incluso computacionalmente). Una prueba agradable y relativamente simple del espectro de frecuencia neutral del sitio viene dada por, pero no vamos a dar esto aquí. La forma general es:
\[\mathbb{E}(S_i) = \frac{\theta }{i} \label{eqn:neutral_freq_spec}\]
es decir, hay el doble de singletones que dobletones, tres veces más singletones que tripletones, y así sucesivamente. La otra cosa que nos será útil saber es que los alelos neutros a frecuencia intermedia tienden a ser viejos, y los que son raros en la muestra son en promedio jóvenes. Esperamos ver muchos más alelos raros en nuestra muestra que alelos comunes.
Hay dos posibles formas de árboles que podrían relacionar cuatro muestras. Dibuje ambos y coloree por separado (o marque de otro modo) las ramas por donde podrían surgir alelos derivados de singletones, dobletones y tripletes.
También podemos preguntar la probabilidad de observar un alelo derivado segregándose en frecuencia\(i/n\) dado que el sitio es polimórfico en nuestra muestra de tamaño\(n\) (es decir, dado eso\(0<i<n\)). Podemos obtener esta probabilidad dividiendo el número esperado de sitios que segregan para un alelo a frecuencia\(i\) por el número esperado que segrega en todas las frecuencias alélicas posibles para polimorfismos en nuestra muestra
\[\begin{aligned} \mathbb{P}(i |0<i<n) &=\frac{\mathbb{E}(S_i)}{\sum_{j=1}^{n-1} \mathbb{E}(S_j)} = \frac{\frac{1}{i}}{\sum_{j=1}^{n-1} \frac{1}{j}}.\end{aligned}\]
Podemos interpretar esta probabilidad como la fracción de sitios polimórficos que esperamos encontrar con una frecuencia\(i/n\).
Pruebas basadas en el espectro de frecuencias del sitio
Los genetistas poblacionales han propuesto una variedad de formas de probar si un espectro de frecuencia de sitio observado se ajusta a sus expectativas neutras y de tamaño constante. Estas pruebas son útiles para detectar cambios en el tamaño de la población usando datos en muchos loci, o para detectar la señal de selección en loci individuales. Una de las primeras pruebas fue propuesta por, y se llama Tajima's\(D\). Tajima\(D\) es
\[D = \frac{\hat{\theta}_{\pi}-\hat{\theta}_{W}}{C} \label{eqn_Tajimas_D}\]
donde el numerador es la diferencia entre la estimación de\(\theta\) basada en diferencias por pares y la basada en sitios de segregación. Como estos dos estimadores ambos tienen expectativa\(\theta\) bajo el modelo neutral, de tamaño constante, la expectativa de\(D\) es cero. El denominador\(C\) es una constante positiva; es la raíz cuadrada de un estimador de la varianza de esta diferencia bajo el tamaño constante de la población, modelo neutro. Esta constante se eligió\(D\) para tener media cero y varianza\(1\) bajo el modelo nulo, por lo que podemos probar las salidas de este modelo nulo simple.
Un exceso de alelos raros en comparación con el modelo neutro de tamaño constante dará como resultado un Tajima negativo\(D\), ya que cada alelo raro adicional aumenta el número de sitios de segregación en\(1\), pero solo tiene un pequeño efecto en el número de diferencias por pares entre muestras. En contraste, un Tajima positivo\(D\) refleja un exceso de alelos de frecuencia intermedia en relación con la expectativa neutra de tamaño constante. Los alelos a frecuencia intermedia aumentan la diversidad por pares más por sitio de segregación de lo típico, aumentando así\(\theta_{\pi}\) más de\(\theta_{W}\). En la siguiente sección veremos cómo los cambios a largo plazo en el tamaño de la población cambian sistemáticamente el espectro de frecuencias del sitio y así son detectables por estadísticas como las de Tajima\(D\).
Demografía y la coalescencia
Ya hemos visto cómo los cambios en el tamaño de la población pueden cambiar la velocidad a la que se pierde la heterocigosidad de la población (ver la discusión en torno a la Ecuación\ ref {eqn:var_pop_coal}). Si el tamaño de la población en generación\(i\) es\(N_i\), la probabilidad de que un par de linajes se fusionen es\(\frac{1}{(2N_i)}\); esto se ajusta a nuestra intuición de que si el tamaño de la población es pequeño, la tasa a la que pares de linajes encuentran a su ancestro común es más rápida. Potencialmente podemos acomodar fluctuaciones aleatorias rápidas en el tamaño de la población simplemente usando el tamaño efectivo de la población\(N_e\) en lugar de\(N\). Sin embargo, cambios más sistemáticos y a largo plazo en el tamaño de la población distorsionarán las genealogías coalescentes, y por lo tanto los patrones de diversidad, de manera más sistemática.

Podemos ver cómo la demografía distorsiona potencialmente el espectro de frecuencias observado alejándose de la expectativa neutra en una muestra muy grande de humanos mostrada en la Figura\ ref {fig:Human_growth}. A modo de comparación, el espectro de frecuencia neutra, Ecuación\ ref {eqn:neutral_freq_spec}, se muestra como una línea roja. Hay alelos mucho más raros de lo esperado bajo nuestro modelo neutral, de tamaño constante, pero la predicción neutra y la realidad coinciden algo más para los alelos que son más comunes.

¿Por qué es esto? Pues bien, estos patrones son probablemente el resultado del crecimiento explosivo muy reciente de las poblaciones humanas. Si la población ha crecido rápidamente, entonces la tasa de coalescencia por parejas en el pasado puede ser mucho mayor que la tasa de coalescencia más cercana al presente. (ver Figura\ ref {fig:Genealogy_Growth}).
Una consecuencia de una reciente expansión poblacional es que hay mucha menos diversidad genética en la población de lo que se podría predecir usando el tamaño de la población censal. Los humanos son un ejemplo de este efecto; hoy somos\(7\) mil millones de nosotros vivos, pero esto se debe al crecimiento demográfico muy rápido en los últimos mil a decenas de miles de años. Nuestro nivel de diversidad genética es mucho más bajo de lo que usted predeciría dado el tamaño de nuestro censo, reflejando nuestra población ancestral mucho más pequeña. Una segunda consecuencia de la reciente expansión poblacional es que las ramas coalescentes más profundas están mucho más aplastadas en el tiempo en comparación con las de una población de tamaño constante. Las mutaciones en ramas más profundas son la fuente de alelos a frecuencias más intermedias, por lo que hay aún menos alelos de frecuencia intermedia en poblaciones en crecimiento. Por eso hay tantos alelos raros, especialmente singletons, en esta gran muestra de europeos.
Otro escenario demográfico común es un cuello de botella poblacional. En un cuello de botella, el tamaño de la población se desploma dramáticamente, y posteriormente se recupera. Por ejemplo, nuestra población pudo haber tenido tamaño\(N_{\textrm{Big}}\) y se estrelló hasta\(N_{\textrm{Small}}\). Un ejemplo de cuello de botella se muestra en la Figura\ ref {fig:Genealogy_crash}.

Al observar una muestra de linajes extraídos de la población actual, si el cuello de botella fue algo reciente (\(\ll N_{\textrm{Big}}\)generaciones en el pasado) muchos de nuestros linajes no se habrán unido antes de llegar al cuello de botella, retrocediendo en el tiempo. Pero durante el cuello de botella nuestros linajes se fusionan a un ritmo mucho mayor, tal que muchos de nuestros linajes se fusionarán si el cuello de botella dura lo suficiente (\(\sim N_{\textrm{Small}}\)generaciones). Si el cuello de botella es muy fuerte, entonces todos nuestros linajes se fusionarán durante el cuello de botella, y el espectro de frecuencia del sitio resultante puede parecerse mucho a nuestro modelo de crecimiento poblacional (es decir, un exceso de alelos raros). Sin embargo, si algunos pares de linajes escapan a la fusión durante el cuello de botella, se unirán mucho más profundamente en el tiempo (por ejemplo, los linajes ancestrales azul y naranja en\ ref {fig:Genealogy_crash}).
Un ejemplo de esto se muestra Figura\ ref {fig:mimulus_bottleneck}, datos de. Mimulus nasutus es una especie autofecundante que surgió recientemente de un progenitor externo M. guttatus y experimentó un fuerte cuello de botella. M. guttatus tiene niveles muy altos de diversidad genética (\(\pi=4\%\)en sitios sinónimos), pero M. nasutus ha perdido gran parte de esta diversidad (\(\pi =1\%\)). Mirando a lo largo del genoma, entre un par de cromosomas de M. guttatus, los niveles de diversidad son bastante altos de manera uniforme.

Pero al comparar dos cromosomas de M. nasutus, la diversidad es baja porque el par de linajes generalmente se fusionan recientemente. Sin embargo, en algunos lugares vemos niveles de diversidad comparables a M. guttatus; estas regiones corresponden a sitios genómicos donde nuestro par de linajes no logran fusionarse durante el cuello de botella y posteriormente fusionarse mucho más profundamente en el ancestral M. guttatus población.


Las mutaciones que surjan en linajes más profundos estarán a frecuencia intermedia en nuestra muestra, por lo que los cuellos de botella leves pueden conducir a un exceso de alelos de frecuencia intermedia en comparación con el modelo estándar de tamaño constante. Esto puede sesgar la D de Tajima (ver Ecuación\ ref {EQN_Tajimas_D}) hacia valores positivos y alejándose de su expectativa de cero. Un ejemplo de este sesgo se muestra en la Figura\ ref {fig:Maize_Tajimas_D}. Maíz (Zea mays subsp. mays) fue domesticado a partir de su progenitor silvestre teosinte (Zea mays subsp. parviglumis) hace aproximadamente diez mil años. Podemos ver cómo el cuello de botella asociado a la domesticación ha dado como resultado una pérdida de diversidad genética en el maíz en comparación con el teosinte, y el polimorfismo que permanece está algo sesgado hacia frecuencias intermedias dando como resultado valores más positivos de la D. de Tajima.
Voight et al. (2005) secuenciaron 40 regiones autosómicas de 15 muestras diploides de personas hausa de Yaundé, Camerún. La longitud promedio del locus que secuenciaron para cada región fue\(2365\) pb. Encontraron que el promedio de sitios segregantes por locus fue\(S= 11.1\) y el promedio\(\pi = 0.0011\) por base sobre los loci. ¿La D de Tajima es positiva o negativa? Es un modelo demográfico con un cuello de botella o crecimiento más consistente con este resultado
Resumen
- La deriva genética es el cambio aleatorio en las frecuencias alélicas debido a que los alelos por casualidad dejan más o menos copias de sí mismos a la siguiente generación. Es sin dirección, con alelos igualmente propensos a subir o bajar en frecuencia gracias a la deriva. La deriva genética ocurre a un ritmo más lento en poblaciones más grandes, ya que hay un mayor grado de promedio en poblaciones más grandes que reduce el impacto de la aleatoriedad en la reproducción de los individuos.
- En promedio, la deriva genética actúa para eliminar la diversidad genética (por ejemplo, heterocigosidad) de la población. La tasa a la que se pierde diversidad genética neutra de la población es inversamente proporcional al tamaño de la población.
- Un equilibrio de mutación y deriva genética puede mantener un nivel de equilibrio de diversidad genética neutra en una población. Este nivel de equilibrio está determinado por la tasa de mutación a escala poblacional (\(N \mu\)).
- En la práctica, la deriva genética rara vez se producirá a la tasa sugerida por el tamaño de la población censal, por ejemplo, debido a una gran varianza en el éxito reproductivo y las fluctuaciones de tamaño En muchas situaciones, podemos abordar esto utilizando un tamaño de población efectivo en lugar del tamaño de la población censal. Podemos estimar este tamaño poblacional efectivo haciendo coincidir nuestra tasa observada de deriva genética con la esperada en una población idealizada.
- Una visión clave al pensar en los patrones de diversidad neutra es darse cuenta de que las mutaciones neutras no alteran la forma del árbol genético (o genealogía) que relaciona a los individuos, por lo que a menudo es útil pensar primero en el árbol y luego pensar en mutaciones neutras dispersas en la parte superior de este árbol.
- La teoría coalescente describe las propiedades de estos árboles, y los patrones mutacionales generados, bajo un modelo de evolución neutra.
- Los cambios a largo plazo en el tamaño de la población alteran la tasa de coalescencia de manera predecible que impacta patrones de variación. Estos patrones pueden ser utilizados para detectar violaciones de un modelo poblacional constante y para estimar modelos demográficos más complejos.
Con base en muestras de museos de\(\sim 1800\), estima que la heterocigosidad promedio en los elefantes marinos del norte fue\(0.0304\) en muchos loci. Con base en más muestras, se estima que en\(1960\) este había bajado a\(0.011\). Los elefantes marinos tienen un tiempo de generación de\(8\) años.
¿Qué tamaño efectivo de población estima que es consistente con esta caída?
- ¿Por qué se espera que grandes poblaciones alberguen una variación más neutra?
- ¿Cuál es el tamaño efectivo de la población? ¿Suele ser mayor o menor que el tamaño de la población censal?
- ¿Por qué el tamaño efectivo de la población difiere entre los autosomas, el cromosoma Y y el ADNmt?
Secuencias una región genómica de una especie de babuino. De 100 mil pares de bases, en promedio, 200 difieren entre cada par de secuencias. Asumir una tasa de mutación por base de\(1 \times 10^{-8}\) y un tiempo de generación de diez años.
- ¿Cuál es el tamaño poblacional efectivo de estos babuinos?
- ¿Cuál es el tiempo promedio de coalescencia (en años) de un par de secuencias en esta especie?


