9: La respuesta de múltiples rasgos a la selección
- Page ID
- 58133
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La aptitud de un organismo depende del resultado de muchos procesos y fenotipos diferentes del organismo. Así, la selección natural suele actuar sobre muchos fenotipos en concierto. En algunos casos las diversas direcciones que la selección intenta tirar de los fenotipos de la población puede no ser posible satisfacer todas a la vez. Tales compensaciones de aptitud ocurren cuando la selección actúa sobre fenotipos genéticos correlacionados de manera contradictoria.
Para entender la consecuencia a corto plazo de la selección en múltiples fenotipos podemos generalizar la ecuación del Obtentor a múltiples rasgos. Teniendo en cuenta dos rasgos podemos escribir nuestras respuestas en ambos rasgos como
\[\begin{aligned} R_1 & = V_{A,1} \beta_1 + V_{A,1,2} \beta_2 \nonumber \\[4pt] R_2 & = V_{A,2} \beta_2 + V_{A,1,2} \beta_1 \label{eqn:2D_breeders_eqn} \end{aligned}\]
donde el\(2\) índice\(1\) y nuestros dos rasgos diferentes. Aquí\(V_{A,1}\) y\(V_{A,2}\) están la varianza genética aditiva para rasgo\(1\) y\(2\) respectivamente, mientras que\(V_{A,1,2}\) es nuestra covarianza aditiva entre nuestros rasgos. Nuestro gradiente de selección para el rasgo 1\(\beta_1\),, representa el cambio en la aptitud a medida que cambia el rasgo 1 solo manteniendo constantes otros rasgos. Estos\(\beta\) pueden ser estimados por regresión multivariada, ver más adelante. La ecuación de los criadores multivariados es una afirmación de que nuestra respuesta en cualquier fenotipo se modifica mediante la selección de otros rasgos que genéticamente covarían con ese rasgo.
También podemos escribir esto de manera equivalente en forma de matriz, para un número arbitrario de rasgos. Escribiendo nuestro cambio en la media de nuestros múltiples fenotipos dentro de una generación como vector\(\bf{S}\) y nuestra respuesta a través de múltiples generaciones como vector\(\bf{R}\). Estas dos cantidades están relacionadas por
\[\bf{R} = \bf{G} \bf{V_P}^{-1} \bf{S} = \bf{G} \boldsymbol{ \beta} \label{eqn:MV_breeders_eqn}\]
donde\(\bf{V_P}\) y\(\bf{G}\) son nuestras matrices de la varianza-covarianza de fenotipos y valores genéticos aditivos (Ecuación\ ref {G_Matrix] [P_matrix]}) y\(\boldsymbol{\beta}\) es un vector de gradientes de selección (es decir, el cambio dentro de una generación como una fracción del total varianza fenotípica). Nótese que\(\boldsymbol{\beta} = \bf{V_P}^{-1} \bf{S}\), tal que cada uno\(\beta\) representa el gradiente de selección sobre un rasgo que da cuenta de sus covarianzas fenotípicas con otros rasgos.

Un ejemplo del resultado de la selección en múltiples fenotipos considera el combate de selección medido por el pinzón de Darwin de suelo medio (Geospiza fortis). Midieron 634 aves en el '76, de las cuales solo\(15\%\) sobrevivieron hasta 1977. Las aves que sobrevivieron eran más pesadas y tenían picos más largos y profundos que el promedio.
| Rasgo | Media antes de la selección (1976) | S | \(\beta\) | Media siguiente generación. (1978) |
|---|---|---|---|---|
| Peso | 16.06 | 0.74 | \ (\ beta\) ">0.477 | 17.13 |
| Longitud de Factura | 10.63 | 0.54 | \ (\ beta\) ">-0.144 | 10.95 |
| Profundidad de Factura | 9.21 | 0.36 | \ (\ beta\) ">0.528 | 9.70 |
Teniendo en cuenta las covarianzas fenotípicas entre los rasgos (\(\bf{V_P}^{-1}\)), encontraron que tanto el peso como la profundidad del pico mostraron selección direccional directa hacia valores más grandes (\(\beta\)s positivos). Sin embargo, la longitud del pico mostró una selección débil hacia picos más cortos (negativos\(\beta\)), lo que refleja el hecho de que la longitud del pico muestra correlación fenotípica positiva con la profundidad y el peso del pico, y la mayor parte de la selección directa fue sobre el peso y la profundidad del pico arrastrando la longitud del pico. Al observar la próxima generación, los tres rasgos han aumentado significativamente debido a las fuertes correlaciones genéticas positivas entre los rasgos (Tabla\ ref {Tabla:Geospiza_fortis_VG}). Así, a pesar de que la selección posiblemente favoreció longitudes de pico más cortas, y ciertamente no favoreciendo a los billetes largos, la longitud del pico aumentó en la próxima generación debido a su covarianza genética positiva con dos rasgos que la selección estaba actuando para aumentar.
| Wt | BL | BD | |
|---|---|---|---|
| Wt | 0.85 | ||
| BL | +0.95 | 0.67 | |
| BD | +0.87 | +0.9 | 0.81 |
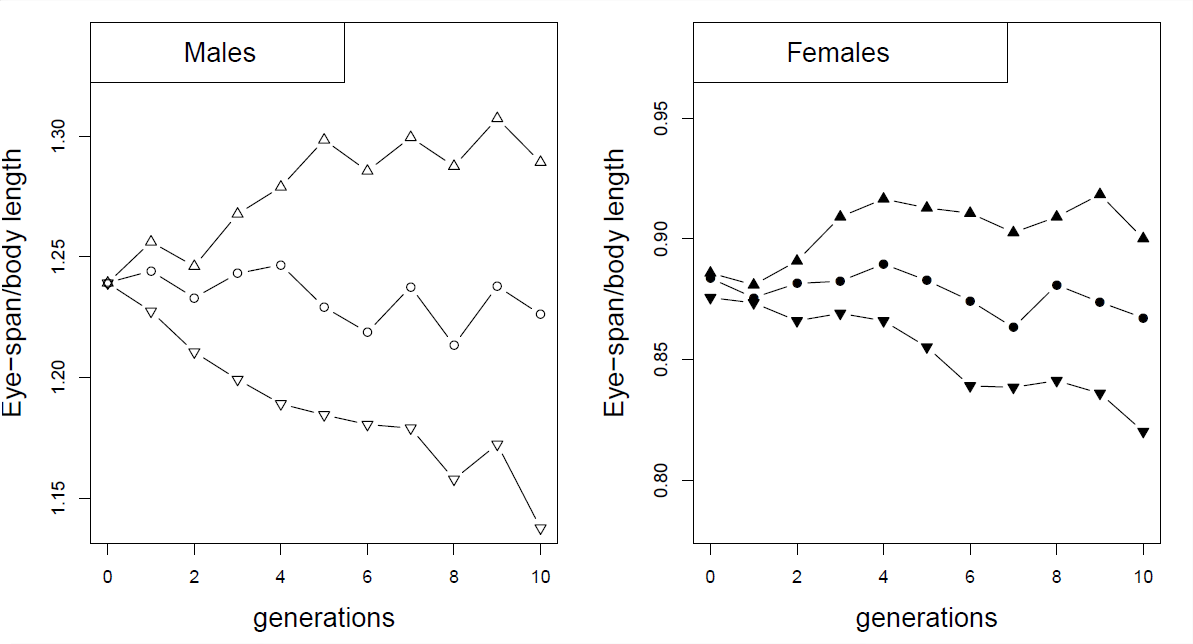
Como ejemplo de respuestas correlacionadas a la selección, considere el experimento de selección en moscas de ojo de tallo (Cyrtodiopsis dalmanni). Las moscas con ojos de tallo han evolucionado asombrosamente largos tallos oculares. En el laboratorio, se establecieron seis poblaciones de moscas capturadas en la naturaleza y se seleccionaron hacia arriba y hacia abajo en los machos la relación entre el tallo ocular y el tamaño corporal durante 10 generaciones (parcela izquierda en la Figura Figura\(\PageIndex{2}\)). A pesar de que no seleccionó en hembras, vio una respuesta correlacionada en las hembras de cada una de las líneas (parcela derecha), debido a la correlación genética entre las proporciones corporales masculinas y femeninas.
_(4561140578).jpg)
Al final de diez generaciones i n eperiment (Figura\(\PageIndex{3}\)), los machos de las líneas seleccionadas hacia arriba y hacia abajo tuvieron proporciones medias de tallo ocular a cuerpo de\(1.29\) y\(1.14\) respectivamente, mientras que las hembras de las líneas seleccionadas hacia arriba y hacia abajo tuvieron medias de \(0.9\)y\(0.82\).
- estimó que cuando seleccionó los 10 machos arriba/abajo, desplazó la relación media corporal en 0.024 en promedio dentro de cada generación (esta es la diferencia entre la media poblacional y la media de los padres en la siguiente generación). ¿Cuál es la heredabilidad masculina de la relación entre el tallo ocular y la longitud del cuerpo?
- Supongamos que la varianza genética aditiva de los fenotipos masculino y femenino es igual y que no hay selección directa sobre la proporción corporal femenina en este experimento, es decir, que toda la respuesta en las hembras se debe a la selección correlacionada. ¿Se puede estimar la correlación genética hombre-mujer de la relación entre el ojo y el tallo?
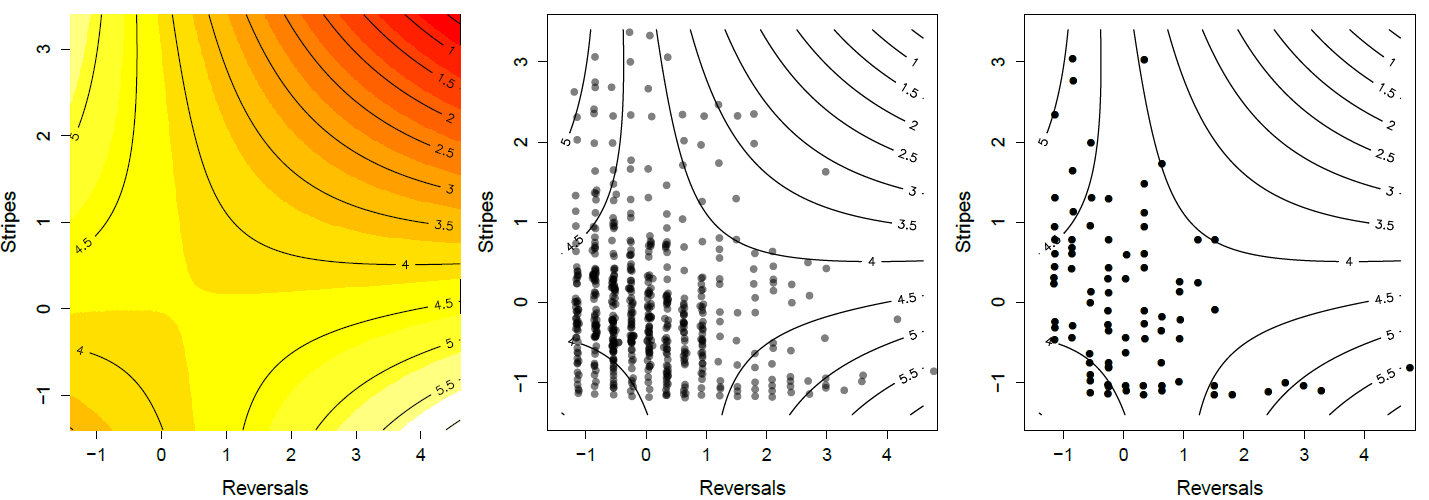
de serpientes supervivientes. Observe cómo las serpientes en la esquina superior izquierda e inferior derecha están sobrerepresentadas en los sobrevivientes. Datos de\ citet {brodie1992correlacional}\ gitcode {https://github.com/cooplab/popgen-no...akes_Brodie.R}.
Estimación de gradientes de selección multivariada
Podemos estimar gradientes de selección multivariados direccionales (\(\beta\)) y cuadráticos (\(\gamma\)) tal como lo hicimos para un solo rasgo (\(x_1\)y\(x_2\)), usando modelos lineales y cuadráticos (en eqn\ ref {fitness_regression} y\ ref {fitness_regression_ puñalada}). Por ejemplo, para dos rasgos podemos escribir
\[w_i \sim \beta_1 x_{1,i} + \frac{1}{2} \gamma_1 x_{1,i}^2 + \beta_2 x_{2,i} + \frac{1}{2} \gamma_2 x_{2,i}^2 + \gamma_{1,2} x_{1,i} x_{2,i} + \bar{w} \label{fitness_regression_MV}\]
donde\(\beta_1\) y\(\gamma_1\) son los gradientes de selección direccionales y cuadráticos para el rasgo uno, y de manera similar para el rasgo dos. El gradiente de selección de covarianza entre rasgos viene dado por\(\gamma_{1,2}\). Esta técnica para medir la selección multivariada a veces se denomina 'regresión Lande-Arnold'.
proporciona un buen ejemplo de selección de múltiples rasgos de prevención de la predación en serpientes liguero del noroeste (Thamnophis ordinoides). liberó a cientos de serpientes nacidas en el laboratorio en la naturaleza, y luego realizó observaciones de marca-recaptura para monitorear su destino. Antes de soltarlas midió lo rayadas que eran, y su tendencia conductual a las inversiones de dirección durante el vuelo simulado de un depredador. Su superficie de aptitud cuadrática se muestra en la Figura\ ref {fig:Garter_serpientes_Brodie}, basada en ajustar la regresión dada por la ecuación\ ref {fitness_regression_MV} a la supervivencia juvenil. Encontró que ni los gradientes direccionales o cuadráticos de un solo rasgo fueron significativos, es decir, no hubo selección aparente de un rasgo ignorando al otro. Sin embargo, hubo una selección significativa de covarianza negativa (\(\gamma_{1,2}<0\)). Los individuos con mayor probabilidad de supervivencia son altamente rayados y realizan pocas reversiones (esquina superior izquierda), o tienen pocas franjas pero inversas frecuentemente (esquina inferior derecha).

Paisajes de fitness multivariantes
En el último capítulo vimos que a menudo podemos pensar en que nuestra población se mueve a través de un panorama de fitness medio. Selección en un solo rasgo correspondiente a nuestra población dando pasos que suben al pico de fitness más cercano. De manera similar, nuestra respuesta de múltiples rasgos a la selección (a menudo) puede considerarse como nuestra población escalando un paisaje medio de acondicionamiento físico (ver Figura\(\PageIndex{6}\)). Sin embargo, el camino que toma nuestra población ahora depende de manera crucial de las correlaciones genéticas.
Anteriormente vimos que nuestro gradiente de selección de rasgo único se puede escribir como\(\beta= \frac{1}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x}}\) (si la aptitud es independiente de la frecuencia,\ ref {eqn:proof_landscape}). Esto se mantiene para cada uno de nuestros rasgos y así podemos reescribir la ecuación de nuestros criadores de dos rasgos (Ecuación\ ref {EQN:2D_breeders_EQN}) como
\[\begin{aligned} R_1 & = \frac{V_{A,1}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_1}} + \frac{ V_{A,1,2}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_2}} \nonumber \\[4pt] R_2 & = \frac{V_{A,2}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_2}} + \frac{ V_{A,1,2}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_1}}\label{eqn:2D_fitness_breeders_eqn}\end{aligned}\]
Si no hay correlación genética aditiva entre los rasgos (\(V_{A,1,2}=0\), panel izquierdo de la Figura\(\PageIndex{6}\)), entonces nuestra población apenas está evolucionando hacia su pico de aptitud local. Lo hace como un escalador demasiado entusiasta que sube por la colina más cercana que encuentra, apenas moviéndose en las partes planas, pero corriendo rápidamente por las partes más empinadas hasta que llega a detenerse en la cima de la colina. Si nuestra población tiene la mala suerte de encontrarse en las laderas de un cerro que no es el pico más alto, nuestra población se adaptará y escalará ese cerro pero no alcanzará el óptimo global (por ejemplo, el sendero A). Con\(V_{A,1,2}=0\) nuestro tamaño de paso por generación para cada rasgo siendo independientes entre sí.
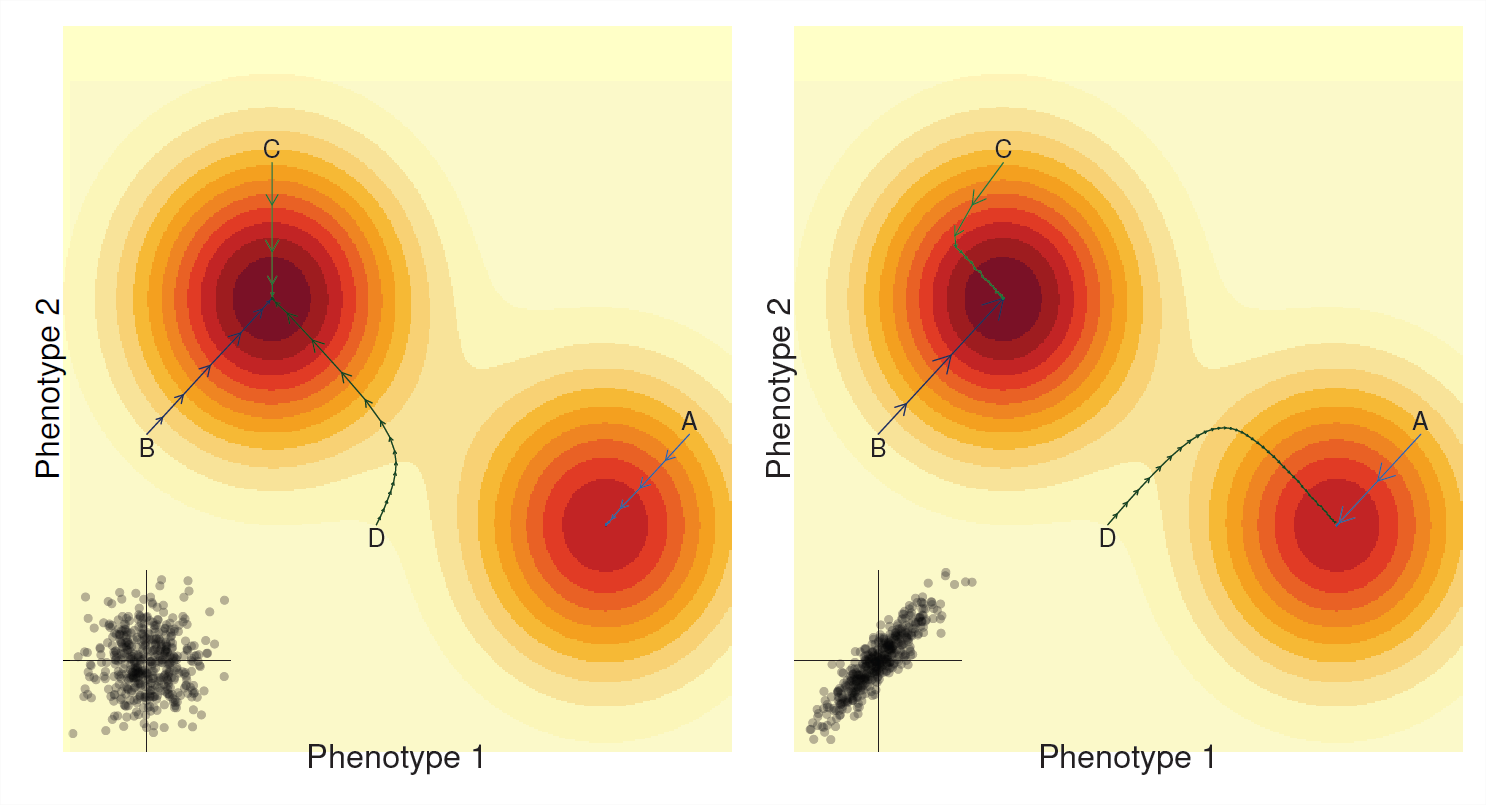
La historia puede ser bastante diferente si existe una fuerte correlación genética entre los dos fenotipos (Figura del lado derecho\(\PageIndex{6}\)), ahora el camino tomado por nuestra población está sesgado hacia ser fuerte a lo largo de los ejes de la correlación genética. A veces, la correlación genética puede ayudar a la progresión cuesta arriba cuando la correlación genética se alinea con la pendiente (por ejemplo, las rutas A y B) ya que la selección en un fenotipo aumenta la selección en el otro fenotipo. Sin embargo, las correlaciones genéticas pueden obligar a la población a tomar caminos extraños hacia picos de aptitud física y la marcha puede ser lenta cuando el camino hasta el pico se encuentra a lo largo de un eje perpendicular a la covarianza en nuestros rasgos (últimas partes del camino C & D) En algunos casos la población puede incluso evolucionar a una pico diferente debido a correlaciones genéticas (comparar la ruta D en paneles izquierdo y derecho).
De manera más general, podemos extender esto a un número arbitrario de fenotipo escrito en el paisaje de la aptitud Ecuación del criador, en notación matricial, como
\[{\bf R} = \frac{1}{\bar{w}} {\bf G} \nabla \bar{w} ({\bar{x}})\]
donde\(\nabla\) es el operador de gradiente vectorial, tomando la derivada por el vector de fenotipos medios, tal que\(\nabla \bar{w} = \left( \frac{\partial \bar{w}}{\partial \bar{x}_1},~ \frac{\partial \bar{w}}{\partial \bar{x}_2},~\cdots \right)\). Así, la respuesta evolutiva a corto plazo de la población a la selección es desplazar sus fenotipos medios (\(R\)) en un directo que localmente aumente la aptitud media de la población (\(\nabla_{\bar{x}} \bar{w}\)) pero esta escalada de forma física de nuestra población está moderada por las covarianzas genéticas entre nuestros rasgos (\({\bf G}\)).
Las ideas sobre paisajes adaptativos de fitness son clave para comprender el papel de la ecología en la especiación. Las especies pueden mantenerse distintas ante el mestizaje si los híbridos entre las especies están mal adaptados a cualquiera de los nichos de las especies parentales (una llamada barrera postcigótica extrínseca para una hibridación exitosa). Desde una perspectiva del paisaje de fitness esto corresponde a especies que ocupan diferentes picos de fitness, de tal manera que los híbridos entre las dos poblaciones, quienes serán intermedios en fenotipo, por lo que caen en el valle entre los picos, es decir, tienen baja aptitud.
Algunas aplicaciones de la ecuación del obtentor de rasgos multivariados
La ecuación de los criadores multivariados tiene muchos usos diferentes en la comprensión de la respuesta de múltiples rasgos a la selección. También ofrece fuertes conocimientos sobre los fundamentos mecanicistas de la selección de parientes y la selección sexual. Los discutiremos a continuación.
Selección sexual y evolución de la preferencia de pareja por beneficios indirectos.
Los organismos a menudo ponen un enorme esfuerzo en encontrar y atraer parejas, a veces a un costo considerable para sus posibilidades de supervivencia. ¿Por qué los individuos son tan selectivos sobre con quién se aparean, particularmente cuando su elección parece basarse en personajes elaborados y demostraciones arbitrarias que seguramente reducen la viabilidad de sus compañeros?

Una de las principales razones por las que los individuos evolucionan para ser exigentes sobre con quién se aparean es que puede afectar directamente su estado físico. Al elegir una pareja con características particulares, los individuos pueden obtener más cuidado parental para su descendencia, evitar parásitos, o estar eligiendo una pareja con mayor fertilidad. Por ejemplo, los gusanos luminosos hembra destellan por la noche para atraer a los machos que pasan volando. Las hembras con linternas más grandes y brillantes tienen mayor fecundidad, por lo que los machos con preferencia por destellos más brillantes obtendrán un beneficio directo para su propia condición física. (Obsérvese que los varones se beneficiarán aunque estas diferencias en la fecundidad femenina sean impulsadas enteramente por las diferencias en el entorno, y por lo tanto no heredables). De hecho, los gusanos resplandecientes machos han evolucionado para ser atraídos por señuelos parpadeantes

Sin embargo, incluso en ausencia de beneficios directos de elección, la selección puede favorecer indirectamente la evolución de la elección. Estos beneficios indirectos ocurren porque los individuos pueden tener una descendencia de mayor aptitud al elegir una pareja cuyo fenotipo indique una alta viabilidad (la llamada hipótesis de los 'buenos genes'), o eligiendo una pareja cuyo fenotipo sea simplemente atractivo, y probablemente produzca descendencia igualmente atractiva (la 'fugaz' o hipótesis de 'hijos sexy').

Denotaremos un rasgo de visualización, por ejemplo, longitud de la cola, en machos por\(\mars\) y un rasgo de preferencia en hembras por\(\venus\). Nuestro rasgo de exhibición está bajo selección directa en machos, de tal manera que su respuesta a la selección puede escribirse como
\[R_{\mars} = \beta_{\mars} V_{A, \mars}\]
Supongamos que el rasgo de preferencia femenina, el grado en que las hembras se sienten atraídas por las colas largas, no está bajo selección directa\(\beta_{\venus}=0\). Entonces la respuesta a la selección del rasgo de preferencia puede escribirse como
\[\begin{aligned} R_{\venus} &=\beta_{\venus}V_{A,\venus} + \beta_{\mars} V_{A, \venus \mars} & = \beta_{\mars} V_{A, \venus \mars}\end{aligned}\]
Por lo que la preferencia femenina responderá a la selección si está genéticamente correlacionada con el rasgo masculino, es decir, si no\(V_{A, \venus \mars}\) es cero. Hay una serie de diferentes formas en que esta correlación genética podría surgir; la más simple es que los loci subyacentes al rasgo masculino pueden tener un efecto pleiotrópico en la preferencia femenina. Sin embargo, la preferencia femenina a menudo puede tener una base genética bastante distinta de los rasgos de exhibición masculinos.
Una forma más general en la que pueden surgir correlaciones genéticas de preferencias de rasgos es a través del apareamiento selectivo. Como las hembras varían en su preferencia de longitud de cola, las que tienen preferencia por colas más largas se aparearán con machos de cola larga y lo contrario para las hembras con preferencia por colas más largas. Por lo tanto, se establecerá una correlación genética entre los rasgos de visualización y preferencia (ver Figura\ ref {fig:assort_mating_2_trait}).
Los machos con las colas más largas también portarán los alelos asociados con la preferencia por colas más largas, ya que sus papás de cola larga tendían a aparearse con hembras con preferencia genética por colas largas. De igual manera, los machos con colas más cortas portarán alelos asociados con la preferencia por colas más cortas. Así, si hay selección directa para machos con colas más largas, entonces la preferencia femenina por colas más largas también aumentará, ya que se correlaciona genéticamente a través del apareamiento selectivo.

Como ejemplo de cómo la selección directa en los rasgos de visualización puede impulsar la evolución de los rasgos de preferencia, consideremos algunos datos de guppies. Los Guppies (Poecilia reticulata) son un sistema clásico para estudiar la interacción de la selección natural y sexual. En algunas poblaciones de guppies, las hembras muestran preferencia por los machos con más coloración anaranjada.

estableció cuatro pares poblacionales replicados de guppies y seleccionó uno de cada par para una coloración anaranjada incrementada o disminuida en los machos, seleccionando la parte superior/inferior\(20\) de\(50\) los machos. Eligió aleatoriamente hembras de cada población para formar la siguiente generación, por lo que no ejerció selección directa sobre las hembras. Midió la respuesta a la selección en la coloración masculina y en la preferencia femenina por el naranja (paneles izquierdo y derecho de la Figura\ ref {fig:assort_mating_guppies} respectivamente). En las líneas que se seleccionaron para machos más anaranjados, las hembras mostraron una mayor preferencia por el naranja. Mientras que en aquellas líneas seleccionadas por menos naranja en las exhibiciones masculinas, las hembras mostraron una menor preferencia por el naranja. Esto es consistente con la selección indirecta en la preferencia naranja femenina como respuesta a la selección en la coloración masculina, debido a una correlación genética entre la preferencia femenina y el rasgo masculino. A priori es poco probable que la pleiotropía sea la fuente de la correlación genética entre estos rasgos, más bien es probable que sea causada por hembras que se aparean surtativamente con machos que coinciden con su preferencia de color.
Volviendo a nuestro ejemplo de cola de pájaro, ¿qué podría impulsar la selección directa en la longitud de la cola masculina? La selección de colas más largas en machos podría producirse porque las colas más largas están correlacionadas genéticas con una mayor viabilidad masculina, por ejemplo quizás solo los machos que recolectan un exceso de alimento tienen los recursos para invertir en el cultivo de cola larga, es decir, una cola larga es una señal honesta de aptitud física. Esto correspondería a una explicación de 'buenos genes' de la evolución de la elección de pareja femenina.
Hay otra manera más sutil de que la selección podría favorecer nuestro rasgo masculino. Imagínese que la variación en el rasgo de preferencia femenina se debe a que algunas hembras no tienen una fuerte preferencia por la longitud de la cola masculina, pero algunas hembras tienen una fuerte preferencia por los machos con colas más largas.

Los machos con colas más largas tendrían entonces mayor fecundidad que los machos de cola corta ya que hay un subconjunto de hembras que se sienten fuertemente atraídas por las colas largas, y estos machos también llegan a aparearse con las otras hembras. Así, la selección favorece a los machos de cola larga, y así indirectamente favorece la preferencia femenina por colas más largas; las hembras con preferencia por colas más largas tienen hijos que a su vez son más atractivos. A este modelo se le llama a veces el modelo sexy-son. También se le llama el modelo fugitivo fisheriano, ya que la preferencia femenina y el rasgo masculino pueden coevolucionar de una manera creciente impulsando preferencias cada vez más extremas por rasgos arbitrarios. Así, muchos rasgos extravagantes de exhibición en machos y hembras pueden existir puramente porque los individuos los encuentran hermosos y se sienten atraídos por ellos.
La regla de Hamilton y la evolución de comportamientos altruistas y egoístas
“'La única razón para hacer un zumbido que conozco es porque eres una abeja. ' Entonces [Pooh] pensó otro largo tiempo, y dijo: 'La única razón para ser una abeja que conozco es para hacer miel... Y la única razón para hacer miel es para que pueda comerla. '” —Winnie-the-Pooh,.
Uno de los cambios sísmicos causados por el trabajo de Darwin fue la constatación de que los organismos no existen en beneficio de otros individuos u otras especies. Las abejas no evolucionaron para polinizar las flores, más de lo que evolucionaron para hacer miel para osos. Si podemos decir que hay una 'razón' por la que existe un organismo es sólo para dejar descendencia a la siguiente generación. Pooh puede ser perdonado por desviarse del pensamiento darwiniano, ya que existe en beneficio de Christopher Robin y otros cuentos infantiles antes de acostarse.
Sin embargo, hay una arruga en esta visión darwiniana. Las abejas obreras no hacen miel para beneficiar a sus crías, son estériles y están trabajando en beneficio de la abeja reina y su descendencia. Los individuos frecuentemente se comportan de manera que sacrifican su propia aptitud en beneficio de los demás. Esa selección favorece tales actos aparentes de altruismo es desconcertante a primera vista. Suministró la primera explicación evolutiva general de tal altruismo. Su intuición fue que mientras un individuo está perdiendo algún rendimiento reproductivo, los alelos subyacentes a un comportamiento altruista aún pueden propagarse en la población si este costo es superado por los beneficios obtenidos a través de la transmisión de estos alelos a través de un individuo relacionado. Obsérvese que esto significa que el alelo no está actuando de manera abnegada, a pesar de que los individuos pueden como resultado.
El altruismo refleja las interacciones sociales. Entonces, como modelo simple, imaginemos que los individuos interactúan en parejas,\(i\) siendo nuestro individuo focal emparejado con un individuo\(j\). Imagínese que los individuos tienen dos fenotipos posibles\(X=1\) o\(0\), correspondientes a proporcionar o retener algún pequeño acto de 'altruismo' (con la misma facilidad podríamos voltear estas etiquetas y llamarlas acto desinteresado y acto egoísta respectivamente). Nuestras parejas de individuos que interactúan podrían, por ejemplo, ser hermanos compartiendo un nido. El rasgo altruista podría ser tan sencillo como crecer a un ritmo ligeramente más lento para reducir la competencia de hermanos por la comida de los padres, o actos más complicados de altruismo como los hijos que renuncian a su propia reproducción para ayudar a sus padres a criar a sus hermanos.
Proporcionar el acto altruista tiene un costo\(C\) para la idoneidad de nuestro individuo y no proporcionar este acto no tiene costo alguno. Recibir este acto altruista confiere un beneficio de idoneidad\(B\) sobre los individuos que no recibieron este acto. La regla establece que tal rasgo se extenderá por la población si
\[2F B > C\]
donde\(F\) es el coeficiente de parentesco promedio entre los individuos que interactúan (\(i\)y\(j\)). En la formulación habitual de la Regla de Hamilton nuestro\(2F\) se sustituye por el 'Coeficiente de relación', que es la proporción de alelos compartidos entre los individuos. Aquí usamos dos veces el coeficiente de parentesco para mantener las cosas alineadas con nuestra notación para estos capítulos. Tenga en cuenta que si nuestros individuos son ellos mismos endogámicos necesitamos hacer un poco más de cuidado para conciliar estas dos medidas. Por lo que el comportamiento altruista se extenderá aunque sea costoso para el individuo si su costo es pagado por el beneficio a individuos suficientemente relacionados.
Como ejemplo de selección de parientes, considere el trabajo sobre el cortejo cooperativo en pavos salvajes (Meleagris gallopavo). Los pavos machos a menudo forman asociaciones de exhibición, con un macho subordinado que ayuda a un macho dominante a mostrarse a las hembras y defender a las hembras de otros grupos de machos.

Estas parejas suelen ser hermanos completos (\(F=0.25\)), siendo el macho subordinado a menudo el más joven de los dos. El macho subordinado a menudo pierde oportunidades de apareamiento a lo largo de toda su vida al actuar como wingman para sus hermanos mayores. Estimó que los machos dominantes ganaron una\(6.1\) descendencia extra cuando se muestran con una pareja que los machos que se muestran solos. Los machos subordinados pierden al engendrar\(0.9\) descendencia en comparación con los machos solitarios. Así, los costos de ayudar por los varones subordinados son más que compensados por las ganancias de aptitud de sus hermanos (\((2 \times 0.25) \times 6.1 > 0.9\)), por lo que la evolución de esta ayuda altruista en el cortejo cooperativo es potencialmente bien explicada por la selección de parentesco.
¿Cómo se cambiaría esta respuesta si las asociaciones masculinas de Turquía fueran solo\(\frac{1}{2}\) hermanos, o primos hermanos?
[Fig:Hamilton_B_C]
¿De dónde viene este resultado? Bueno, podemos usar nuestro marco genético cuantitativo para obtener cierta intuición derivando una versión simple de la Regla de Hamilton al pensar en los fenotipos de los parientes de un individuo como fenotipos genéticamente correlacionados. Para esbozar una prueba de este resultado, supongamos que la aptitud de nuestro\(i\) individuo focal se puede escribir como
\[W(i,j)= W_0 + W_i +W_j\]
donde\(W_i\) es la contribución de la aptitud del individuo\(i\) debido a su propio fenotipo, y\(W_j\) es la contribución a la aptitud de nuestro individuo debido al comportamiento\(i\)\(j\) del individuo que interactúa (i.e. \(j\)ej., fenotipo). Con el beneficio\(B\) y costo\(C\), nuestros\(W(i,j)\) se representan en la Figura\ ref {fig:hamilton_b_c}.
Siguiendo la ecuación de nuestro obtentor multivariado, podemos escribir el cambio esperado de nuestro fenotipo conductual como
\[R = \beta_i V_A + \beta_j V_{A,i,j},\]
Nuestro fenotipo altruista está aumentando en la población si\(R>0\), i.e.
\[\beta_i V_A + \beta_j V_{A,i,j} > 0\]
La pendiente\(\beta_i\) de la regresión del fenotipo conductual de nuestro individuo focal sobre la aptitud es proporcional a\(-C\). La pendiente\(\beta_j\) de la regresión del fenotipo de nuestro compañero que interactúa sobre la aptitud de nuestro individuo focal es proporcional a\(B\) (con la misma constante de proporcionalidad). Por lo tanto, nuestro fenotipo altruista está aumentando en la población si
\[\begin{aligned} \beta_i V_A + \beta_j V_{A,i,j} & > 0 \nonumber \\ B \frac{V_{A,i,j}}{V_A} & > C \label{eqn:Covar_Hamilton}\end{aligned}\]
Entonces, ¿cuál es la covarianza genética promedio entre el individuo\(i\) y\(j\) el fenotipo altruista? Es el mismo fenotipo conductual en ambos individuos, por lo que los fenotipos están genéticamente correlacionados si nuestros individuos están relacionados entre sí. La covarianza del mismo fenotipo entre dos individuos es justa\(2 F_{i,j} V_A\) (ver\ ref {additive_covar_general_rellys}). Entonces nuestro fenotipo altruista va en aumento en la población si
\[\begin{aligned} B\frac{2 F_{i,j} V_A}{V_A} &> C \nonumber \\ 2 F_{i,j} B & > C \label{eqn:Hamiltons_rule}\end{aligned}\]
Visto desde esta perspectiva, la regla es simplemente una afirmación de que los comportamientos altruistas pueden propagarse a través de la selección de parentesco, si el costo promedio para un individuo de mostrar un fenotipo altruista, es decir, portar alelos altruistas, se paga a través del beneficio promedio de interactuar con parientes altruistas (parientes).

Bajo la selección de parentesco, la relación y la estructura reproductora de las poblaciones se hipotetizan como un factor clave para determinar la evolución de los comportamientos altruistas. Un ejemplo más impresionante de la evolución del altruismo es la evolución repetida de la eusocialidad, donde las castas estériles han evolucionado para ayudar a criar a sus hermanos más que a su propia descendencia. La eusocialidad ha evolucionado al menos ocho veces independientes en Hymenoptera (abejas, avispas y hormigas). Hay una gran variación en los sistemas de apareamiento en himenópteros desde altos niveles de apareamiento múltiple hasta monandry. realizó un análisis filogenético comparativo del sistema de apareamiento en cientos de especies de himenópteros. Encontraron que cada uno de los ocho clados eusociales tenía monandria, las hembras se apareaban con un solo macho, como estado ancestral. Así, la eusocialidad evolucionó inicialmente en poblaciones donde se maximizó la relación entre hermanos.

Otras formas de altruismo
La selección de Kin puede favorecer el altruismo porque los individuos portadores de alelos altruistas interactúan con otros individuos relacionados que tienden a mostrar fenotipos altruistas y así obtener una ventaja. Sin embargo, hay otras formas en que los comportamientos altruistas pueden propagarse que solo a través de las interacciones con los parientes.
Existe un problema inherente con la cooperación entre los no familiares. Los tramposos suelen ganar. Para ver el dilema de la cooperación consideremos el dilema clásico del preso. Imagínese que dos delincuentes son capturados por la policía, no hay pruebas suficientes para obtenerlos del cargo principal pero serán condenados por un cargo menor. Los presos no se conocen bien, nunca antes habían trabajado juntos. Enfrentan un año de prisión cada uno por el menor cargo. La policía ofrece a cada preso un trato, testifica en contra de su coacusado y retiraremos todos los cargos en su contra, su coacusado tendrá tres años. Si ambos optan por agotarse, cada uno obtendrá dos años. El resultado mejor combinado para los acusados es colaborar entre sí y guardar silencio, cada uno cumplirá un año. No obstante, los acusados no pueden conferir, y cada uno no tiene forma de saber si el otro lo ha chillado y delatado. La elección racional en esta interacción única es vender a tus compañeros prisioneros. Hay muchas situaciones como esta donde una interacción entre individuos tiene el mejor resultado si trabajan juntos. Sin embargo, como los individuos podrían engañar a la interacción, el resultado racional puede ser no cooperar. Para situarlo en un entorno evolutivo, podríamos imaginar que la aptitud de los organismos en una población dependía de sus estrategias en el juego de dilemas de un prisionero único, por ejemplo, emparejar individuos al azar. En tales entornos, un individuo infiel tendría mayor aptitud física que un altruista, y así la población evolucionaría a todos tramposos. Sin embargo, la cooperación entre no familiares ha evolucionado muchas veces.
| Silencioso (Coopera) | Confiesa (Trucos) | |
|---|---|---|
| Silencioso (Coopera) | 1, 1 | 3, 0 |
| Confiesa (Trucos) | 0, 3 | 2, 2 |
El factor clave que condujo a un comportamiento no cooperativo en el dilema de este preso fue la naturaleza puntual de la interacción. La estrategia óptima cambia cuando nuestros socios enfrentan esta situación juntos varias veces, por ejemplo, si nuestros pandilleros son arrastrados regularmente a lo largo de los años en sus vidas en el crimen. Intuitivamente, si uno de nuestros presos sabe que su compañero pandillero no la traicionó la última vez entonces podrías esperar que estaría más inclinada a confiar en ellos y no traicionarlos esta vez. Esta configuración se llama el dilema iterativo del prisionero, con nuestros prisioneros enfrentando el 'juego' con los costos y beneficios repetidamente con conocimiento de cómo se comportó el otro jugador en rondas anteriores del juego. En este escenario iterado, es posible una estrategia simple de 'ojo por ojo'. Los jugadores que siguen esta estrategia inician el juego cooperando, y luego copian la estrategia del otro preso del último movimiento (si el otro preso cooperó la última vez que cooperan esta vez, y de manera similar para hacer trampa). Imagínese nuevamente nuestra población de organismos que ahora están emparejados aleatoriamente para jugar juegos iterados por su estado físico. Si muchos individuos en la población juegan una estrategia ojo por ojo, un individuo infiel en esta población tiene menor condición física que un individuo ojo por ojo. Los individuos que juegan una estrategia ojo por ojo no cooperan con los tramposos, por lo que pagan poco costo relativo por interactuar con estos individuos, pero obtienen los beneficios de la cooperación con otros individuos altruistas. Así, puede evolucionar el 'altruismo recíproco', donde los individuos brindan una ayuda costosa a las personas que esperan que correspondan en alguna fecha futura. Tenga en cuenta que no hay nada verdaderamente altruista en el altruismo recíproco, los individuos que interactúan simplemente están actuando para aumentar su forma directa a lo largo de sus vidas y, como tal, la interacción es mutuamente beneficiosa. Así, algunos prefieren el nombre 'reciprocidad' en lugar de 'altruismo recíproco'.
Podemos usar nuestro marco de reglas de Hamilton para comprender la evolución del altruismo recíproco con más detalle. Los únicos requisitos para que la regla de Hamilton prediga la propagación de un comportamiento altruista es que
\[\begin{aligned} B \frac{Cov(X_i,X_j)}{V_A} & > C \end{aligned}\]
esto es lo mismo que la Ecuación\ ref {EQN:Covar_Hamilton} donde ahora hemos escrito\(V_{A,i,j}\) como una covarianza entre el fenotipo conductual de nuestro individuo focal\(i\) y los individuos que interactúan\(j\).

Entonces necesitamos un nivel suficientemente positivo de covarianza entre el comportamiento altruista del individuo\(i\) y el de los individuos que interactúan para superar los costos, es decir, los altruistas interactúan suficientemente a menudo con los altruistas para permitir que los individuos altruistas que están pagando costos en promedio recibir los beneficios de acondicionamiento físico de otras personas. Bajo modelos de selección de kin-selección, esta covarianza positiva proviene de la covarianza genética positiva que interactúa con miembros de la familia. Sin embargo, esta covarianza positiva también puede surgir si los altruistas muestran estrategias dependientes del contexto, como ojo por ojo, donde solo son altruistas hacia individuos que no los han engañado recientemente en el pasado. Tenga en cuenta que realmente estamos estirando nuestro uso de la ecuación del obtentor multivariado aquí, estas covarianzas ahora no son realmente covarianzas genéticas. Estas covarianzas no son entre rasgos en un mismo individuo, o entre individuos relacionados, son covarianzas de rasgos por individuos que interactúan con individuos cooperativos similares. Estos individuos que interactúan ni siquiera tienen que ser las mismas especies aquí, ya que estos modelos pueden ser utilizados para comprender la evolución de los mutualismos entre especies.
Encontramos altruismo en algunos lugares aparentemente extraños. Los murciélagos vampiros (Desmodontinae), como su nombre indica, se alimentan únicamente de la sangre de otros animales. No obstante, la sangre no es del todo el superalimento que Drácula te haría creer. La sangre es principalmente agua. Volar es increíblemente enérgico, por lo que los murciélagos tienen que consumir la mitad de su peso corporal en sangre una noche y morirán rápidamente si van sin comer. A menudo es difícil encontrar suficiente sangre en una noche, por lo que quienes se pierden la alimentación solo sobreviven de otros murciélagos que comparten sus harinas de sangre. Los murciélagos vampiro comparten sus comidas con sus familiares, pero también con individuos no relacionados. Como lo predice el altruismo recíproco, tienden a compartir con individuos que previamente han compartido alimentos con ellos, por lo que el intercambio de alimentos puede verse como un comportamiento adaptativo.
La selección natural rara vez actúa sobre un rasgo de forma aislada, más bien la selección a menudo actúa sobre muchos rasgos a la vez. Así, la respuesta a corto plazo de la selección sobre un rasgo también refleja la selección en otros rasgos parcialmente correlacionados genéticamente. Muchas compensaciones evolutivas, entre diferentes aspectos de la aptitud física, se pueden pensar en estos términos.
La respuesta entre generación de múltiples rasgos a la selección puede ser entendida y predicha por la ecuación del obtentor multi-variable (múltiples rasgos). La respuesta de un rasgo (\(R_1\)) depende de la varianza genética aditiva para ese rasgo y del gradiente de selección directa sobre el rasgo (\(V_{A,1} \beta_1\)), esta respuesta directa se modifica por selección indirecta sobre el rasgo o rasgos (\(2\)) que genéticamente covaran ( \(V_{A,12} \beta_2\)).
Podemos estimar los gradientes de selección lineal y direccional mediante la regresión lineal multivariada de aptitud en fenotipos.\(\beta\) Podemos incorporar la selección estabilizadora, disimulativa y covariante entre rasgos al incluir términos cuadráticos para los fenotipos en esta regresión.
Podemos interpretar la ecuación multivariante del obtentor en términos de un enfoque de paisaje de fitness, y ver que la selección natural puede conducir a nuestra población hacia picos locales de aptitud media. Sin embargo, el camino que toma está sesgado para alinearse mejor con las correlaciones genéticas entre rasgos, lo que en algunos casos puede ralentizar la respuesta de nuestra población a la selección.
La ecuación multivariante del obtentor se aplica en muchos lugares de la teoría evolutiva. Por ejemplo, la evolución de la selección indirecta para la preferencia de pareja es una aplicación, ya que la correlación genética establecida por el apareamiento selectivo entre los rasgos de preferencia y los rasgos de visualización es clave para entender por qué la preferencia de pareja puede responder a la selección indirecta. También vimos cómo se pueden desarrollar modelos de selección de parentesco para entender el altruismo y la regla de Hamilton usando la ecuación del obtentor multivariado al ver a los familiares como que tienen aptitudes genéticamente covariables.
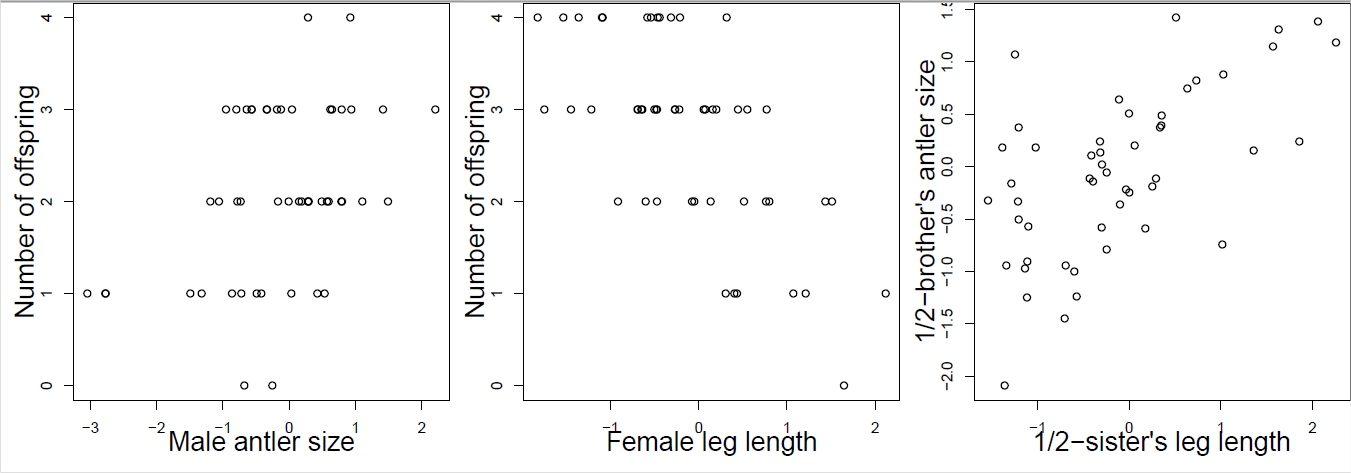
Usted recolecta observaciones de ciervos rojos dentro de una generación, registrando el número de crías y fenotipos de un individuo para una serie de rasgos que se sabe que tienen variación genética aditiva. Usando tus datos, construyes las gráficas que se muestran en la Figura\ ref {fig:Red_Deer_Q} (estandarizando los fenotipos). Responda las siguientes preguntas eligiendo una de las opciones en negrita. Justifica brevemente cada una de tus respuestas con referencia a la ecuación del obtentor y a la ecuación del obtentor de múltiples rasgos.
- Mirando solo a la figura\ ref {fig:Red_Deer_Q} A, ¿en qué dirección esperas que evolucione el tamaño de asta masculina? Información insuficiente, incremento, disminución.
- Mirando solo las figuras\ ref {fig:Red_Deer_Q} B y C, ¿en qué dirección esperas que evolucione el tamaño de asta masculina? Información insuficiente, incremento, disminución.
- Mirando las figuras\ ref {fig:red_deer_q} A, B y C, ¿en qué dirección esperas que evolucione el tamaño de asta masculina? Información insuficiente, incremento, disminución.