B: Conceptos básicos matemáticos
- Page ID
- 54834
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Plazas y Otros Poderes
Un exponente, o una potencia, es una taquigrafía matemática para multiplicaciones repetidas. Por ejemplo, el exponente “2” significa multiplicar la base para ese exponente por sí mismo (en el ejemplo aquí, la base es “5”):
\[5^2=5×5=25\]
El exponente es “2” y la base es el número “5”. Esta expresión (multiplicar un número por sí misma) también se llama cuadrado. Cualquier número elevado a la potencia de 2 está siendo cuadrado. Cualquier número elevado a la potencia de 3 está siendo cúbico:
\[5^3=5×5×5=125\]
Un número elevado a la cuarta potencia es igual a ese número multiplicado por sí mismo cuatro veces, y así sucesivamente para potencias superiores. En general:
\[n^x=n×n^{x−1}\]
Cálculo de porcentajes
Un porcentaje es una forma de expresar una cantidad fraccionaria de algo usando un todo dividido en 100 partes. Un por ciento es una relación cuyo denominador es 100. Utilizamos el símbolo de porcentaje,%, para mostrar el porcentaje. Así, 25% significa una relación de\(\frac{25}{100}\), 3% significa una relación de\(\frac{3}{100}\), y 100% por ciento significa\(\frac{100}{100}\), o un todo.
Conversión de porcentajes
Un porcentaje se puede convertir en una fracción escribiendo el valor del porcentaje como una fracción con un denominador de 100 y simplificando la fracción si es posible.
\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]
Un porcentaje se puede convertir a decimal escribiendo el valor del porcentaje como una fracción con un denominador de 100 y dividiendo el numerador por el denominador.
\[10\%=\dfrac{10}{100}=0.10\]
Para convertir un decimal a un porcentaje, escriba el decimal como fracción. Si el denominador de la fracción no es 100, conviértala a una fracción con un denominador de 100, y luego escribe la fracción como un porcentaje.
\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]
Para convertir una fracción en un porcentaje, primero convierta la fracción a un decimal, y luego convierta el decimal a un porcentaje.
\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]
Supongamos que un investigador encuentra que 15 de los 23 estudiantes de una clase son portadores de meningitides de Neisseria. ¿Qué porcentaje de estudiantes son portadores? Para encontrar este valor, primero exprese los números como una fracción.
\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]
Luego divide el numerador por el denominador.
\[\dfrac{15}{23}=15\div 23 \approx 0.65\]
Por último, para convertir un decimal a un porcentaje, multiplicar por 100.
\[0.65 \times 100=65\%\]
El porcentaje de estudiantes que son portadores es de 65%.
También podrías obtener datos sobre ocurrencia y no ocurrencia; por ejemplo, en una muestra de estudiantes, 9 dieron positivo para anticuerpos contra Toxoplasma, mientras que 28 dieron negativo. ¿Cuál es el porcentaje de estudiantes seropositivos? El primer paso es determinar el “todo”, del que forman parte los alumnos positivos. Para ello, suma las pruebas positivas y negativas.
\[\mathrm{positive+negative=9+28=37}\]
Toda la muestra estuvo conformada por 37 estudiantes. La fracción de positivos es:
\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]
Para encontrar el porcentaje de estudiantes que son portadores, dividir el numerador por el denominador y multiplicar por 100.
\ [\ dfrac {9} {37} =9\ div 37\ aprox 0.24\
0.24\ veces 100=24\%\]
El porcentaje de estudiantes positivos es de aproximadamente 24%.
Otra forma de pensar en calcular un porcentaje es establecer fracciones equivalentes, una de las cuales es una fracción con 100 como denominador, y multiplicar de manera cruzada. El ejemplo anterior se expresaría como:
\[\dfrac{9}{37}=\dfrac{x}{100}\]
Ahora, cruzar multiplicar y resolver por lo desconocido:
\ [\ begin {align}
9\ times 100 &=37 x & &\ nonumber\\ [5pt]
\ frac {9\ times 100} {37} &=x & &\ text {Divide ambos lados por 37}\ nonumber\\ [5pt]
\ frac {900} {37} &=x & &\ text {Multiplicar}\ nonumber\\ [5pt]
24 &\ x x aprox &\ text {Dividir}\ nonumber
\ end {align}\]
La respuesta, redondeada, es la misma.
Multiplicar y dividir por decenas
En muchos campos, especialmente en las ciencias, es común multiplicar decimales por potencias de 10. Veamos qué pasa cuando multiplicamos 1.9436 por algunos poderes de 10.
\ [\ begin {align}
1.9436 (10) &=19.436\ nonumber\\
1.9436 (100) &=194.36\ nonumber\\
1.9436 (1000) &=1943.6\ nonumber
\ end {align}\]
El número de lugares que mueve el punto decimal es el mismo que el número de ceros en la potencia de diez. La tabla\(\PageIndex{1}\) resume los resultados.
| Multiplicar por | Ceros | Se mueve el punto decimal. |
|---|---|---|
| 10 | 1 | 1 lugar a la derecha |
| 100 | 2 | 2 lugares a la derecha |
| 1,000 | 3 | 3 lugares a la derecha |
| 10,000 | 4 | 4 lugares a la derecha |
Podemos usar este patrón como atajo para multiplicar por potencias de diez en lugar de multiplicar usando el formato vertical. Podemos contar los ceros en la potencia de 10 y luego mover el punto decimal ese mismo número de lugares hacia la derecha.
Entonces, por ejemplo, para multiplicar 45.86 por 100, mueva el punto decimal 2 lugares a la derecha.
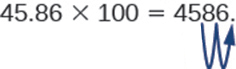
A veces cuando necesitamos mover el punto decimal, no hay suficientes cifras decimales. En ese caso, usamos ceros como marcadores de posición. Por ejemplo, multipliquemos 2.4 por 100. Tenemos que mover el punto decimal 2 lugares a la derecha. Dado que solo hay un dígito a la derecha del punto decimal, debemos escribir un 0 en el lugar de las centésimas.
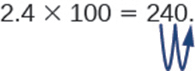
Al dividir por potencias de 10, simplemente tomar el enfoque opuesto y mover el decimal a la izquierda por el número de ceros en la potencia de diez.
Veamos qué pasa cuando dividimos 1.9436 por algunos poderes de 10.
\ [\ begin {align}
1.9436\ div 10&=0.19436\ nonumber\\
1.9436\ div 100&=0.019436\ nonumber\\
1.9436\ div 1000&=0.0019436\ nonumber
\ end {align}\]
Si no hay dígitos suficientes para mover el decimal, agregue ceros para crear lugares.
Notación Científica
La notación científica se utiliza para expresar números muy grandes y muy pequeños como producto de dos números. El primer número del producto, el término dígito, suele ser un número no menor que 1 y no mayor que 10. El segundo número del producto, el término exponencial, se escribe como 10 con un exponente. Algunos ejemplos de notación científica se dan en la Tabla\(\PageIndex{2}\).
| Notación estándar | Notación Científica |
|---|---|
| 1000 | 1 × 10 3 |
| 100 | 1 × 10 2 |
| 10 | 1 × 10 1 |
| 1 | 1 × 10 0 |
| 0.1 | 1 × 10 −1 |
| 0.01 | 1 × 10 −2 |
La notación científica es particularmente útil para números muy grandes y muy pequeños, como 1,230.000.000 = 1.23 × 10 9, y 0.00000000036 = 3.6 × 10 −10.
Expresar números en notación científica
Convertir cualquier número a notación científica es sencillo. Contar el número de lugares necesarios para mover el decimal junto al dígito distinto de cero más a la izquierda: es decir, para hacer el número entre 1 y 10. Después multiplica ese número por 10 elevado al número de lugares que moviste el decimal. El exponente es positivo si moviste el decimal a la izquierda y negativo si moviste el decimal a la derecha. Entonces
\[2386=2.386\times1000=2.386\times10^3\]
y
\[0.123=1.23\times0.1=1.23\times10^{-1}\]
La potencia (exponente) de 10 es igual al número de lugares en los que se desplaza el decimal.
Logaritmos
El logaritmo común (log) de un número es la potencia a la que se debe elevar 10 para igualar ese número. Por ejemplo, el logaritmo común de 100 es 2, porque 10 debe elevarse a la segunda potencia para igualar 100. Ejemplos adicionales están en la Tabla\(\PageIndex{3}\).
| Número | Forma Exponencial | Logaritmo Común |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 −1 | −1 |
| 0.001 | 10 −3 | −3 |
Para encontrar el logaritmo común de la mayoría de los números, necesitará usar el botón LOG en una calculadora.
Redondeo y Dígitos Significativos
Al informar los datos numéricos obtenidos a través de mediciones, utilizamos solo tantas cifras significativas como la precisión de la medición lo justifique. Por ejemplo, supongamos que un microbiólogo que utiliza un contador celular automatizado determina que hay 525.341 células bacterianas en una muestra de un litro de agua de río. No obstante, registra la concentración como 525,000 células por litro y utiliza este número redondeado para estimar el número de celdas que probablemente se encontrarían en 10 litros de agua de río. En esta instancia, los tres últimos dígitos de la cantidad medida no se consideran significativos. Se redondean para tener en cuenta las variaciones en el número de células que probablemente se producirían si se midieran más muestras.
La importancia de las cifras significativas radica en su aplicación a la computación fundamental. Además y resta, la suma o diferencia debe contener tantos dígitos a la derecha del decimal como aquellos en el menos cierto (indicado subrayando en el siguiente ejemplo) de los números utilizados en el cálculo.
Supongamos que un microbiólogo desea calcular la masa total de dos muestras de agar.
\ [\ begin {array} {l}
4.38\ subrayado {3}\ texto {g}\
\ subrayado {3.002\ subrayado {1}}\ texto {g}\\
7.38\ subrayado {5}\ texto {g}
\ end {array}\]
El menor seguro de las dos masas tiene tres decimales, por lo que la suma debe tener tres decimales.
En multiplicación y división, el producto o cociente no debe contener más dígitos que en el factor que contiene el menor número de cifras significativas. Supongamos que al microbiólogo le gustaría calcular la cantidad de reactivo que estaría presente en 6.6 mL si la concentración es de 0.638 g/mL.
\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]
Nuevamente, la respuesta solo tiene un decimal porque esta es la precisión del número menos exacto en el cálculo.
Al redondear números, aumente el dígito retenido en 1 si va seguido de un número mayor que 5 (“redondear”). No cambie el dígito retenido si los dígitos que siguen son menores a 5 (“redondear hacia abajo”). Si el dígito retenido es seguido por 5, redondea hacia arriba si el dígito retenido es impar, o redondear hacia abajo si es par (después del redondeo, el dígito retenido siempre será par).
Tiempo de Generación
Es posible escribir una ecuación para calcular los números de celda en cualquier momento si se conoce el número de celdas iniciales y el tiempo de duplicación, siempre y cuando las celdas se dividan a una velocidad constante. Definimos N 0 como el número inicial de bacterias, el número en el tiempo t = 0. N i es el número de bacterias en el tiempo t = i, un tiempo arbitrario en el futuro. Finalmente estableceremos j igual al número de generaciones, o el número de veces que la población celular se duplica durante el intervalo de tiempo. Entonces tenemos,
\[N_i=N_0\times2^j\]
Esta ecuación es una expresión de crecimiento por fisión binaria.
En nuestro ejemplo, N 0 = 4, el número de generaciones, j, es igual a 3 después de 90 minutos porque el tiempo de generación es de 30 minutos. El número de celdas se puede estimar a partir de la siguiente ecuación:
\ [\ begin {align}
n_i&=n_0\ tiempos2^j\ nonumber\\
N_ {90} &=4\ tiempos2^3\ nonumber\\
N_ {90} &=4\ tiempos8=32\ nonumber
\ end {align}\]
El número de células después de 90 minutos es de 32.
Número más probable
La tabla en Figura\(\PageIndex{1}\) contiene valores utilizados para calcular el ejemplo de número más probable dado en Cómo crecen los microbios.