1.4: Revisión de Laser Essentials

Cavidades lineales y de anillo:

Figura 1.9: Posibles configuraciones de cavidad. (a) Esquema de un láser de cavidad lineal. b) Esquema de un láser anular. [1]

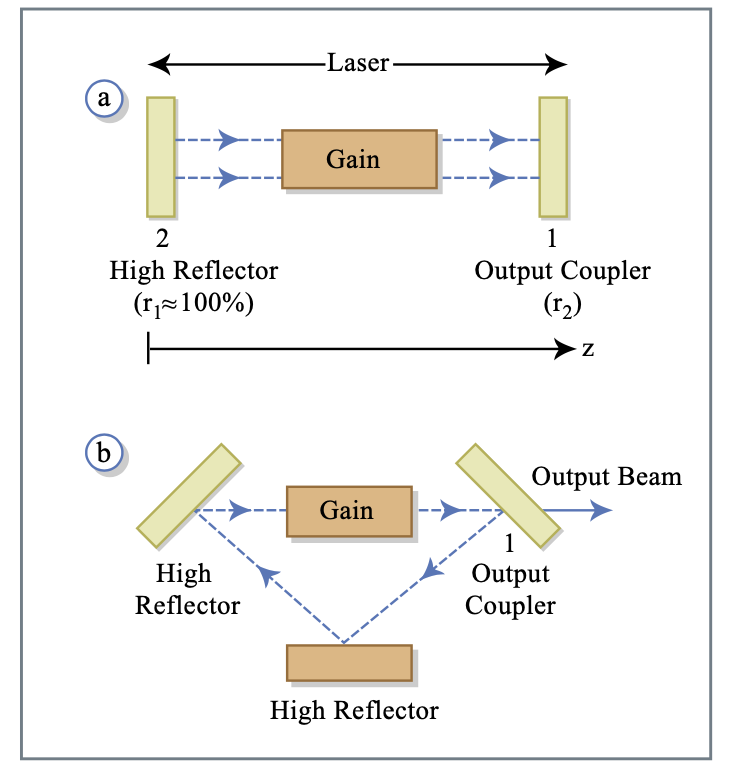
Operación en estado estacionario: El campo eléctrico debe repetirse después de un viaje de ida y vuelta. Considerar un campo monocromático polarizado linealmente

\[E(z, t) = \Re\{ E_0 e^{j(\omega t - kz)}\}, \nonumber \]

donde

\[k = \dfrac{\omega}{c} n \nonumber \]

es la constante de propagación en un medio con índice de refracción\(n\).

Considere el resonador lineal en la Figura 1.9a. La propagación de (1) a (2) está determinada por\(n = n' + jn''\) (índice de refracción complejo), con el campo eléctrico dado por

\[E = \Re \{ E_0 e^{\tfrac{\omega}{c} n_g'' \ell_g} e^{j\omega t} e^{-j \tfrac{\omega}{c}(n_g' \ell_g + \ell_a)} \}, \nonumber \]

donde\(n_g\) está el índice de refracción complejo del medio de ganancia (fuera del medio de ganancia\(n = 1\) se supone),\(\ell_g\) es la longitud del medio de ganancia,\(\ell_a\) es el medio de ganancia exterior, y\(\ell = n_g \ell_g + \ell_a\) es la longitud de la trayectoria óptica en el resonador.

La propagación de regreso a (1), es decir, una ida y vuelta completa da como resultado

\[E = \Re \{ r_1 r_2 e^{2\tfrac{\omega}{c} n_g'' \ell_g} E_0 e^{j\omega t -j 2 \tfrac{\omega}{c} \ell} \} \Rightarrow r_1 r_2 e^{2 \tfrac{\omega}{c} n_g'' \ell_g} = 1, \nonumber \]

es decir, la ganancia es igual a la pérdida, y además, obtenemos la condición de fase

\[\dfrac{2\omega \ell}{c} = 2m\pi. \nonumber \]

La condición de fase determina las frecuencias de resonancia, i.e.

\[\omega_m = \dfrac{m\pi c}{\ell} \nonumber \]

y

\[f_m = \dfrac{mc}{2\ell}. \nonumber \]

El espaciado de modo de los modos longitudinales es

\[\Delta f = f_m - f_{m - 1} = \dfrac{c}{2\ell} \nonumber \]

(solo cierto si no hay dispersión, es decir\(n \ne n(\omega)\)). Supongamos pérdida de cavidad independiente de frecuencia y ganancia en forma de campana (ver Figura 1.10).

Figura 1.10: Espectros de ganancia y pérdida de cavidad del láser, ubicación de modo longitudinal y salida láser para operación láser multimodo.

Figura 1.11: Espectros de ganancia y pérdida, ubicaciones de modo longitudinal y salida láser para operación láser monomodo.

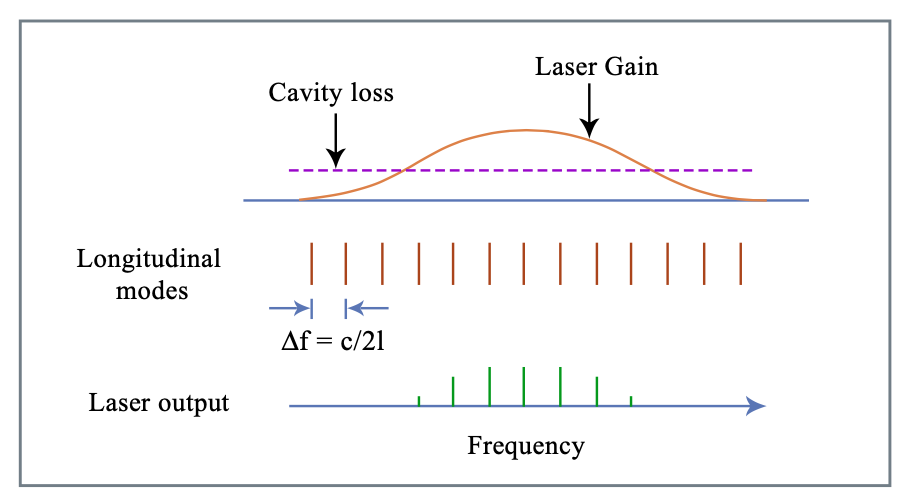
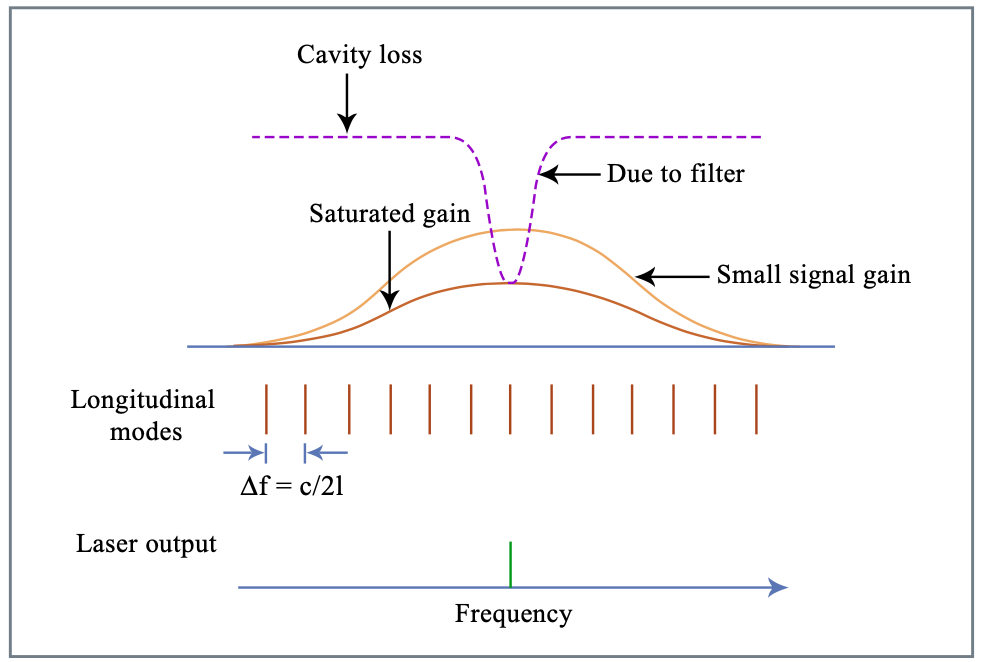
Para asegurar la operación de frecuencia única, use el filtro (etalon); distinga los medios de ganancia homogéneamente y no homogéneamente ensanchados, ¡los efectos de la quema de agujeros espectrales! Distinguir entre ganancia de señal pequeña g0 por ida y vuelta, es decir, ganancia para la intensidad del láser\(I \to 0\), y ganancia de señal grande, dada más a menudo por

\[g = \dfrac{g_0}{1 + \tfrac{I}{I_{sat}}}, \nonumber \]

donde\(I_{sat}\) está la intensidad de saturación. La saturación de ganancia es responsable de la ganancia en estado estacionario (ver Figura 1.11), y se asume una ganancia homogéneamente ensanchada.

Para generar pulsos cortos, es decir, más cortos que el tiempo de ida y vuelta de la cavidad, deseamos tener muchos modos longitudinales funcionando en estado estacionario. Para un láser multimodo, el campo láser viene dado por

\[E(z, t) = \Re \left [ \sum_{m} \hat{E}_m e^{j(\omega_m t - k_m z + \phi_m)} \right ], \nonumber \]

\[\omega_m = \omega_0 + m \Delta \omega = \omega_0 + \dfrac{m\pi c}{\ell}, \nonumber \]

\[k_m = \dfrac{\omega_m}{c}, \nonumber \]

donde el símbolo\(\hat{\ }\) denotesa cantidad de dominio de frecuencia. La ecuación (1.4.10) se puede reescribir como

\[E(z,t) = \Re \left \{e^{j \omega_0 (t - z/c) \sum_m \hat{E}_m e^{j (m \Delta \omega (t - z/c) + \phi_m)} \right\} \nonumber \]

\[= \Re [A(t - z/c) e^{j\omega_0 (t - z/c)} ] \nonumber \]

con la envolvente compleja

\[A(t - \dfrac{z}{c}) = \sum_m E_m e^{j (m \Delta \omega (t - z/c) + \phi_m)} = \text{complex envelope (slowly varying).} \nonumber \]

\(e^{j\omega_0 (t - z/c)\)es la onda portadora (oscilación rápida). Tanto el portador como el sobre viajan con la misma velocidad (no se supone dispersión). La función envolvente es periódica con punto

\[T = \dfrac{2\pi}{\Delta \omega} = \dfrac{2\ell}{c} = \dfrac{L}{c}. \nonumber \]

\(L\)es la longitud de ida y vuelta (óptica)!

Ejemplo\(\PageIndex{1}\)

Asumimos\(N\) modos con amplitudes iguales\(E_m = E_0\) y fases iguales\(\phi_m = 0\), y así la envolvente viene dada por

\[A (z, t) = E_0 \sum_{m = -(N-1)/2}^{(N - 1)/2} e^{j(m \Delta \omega (t - z/c))} \nonumber \]

Con

\[\sum_{m = 0}^{q - 1} a^m = \dfrac{1 - a^q}{1 - a}, \nonumber \]

obtenemos

\[A(z, t) = E_0 \dfrac{\sin [\tfrac{N \Delta \omega}{2} ( t - \tfrac{z}{c})]}{\sin [\tfrac{\Delta \omega}{2} ( t - \tfrac{z}{c})]} \nonumber \]

La intensidad del láser\(I\) es proporcional a\(E(z,t)^2\), promediado sobre un ciclo óptico:\(I \sim |A(z, t)|^2\). En\(z = 0\), obtenemos

\[I(t) \sim |E_0|^2 \dfrac{\sin^2 (\tfrac{N \Delta \omega t}{2})}{\sin^2 (\tfrac{\Delta \omega t}{2})}. \nonumber \]

Figura 1.12: (a) salida láser de modo bloqueado con fase de modo constante. (b) Salida láser con modos de fase aleatoria.

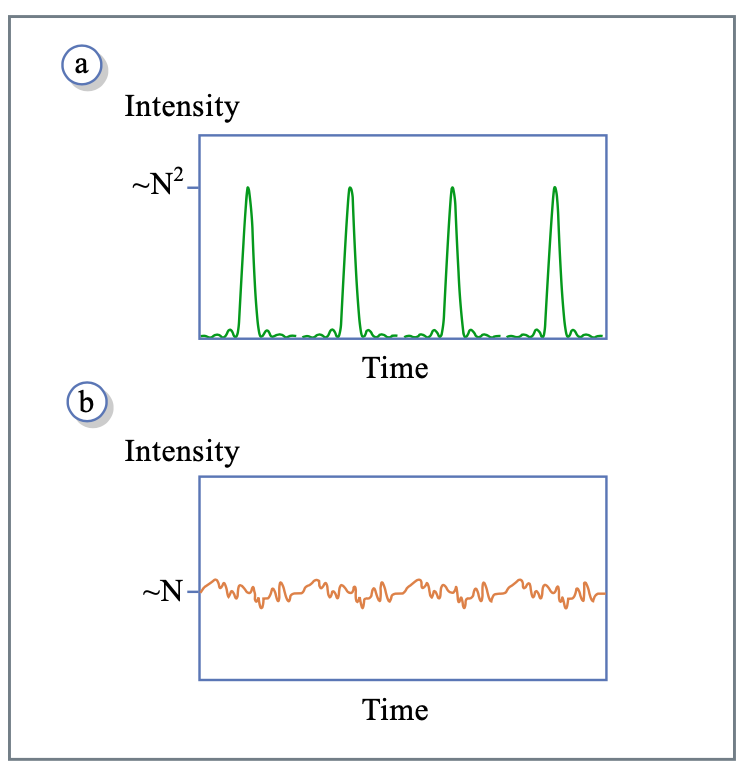
a) Pulsos periódicos dados por la Ecuación 1.4.19, periodo\(T = 1/ \Delta f = L/c\)

• duración del pulso

\[\Delta t = \dfrac{2\pi}{N \Delta \omega} = \dfrac{1}{N\Delta f} \nonumber \]

• intensidad pico ~\(N^2 |E_0|^2\)
• intensidad promedio ~ la intensidad\(N |E_0|^2 \Rightarrow\) máxima se ve potenciada por un factor\(N\).

(b) Si las fases de los modos no están bloqueadas, es decir, secuencia\(\phi_m\) aleatoria

• La intensidad fluctúa aleatoriamente alrededor del valor promedio (\(\sim N |E_0|^2\)), igual que el caso modelocked

• el tiempo de correlación es\(\Delta t_c \approx \dfrac{1}{N \cdot \Delta f}\)

• Las fluctuaciones siguen siendo periódicas con periodo\(T = 1/\Delta f\).

En un láser multimodo habitual,\(\phi_m\) varía sobre\(t\).