9.3: La decisión de abasto de la firma

El concepto de ingresos marginales es clave para analizar la decisión de oferta de una empresa individual. Hemos utilizado análisis marginales en varios puntos hasta la fecha. En la teoría del consumidor, vimos cómo los consumidores equilibran la utilidad por dólar al margen en la asignación de su presupuesto. Los ingresos marginales son los ingresos adicionales que se devengan a la firma por la venta de una unidad más de producción.

Los ingresos marginales son los ingresos adicionales que se devengan a la firma resultantes de la venta de una unidad más de producción.

En perfecta competencia, el ingreso marginal (MR) de una firma es el precio del bien. Dado que el precio es constante para el proveedor individual, cada unidad adicional que se vende al precio P genera los mismos ingresos adicionales. Por lo tanto, P = MR. Por ejemplo, si un negocio de tintorería lava 10 camisas o 100 camisas por día, el precio que se cobra a los clientes es el mismo. Esta igualdad no se mantiene en ninguna otra estructura de mercado, como veremos en los capítulos siguientes.

Abastecimiento a corto plazo

Recordemos cómo definimos el corto plazo en el capítulo anterior: El tamaño de planta de cada firma es fijo a corto plazo, así también lo es el número de firmas en una industria. A la larga, cada firma individual puede cambiar su escala de operación, y al mismo tiempo pueden ingresar nuevas firmas o las firmas existentes pueden salir de la industria.

Los proveedores perfectamente competitivos enfrentan la elección de cuánto producir al precio de mercado en marcha: es decir, la cantidad que maximizará su ganancia. Abstrayamos por el momento cómo se determina el precio en el mercado. Veremos más adelante en este capítulo que emerge como el valor correspondiente a la intersección de las curvas de oferta y demanda para todo el mercado —como se describe en el Capítulo 3.

La curva MC de la firma es crítica para definir la cantidad óptima a abastecer a cualquier precio. En la Figura 9.1, el MC es la curva de costo marginal de la firma a corto plazo. Al precio la cantidad óptima para abastecer es, la cantidad determinada por la intersección del MC y la demanda. Para ver por qué, imagina que el productor optó por abastecer la cantidad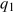. Tal producción dejaría sin explotar la oportunidad de obtener mayores ganancias. Al producir una unidad adicional más allá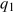, el proveedor obtendría ingresos adicionales e incurriría en un costo adicional que es menor que en la producción de esta unidad. De hecho, en cada unidad entre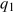 y puede obtener ganancias, porque el MR supera el costo asociado, MC. Por el mismo argumento, no tiene sentido aumentar la producción más allá, por ejemplo, porque el costo de dichas unidades adicionales de producción, MC, supera los ingresos de ellas. Por lo tanto, el MC define una respuesta óptima de suministro.

Figura 9.1 El rendimiento óptimo de la empresa competitiva

Aquí, q ₀ representa la decisión óptima de suministro cuando el precio es P ₀. A la salida q ₁ el costo de las unidades adicionales es menor que el ingreso de dichas unidades y por lo tanto es rentable aumentar la producción más allá de q ₁. Por el contrario, a q ₂ el MC de producción supera los ingresos obtenidos, por lo que se debe reducir la producción.

Aplicación Casilla 9.1 La ley de un precio

Si la información no fluye, entonces los precios en diferentes partes de un mercado pueden diferir y los posibles participantes pueden no saber ingresar a un mercado rentable.

Considere a los pescadores frente a la costa de Kerala, India a finales de los noventa. Su mercado fue estudiado por Robert Jensen, economista del desarrollo. Antes de 1997, los pescadores tendían a llevar sus peces a su mercado o puerto de origen. Esto era más barato que aventurarse a otros puertos, sobre todo si no había certeza en cuanto al precio. Esta práctica resultó en precios altos en algunos mercados locales y bajos en otros, dependiendo de la captura diaria. Frecuentemente el pescado se tiraba en los mercados de bajo precio a pesar de que podría haber encontrado un precio favorable en el mercado de pescado de otro pueblo.

Todo esto cambió con la llegada de los celulares. En lugar de dirigirse automáticamente a su puerto de origen, los pescadores comenzaron a llamar por teléfono a varios mercados diferentes con la esperanza de encontrar un buen precio por sus esfuerzos. Empezaron a formar acuerdos con los compradores antes incluso de llevar su captura a puerto. El economista Jensen observó una importante disminución en la variación de precios entre los mercados que encuestó. En efecto, la 'ley de un precio' nació para las sardinas como resultado de la introducción de tecnología barata y el flujo relativamente libre de información.

Si bien la elección de la salida es la mejor opción para el productor, la Figura 9.1 no nos dice nada sobre las ganancias. Para eso necesitamos más información sobre costos. En consecuencia, en la Figura 9.2 las curvas AVC y ATC de la firma se han agregado a la Figura 9.1. Como se explicó en el capítulo anterior, la curva ATC incluye componentes de costos fijos y variables, y la curva MC corta el AVC y el ATC en sus mínimos.

Figura 9.2 Suministro a corto plazo para la firma competitiva

Un precio por debajo de P ₁ no cubre costos variables, por lo que la firma debe cerrar. Entre los precios P ₁ y P ₃, el productor puede cubrir costos variables, pero no totales, y por lo tanto debería producir a corto plazo si los costos fijos son 'hundidos'. A la larga la firma debe cerrar si el precio no llega a P ₃. Se obtienen ganancias si el precio supera P ₃. La curva de oferta a corto plazo es la cantidad suministrada a cada precio. Por lo tanto, es la curva MC por encima de P ₁.

En primer lugar, señalar que cualquier precio por debajo, que corresponde al mínimo de la curva ATC, no produce ganancias, ya que no permite al productor cubrir todos sus costos. Por lo tanto, este precio se llama el precio de equilibrio. Segundo, cualquier precio por debajo, que corresponda al mínimo del CVA, ni siquiera permite al productor cubrir costos variables. ¿Qué pasa con un precio como, que se encuentra entre estos? La respuesta es que, si el proveedor ya ha incurrido en algunos costos fijos, debe seguir produciendo, siempre que pueda cubrir su costo variable. Pero a la larga debe cubrir todos sus costos, fijos y variables. Por lo tanto, si el precio cae por debajo, debería cerrar, incluso a corto plazo. Por lo tanto, este precio se llama el precio de cierre. Si un precio al menos igual a no puede sostenerse a largo plazo, debería abandonar la industria. Pero a un precio como él puede cubrir costos variables y por lo tanto debería seguir produciendo a corto plazo. Su salida óptima en está definida por la intersección de la línea con la curva MC. La curva de oferta a corto plazo de la empresa es, por lo tanto, esa porción de la curva MC por encima del mínimo del AVC.

Para ilustrar esto más concretamente, considere nuevamente el ejemplo de nuestro productor de snowboard, e imagine que está produciendo en un mercado perfectamente competitivo. ¿Cómo debe comportarse ante diferentes precios? En el Cuadro 9.1 se reproducen los datos del Cuadro 8.2.

Tabla 9.1 Maximización de beneficios a corto plazo

Laboral	Salida	Total	Promedio	Promedio	Marginal	Total	Beneficio
		Ingresos $	Variable	Costo Total	Costo $	Costo $
			Costo	$
L	Q	TR	CVA	ATC	MC	TC	TR-TC
0	0					3,000
1	15	1,050	66.67	266.67	66.67	4,000	—2,950
2	40	2,800	50.0	125.0	40.0	5,000	—2,200
3	70	4,900	42.86	85.71	33.33	6,000	—1,100
4	110	7,700	36.36	63.64	25.0	7,000	700
5	145	10,150	34.48	55.17	28.57	8,000	2,150
6	175	12,250	34.29	51.43	33.33	9,000	3,250
7	200	14,000	35.0	50.0	40.0	10,000	4,000
8	220	15,400	36.36	50.0	50.0	11,000	4,400
9	235	16,450	38.30	51.06	66.67	12,000	4,450
10	240	16,800	41.67	54.17	200.0	13,000	3,800

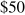
Precio de salida=$70; Salario = $1,000; Costo Fijo=$3,000. El punto de cierre se produce a un precio de, donde el CVA alcanza un mínimo. De ahí que no se produzca ninguna producción, ni siquiera a corto plazo, a menos que el precio rebase este valor. El nivel de equilibrio de salida se produce a un precio de, donde el ATC alcanza un mínimo.

El precio de cierre corresponde al valor mínimo de la curva AVC.

El precio de equilibrio corresponde al mínimo de la curva ATC.

La curva de oferta a corto plazo de la empresa es aquella porción de la curva MC por encima del mínimo del AVC.

Supongamos que el precio es de 70 dólares. ¿Cuántas tablas debería producir? La respuesta se define por el comportamiento de la curva MC. Para cualquier salida menor o igual a 235, el MC es menor que el precio. Por ejemplo, a L =9 y Q =235, el MC es de $66.67. A este nivel de producción, obtiene ganancias sobre la unidad marginal producida, porque el MC es menor que los ingresos que obtiene (70 dólares) por venderlo.

Pero, a salidas por encima de esto, registra una pérdida sobre las unidades marginales porque el MC supera los ingresos. Por ejemplo, a L =10 y Q =240, el MC es de $200. Claramente, 235 tablas de snowboard es lo óptimo. Producir más generaría una pérdida en cada unidad adicional, debido a que el costo adicional superaría los ingresos adicionales. Además, producir menos tablas de snowboard significaría no aprovechar el potencial de ganancias en tablas adicionales.

Su ganancia se basa en la diferencia entre ingresos por unidad y costo por unidad a esta salida: (P — ATC). Dado que el ATC para las 235 unidades producidas por los nueve trabajadores es de 51.06 dólares, su margen de beneficio es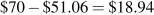 por junta, y la ganancia total es por lo tanto.

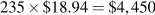Establezcamos otras dos salidas clave y precios para el productor. Primero, el punto de cierre es el mínimo de su curva CVA. El Cuadro 9.1 indica que el precio debe ser de al menos $34.29 para que esté dispuesto a abastecer cualquier salida, ya que ese es el valor del AVC en su mínimo. Segundo, el mínimo de su ATC está en $50. En consecuencia, siempre que el precio supere los $50, cubrirá tanto los costos variables como los fijos y obtendrá una ganancia máxima cuando elija una salida donde P = MC, arriba. De ello se deduce que la curva de oferta a corto plazo para Black Diamond Snowboards es el segmento de la curva MC en la Figura 8.4 por encima de la curva AVC.

Dado que hemos desarrollado la curva de oferta de la firma individual, la siguiente tarea es desarrollar la curva de oferta de la industria.

Abastecimiento de la industria a corto plazo

En el Capítulo 3 se demostró que las demandas individuales pueden agregarse a una demanda de la industria sumarlas horizontalmente. La oferta de la industria se obtiene exactamente de la misma manera, al sumar las cantidades de suministro de las empresas en todas las firmas de la industria.

Para ilustrar, imaginemos que tenemos muchas firmas, posiblemente operando a diferentes escalas de producción y por lo tanto teniendo diferentes curvas MC de corto plazo. Las curvas MC de dos de estas firmas se ilustran en la Figura 9.3. El MC de A está por debajo del MC de B; por lo tanto, B probablemente tenga una escala de planta menor que A. Considere primero las decisiones de suministro en el rango de precios P ₁ a P ₂. A cualquier precio entre estos límites, solo la firma A suministrará producción — la firma B no cubre su AVC en este rango de precios. Por lo tanto, la contribución conjunta a la oferta industrial de las firmas A y B viene dada por la curva MC de la firma A. Pero una vez que se alcanza un precio de P ₂, la firma B ahora está dispuesta a abastecer. El horario es la suma horizontal de sus cantidades de suministro. Al sumar los suministros de todas las firmas de la industria de esta manera se obtiene la oferta de la industria.

La oferta de la industria (tirada corta) en perfecta competencia es la suma horizontal de las curvas de oferta de todas las empresas.

Figura 9.3 Derivando el suministro de la industria

Las curvas de costos marginales para las firmas A y B indican que a cualquier precio por debajo de P ₁ la producción no es rentable y, por lo tanto, la oferta es cero para ambas firmas. A precios entre P ₁ y P ₂ la firma A está dispuesta a abastecer, pero no la firma B. En consecuencia, la oferta del mercado proviene únicamente de A. A precios superiores a P ₂ ambas firmas están dispuestas a abastecer. Por lo tanto, la oferta del mercado es la suma horizontal de la oferta de cada empresa.

Equilibrio de la industria

Consideremos a continuación el equilibrio de la industria. Dado que la oferta de la industria es la suma de los suministros individuales, y la curva de demanda de la industria es la suma de las demandas individuales, un precio de equilibrio y cantidad (P _E, Q _E) se definen por la intersección de estos a nivel de industria curvas, como en la Figura 9.4. Aquí, cada firma toma P _E como se da (es tan pequeña que no puede influir en el precio que va), y abastece una cantidad determinada por la intersección de este precio con su curva MC. Por lo tanto, la suma de tales cantidades es Q _E.

El equilibrio a corto plazo en perfecta competencia ocurre cuando cada empresa maximiza el beneficio al producir una cantidad donde P = MC, siempre que el precio supere el mínimo del costo variable promedio.

Figura 9.4 Equilibrio del mercado

La curva de oferta del mercado S es la suma de la curva de oferta o MC de cada empresa por encima del precio de cierre. D es la suma de las demandas individuales. El precio de equilibrio del mercado y la cantidad están definidos por P _E y Q _E.