Ahora hemos descrito el equilibrio de mercado y nivel de empresa a corto plazo. Sin embargo, este equilibrio puede ser sólo temporal; si se puede sostener o no depende de si se están incurriendo en ganancias (o pérdidas), o de si todas las firmas participantes están obteniendo lo que se denomina ganancias normales. Dichos beneficios se consideran parte esencial de la operación de una empresa. Reflejan el costo de oportunidad de los recursos utilizados en la producción. Las empresas no operan si no pueden obtener un nivel de ganancias mínimo o normal. Por encima de tales ganancias están las ganancias económicas (también llamadas ganancias supernormales), y estas son las que atraen la entrada a la industria.
Recordemos del Capítulo 7 que las ganancias contables y económicas son diferentes. El economista incluye los costos de oportunidad en la determinación de ganancias, mientras que el contador considera los ingresos y costos reales. En el ejemplo desarrollado en la Sección 7.2 el empresario registró el beneficio contable, pero no el beneficio económico. Supongamos ahora que los números eran ligeramente diferentes, y son como se definen en el Cuadro 9.2: Felicity invierte 250.000 dólares en su negocio en forma de capital, como antes. Pero ahora tiene ingresos brutos de 165,000 dólares e incurre en un costo de 90.000 dólares para comprar la ropa al por mayor que luego vende al por menor. Ella se paga a sí misma un salario de 35 mil dólares. Si estos números representan su balance, entonces ella registra una ganancia contable de 40,000 dólares.
Cuadro 9.2 Ganancias económicas
| Ventas |
|
$165,000 |
| Costos de materiales |
|
$90,000 |
| Costos salariales |
|
$35,000 |
| Beneficio contable |
|
$40.000 |
| Capital invertido |
250,000 |
|
| Rentabilidad implícita sobre el capital al 4% |
|
$10,000 |
| Costos salariales implícitos adicionales |
|
$20,000 |
| Costos totales implícitos |
|
$30,000 |
| Beneficio económico |
|
$10,000 |
Su cálculo de ganancias económicas debe incluir costos de oportunidad. El costo de oportunidad de amarrar $250,000 de capital, si la tasa de interés es del 4%, asciende a $10,000. Además, si Felicity pudiera ganar 55,000 dólares en su mejor trabajo alternativo entonces se debe considerar un costo implícito adicional de 20,000 dólares. Cuando estos dos costos de oportunidad (o implícitos) se agregan al balance general, su ganancia se reduce a 10,000 dólares. Esta es su ganancia económica. Si el beneficio económico de Felicity es representativo del sector minorista de la confección de la economía, entonces esa rentabilidad debería atraer a nuevos emprendedores. Nuestra conclusión es que este sector de la economía debería experimentar nuevos entrantes y de ahí un desplazamiento hacia afuera de la curva de oferta. En contraste, en el ejemplo numérico considerado en la Sección 7.2, Felicity estaba experimentando pérdidas (ganancias económicas negativas), y a más largo plazo tendría que considerar abandonar el negocio. Si ella y otros proveedores salieran, entonces la curva de oferta del mercado se desplazaría hacia la izquierda, lo que representa una reducción en la oferta.
El punto crítico en esta distinción entre contabilidad y costo económico es que la decisión de entrar o salir de un mercado a largo plazo se basa en lo que el empresario puede ganar en el mercado más amplio. Es decir, las ganancias económicas más que las ganancias contables determinarán el número de equilibrio de las empresas a largo plazo. En cuanto a nuestras curvas de costos, asumiremos que los costos económicos completos están incluidos en las diversas curvas que utilizamos. En consecuencia, las ganancias (o pérdidas) que surjan se basan en la totalidad de los costos económicos de la operación de la firma.
Las ganancias económicas (supernormales) son aquellas utilidades por encima de las normales que inducen a las empresas a ingresar a una industria.
Volvamos a nuestro análisis gráfico, y comencemos suponiendo que el equilibrio de mercado descrito en la Figura 9.4 da como resultado que algunas empresas obtengan beneficios. Tal resultado se describe en la Figura 9.5, donde el precio supera al ATC. Al precio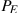
, una firma lucrativa suministra la cantidad
, según lo determinado por su curva MC. En promedio, el costo de producir cada unidad de producción,, se define por el punto en el ATC a ese nivel de salida, punto k. El beneficio por unidad viene dado así por el valor (m — k) — la diferencia entre ingresos por unidad y costo por unidad. El beneficio total (económico) es por lo tanto el área
, que es cantidad veces ganancia por unidad.
Si bien representa un equilibrio para la empresa, solo es un equilibrio a corto plazo, o temporal, para la industria. El supuesto de entrada y salida libres implica que la presencia de ganancias económicas inducirá a nuevos empresarios a entrar y comenzar a producir. El impacto de esta dinámica se ilustra en la Figura 9.6. Un mayor número de firmas desplaza la oferta hacia la derecha para convertirse
, incrementando así la cantidad suministrada a cualquier precio. El impacto en el precio de este cambio de oferta es evidente: Con una demanda sin cambios, el precio de equilibrio debe caer.
¿Hasta dónde bajará el precio y cuántas firmas nuevas entrarán en esta rentable industria? Mientras existan ganancias económicas entrarán nuevas firmas y el incremento resultante en la oferta seguirá impulsando el precio a la baja. Pero, una vez que el precio se ha bajado al mínimo del ATC de una firma representativa, ya no hay un incentivo para que ingresen nuevos empresarios. Por lo tanto, el equilibrio de la industria a largo plazo es donde el precio de mercado es igual al punto mínimo de la curva ATC de una empresa. Esto genera ganancias normales, y no hay incentivo para que las empresas entren o salgan.
Un equilibrio a largo plazo en una industria competitiva requiere un precio igual al punto mínimo del ATC de una empresa. En este punto, solo existen ganancias normales, y no hay incentivo para que las empresas entren o salgan.
Al desarrollar esta dinámica, comenzamos con una situación en la que las ganancias económicas estaban presentes. No obstante, podríamos haber arrancado igualmente desde una posición de pérdidas. Con un precio de mercado entre el mínimo del CVA y el mínimo del ATC en la Figura 9.5, los ingresos por unidad superarían los costos variables pero no los costos totales por unidad. Cuando las empresas no puedan cubrir su ATC a largo plazo, cesarán la producción. Dichos cierres deben reducir la oferta agregada; en consecuencia, la curva de oferta del mercado se contrae, en lugar de expandirse como lo hizo en la Figura 9.6. El suministro reducido eleva el precio del bien. Este proceso continúa mientras las empresas estén haciendo pérdidas. Un equilibrio final de la industria se alcanza sólo cuando el precio alcanza un nivel en el que las empresas pueden obtener un beneficio normal. Nuevamente, esto será al mínimo del ATC de la firma típica.
En consecuencia, el equilibrio a largo plazo es el mismo, independientemente de si partimos de una posición en la que las empresas están incurriendo en pérdidas, o donde están obteniendo ganancias.
Caja de Aplicación 9.2 Entrada y salida: plataformas petrolíferas
La perforación petrolera es un mercado competitivo. Hay un gran número de proveedores, la información es ubicua y la entrada y salida son relativamente libres.
En los años 2012 y 2013 el precio del crudo rondaba los 100 dólares estadounidenses por barril. Hacia finales de 2014 el precio del petróleo comenzó a caer en los mercados mundiales, y a principios de 2015 fluctuó alrededor de los 50 dólares. La respuesta de los perforadores en Estados Unidos fue sustancial e inmediata. El número de plataformas activas disminuyó drásticamente. En cuanto a nuestro modelo económico, ciertos proveedores salieron; hicieron bolas de polilla sus plataformas y esperaron a que se recuperara el precio del petróleo.
Otro de esos ciclos, aún más pronunciado, ocurrió en 2020. Con la pandemia de coronavirus, la demanda de petróleo bajó y su precio se desplomó. Nuevamente, muchas firmas cerraron sus plataformas y no tuvieron más remedio que dejar de lado la caída de los precios. Un gráfico altamente informativo se presenta en https://tradingeconomics.com/united-states/crude-oil-rigs.
Además de la disminución de las plataformas tradicionales de recuperación de petróleo, el número de equipos operativos de esquisto disminuyó en cantidades aún mayores. Detalles en https://www.forbes.com/sites/davidblackmon/2020/05/12/a-grim-earnings-season-for-the-us-shale-business/#6f55a95a1cf2
mk= TR — TC.
y el precio de equilibrio cae a
. La entrada continúa mientras estén presentes las ganancias económicas. Eventualmente el precio es conducido a un nivel donde solo se obtienen ganancias normales, y cesa la entrada.