6.3: Investigación correlacional

Objetivos de aprendizaje

1. Definir la investigación correlacional y dar varios ejemplos.
2. Explique por qué un investigador podría optar por realizar investigaciones correlacionales en lugar de investigaciones experimentales u otro tipo de investigación no experimental.
3. Interpretar la fuerza y dirección de diferentes coeficientes de correlación.
4. Explicar por qué la correlación no implica causalidad.

¿Qué es la investigación correlacional?

La investigación correlacional es un tipo de investigación no experimental en la que el investigador mide dos variables (binarias o continuas) y evalúa la relación estadística (es decir, la correlación) entre ellas con poco o ningún esfuerzo para controlar variables extrañas. Hay muchas razones por las que los investigadores interesados en las relaciones estadísticas entre variables elegirían realizar un estudio correlacional en lugar de un experimento. La primera es que no creen que la relación estadística sea causal o no estén interesados en las relaciones causales. Recordemos que dos objetivos de la ciencia son describir y predecir y la estrategia de investigación correlacional permite a los investigadores lograr ambos objetivos. Específicamente, esta estrategia puede ser utilizada para describir la fuerza y dirección de la relación entre dos variables y si existe una relación entre las variables entonces los investigadores pueden usar puntajes en una variable para predecir puntuaciones en la otra (utilizando una técnica estadística llamada regresión, que se discute más a fondo en la sección sobre Correlación Compleja en este capítulo).

Otra razón por la que los investigadores elegirían utilizar un estudio correlacional en lugar de un experimento es que se piensa que la relación estadística de interés es causal, pero el investigador no puede manipular la variable independiente porque es imposible, poco práctica, o poco ético. Por ejemplo, si bien un investigador podría estar interesado en la relación entre la frecuencia en que las personas usan cannabis y sus habilidades de memoria, no pueden manipular éticamente la frecuencia con la que las personas consumen cannabis. Como tal, deben confiar en la estrategia de investigación correlacional; simplemente deben medir la frecuencia con que las personas consumen cannabis y medir sus habilidades de memoria usando una prueba estandarizada de memoria para luego determinar si la frecuencia que las personas usan cannabis está estadísticamente relacionada con el rendimiento de las pruebas de memoria.

También se utiliza la correlación para establecer la confiabilidad y validez de las mediciones. Por ejemplo, un investigador podría evaluar la validez de una prueba breve de extraversión administrándola a un gran grupo de participantes junto con una prueba de extraversión más larga que ya se ha demostrado que es válida. Este investigador podría entonces verificar si las puntuaciones de los participantes en la prueba breve están fuertemente correlacionadas con sus puntuaciones en la más larga. Tampoco se piensa que el puntaje de la prueba cause al otro, por lo que no hay una variable independiente para manipular. De hecho, los términos variable independiente y variable dependiente no se aplican a este tipo de investigación.

Otra fortaleza de la investigación correlacional es que a menudo es mayor en validez externa que la investigación experimental. Recordemos que normalmente hay una compensación entre la validez interna y la validez externa. A medida que se agregan mayores controles a los experimentos, se incrementa la validez interna pero muchas veces a expensas de la validez externa ya que se introducen condiciones artificiales que no existen en la realidad. Por el contrario, los estudios correlacionales suelen tener baja validez interna porque no se manipula ni controla nada pero a menudo tienen una validez externa alta. Dado que nada es manipulado o controlado por el experimentador, es más probable que los resultados reflejen las relaciones que existen en el mundo real.

Finalmente, extendiendo sobre este equilibrio entre validez interna y externa, la investigación correlacional puede ayudar a proporcionar evidencia convergente para una teoría. Si una teoría es apoyada por un verdadero experimento que es alto en validez interna así como por un estudio correlacional que es alto en validez externa entonces los investigadores pueden tener más confianza en la validez de su teoría. Como ejemplo concreto, estudios correlacionales que establecen que existe una relación entre ver televisión violenta y comportamiento agresivo se han complementado con estudios experimentales que confirman que la relación es causal (Bushman & Huesmann, 2001) ^[1] .

¿La investigación correlacional siempre involucra variables cuantitativas?

Un error común entre los investigadores principiantes es que la investigación correlacional debe involucrar dos variables cuantitativas, como los puntajes en dos pruebas de extraversión o el número de molestias diarias y el número de síntomas que las personas han experimentado. Sin embargo, la característica definitoria de la investigación correlacional es que las dos variables se miden, ninguna de ellas es manipulada, y esto es cierto independientemente de que las variables sean cuantitativas o categóricas. Imagínese, por ejemplo, que un investigador administre la Escala de Autoestima de Rosenberg a 50 estudiantes universitarios estadounidenses y 50 estudiantes universitarios japoneses. Aunque esto “se siente” como un experimento entre sujetos, se trata de un estudio correlacional porque el investigador no manipuló las nacionalidades de los estudiantes. Lo mismo ocurre con el estudio de Cacioppo y Petty comparando a profesores universitarios y trabajadores de fábricas en términos de su necesidad de cognición. Se trata de un estudio correlacional porque los investigadores no manipularon las ocupaciones de los participantes.

La figura\(\PageIndex{1}\) muestra datos de un estudio hipotético sobre la relación entre si las personas hacen una lista diaria de cosas que hacer (una “lista de tareas pendientes”) y el estrés. Observe que no está claro si se trata de un experimento o de un estudio correlacional porque no está claro si la variable independiente fue manipulada. Si el investigador asignó aleatoriamente a algunos participantes a hacer listas diarias de tareas pendientes y a otros no, entonces es un experimento. Si el investigador simplemente preguntó a los participantes si hacían listas diarias de tareas pendientes, entonces se trata de un estudio correlacional. La distinción es importante porque si el estudio fue un experimento, entonces se podría concluir que hacer las listas diarias de tareas pendientes redujo el estrés de los participantes. Pero si se trataba de un estudio correlacional, sólo se podría concluir que estas variables están estadísticamente relacionadas. Quizás estar estresado tiene un efecto negativo en la capacidad de las personas para planificar con anticipación (el problema de la direccionalidad). O tal vez las personas que son más concienzudas tienen más probabilidades de hacer listas de tareas pendientes y menos propensas a ser estresadas (el problema de la tercera variable). El punto crucial es que lo que define a un estudio como experimental o correlacional no son las variables que se estudian, ni si las variables son cuantitativas o categóricas, ni el tipo de gráfica o estadística utilizada para analizar los datos. Lo que define un estudio es cómo se realiza el estudio.

Figura\(\PageIndex{1}\): Resultados de un estudio hipotético sobre si las personas que hacen listas diarias de tareas pendientes experimentan menos estrés que las personas que no hacen tales listas

Recogida de datos en la investigación correlacional

Nuevamente, la característica definitoria de la investigación correlacional es que ninguna de las variables es manipulada. No importa cómo ni dónde se midan las variables. Un investigador podría hacer que los participantes vinieran a un laboratorio para completar una tarea computarizada de lapso de dígitos hacia atrás y una tarea de toma de decisiones arriesgada computarizada y luego evaluar la relación entre las puntuaciones de los participantes en las dos tareas. O un investigador podría ir a un centro comercial para preguntar a la gente sobre sus actitudes hacia el medio ambiente y sus hábitos de compra y luego evaluar la relación entre estas dos variables. Ambos estudios serían correlacionales porque no se manipula ninguna variable independiente.

diagramas de dispersión. La figura\(\PageIndex{2}\) muestra algunos datos hipotéticos sobre la relación entre la cantidad de estrés que sufren las personas y el número de síntomas físicos que tienen. Cada punto en la gráfica de dispersión representa la puntuación de una persona en ambas variables. Por ejemplo, el punto circular en la Figura\(\PageIndex{2}\) representa a una persona cuya puntuación de estrés fue de 10 y que presentaba tres síntomas físicos. Teniendo en cuenta todos los puntos, se puede ver que las personas bajo más estrés tienden a tener más síntomas físicos. Este es un buen ejemplo de una relación positiva, en la que las puntuaciones más altas en una variable tienden a asociarse con puntuaciones más altas en la otra. Es decir, se mueven en la misma dirección, ya sea ambos hacia arriba o ambos hacia abajo. Una relación negativa es aquella en la que las puntuaciones más altas en una variable tienden a asociarse con puntuaciones más bajas en la otra. En otras palabras, se mueven en direcciones opuestas. Existe una relación negativa entre el estrés y el funcionamiento del sistema inmunológico, por ejemplo, debido a que un mayor estrés se asocia con un menor funcionamiento del sistema inmunológico.

Figura\(\PageIndex{2}\): Gráfica de dispersión que muestra una relación hipotética positiva entre estrés y número de síntomas físicos. El punto circular representa a una persona cuyo puntaje de estrés fue de 10 y que presentó tres síntomas físicos. La r de Pearson para estos datos es +.51.

La fuerza de una correlación entre variables cuantitativas se mide típicamente usando un estadístico llamado Coeficiente de Correlación de Pearson (o r de Pearson). Como\(\PageIndex{3}\) muestra la Figura, la r de Pearson varía de −1.00 (la relación negativa más fuerte posible) a +1.00 (la relación positiva más fuerte posible). Un valor de 0 significa que no hay relación entre las dos variables. Cuando r de Pearson es 0, los puntos en una gráfica de dispersión forman una “nube” sin forma. A medida que su valor se mueve hacia −1.00 o +1.00, los puntos se acercan cada vez más a caer sobre una sola línea recta. Los coeficientes de correlación cercanos a ±.10 se consideran pequeños, los valores cercanos a ± .30 se consideran medios y los valores cercanos a ±.50 se consideran grandes. Observe que el signo de la r de Pearson no está relacionado con su fuerza. Los valores r de Pearson de +.30 y −.30, por ejemplo, son igualmente fuertes; es solo que uno representa una relación positiva moderada y el otro una relación negativa moderada. A excepción de los coeficientes de confiabilidad, la mayoría de las correlaciones que encontramos en Psicología son de tamaño pequeño o moderado. El sitio web http://rpsychologist.com/d3/correlation/, creado por Kristoffer Magnusson, proporciona una excelente visualización interactiva de correlaciones que le permite ajustar la fuerza y dirección de una correlación mientras se presencian los cambios correspondientes en la trama de dispersión.

Figura\(\PageIndex{3}\): Rango de r de Pearson, desde −1.00 (relación negativa más fuerte posible), pasando por 0 (sin relación), hasta +1.00 (relación positiva más fuerte posible)

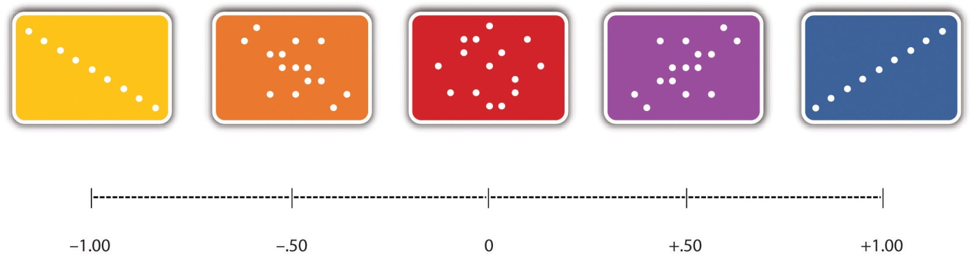
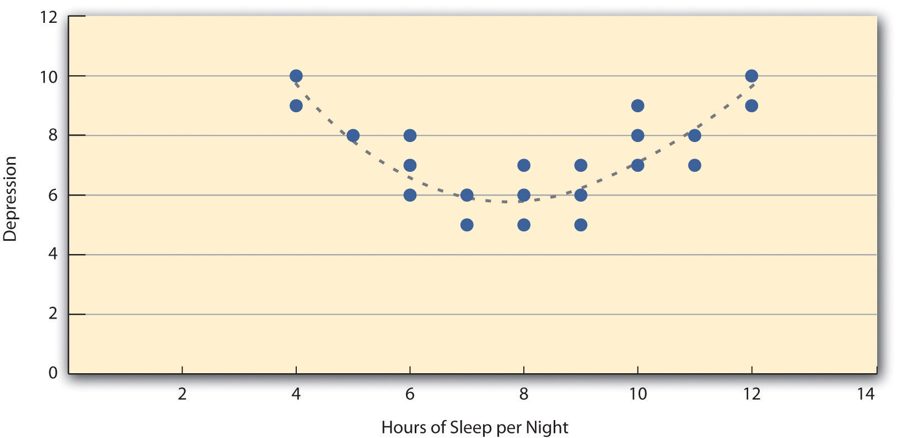
Hay dos situaciones comunes en las que el valor de r de Pearson puede ser engañoso. La r de Pearson es una buena medida solo para las relaciones lineales, en las que los puntos se aproximan mejor por una línea recta. No es una buena medida para las relaciones no lineales, en las que los puntos se aproximan mejor por una línea curva. La figura\(\PageIndex{4}\), por ejemplo, muestra una relación hipotética entre la cantidad de sueño que las personas duermen por noche y su nivel de depresión. En este ejemplo, la línea que mejor se aproxima a los puntos es una curva —una especie de “U” al revés— porque las personas que duermen alrededor de ocho horas tienden a ser las menos deprimidas. Los que duermen muy poco y los que duermen demasiado tienden a estar más deprimidos. A pesar de que la Figura\(\PageIndex{4}\) muestra una relación bastante fuerte entre la depresión y el sueño, la r de Pearson estaría cerca de cero porque los puntos en la gráfica de dispersión no están bien ajustados por una sola línea recta. Esto significa que es importante hacer una gráfica de dispersión y confirmar que una relación es aproximadamente lineal antes de usar r de Pearson. Las relaciones no lineales son bastante comunes en psicología, pero medir su fuerza está más allá del alcance de este libro.

Figura\(\PageIndex{4}\): Relación hipotética no lineal entre sueño y depresión

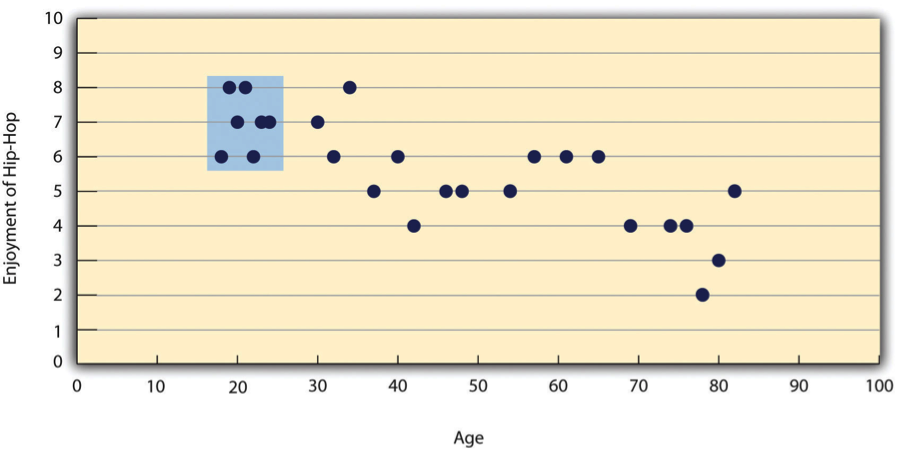
Las otras situaciones comunes en las que el valor de r de Pearson puede ser engañoso es cuando una o ambas variables tienen un rango limitado en la muestra en relación con la población. Este problema se conoce como restricción de rango. Supongamos, por ejemplo, que existe una fuerte correlación negativa entre la edad de las personas y su disfrute de la música hip hop como lo muestra la trama de dispersión de la Figura\(\PageIndex{5}\). La r de Pearson aquí es −.77. Sin embargo, si tuviéramos que recolectar datos solo de 18 a 24 años de edad, representados por el área sombreada de la\(\PageIndex{5}\) Figura, entonces la relación parecería ser bastante débil. De hecho, la r de Pearson para este rango restringido de edades es 0. Es una buena idea, por lo tanto, diseñar estudios para evitar la restricción de rango. Por ejemplo, si la edad es una de tus variables principales, entonces puedes planear recopilar datos de personas de un amplio rango de edades. Debido a que la restricción de rango no siempre se anticipa o se puede evitar fácilmente, sin embargo, es una buena práctica examinar sus datos en busca de una posible restricción de rango e interpretar la r de Pearson a la luz de ella. (También existen métodos estadísticos para corregir la r de Pearson para la restricción de rango, pero están más allá del alcance de este libro).

Figura\(\PageIndex{5}\): Datos hipotéticos que muestran cómo una correlación general fuerte puede parecer débil cuando una variable tiene un rango restringido. La correlación general aquí es −.77, pero la correlación para los jóvenes de 18 a 24 años (en el cuadro azul) es 0.

La correlación no implica causalidad

Probablemente hayas escuchado repetidamente que “La correlación no implica causalidad”. Un ejemplo divertido de esto proviene de un estudio de 2012 que mostró una correlación positiva (r = 0.79 de Pearson) entre el consumo per cápita de chocolate de una nación y el número de premios Nobel otorgados a ciudadanos de esa nación ^[2]. Parece claro, sin embargo, que esto no significa que comer chocolate haga que la gente gane premios Nobel, y no tendría sentido tratar de aumentar el número de premios Nobel ganados recomendando que los padres alimenten más chocolate a sus hijos.

Hay dos razones por las que la correlación no implica causalidad. El primero se llama el problema de la direccionalidad. Dos variables, X e Y, pueden relacionarse estadísticamente porque X causa Y o porque Y causa X. Consideremos, por ejemplo, un estudio que demuestre que si las personas hacen ejercicio o no está estadísticamente relacionado con lo felices que son, de tal manera que las personas que hacen ejercicio son más felices en promedio que las personas que no lo hacen. Esta relación estadística es consistente con la idea de que el ejercicio causa felicidad, pero también es consistente con la idea de que la felicidad causa ejercicio. Quizás ser feliz le da más energía a la gente o la lleve a buscar oportunidades para socializar con los demás al ir al gimnasio. La segunda razón por la que la correlación no implica causalidad se llama el problema de la tercera variable. Dos variables, X e Y, pueden estar estadísticamente relacionadas no porque X causa Y, o porque Y causa X, sino porque alguna tercera variable, Z, causa tanto X como Y. Por ejemplo, el hecho de que las naciones que han ganado más premios Nobel tienden a tener un mayor consumo de chocolate probablemente refleja geografía en que los países europeos tienden a tener tasas más altas de consumo per cápita de chocolate e invierten más en educación y tecnología (una vez más, per cápita) que muchos otros países en el mundo. De igual manera, la relación estadística entre el ejercicio y la felicidad podría significar que alguna tercera variable, como la salud física, cause las dos otras. Estar físicamente sano podría hacer que las personas hagan ejercicio y hacer que sean más felices. Las correlaciones que son el resultado de una tercera variable a menudo se denominan correlaciones espurias.

Algunos ejemplos excelentes y divertidos de correlaciones espurias se pueden encontrar en http://www.tylervigen.com (La figura\(\PageIndex{6}\) proporciona uno de esos ejemplos).

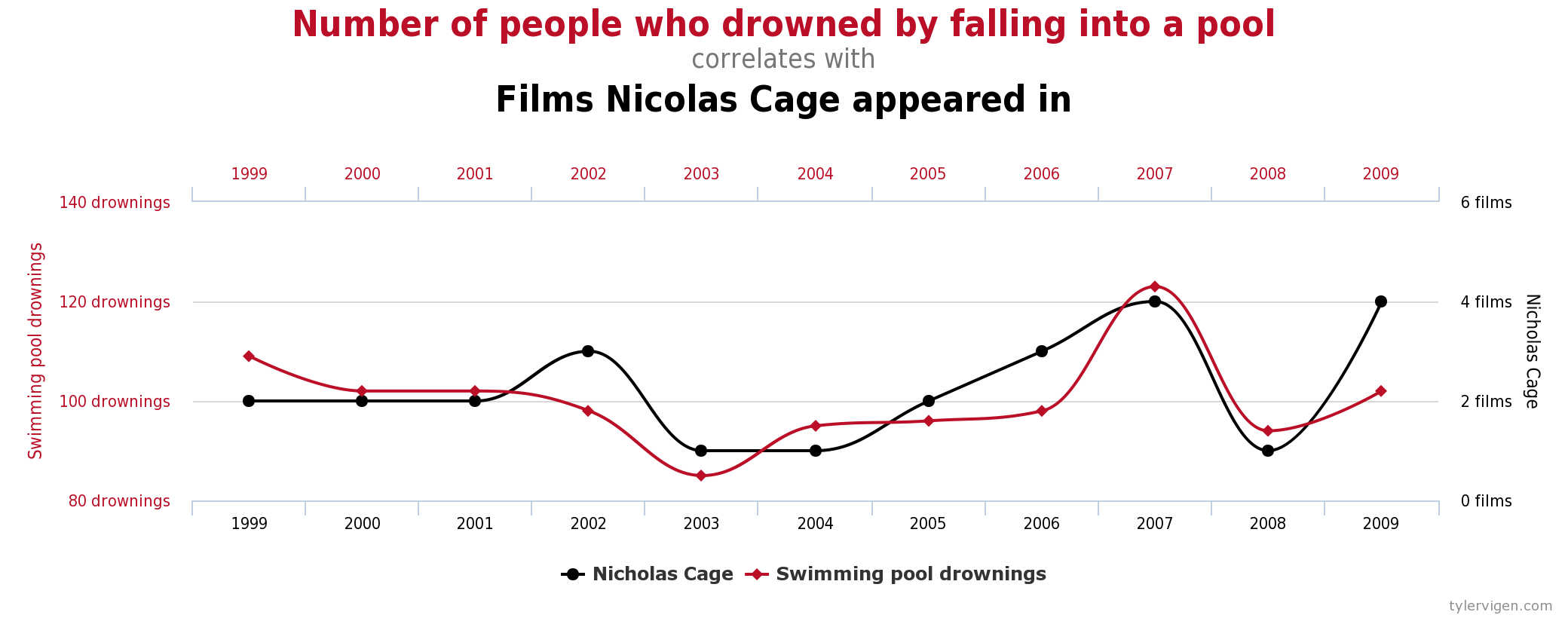Figura\(\PageIndex{6}\): Ejemplo de una Correlación Espuria. Fuente: http://tylervigen.com/spurious-correlations (CC-BY 4.0)

“Muchos dulces podrían conducir a la violencia”

Aunque los investigadores en psicología saben que la correlación no implica causalidad, muchos periodistas no lo hacen. Un sitio web sobre correlación y causalidad, http://jonathan.mueller.faculty.noctrl.edu/100/correlation_or_causation.htm, enlaces a decenas de reportajes mediáticos sobre investigaciones biomédicas y psicológicas reales. Muchos de los titulares sugieren que se ha demostrado una relación causal cuando una lectura cuidadosa de los artículos demuestra que no lo ha hecho por la direccionalidad y problemas de tercera variable.

Uno de esos artículos trata sobre un estudio que muestra que los niños que comían dulces todos los días tenían más probabilidades que otros niños de ser detenidos por un delito violento más adelante en la vida. Pero, ¿podrían realmente los dulces “conducir” a la violencia, como sugiere el titular? ¿Qué explicaciones alternativas se te ocurren para esta relación estadística? ¿Cómo podría reescribirse el titular para que no sea engañoso?

Como has aprendido al leer este libro, hay varias formas en que los investigadores abordan la direccionalidad y los problemas de tercera variable. Lo más efectivo es realizar un experimento. Por ejemplo, en lugar de simplemente medir cuánto hace ejercicio la gente, un investigador podría llevar a las personas a un laboratorio y asignar aleatoriamente la mitad de ellas para que corran en una cinta de correr durante 15 minutos y el resto para sentarse en un sofá durante 15 minutos. Si bien esto parece un cambio menor en el diseño de la investigación, es sumamente importante. Ahora bien, si los ejercitadores terminan en estados de ánimo más positivos que los que no hicieron ejercicio, no puede ser porque sus estados de ánimo afectaron lo mucho que ejercieron (porque fue el investigador quien utilizó la asignación aleatoria para determinar cuánto ejercieron). De igual manera, no puede ser porque alguna tercera variable (por ejemplo, la salud física) afectó tanto lo mucho que ejercieron como en qué estado de ánimo se encontraban. Así, los experimentos eliminan la direccionalidad y los problemas de tercera variable y permiten a los investigadores sacar conclusiones firmes sobre las relaciones causales.

Referencias

1. Bushman, B. J., & Huesmann, L. R. (2001). Efectos de la violencia televisada sobre la agresión. En D. Singer & J. Singer (Eds.), Manual de niños y medios de comunicación (pp. 223—254). Thousand Oaks, CA: Salvia.
2. Messerli, F. H. (2012). Consumo de chocolate, función cognitiva y premios Nobel. New England Journal of Medicine, 367, 1562-1564.