2.2.2: Gráficas de polinomios usando ceros

Gráficas de polinomios usando ceros

¿Cómo se relaciona encontrar y usar los ceros de un polinomio de grado superior con el mismo proceso que has usado en el pasado en funciones cuadráticas?

---

Graficar polinomios usando ceros

Se puede seguir el siguiente procedimiento al graficar una función polinómica.

• Utilice la prueba de plazo inicial para determinar el comportamiento final de la gráfica.
• Encuentra la (s) intercepción (s) x− de f (x) estableciendo f (x) =0 y luego resolviendo para x.
• Encuentra la intersección y−de f (x) estableciendo y=f (0) y encontrando y.
• Utilice la (s) x−intercept (s) para dividir el eje x en intervalos y luego elija puntos de prueba para determinar el signo de f (x) en cada intervalo.
• Trazar los puntos de prueba.
• Si es necesario, encuentra puntos adicionales para determinar la forma general de la gráfica.

La prueba Leading-Term

Si un _n x ⁿ es el término principal de un polinomio. Entonces el comportamiento de la gráfica como x→∞ o x→−∞ puede ser conocido por uno de los cuatro comportamientos siguientes:

2. Si un _n <0 y n par:

3. Si un _n >0 y n impar:

4. Si un _n <0 y n impar: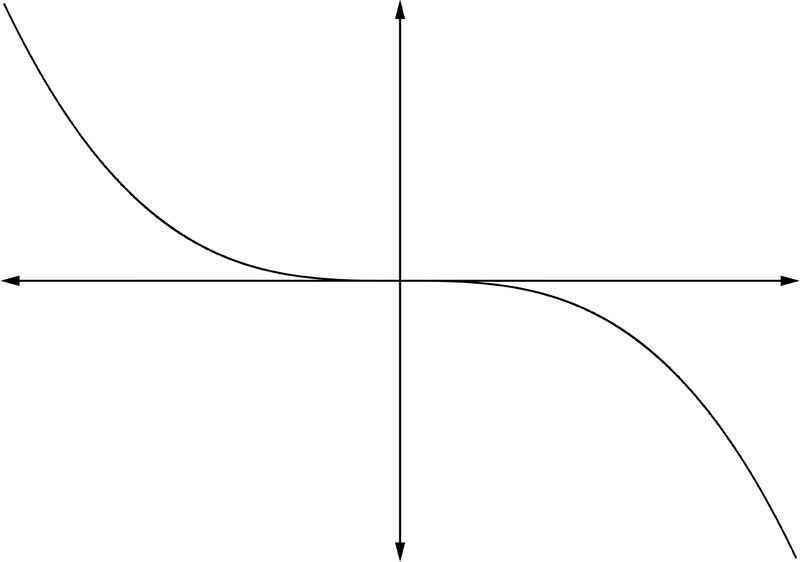

---

Ejemplos

Ejemplo 1

Anteriormente, se le pidió que identificara algunas similitudes en la gráfica usando ceros entre funciones cuadráticas y polinomios de grado superior.

Solución

A pesar de la naturaleza más compleja de las gráficas de polinomios de grado superior, el proceso general de graficar usando ceros es en realidad muy similar. En ambos casos, tu objetivo es ubicar los puntos donde la gráfica cruza el eje x o y. En ambos casos, esto se hace estableciendo el valor y igual a cero y resolviendo para x para encontrar las intercepciones del eje x, y estableciendo el valor x igual a cero y resolviendo para y para encontrar las intercepciones del eje y.

Ejemplo 2

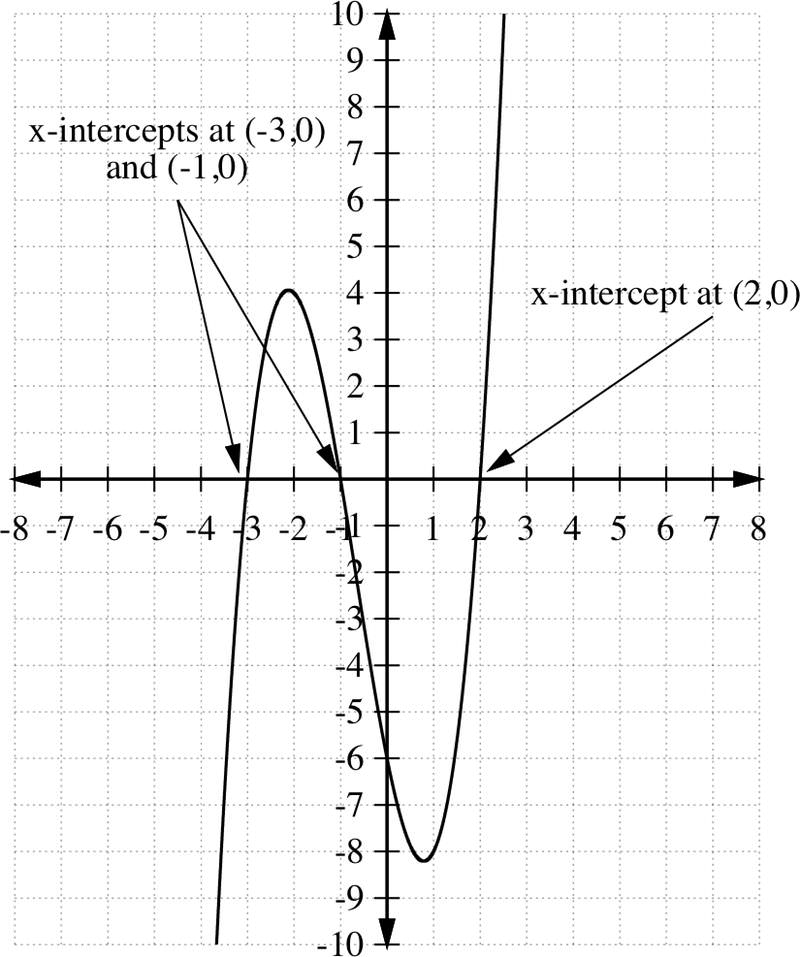
Encuentra las raíces (ceros) del polinomio:

h (x) =x ³ +2x ² −5x−6

Solución

Comience por factorización:

h (x) =x ³ +2x ² −5x−6 =( x+1) (x−2) (x+3)

Para encontrar los ceros, establezca h (x) =0 y resuelva para x.

(x+1) (x−2) (x+3) =0

Esto da

x+1=0

x−2=0

x+3=0

o

x=-1

x=2

x=-3

Entonces decimos que el conjunto de soluciones es {−3, −1,2}. Son los ceros de la función h (x). Los ceros de h (x) son los x−intercepts de la gráfica y=h (x) a continuación.

Ejemplo 3

Encuentra los ceros de g (x) =− (x−2) (x−2) (x+1) (x+5) (x+5) (x+5) (x+5).

Solución

El polinomio puede escribirse como

g (x) =− (x−2) ² (x+1) (x+5) ³

Para resolver la ecuación, simplemente la establecemos igual a cero

− (x−2) ² (x+1) (x+5) ³ =0

esto da

x−2=0

x+1=0

x+5=0

o

x=2

x=-1

x=-5

Observe la ocurrencia de los ceros en la función. El factor (x−2) ocurrió dos veces (porque estaba cuadrado), el factor (x+1) ocurrió una vez y el factor (x+5) ocurrió tres veces. Decimos que el cero que obtenemos del factor (x−2) tiene una multiplicidad k=2 y el factor (x+5) tiene una multiplicidad k=3.

Ejemplo 4

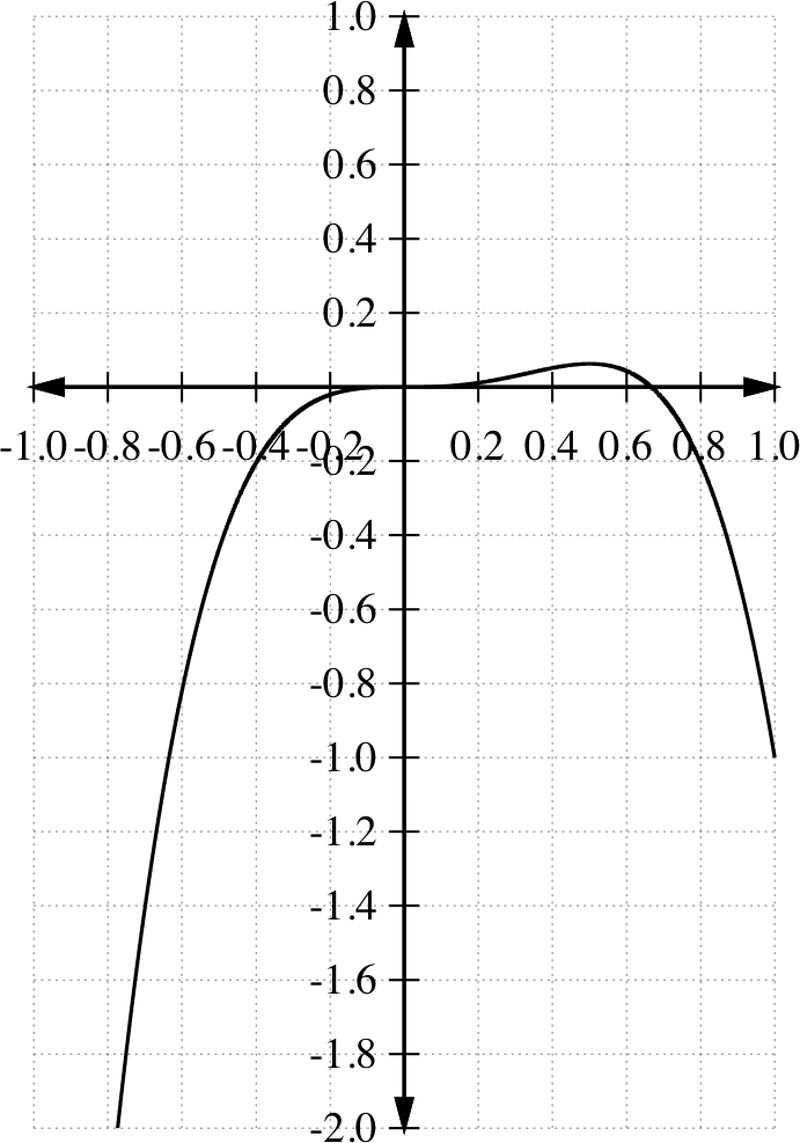
Grafica la función polinómica f (x) =−3x ⁴ +2x ³.

Solución

Dado que el término principal aquí es −3x ⁴ entonces un _n =−3<0, y n=4 par. Así, el comportamiento final de la gráfica como x→∞ y x→−∞ es el del Cuadro #2, ítem 2.

Podemos encontrar los ceros de la función simplemente estableciendo f (x) =0 y luego resolviendo para x.

−3x ⁴ +2x ³ =0

−x ³ (3x−2) =0

Esto da

x=0 o x=\(\ 2\over 3\)

Entonces tenemos dos x−intercepts, en x=0 y en x=\(\ 2\over 3\), con multiplicidad k=3 para x=0 y multiplicidad k=1 para x=\(\ 2\over 3\)

Para encontrar la intersección y−, encontramos f (0), que da

f (0) =0

Entonces la gráfica pasa el eje y en y=0.

Dado que las intercepciones x son 0 y\(\ 2\over 3\), dividen el eje x en tres intervalos: (−∞, 0), (0,\(\ 2\over 3\)) y (\(\ 2\over 3\), ∞). Ahora nos interesa determinar en qué intervalos la función f (x) es negativa y en qué intervalos es positiva. Para ello, construimos una tabla y elegimos un valor de prueba para x de cada intervalo y encontramos el f (x) correspondiente en ese valor.

Intervalo	Valor de prueba x	f (x)	Signo de f (x)	Ubicación de los puntos en la gráfica
(−∞, 0)	-1	-5	-	debajo del eje x
(0,\(\ 2\over 3\))	\(\ 1\over 2\)	\(\ 1\over 16\)	+	por encima del eje x
(\(\ 2\over 3\), ∞)	1	-1	-	debajo del eje x

Esos puntos de prueba nos dan tres puntos adicionales para trazar: (−1, −5)\(\ 1\over 2\), (,\(\ 1\over 16\)) y (1, -1). Ahora estamos listos para trazar nuestra gráfica. Tenemos un total de tres puntos de intercepción, además de los tres puntos de prueba. También sabemos cómo se está comportando la gráfica como x→−∞ y x→+∞. Esta información suele ser suficiente para hacer un boceto aproximado de la gráfica. Si necesitamos puntos adicionales, simplemente podemos seleccionar más puntos para completar la gráfica.

Ejemplo 5

Encuentra los ceros y dibuja una gráfica del polinomio

f (x) =x ⁴ −x ² −56

Solución

Esta es una ecuación factorizable,

f (x) =x ⁴ −x ² −56

= (x ² −8) (x ² +7)

Ajuste f (x) =0,

(x ² −8) (x ² +7) =0

el primer término da

x ² −8=0

x ² =0

x= ±\(\ \sqrt{8}\)

= ±\(\ 2\sqrt{2}\)

y el segundo término da

x ² +7=0

x ² =−7

x=±\(\ \sqrt{-7}\)

=±\(\ i\sqrt{7}\)

Entonces las soluciones son ±\(\ 2\sqrt{2}\) y ±\(\ i\sqrt{7}\), un total de cuatro ceros de f (x). Tenga en cuenta que sólo los ceros reales de una función corresponden a la intersección x−de su gráfica.

Ejemplo 6

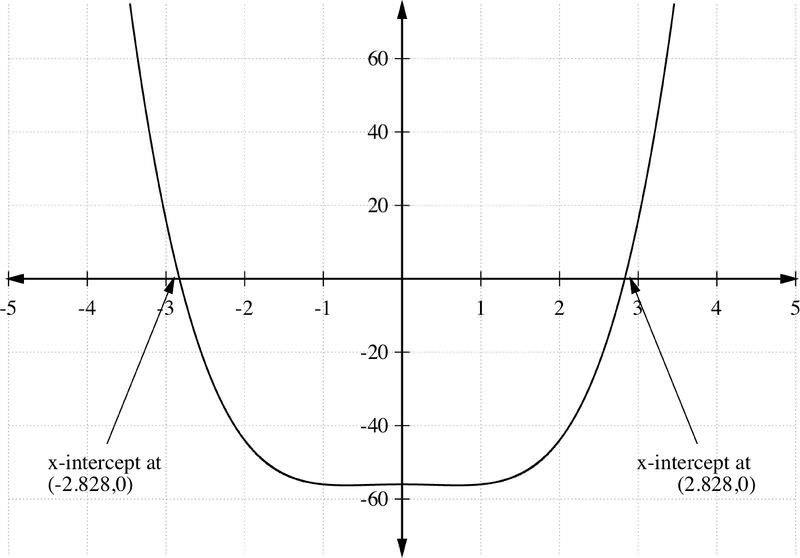
Gráfica g (x) =− (x−2) ² (x+1) (x+5) ³.

Solución

Usa los ceros para crear una tabla de intervalos y ver si la función está por encima o por debajo del eje x en cada intervalo:

Intervalo	Valor de prueba x	g (x)	Signo de g (x)	Ubicación de la gráfica en relación con el eje x
(−∞, −5)	-6	320	+	Arriba
x=−5	-5	0	NA
(-5, -1)	-2	144	+	Arriba
x=−1	-1	0	NA
(-1, 2)	0	-100	-	Abajo
x=2	2	0	NA
(2, ∞)	3	-256	-	Abajo

Por último, utilice esta información y los puntos de prueba para esbozar una gráfica de g (x).

---

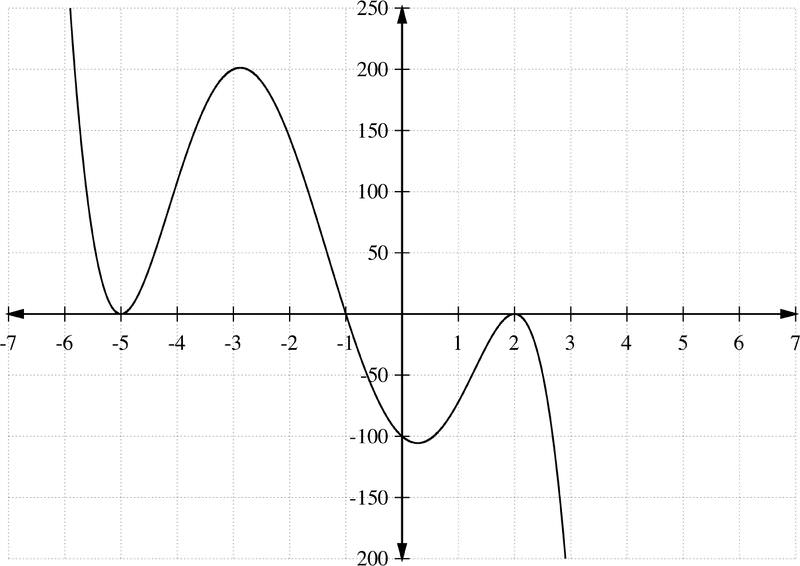
Revisar

1. Si c es un cero de f, entonces c es a/an _________________________ de la gráfica de f.
2. Si c es un cero de f, entonces (x - c) es un factor de ___________________?
3. Encuentra los ceros del polinomio: P (x) =x ³ −5x ² +6x

Considere la función: f (x) =−3 (x−3) ⁴ (5x−2) (2x−1) ³ (4−x) ².

4. ¿Cuántos ceros (intercepciones x) hay?
5. ¿Cuál es el término líder?

Encuentra los ceros y grafica el polinomio. Asegúrese de etiquetar las intercepciones x, y -interceptar (si es posible) y tener un comportamiento final correcto. Puede utilizar la tecnología para las preguntas 9-12.

6. P (x) =−2 (x+1) ² (x−3)
7. P (x) =x ³ +3x ² −4x−12
8. f (x) =−2x ³ +6x ² +9x+6
9. f (x) =−4x ² −7x+3
10. f (x) =2x ⁵ +4x ³ +8x ² +6x
11. f (x) =x ⁴ −3x ²
12. g (x) =x ² −|x|
13. Dado: P (x) = (3x+2) (x−7) ² (9x+2) ³

Estado:

1. El término principal:
2. El grado del polinomio:
3. El coeficiente principal:

Determinar la ecuación del polinomio con base en la gráfica:

14. 

15. 

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.4.

---

El vocabulario

Término	Definición
Función cúbica	Una función cúbica es una función que contiene un término x ^3 como la potencia más alta de x.
Interceptar	Las intercepciones de una curva son las ubicaciones donde la curva interseca los ejes x e y. Una intersección x es un punto en el que la curva cruza el eje x. Una intersección y es un punto en el que la curva cruza el eje y.
intervalo	Un intervalo es una parte específica y limitada de una función.
Prueba Leading-Term	La prueba de término inicial es una prueba para determinar el comportamiento final de una función polinómica.
Polinomio	Un polinomio es una expresión con al menos un término algebraico, pero que no indica división por una variable ni contiene variables con exponentes fraccionarios.
Gráfica polinomial	Una gráfica polinómica es la gráfica de una función polinómica. El término se usa más comúnmente para funciones polinómicas con un grado de al menos tres.
Función Quártica	Una función cuártica es una función f (x) que contiene un término x ^4 como la potencia más alta de “x”.
Raíces	Las raíces de una función son los valores de x que hacen y igual a cero.
Ceros	Los ceros de una función f (x) son los valores de x que hacen que f (x) sea igual a cero.