2.5.1: Desigualdades cuadráticas

Desigualdades cuadráticas

¿Cómo expresarías lo siguiente como una función?

Se supone que debes cortar tu césped cuadrado para tus padres, pero el cortacésped solo tiene parte de un tanque de gasolina. Si puedes cortar 2500 sf por galón, y la segadora tiene aproximadamente 2.5 galones en ella, ¿cuál es la longitud máxima de un lado del césped que puedes cortar? Si tu césped mide 75 pies de largo, ¿necesitarás más gasolina?

---

Desigualdades cuadráticas

Las desigualdades cuadráticas son desigualdades que tienen una de las siguientes formas

hacha ² +bx+c>0

y

hacha ² +bx+c<0

Podemos resolver estas desigualdades utilizando las técnicas que hemos aprendido sobre la resolución de ecuaciones cuadráticas. Por ejemplo, considere la gráfica de la ecuación:

y=f (x) =x ² +x−6

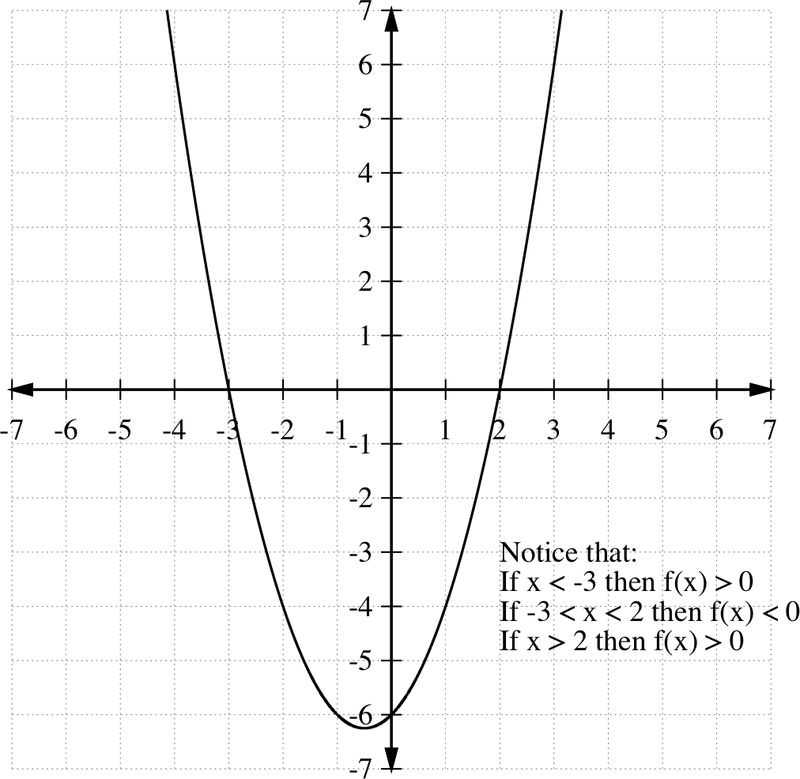[Figura1]

Observe que la curva cruza el eje x en -3 y 2. De la gráfica, notamos lo siguiente

• Si x<−3 entonces f (x) >0
• Si −3<x<2, entonces f (x) <0
• Si x>2, entonces f (x) >0

Por lo tanto, x ² +x−6>0 siempre que x<−3 o x>2, y x ² +x−6<0 cuando −3<x<2.

---

Ejemplos

Ejemplo 1

Antes, se le dio una pregunta sobre cortar un césped.

Si puedes cortar 2500 sf de pasto por galón de gas, y la segadora tiene 2.5 galones en ella, ¿cuál es la longitud máxima de un lado del césped que puedes cortar?

Si su césped mide 75 pies de largo, ¿necesitará más gasolina?

Solución

Sabemos que la función S ² <6250 describe las posibles longitudes laterales de formas cuadradas que podrías segar antes de quedarte sin gas (si tienes problemas para entender por qué, consulta el Ejemplo 4 para un proceso similar).

Resolver para S da:

\ (\\ begin {array} {l}
\ sqrt {s^ {2}} =\ sqrt {6250}\\
s=79
\ end {array}\)

Con 2.5 galones de gas, podrías cortar un cuadrado de hasta aproximadamente 79 pies en cada lado.

No debería necesitar más gas si el césped mide solo 75 pies de largo en cada lado.

Ejemplo 2

¿Cuál es el conjunto de soluciones de la desigualdad 2x ² +7x−4<0?

Solución

Lo mejor es graficar la función f (x) =2x ² +7x−4 y buscar los valores de x de tal manera que la desigualdad f (x) <0 sea verdadera.

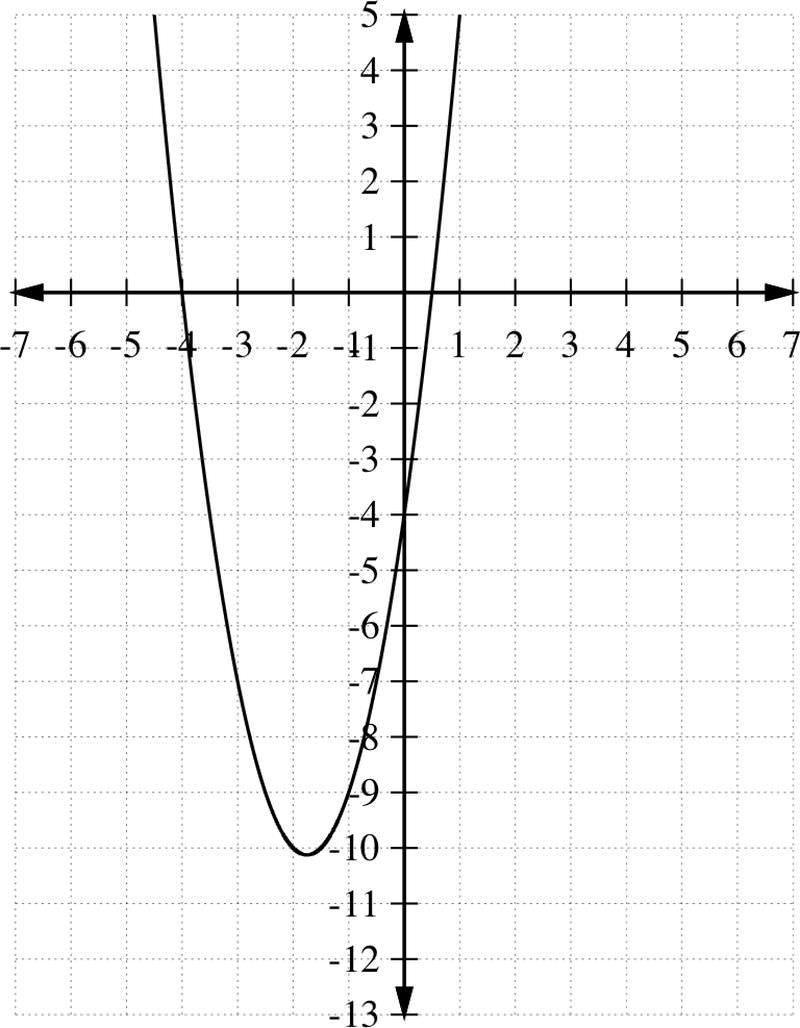
Así, a partir de la gráfica, 2x ² +7x−4<0 solo si

\(\ -4<x<\frac{1}{2}\)

Entonces el conjunto de soluciones es\(\ x \in\left(-4, \frac{1}{2}\right)\) o en notación de constructor de conjuntos,\(\ \left\{x \mid-4<x<\frac{1}{2}\right\}\)

Aunque el método de graficar para encontrar el conjunto de soluciones de una desigualdad es fácil de seguir, se puede utilizar otro método algebraico. El método algebraico implica encontrar las intercepciones x de la gráfica y luego dividir el eje x en intervalos separados por las intercepciones x. Los siguientes ejemplos ilustran el método.

Ejemplo 3

Encuentre el conjunto de soluciones de la desigualdad cuadrática x ² +2x−8>0 sin graficar.

Solución

Para encontrar el conjunto de soluciones sin graficar, primer factor:

x ² +2x−8=0

(x+4) (x−2) =0

Recordando la regla del producto cero, podemos ver que las dos soluciones a esta ecuación cuadrática son x=−4 y x=2, así, las x−intercepciones de la función f (x) =x ² +2x−8 son -4 y 2.

Estos puntos dividen el eje x en tres intervalos: (−∞, −4) | (−4,2) | (2, ∞). Podemos elegir un punto de prueba de cada intervalo, sustituirlo por f (x) y ver si la función es negativa o positiva con ese valor como x. Este procedimiento se puede simplificar haciendo una tabla como se muestra a continuación:

Intervalo	Punto de prueba	¿Es x ^2 +2x−8 positivo o negativo?	¿Parte del conjunto de soluciones?
(−∞, −4)	−5	+	si
(−4,2)	1	−	no
(2, +∞)	3	+	si

De la tabla, concluimos que desde x ² +2x−8>0 si y solo si x<−4 y x>2. El conjunto de soluciones también se puede escribir como:

x∈ (−∞, −4) (2, +∞)

Algunos problemas en la ciencia involucran desigualdades cuadráticas. El siguiente ejemplo ilustra una de esas aplicaciones.

Ejemplo 4

Un rectángulo tiene una longitud de 10 metros más del doble de ancho. Encuentra todas las anchuras posibles que resulten en que el área del rectángulo no supere los 100 metros cuadrados.

Solución

Sea w el ancho del rectángulo y l su longitud. Dada la información en la pregunta, podemos decir:

l=10+2w

Entonces podemos usar la fórmula para el área de un rectángulo:

área=l×w

Sustituir 10+2w por l da:

área=w× (10+2w)

El área no puede superar los 100 m ², por lo que

10w+2w ² <100

o

2w ² +10w−100<0

Simplifique dividiendo ambos lados por 2:

w ² +5w−50<0

Factorial el trinomio:

w ² +5w−50 =( w+10) (w−5)

Entonces los puntos de partición son 5 y -10, lo que significa que tenemos tres intervalos. Dado que el ancho no puede ser negativo, podemos ignorar con seguridad -10. Eso significa que el área máxima es de 100 m ²

w<5.

El ancho debe ser inferior a 5 metros.

Ejemplo 5

Encuentra el conjunto de soluciones de la desigualdad x ² ≤16.

Solución

Establezca la función igual a cero:

x ² −16=0

Factor para encontrar los valores críticos (puntos donde la gráfica cruza el eje x, cambiando así los signos):

(x−4) (x+4) =0

Por la regla de producto cero: x=4 o x=−4

Eso nos da tres secciones en la gráfica:

x≤−4

−4≤x≤4

4≤x

Pruebe un valor de muestra de cada división para identificar posibles conjuntos de soluciones.

Set	x≤−4	−4≤x≤4	4≤x
Valor de prueba	−5		5
f (x) verdadero con valor?	4⋅ (−5) ^2 =10016 No	40 ^2 =0≤16 Sí	45 ^2 =10016 No

Por lo tanto, el conjunto de soluciones es −4≤x≤4.

Ejemplo 6

Grafique el conjunto de soluciones: (x−3) (x+4) ≥0.

Solución

Las soluciones a (x−3) (x+4) ≥0 se pueden identificar con las reglas para multiplicar números negativos:

Recordemos de Pre-Álgebra que un número par de negativos produce una respuesta positiva, y un número impar de negativos produce una respuesta negativa.

Desde (x−3) (x+4) ≥0 sabemos que necesitamos una respuesta positiva o cero.

Por tanto, ya sea:

Caso #1: (x−3) ≥0→x≥3 y (x+4) ≥0→x≥−4

o

Caso #2: (x−3) ≤0→x≤3 y (x+4) ≤0→x≤−4

Dado que cualquier número mayor a 3 ya es mayor que -4, del Caso #1 obtenemos: x≥3

Como cualquier número menor que -4 ya es menor que 3, del Caso #2 obtenemos x≤−4

Por lo tanto, nuestra respuesta es x≤−4 o x≥3

En notación de conjunto: x∈ (−∞, −4] [3, +∞)

Para graficar esta información, dibujamos una gráfica de líneas, y marcamos los valores que puede ser x, con puntos sólidos en los números finales para indicar que esos valores están incluidos.

Visualmente es decir:

“frameborder="0" height="450px” name="99198" src=” https://www.ck12.org/flx/show/video/...ties-Example-2 "thumbnailurl="” title="VideoObject? hash=f688e36d565e0820730d1d47d13380a6" uploaddate="2016-07-06 16:34:48 "width=” 95% “>

---

Revisar

Grafique los conjuntos de soluciones a continuación en una recta numérica:

1. x<3 o x>4
2. x≥−5 y x≥3
3. x<6 y x≥−2
4. x>7 o x≥−4
5. x≤−8 y x>3

Identificar puntos críticos, resolver y graficar:

6. x ² +9x>−14
7. x ² −5x≤50
8. x ² +2x≤48
9. \(\ x-\frac{20}{x}-8<0\)(pista: multiplicar ambos lados por x primero)
10. \(\ x+10 \geq-\frac{21}{x}\)
11. (x+6) (x−3) >0
12. (x−8) (x+1) >0
13. x ² −x≥90
14. 3x ² −23x≤8
15. x ² +x−6>0

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.9.

---

El vocabulario

Término	Definición
Valores Críticos	Los valores críticos son las intercepciones x−de una función cuadrática.
intervalo	Un intervalo es una parte específica y limitada de una función.
desigualdad cuadrática	Una desigualdad cuadrática es una expresión cuadrática que se especifica para ser mayor o menor que un valor dado.
Raíces	Las raíces de una función son los valores de x que hacen y igual a cero.
Regla de producto cero	La regla de producto cero establece que si el producto de dos expresiones es igual a cero, entonces al menos una de las expresiones originales mucho será igual a cero.

---

Atribuciones de imagen

1. [Figura 1]
   Crédito: Fundación CK-12; Desmos
   Fuente: Desmos