5.2.1: Productos Dot
- Page ID
- 108956
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Producto de punto y ángulo entre dos vectores
Si bien dos vectores no se pueden multiplicar estrictamente como los números pueden, hay dos formas diferentes de encontrar el producto entre dos vectores. El producto cruzado entre dos vectores da como resultado un nuevo vector perpendicular a los otros dos vectores. Puedes estudiar más sobre el producto cruzado entre dos vectores cuando tomas Álgebra Lineal. El segundo tipo de producto es el producto punto entre dos vectores lo que da como resultado un número regular. Otros nombres para el producto punto incluyen producto interno y producto escalar. Este número representa cuánto de un vector va en dirección al otro. En un sentido, indica cuánto coinciden los dos vectores entre sí. Este concepto se centrará en el producto punto entre dos vectores.
¿Cuál es el producto punto entre <−1,1> y <4,4>? ¿Qué significa el resultado?
Propiedades del Producto Dot
El producto punto se define como:\(\ u \cdot v=<u_{1}, u_{2}>\cdot<v_{1}, v_{2}>=u_{1} v_{1}+u_{2} v_{2}\)
Este procedimiento establece que se multiplican los valores correspondientes y luego se suman los productos resultantes. Se puede trabajar con vectores que son más de dos dimensiones de la misma manera.
Antes de probar este procedimiento con números específicos, observe los siguientes pares de vectores y estimaciones relativas de su producto punto.
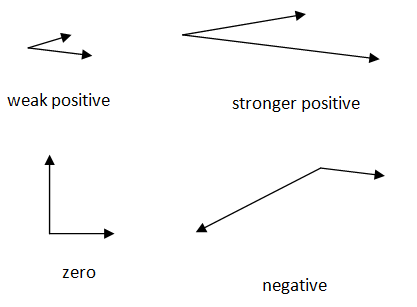
Observe cómo los vectores que van generalmente en la misma dirección tienen un producto de punto positivo. Piense en dos fuerzas que actúan sobre un solo objeto. Un producto de punto positivo implica que estas fuerzas están trabajando juntas al menos un poco. Otra forma de decir esto es que el ángulo entre los vectores es menor a 90 o.
Hay muchas propiedades importantes relacionadas con el producto dot. Los dos más importantes son 1) lo que sucede cuando un vector tiene un producto de punto consigo mismo y 2) cuál es el producto punto de dos vectores que son perpendiculares entre sí.
- \(\ v \cdot v=|v|^{2}\)
- \(\ v\)y\(\ u\) son perpendiculares si y solo si\(\ v \cdot u=0\)
La propiedad conmutativa,\(\ u \cdot v=v \cdot u\), se mantiene para el producto punto entre dos vectores. La siguiente prueba es para vectores bidimensionales aunque se mantiene para cualquier vector dimensional.
Comience con los vectores en forma de componentes.
\ (\\ begin {array} {l}
u=<u_ {1}, u_ {2} >\\
v=<v_ {1}, v_ {2} >
\ end {array}\)
Después aplique la definición de producto punto y reorganice los términos. La propiedad conmutativa ya es conocida por números regulares por lo que podemos usar eso.
\ (\\ begin {alineada}
u\ cdot v &=\ izquierda\ langle u_ {1}, u_ {2} >\ cdot<v_ {1}, v_ {2} >\ derecha. \\
&=u_ {1} v_ {1} +u_ {2} v_ {2}\\
&=v_ {1} u_ {1} +v_ {2} u_ {2}\\
&=<v_ {1}, v_ {2} >\ cdot<u_ {1}, u_ {2} >\\
&=v\ cdot u
\ end {alineado}\)
La propiedad distributiva, u⋅ (v+w) =uv+uw, también se mantiene bajo el producto punto. La siguiente prueba trabajará con vectores bidimensionales aunque la propiedad sí se mantiene en general.
\ (\\ comenzar {alineado}
u=<u_ {1}, u_ {2} >, v=<v_ {1}, v_ {2} >, w &=\ izquierda\ langle w_ {1}, w_ {2}\ derecha\ rangle\\
u\ cdot (v+w) &=u\ cdot\ cdot\ izquierda (+ <v_ {1}, v_ {2} > \<w_ {1}, w_ {2} > derecha)\\ &=u
\ cdot \<v_ {1} +w_ {1}, v_ {2} +w_ {2} >\ &=<u_
{1}, u_ {2} >\ cdot<v_ {1} +w_ {1}, v_ {2} +w_ {2} >\\
&=u_ {1}\ izquierda (v_ {1} +w_ {1}\ derecha) +u_ {2}\ izquierda (v_ {2} +w_ {2}\ derecha)\\
&=u_ {1} v_ {1} +u_ {1} w_ {1} +u_ {2} v_ {2} +u_ _ {2} w_ {2}\\
&=u_ {1} v_ {1} +u_ {2} v_ {2} +u_ {1} w_ {1} +u_ {2} w_ {2}\\
&=u\ cdot v+v\ cdot w
\ end {alineado}\)
El producto punto puede ayudarte a determinar el ángulo entre dos vectores usando la siguiente fórmula. Observe que en el numerador se requiere el producto punto porque cada término es un vector. En el denominador solo se requiere la multiplicación regular porque la magnitud de un vector es solo un número regular que indica longitud.
\(\ \cos \theta=\frac{u \cdot v}{|u||v|}\)
Vea la parte de este video enfocándose en el producto punto:
Ejemplos
Anteriormente, se le pidió que encontrara el producto punto entre los dos vectores <−1,1> y <4,4>.
Solución
Se puede computar como:
(−1) (4) +1 (4) =−4+4=0
El resultado de cero tiene sentido porque estos dos vectores son perpendiculares entre sí.
Encuentra el producto punto entre los siguientes vectores: <3,1>⋅<5, −4>
Solución
\(\ u\)=<3,5>
Demostrar el ángulo entre dos vectores fórmula:
\(\ \cos \theta=\frac{u \cdot v}{|u||v|}\)
Solución
Empezar con la ley de los cosenos.
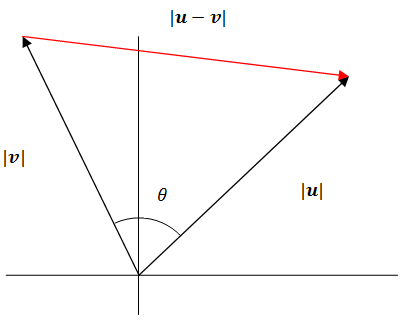
\ (\\ begin {alineado}
|u-v|^ {2} &=|v|^ {2} +|u|^ {2} -2|v||u|\ cos\ theta\
(u-v)\ cdot (u-v) &=\\
u\ cdot u-2 u\ cdot v+v\ cdot v &=\\
|u|^ {2} -2 u\ punto v+|v|^ {2} &=\\
-2 u\ cdot v &=-2|v||u|\ cos\ theta\
\ frac {u\ cdot v} {|u||v|} &=\ cos\ theta
\ fin {alineado}\)
Encuentra el producto punto entre los siguientes vectores.
\(\ (4 i-2 j) \cdot(3 i-8 j)\)
Solución
Los vectores unitarios estándar se pueden escribir como vectores componentes.
\(\ <4,-2>\cdot<3,-8>=12+(-2)(-8)=12+16=28\)
¿Cuál es el ángulo entre\(\ u=<3,5>\) y\(\ v=<2,8>\)?
Solución
Utilice la fórmula del ángulo entre dos vectores.
\(\ u=<3,5>\text { and } v=<2,8>\)
\ (\\ begin {alineado}
\ frac {u\ cdot v} {|u||v|} &=\ cos\ theta\
\ frac {<3,5>\ cdot<2,8>} {\ sqrt {34}\ cdot\ sqrt {68}} &=\ cos\ theta\
\ frac {6+40} {\ sqrt {34}\ cdot\ sqrt {68}} &=\ cos\ theta\
\ cos ^ {-1}\ izquierda (\ frac {46} {\ sqrt {34}\ cdot\ sqrt {68} }\ derecha) &=\ theta\\
16.93^ {\ circ} &\ approx\ theta
\ final {alineado}\)
Revisar
Encuentra el producto punto para cada uno de los siguientes pares de vectores.
- <2,6><−3,5>
- <5, −1><4,4>
- <−3, −4><2,2>
- <3,1><6,3>
- <−1,4><2,9>
Encuentra el ángulo entre cada par de vectores a continuación.
- <2,6><−3,5>
- <5, −1><4,4>
- <−3, −4><2,2>
- <3,1><6,3>
- <−1,4><2,9>
- ¿Qué es\(\ v \cdot v\)?
- ¿Cómo se puede utilizar el producto punto para encontrar la magnitud de un vector?
- ¿Qué es\(\ 0 \cdot v\)?
- Demostrar que\(\ (c u) \cdot v=u \cdot(c v)\) donde\(\ c\) es una constante.
- Mostrar que <2,3> es perpendicular a <1.5, −1>.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.4.

