5.2.2: Proyecciones Escalares

Proyecciones escalares

Como ingeniero, o piloto, o piloto de autos de carreras, o incluso chef, a menudo puede ser útil determinar el resultado de diferentes cantidades y direcciones de fuerza aplicadas a una acción en particular para decidir sobre el mejor uso de la fuerza, altitud, velocidad o calor agregados para lograr el resultado óptimo.

Esta lección trata sobre proyecciones escalares, que permiten hacer las cosas anteriores y todo un sinfín de otras.

---

Proyecciones escalares

Una proyección escalar permite investigar el resultado de diferentes “longitudes” de un vector en un estudio general. La proyección de un vector en una dirección particular es, en efecto, el resultado de aplicar un valor específico en esa dirección. Recordemos que el producto de punto de un vector es una cantidad escalar que describe solo la magnitud de un vector en particular. Una proyección escalar viene dada por el producto de punto de un vector con un vector unitario para esa dirección.

Por ejemplo, las notaciones de componentes para los vectores que se muestran a continuación son AB=±4,3⟩ y D=2+3, −1.25⟩.

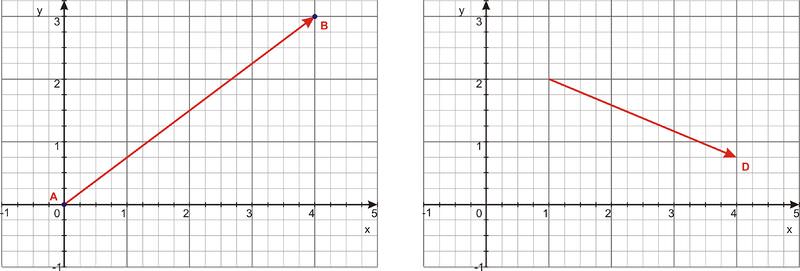
La proyección escalar del vector AB sobre\(\ \hat{x}\) está dada por

\(\ \overrightarrow{A B} \times \hat{x}=(4 \cdot 1)+(3 \cdot 0)+(0 \cdot 0)=4\)

La proyección escalar del vector AB sobre\(\ \hat{y}\) está dada por

\(\ \overrightarrow{A B} \times \hat{y}=(4 \cdot 0)+(3 \cdot 1)+(0 \cdot 0)=3\)

Y la proyección escalar del vector AB sobre\(\ \hat{z}\) está dada por

\(\ \overrightarrow{A B} \times \hat{z}=(4 \cdot 0)+(3 \cdot 0)+(0 \cdot 1)=0\)

Las proyecciones escalares de AB en las direcciones x e y son números distintos de cero porque el vector se encuentra en el plano x-y. La proyección escalar de AB en la dirección z es igual a cero, porque la dirección z es perpendicular a AB.

Proyecciones vectoriales

La proyección vectorial de un vector en una dirección dada tiene una magnitud igual a la proyección escalar. La dirección de la proyección vectorial es la misma que la del vector unitario de esa dirección dada. Recordemos que cuando un vector\(\ \vec{v}\) se multiplica por un escalar s, sus componentes están dados por

\(\ \overrightarrow{s v}=\left\langle s v_{x}, s v_{y}, s v_{z}\right\rangle\)

Para calcular la proyección vectorial de AB en la dirección del vector D, utilice la proyección escalar calculada en el ejemplo anterior y el vector unitario\(\ \vec{D}\).

\(\ (\overrightarrow{A B} \times \vec{D}) \vec{D}=\langle(1.23 \cdot 0.923),(1.23 \cdot-0.385)\rangle=\langle 1.135,-0.474\rangle\)

---

Ejemplos

Ejemplo 1

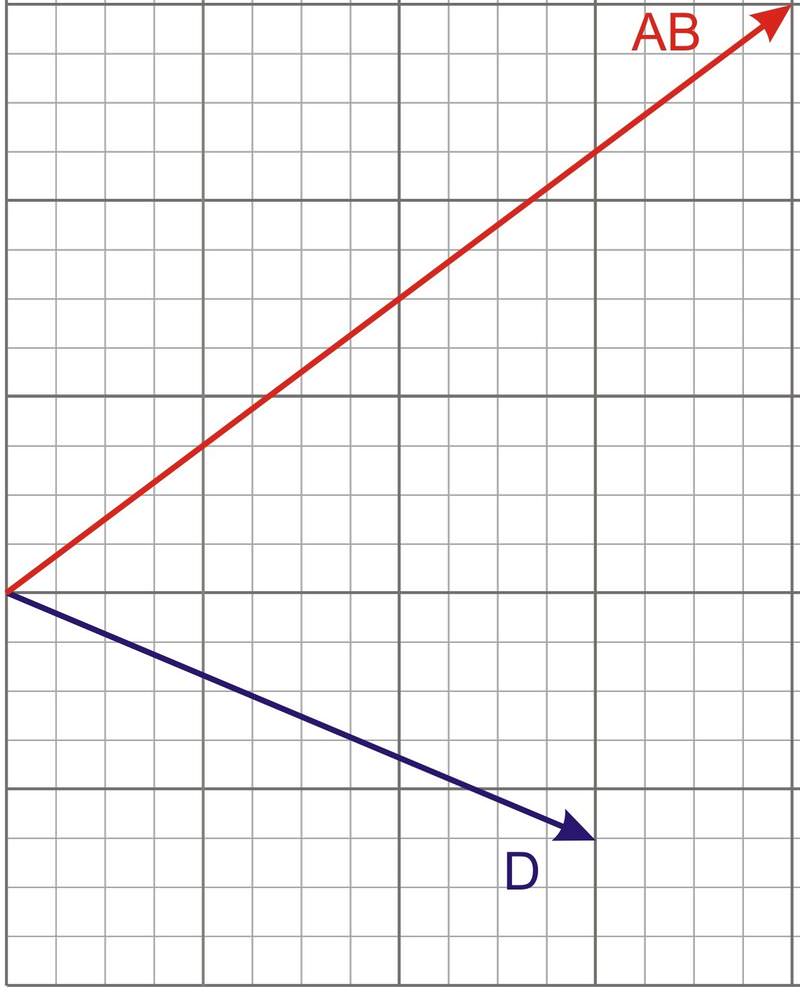
El siguiente diagrama muestra ambos vectores AB y D juntos en la misma cuadrícula. Determinar la proyección escalar del vector AB en la dirección del vector D.

Solución

Para encontrar la proyección escalar en la dirección de otro vector necesitamos conocer el vector unitario en la dirección del vector D.

Primero, los componentes de\(\ \vec{D}\) son

\(\ \vec{D}=\langle 3,-1.25\rangle\)

Ahora la magnitud de\(\ \vec{D}\) es

\(\ |D|=\sqrt{\left(D_{x}\right)^{2}+\left(D_{y}\right)^{2}}=\sqrt{3^{2}+(-1.25)^{2}}=\sqrt{9+1.5625}=\sqrt{10.5625}=3.25\)

Finalmente, el vector de dirección de\(\ \vec{D}\) es

\ (\\ begin {array} {l}
\ vec {D} =\ frac {\ vec {D}} {|D|} =\ frac {3\ sombrero {x} + (-1.25)\ sombrero {y}} {3.25} =\ frac {3} {3.25}\ sombrero {x} +\ frac {-1.25} {3.25}\ sombrero {y}\\
\ vec {D} =\ langle 0.923, -0.385\ rangle
\ end {array}\)

Ahora podemos usar el punto-producto para calcular la proyección escalar de AB en la dirección del vector D.

\(\ \overrightarrow{A B} \times \vec{D}=(3 \cdot 0.923)+(4 \cdot-0.385)+(0 \cdot 0)=2.769+(-1.54)=1.23\)

Ejemplo 2

Determinar la proyección escalar del vector\(\ \vec{R}=\langle 27,39,52\rangle\) en la dirección de\(\ \vec{T}=\langle 44,26,17\rangle\).

Solución

La proyección escalar de un vector en la dirección del otro es el producto de punto del primer vector con el vector unitario representando la dirección del segundo vector. Para calcular la proyección escalar, necesitamos determinar el vector unitario en la dirección del vector\(\ \vec{T}=\langle 44,26,17\rangle\). Recuerde que un vector unitario es igual a la relación del vector y su magnitud, por lo tanto primero necesitamos calcular la longitud del vector\(\ \vec{T}\)

\ (\\ begin {array} {l}
|\ vec {T} |=\ sqrt {T_ {x} ^ {2} +T_ {y} ^ {2} +T_ {z} ^ {2}} =\ sqrt {(44) ^ {2} + (26) ^ {2} + (17) ^ {2}} =\ sqrt {1936+676+289}\\
=\ sqrt {2901} =53.86\
\ vec {T} =\ frac {\ vec {T}} {|\ vec {T} |} =\ frac {\ langle 44,26,17\ rangle} {53.86} =\ izquierda\ langle\ frac {44} {53.86},\ frac {26} {53.86},\ frac {17} {53.86}\ derecha\ rangle=\ langle 0.8169,0.4827,0.3156\ rangle
\ end {array}\)

Ahora podemos calcular la proyección escalar de\(\ \vec{R}\) sobre\(\ \vec{T} \) calculando el producto punto

\ (\\ begin {array} {l}
\ vec {R}\ times\ vec {T} =( 27\ cdot 0.8169) + (39\ cdot 0.4827) + (52\ cdot 0.3156) =22.0563+18.6253
+16.4112=57.0928
\ end {array}\)

Ejemplo 3

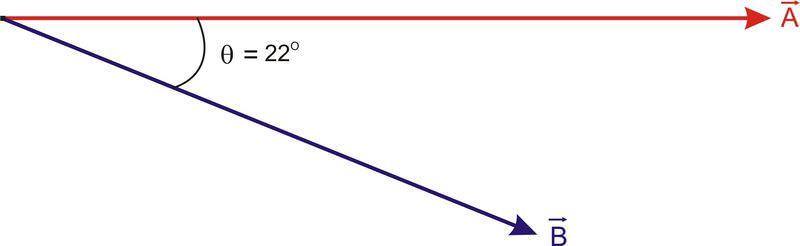
Determinar la proyección vectorial de\(\ \vec{A}\) en la dirección de\(\ \vec{B}\) y la proyección vectorial de\(\ \vec{B}\) en la dirección de\(\ \vec{A} \cdot \vec{A}=7 c m \ @\ 0^{\circ}\) y\(\ \vec{B}=4 c m\ @\ -22^{\circ}\).

Solución

La proyección vectorial de un vector en la dirección de otro vector viene dada por\(\ (\vec{A} \times \vec{B}) \vec{B}\), donde\(\ \vec{B}\) está el vector unitario en la dirección de\(\ \vec{B}\). Ya que es un vector unitario\(\ \vec{B}\) tiene una magnitud de 1 y tiene la misma dirección que\(\ \vec{B}, \vec{B}=1\ @\ -22^{\circ}\). Por lo tanto,\(\ (\vec{A} \times \vec{B}) \vec{B}=(|\vec{A} \| \vec{B}| \cos \theta) \vec{B}=((7)(1) \cos 22)\ @\ -22^{\circ}=6.49\ @\ -22^{\circ}\)

La proyección vectorial de un vector en la dirección de otro vector viene dada por\(\ (\vec{B} \times \vec{A}) \vec{A}\), donde\(\ \vec{A}\) está el vector unitario en la dirección de\(\ \vec{A}\). Ya que es un vector unitario\(\ \vec{A}\) tiene una magnitud de 1 y tiene la misma dirección que\(\ \vec{A}, \vec{A}=1\ @\ 0^{\circ}\). Por lo tanto,\(\ (\vec{B} \times \vec{A}) \vec{A}=(|\vec{B}||\vec{A}| \cos \theta) \vec{A}=((4)(1) \cos 22)\ @\ 0^{\circ}=3.71\ @\ 0^{\circ}\)

Ejemplo 4

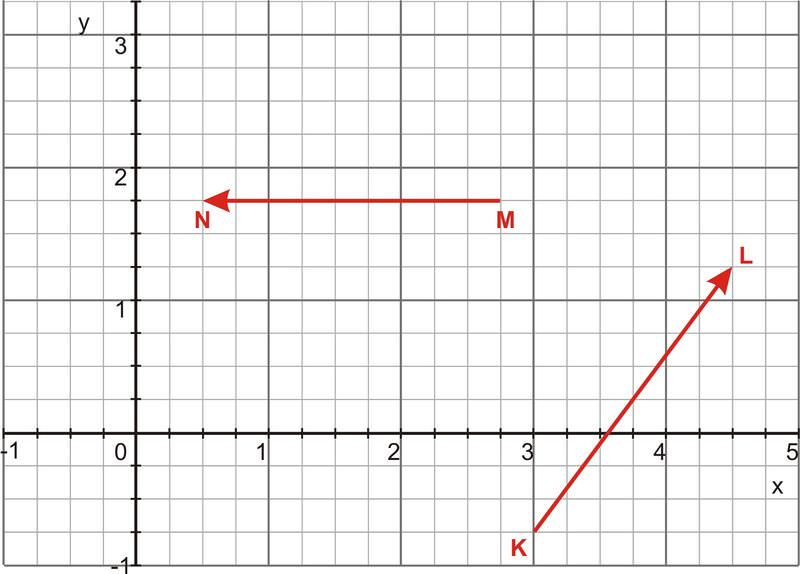
Determinar la proyección vectorial del vector\(\ \overrightarrow{M N}\) sobre el vector\(\ \overrightarrow{K L}\).

Solución

La progresión del vector de un vector a un segundo vector es la multiplicación de los productos de punto de los dos vectores y el vector unitario que define la dirección del segundo vector. En este caso,\(\ (\overrightarrow{M N} \times \overrightarrow{K L}) \overrightarrow{K L}\). Primero necesitamos identificar los componentes de los dos vectores usando la información dada en la gráfica. En este caso,\(\ \overrightarrow{M N}=\langle-2.25,0.0\rangle\) y\(\ \overrightarrow{K L}=\langle 1.5,2,0\rangle\). Entonces necesitamos determinar el producto punto de los dos vectores.

\ (\\ comenzar {matriz} {l}
\ overrightarrow {M N}\ veces\ overrightarrow {K L} =( M N) _ {x} (K L) _ {x} + (M N) _ {y} (K L) _ {y} + (M N) _ {z} (K L) _ {z}\\
=( 2.25) (1.5) + (2) (0) + (0) (0) =3.375
\ end {array}\)

También necesitamos determinar el vector unitario en la dirección de\(\ \overrightarrow{K L}\). Recuerde que un vector unitario es igual a la relación del vector y su magnitud, por lo tanto primero necesitamos calcular la longitud del vector\(\ \overrightarrow{K L}\).

\ (\\ begin {array} {l}
|\ overrightarrow {K L} |=\ sqrt {(K L) _ {x} ^ {2} + (K L) _ {y} ^ {2} + (K L) _ {z} ^ {2}} =\ sqrt {(1.5) ^ {2} + (2) ^ {2} + (0) ^ {2}} =\ sqrt {2.25+4+0}\\
=\ sqrt {6.25} =2.5\
\ overrightarrow {K L} =\ frac {\ overrightarrow {K L}} {|\ overrightarrow {K L} |} =\ frac {\ langle 1.5,2.0,0\ rangle} {2.5} =\ izquierda\ langle\ frac {1.5} {2.5},\ frac {2} {2.5},\ frac {0} {2.5}\ derecha\ rangle=\ langle 0.6,0.8,0\ rangle
\ end {array}\)

Por último, multiplicamos el producto de punto de los dos vectores por este vector unitario,

\(\ (\overrightarrow{M N} \times \overrightarrow{K L}) \overrightarrow{K L}=(3.375)\langle 0.6,0.8,0\rangle=\langle 2.025,2.7,0\rangle\)

---

Revisar

1. Calcular el resultado de un múltiplo escalar de 6 en el vector\(\ \langle 1,19\rangle\)
2. Calcular el resultado de un múltiplo escalar de (-8) en el vector\(\ \langle 7,8\rangle\)
3. Calcular el resultado de un múltiplo escalar de 15 en el vector\(\ \langle-7,3\rangle\)
4. Calcular el resultado de un múltiplo escalar de (-11) en el vector\(\ \langle-9,20\rangle\)
5. Calcular el resultado de un múltiplo escalar de 16 en el vector\(\ \langle 9,10\rangle\)
6. Dado Vector\(\ A=\langle-4,6\rangle\) y Vector\(\ B=\langle 9,15\rangle\). ¿Cuál es la proyección de A sobre B?
7. ¿Cuál es la proyección de\(\ \langle 2,10\rangle\) onto\(\ \langle 1,3\rangle\)?
8. Dado Vector\(\ C=\langle 1,2\rangle\) y Vector\(\ D=\langle 1,11\rangle\). ¿Cuál es la proyección de C sobre D?
9. Dado Vector\(\ E=\langle-5,3\rangle\) y Vector\(\ F=\langle-1,18\rangle\). ¿Cuál es la proyección de E sobre F?
10. ¿Cuál es la proyección de\(\ \langle-2,1\rangle\) onto\(\ \langle-5,6\rangle\)?
11. Dado Vector\(\ \mathrm{H}=\langle 8 i+11 j\rangle\) y Vector\(\ I=\langle-2 i+15 j\rangle\) ¿Cuál es la proyección de H sobre I?
12. ¿Cuál es la proyección de\(\ \langle-1,6\rangle\) onto\(\ \langle 8,16\rangle\)?
13. ¿Cuál es la proyección de\(\ \langle-1,8\rangle\) onto\(\ \langle 7,8\rangle\)?
14. Dado Vector\(\ \mathrm{J}=\langle-4 i+8 j\rangle\) y Vector\(\ K=\langle-8 i+10 j\rangle\). ¿Cuál es la proyección de J sobre K?
15. Dado Vector\(\ L=\langle-4,3\rangle\) y Vector\(\ M=\langle 7,17\rangle\). ¿Cuál es la proyección de L sobre M?

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.5.

---

vocabulario

Término	Definición
producto punto	El producto punto también se conoce como producto interno o producto escalar. Las dos formas del producto punto son\(\ \vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta \text { and } \vec{a} \cdot \vec{b}=x_{a} x_{b}+y_{a} y_{b}\).
proyección escalar	La proyección escalar de un vector sobre otro vector es igual a la longitud de la proyección del primer vector sobre el segundo vector.
vector de unidad	Un vector unitario es un vector con una magnitud de uno.

---

Atribuciones de imagen

1. [Figura 1]
   Crédito: Fundación CK-12
   Fuente: https://commons.wikimedia.org/wiki/File:Prototype_Pontiac_race_car.jpg
   Licencia: CC BY-SA