6.1.2: Ecuación de una elipse
- Page ID
- 108780
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ecuación de una elipse
Ken está teniendo un desacuerdo con su amigo Scott. Scott dice que la pista en la que corren en la escuela no es realmente una elipse, sino un óvalo. Ken piensa que es una distinción tonta, ya que los óvalos y elipses son lo mismo. ¿Quién está en lo correcto?
Ecuación de una elipse
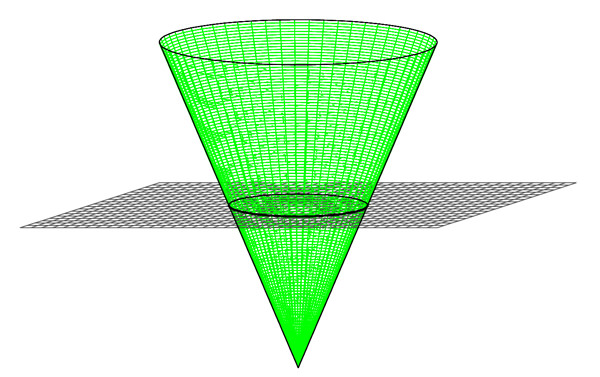
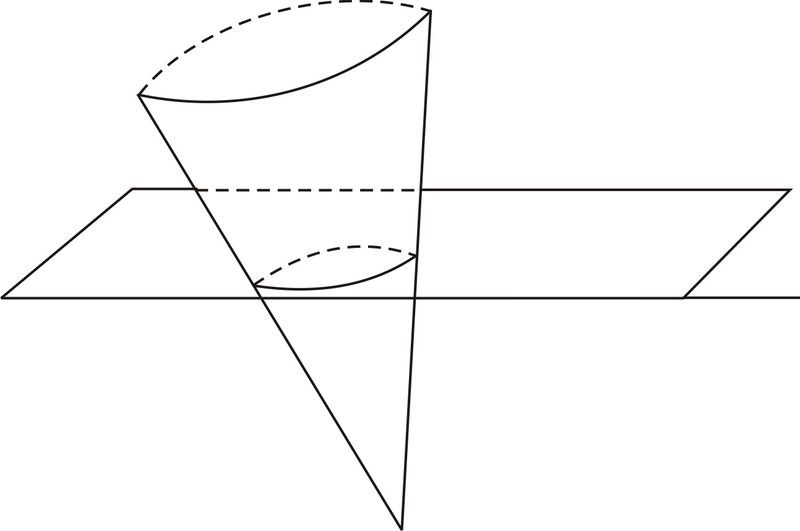
Cuando un avión “corta” un lado de un cono, obtenemos un círculo o un objeto “ovalado” como se muestra a continuación. Resulta que este no es un óvalo ordinario, sino algo llamado elipse, una forma con propiedades especiales.
|
a. Cono “cortado” por un plano 90 o al eje del cono para formar un círculo.
|
b. Cono “cortado” por un plano en ángulo para formar una elipse.
|
|---|
Las elipses se pueden definir por algunas de sus propiedades. Una forma de definir una elipse es como un “círculo estirado”. Es la forma que obtendrías si dibujaras un círculo en un globo desinflado y luego estiras el globo uniformemente en dos direcciones opuestas:

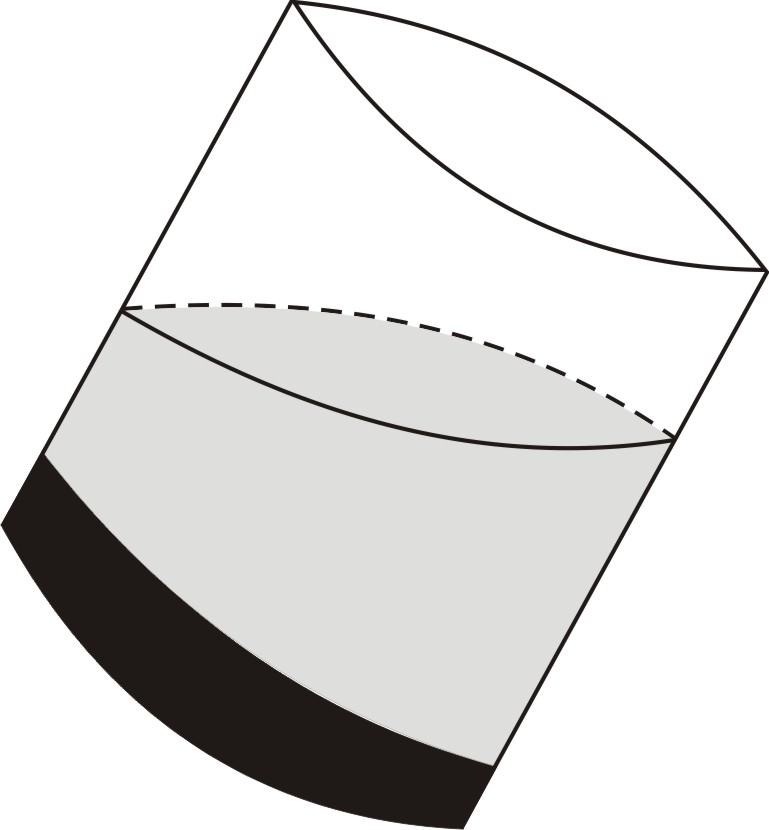
También es la forma de la superficie del agua que resulta cuando inclinas un vaso redondo:
O una elipse podría pensarse como la forma de un círculo dibujado en una hoja de papel cuando se ve en ángulo.
Ecuaciones de Elipses
Este “estiramiento” se puede representar algebraicamente. Para simplificar, tomar el círculo de radio 1 centrado en el origen (0,0). La fórmula de distancia nos dice que este es el conjunto de puntos (x, y) que es una distancia a 1 unidad del origen.
\ (\\ comenzar {alineado}
D &=\ sqrt {\ izquierda (x_ {1} -x_ {2}\ derecha) ^ {2}\ derecha) ^ {2}\ derecha) ^ {2}\ derecha) ^ {2}}\\
1 &=\ sqrt {(x-0) ^ {2} + (y-0) ^ {2}}\\
1 &=x^ {2} +y^ {2}
\ final {alineado}\)
Esta ecuación,\(\ x^{2}+y^{2}=1\), puede ser alterada para estirar el círculo en la dirección horizontal (es decir, eje x) dividiendo la\(\ x\) variable por una constante\(\ a>1\),
\(\ \left(\frac{x}{a}\right)^{2}+y^{2}=1\)
¿Por qué esto estira el círculo horizontalmente? Bueno, el efecto de dividir\(\ x\) por\(\ a\) es que para cada\(\ y\) −valor en un par ordenado\(\ (x, y)\) que satisfaga la ecuación original, el\(\ x\) valor correspondiente debe ser multiplicado por\(\ a\) para que el par haga una solución a la ecuación alterada. Entonces las soluciones\(\ (x, y)\) del círculo están en correspondencia uno a uno con las soluciones\(\ (ax, y)\) de la ecuación alterada, de ahí estirar la gráfica correspondiente a la izquierda y a la derecha por un factor de\(\ a\).
Aquí está la gráfica de\(\ \left(\frac{x}{2}\right)^{2}+y^{2}=1\):
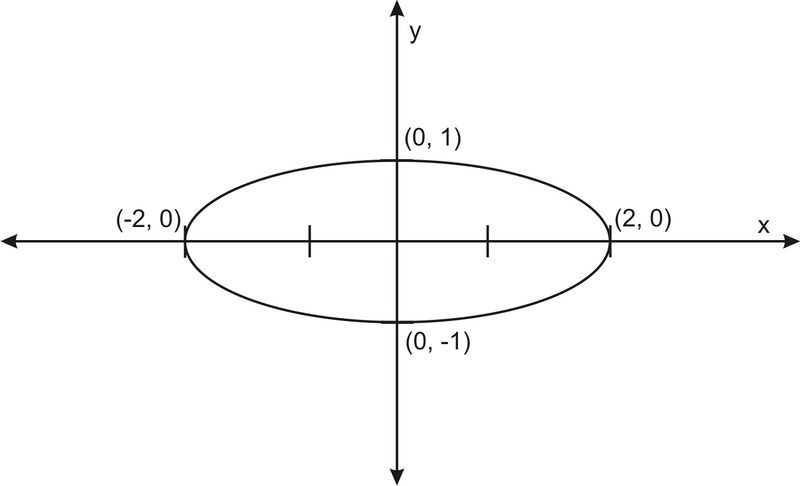
Generalizando la ecuación permitiendo un estiramiento en la dirección vertical, obtenemos lo siguiente.
\(\ \left(\frac{x}{a}\right)^{2}+\left(\frac{y}{b}\right)^{2}=1\)
El factor\(\ a\) estira el círculo en la dirección horizontal y el factor\(\ b\) estira el círculo en la dirección vertical. Si\(\ a=b\), esto es sólo un círculo. Cuando\(\ a \neq b\), esta ecuación representa una elipse. La elipse se estira en la dirección horizontal si\(\ b<a\) y se estira en la dirección vertical si\(\ a<b\).
A menudo, la ecuación anterior se escribe de la siguiente manera.
\(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
A esto se le llama la forma estándar de la ecuación de una elipse, asumiendo que la elipse está centrada en (0, 0).
Para bosquejar una gráfica de una elipse con la ecuación\(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), comience por trazar las intercepciones de cuatro ejes, que son fáciles de encontrar conectando 0 para x y luego para y Luego, dibuje la elipse a mano alzada, o con un programa gráfico o calculadora.
Los Focos
En cada elipse hay dos puntos especiales llamados los focos (los focos son plurales, el foco es singular), que se encuentran dentro de la elipse y que pueden ser utilizados para definir la forma. Para una elipse centrada en (0,0) que es más ancha que alta, su eje mayor es horizontal y sus focos están en\(\ \left(\sqrt{a^{2}-b^{2}}, 0\right)\) y\(\ \left(-\sqrt{a^{2}-b^{2}}, 0\right)\).
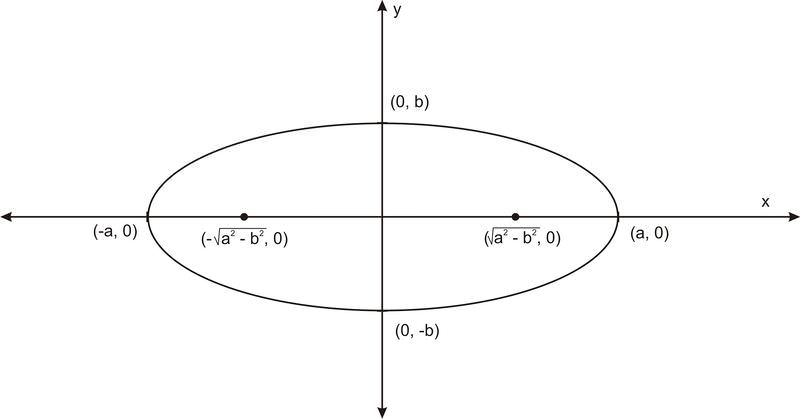
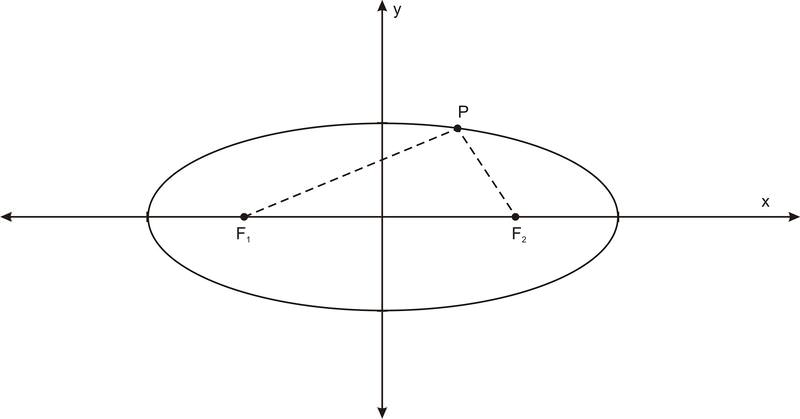
¿Cuál es el significado de estos puntos? Las elipses se relacionan con estos puntos tanto como un círculo se relaciona con su centro. Recuerde que un círculo puede pensarse como el conjunto de puntos en un plano que están a cierta distancia del punto central, de hecho, esa suele ser la definición de círculo. Bueno, los focos actúan como el centro excepto que hay dos de ellos. Una elipse es el conjunto de puntos donde la suma de la distancia entre cada punto de la elipse y cada uno de los dos focos es un número constante. En el diagrama de abajo, para cualquier punto\(\ P\) de la elipse\(\ F_{1} P+F_{2} P=d\),, donde\(\ F_{1}\) y\(\ F_{2}\) son los focos y\(\ d\) es una constante.
Ejemplos
Antes, te hicieron una pregunta sobre el desacuerdo de Ken y Scott.
Solución
Scott está en lo correcto. Los óvalos no son lo mismo que elipses.
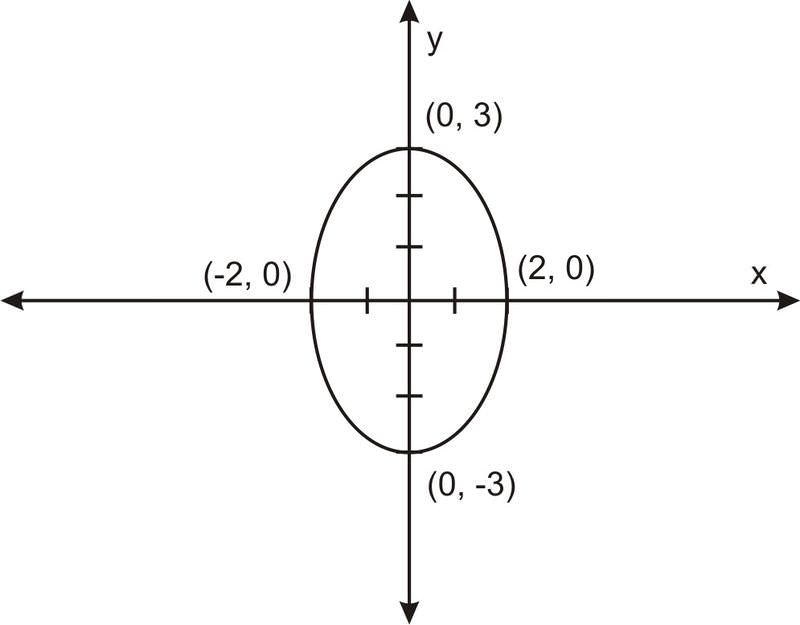
Esbozar la gráfica de\(\ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1\).
Solución
Esta ecuación se puede reescribir como\(\ \frac{x^{2}}{2^{2}}+\frac{y^{2}}{3^{2}}=1\).
Para bosquejar, establecemos\(\ x=0\) y resolvemos\(\ y\) para encontrar las\(\ x\) -intercepciones y establecemos\(\ y=0\) y resolvemos\(\ x\) para encontrar las intercepciones\(\ y\) −.
Los cuatro puntos que obtenemos son (0, 3), (0, -3), (2, 0), y (-2, 0).
Trace esos puntos y dibuje la elipse:
Esbozar la gráfica de\(\ \frac{x^{2}}{16}+y^{2}=1\).
Solución
Esto se puede reescribir como\(\ \frac{x^{2}}{4^{2}}+\frac{y^{2}}{1^{2}}=1\). Después de encontrar las intercepciones y esbozar la gráfica con el mismo proceso anterior, tenemos:
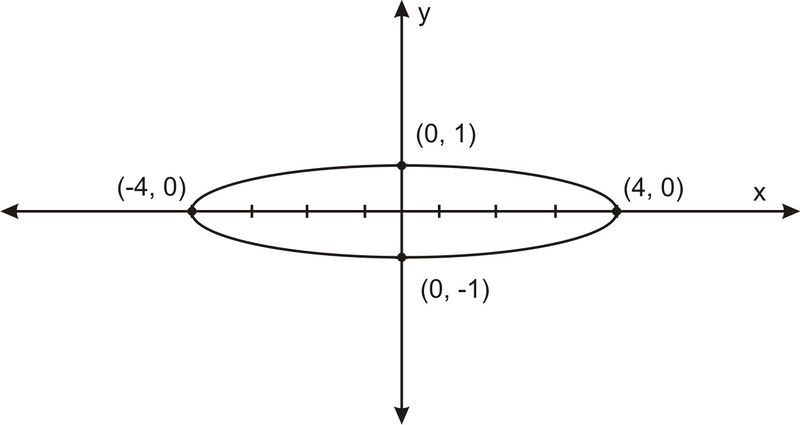
El segmento que abarca la dirección larga de la elipse se llama eje mayor, y el segmento que abarca la dirección corta de la elipse se llama eje menor. Entonces en el último ejemplo el eje mayor es el segmento de (-4, 0) a (4, 0) y el eje menor es el segmento de (0, -1) a (0, 1).
Los ejes mayor y menor son ejemplos de lo que a veces se llaman líneas de referencia. Apolonio, el matemático griego antiguo que escribió un tratado temprano sobre cónicas, utilizó estas y otras líneas de referencia para orientar secciones cónicas. Aunque los griegos no utilizaron un plano de coordenadas para discutir la geometría, estas líneas de referencia ofrecen una perspectiva de encuadre similar al plano cartesiano que usamos hoy en día. La forma de Apolonio de enmarcar cónicas con líneas de referencia fue la matemática más cercana que llegó al sistema de geometría de coordenadas que tan bien conoces hasta el trabajo sistemático de Descartes y Fermat en el siglo XVII.
¿Cuál es el rango completo de la excentricidad de una elipse? ¿Qué aspecto tiene cerca de los extremos de esta gama?
Solución
Los focos se pueden usar para medir qué tan lejos se “estira” una elipse de un círculo. El símbolo\(\ \varepsilon\) representa la excentricidad de una elipse, y se define por la distancia entre los focos dividida por la longitud del eje mayor, o\(\ \frac{\sqrt{a^{2}-b^{2}}}{a}\) por elipses orientadas horizontalmente y\(\ \frac{\sqrt{b^{2}-a^{2}}}{b}\) por elipses orientadas verticalmente. Ya que un círculo es una elipse donde\(\ a=b\), los círculos tienen una excentricidad de 0.
El intervalo de valores posibles es\(\ \varepsilon \in[0,1)\). At\(\ \varepsilon=0\), la elipse es un círculo; a medida que la excentricidad se acerca a 1 se vuelve cada vez más alargada.
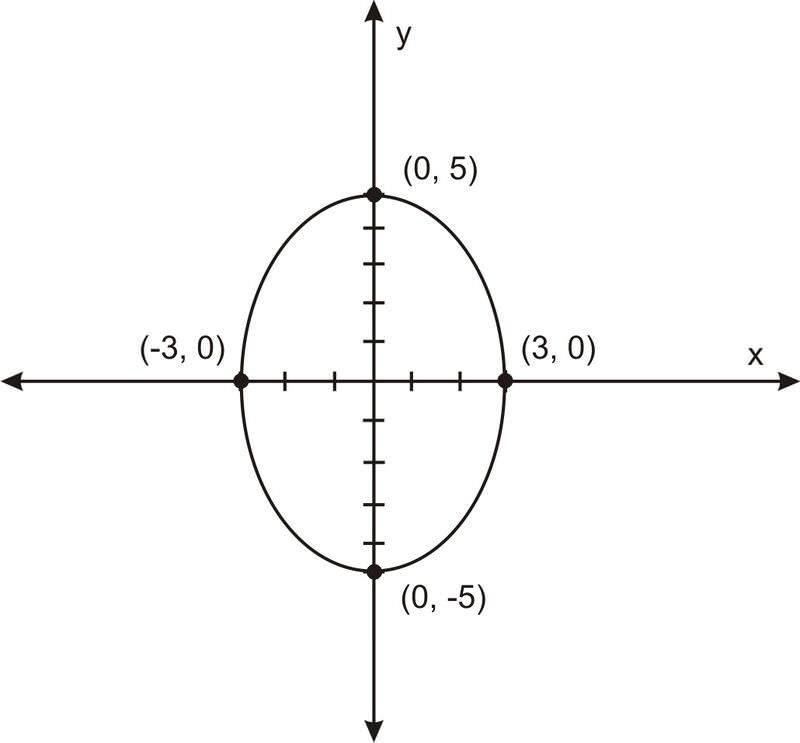
No todas las ecuaciones para elipses comienzan en la forma estándar anterior. Por ejemplo,\(\ 25 x^{2}+9 y^{2}=225\) es una elipse. Ponlo en la forma adecuada y graficarlo.
Solución
Para graficar\(\ 25 x^{2}+9 y^{2}=225\) como elipse:
\(\ \frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)... Primero, divide ambos lados por 225
\(\ \frac{x^{2}}{3^{2}}+\frac{y^{2}}{5^{2}}=1\)... Encuentra las intercepciones
Graficando, contamos con:
Se mencionó anteriormente que cuando se inclina un vaso redondo de agua, la superficie del agua es una elipse. Usando nuestra definición de trabajo de elipse como “círculo estirado”, explica por qué crees que el agua toma esta forma.
Solución
Las respuestas pueden variar, pero deben explicar por qué la forma que resulta estira un círculo en una dirección porque el ancho del vidrio es constante.
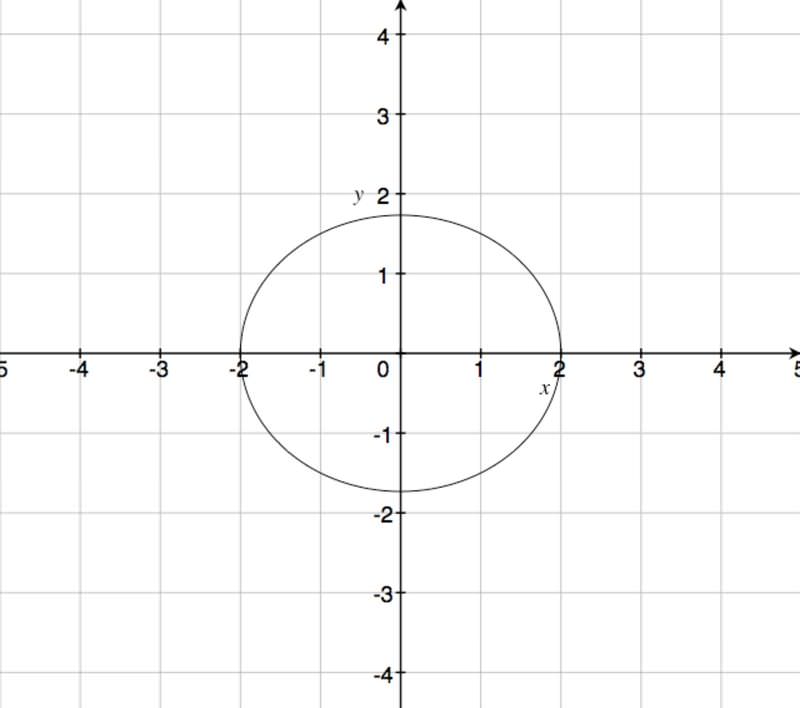
Intenta bosquejar esta elipse donde los números no resulten tan pulcros:\(\ 3 x^{2}+4 y^{2}=12\).
Solución
Para graficar\(\ 3 x^{2}+4 y^{2}=12\):
\(\ \frac{x^{2}}{4}+\frac{y^{2}}{3}=1\)... Primero, divide ambos lados por 12
\(\ \frac{x^{2}}{2^{2}}+\frac{y^{2}}{\sqrt{3}^{2}}=1\)... Encuentra las intercepciones
Graficando, obtenemos:
Revisar
Convierte cada ecuación a la forma estándar de una elipse.
- \(\ x^{2}+4 y^{2}=4\)
- \(\ 9 x^{2}+16 y^{2}=144\)
- \(\ 25 x^{2}+36 y^{2}=900\)
- \(\ 36 x^{2}+9 y^{2}=324\)
- \(\ 49 x^{2}+y^{2}=49\)
- \(\ 16 x^{2}+4 y^{2}=64\)
- \(\ x^{2}+2 y^{2}=2\)
- \(\ 3 x^{2}+4 y^{2}=12\)
- \(\ 5 x^{2}+6 y^{2}=30\)
- \(\ 6 x^{2}+3 y^{2}=18\)
- \(\ 7 x^{2}+y^{2}=7\)
- \(\ 4 x^{2}+2 y^{2}=8\)
Grafica las siguientes elipses.
- \(\ 9 x^{2}+16 y^{2}=144\)
- \(\ 49 x^{2}+y^{2}=49\)
- \(\ x^{2}+2 y^{2}=2\)
- \(\ 7 x^{2}+y^{2}=7\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.1.
El vocabulario
| Término | Definición |
|---|---|
| Cono | Un cono es una figura tridimensional sólida con una base circular y un vértice. |
| Cónico | Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas. |
| Excentricidad | La excentricidad de una sección cónica es una medida de cuánto se desvía la sección cónica de ser circular. La excentricidad de los círculos es 0, la excentricidad de las elipses está entre 0 y 1, la excentricidad de las parábolas es 1, y la excentricidad de las hipérbolas es mayor que 1. Para elipses e hipérbolas,\(\ e=\frac{c}{a}\). |
| Elipse | Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos. |
| Elipses | Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos. |
| Focos | Los focos de una elipse son los dos puntos que definen la elipse. La suma de las distancias desde cualquier punto de la elipse a los focos es constante. |
| Eje Mayor | El eje mayor de una elipse es el diámetro más largo de la elipse. |
| eje menor | El eje menor de una elipse es el diámetro más corto de la elipse. |
| forma estándar | La forma estándar de una elipse centrada en\(\ (h, k)\) es\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). |