6.5.2: Clasificación de Secciones Cónicas
- Page ID
- 108853
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Clasificación de secciones cónicas
Tú y tus amigos están jugando Nombra la Sección Cónica. Tu amigo saca una tarjeta con la ecuación\(\ x^{2}+3 x y=-5 y^{2}-10\) escrita en ella. ¿Qué tipo de sección cónica está representada por la ecuación?
Clasificación de secciones cónicas
Otra forma de clasificar una sección cónica cuando está en la forma general es usar el discriminante, como a partir de la Fórmula Cuadrática. El discriminante es lo que está debajo del radical\(\ b^{2}-4 a c\), y podemos usar esto para determinar si la cónica es una parábola, círculo, elipse o hipérbola. Si la forma general de la ecuación es\(\ A x^{2}+B x y+C y^{2}+D x+E y+F=0\), dónde\(\ B=0\), entonces el discriminante será\(\ B^{2}-4 A C\).
Utilice la siguiente tabla:
| \(\ B^{2}-4 A C=0\)y\(\ A=0\) o\(\ C=0\) | Parábola |
|---|---|
| \(\ B^{2}-4 A C<0\)y\(\ A=C\) | Círculo |
| \(\ B^{2}-4 A C<0\)y\(\ A≠C\) | Elipse |
| \(\ B^{2}-4 A C>0\) | Hipérbola |
Usemos el discriminante para determinar el tipo de sección cónica para las siguientes ecuaciones.
- \(\ x^{2}-4 y^{2}+5 x-8 y+16=0\)
\(\ A=1\),\(\ B=0\), y\(\ C=−4\)
\(\ 0^{2}-4(1)(-4)=16\)Esto es una hipérbola.
- \(\ 3 x^{2}+3 y^{2}-9 x-12 y-20=0\)
\(\ A=3\),\(\ B=0\),\(\ C=3\)
\(\ 0^{2}-4(3)(3)=-36\)Porque\(\ A=C\) y el discriminante es menor que cero, esto es un círculo.
Por último, usemos el discriminante para determinar el tipo de cónico. Luego, cambiaremos la ecuación a forma estándar para verificar nuestra respuesta. También encontraremos el centro (o vértice, si es una parábola).
\(\ x^{2}+y^{2}-6 x+14 y-86=0\)
\(\ A=1\),\(\ B=0\),\(\ C=1\) Esto es un círculo.
\ (\\ comenzar {alineado}
\ izquierda (x^ {2} -6 x+9\ derecha) +\ izquierda (y^ {2} +14 y+49\ derecha) &=86+49+9\\
(x-3) ^ {2} + (y+7) ^ {2} &=144
\ end {alineado}\)El centro es\(\ (3, −7)\).
Ejemplos
Anteriormente, se le pidió que determinara el tipo de sección cónica representada por la ecuación\(\ x^{2}+3 x y=-5 y^{2}-10\).
Solución
Primero tenemos que reescribir la ecuación es forma estándar.
\(\ x^{2}+3 x y=-5 y^{2}-10 x^{2}+3 x y+5 y^{2}+10=0\)
Ahora podemos usar el discriminante para encontrar el tipo de sección cónica representada por la ecuación.
\(\ A=1\),\(\ B=3\),\(\ C=5\)
\(\ 3^{2}-4(1)(5)=-11\)Porque\(\ A≠C\) y el discriminante es menor que cero, esta ecuación representa una elipse.
Para los Ejemplos 2 y 3, use el discriminante para determinar el tipo de cónico.
\(\ 2 x^{2}+5 y^{2}-8 x+25 y+115=0\)
Solución
\(\ 0^{2}-4(2)(5)=-40\), esto es una elipse.
\(\ 5 y^{2}-9 x-10 y-14=0\)
Solución
\(\ 0^{2}-4(0)(5)=0\), esto es una parábola.
Utilizar el discriminante para determinar el tipo de cónico. Luego, cambia la ecuación a forma estándar para verificar tu respuesta. Encuentra el centro o vértice, si es una parábola.
Solución
\(\ -4 x^{2}+3 y^{2}-8 x+24 y+32=0\)
\(\ 0^{2}-4(-4)(3)=48\), esto es una hipérbola. Cambiándolo a forma estándar, tenemos:
\ (\\ comenzar {alineado}
\ izquierda (-4 x^ {2} -8 x\ derecha) +\ izquierda (3 y^ {2} +24 y\ derecha) &=-32\\
-4\ izquierda (x^ {2} +2 x+1\ derecha) +3\ izquierda (y^ {2} +8 y+16\ derecha) &=-32+48-4\
-4 (x+1) ^ {2} +3 (y+4) ^ {2} &=12\\
\ frac {- (x+1) ^ {2}} {3} +\ frac {(y+4) ^ {2}} {4} &=1
\ end {alineado}\)
Por lo general, escribimos el término negativo segundo, así es la ecuación\(\ \frac{(y+4)^{2}}{4}-\frac{(x+1)^{2}}{3}=1\). El centro es\(\ (-1,-4)\).
Revisar
Utilice el discriminante para determinar el tipo de cónica que representa cada ecuación.
- \(\ 2 x^{2}+2 y^{2}+16 x-8 y+25=0\)
- \(\ x^{2}-y^{2}-2 x+5 y-12=0\)
- \(\ 6 x^{2}+y^{2}-12 x+7 y+35=0\)
- \(\ 3 x^{2}-15 x+9 y-18=0\)
- \(\ 10 y^{2}+6 x-40 y+253=0\)
- \(\ 4 x^{2}+4 y^{2}+32 x+48 y+465=0\)
Coincidir la ecuación con la gráfica correcta.
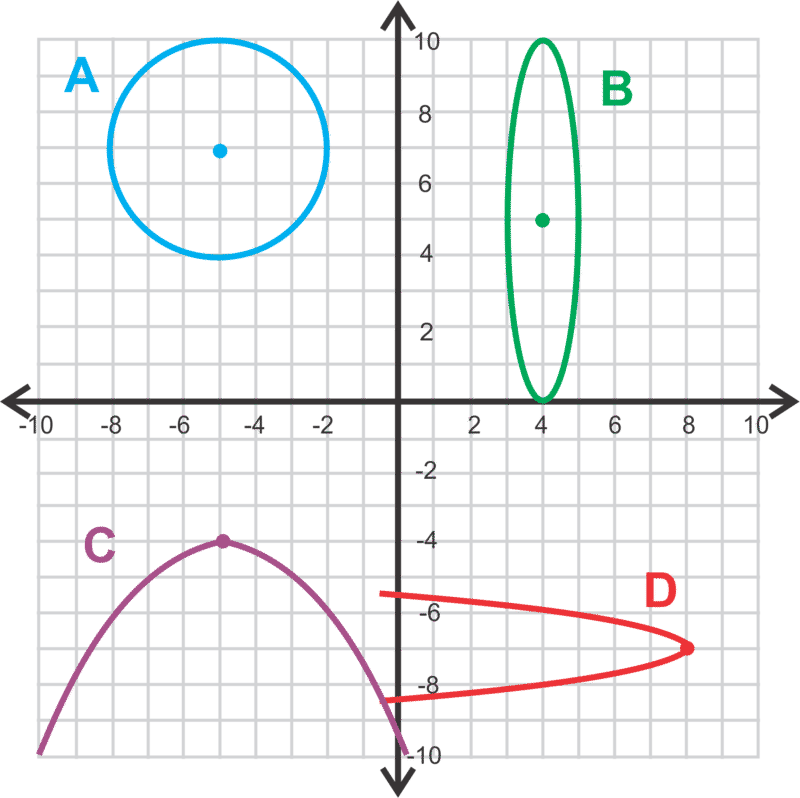
- \(\ x^{2}+10 x+4 y+41=0\)
- \(\ 4 y^{2}+x+56 y+188=0\)
- \(\ x^{2}+y^{2}+10 x-14 y+65=0\)
- \(\ 25 x^{2}+y^{2}-200 x-10 y+400=0\)
Utilizar el discriminante para determinar el tipo de cónico. Luego, cambia la ecuación a forma estándar para verificar tu respuesta. Encuentra el centro o vértice, si es una parábola.
- \(\ x^{2}-12 x+6 y+66=0\)
- \(\ x^{2}+y^{2}+2 x+2 y-2=0\)
- \(\ x^{2}-y^{2}-10 x-10 y-10=0\)
- \(\ y^{2}-10 x+8 y+46=0\)
- Encuentra el Área de una Gráfica Elipse\(\ x^{2}+y^{2}=36\) y encuentra su área.
- Después, grafica\(\ \frac{x^{2}}{36}+\frac{y^{2}}{25}=1\) y\(\ \frac{x^{2}}{25}+\frac{y^{2}}{36}=1\) sobre los mismos ejes.
- ¿Estas elipses tienen la misma área? ¿Por qué o por qué no?
- Si la ecuación del área de un círculo es\(\ A=\pi r^{2}\), ¿cuál crees que es el área de una elipse? Uso\(\ a\) y\(\ b\) como en la forma estándar,\(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\).
- Encuentra las áreas de las elipses de la parte a. ¿Son las áreas más o menos que el área del círculo? ¿Por qué o por qué no?
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.11.
Atribuciones de imagen
- [Figura 1]
Crédito: Pbroks13; Fundación CK-12
Fuente: https://commons.wikimedia.org/wiki/File:Conic_sections_with_plane.svg; GeoGebra