2.9: Proyecciones de mapa

¿Cómo cambia Groenlandia de tamaño?

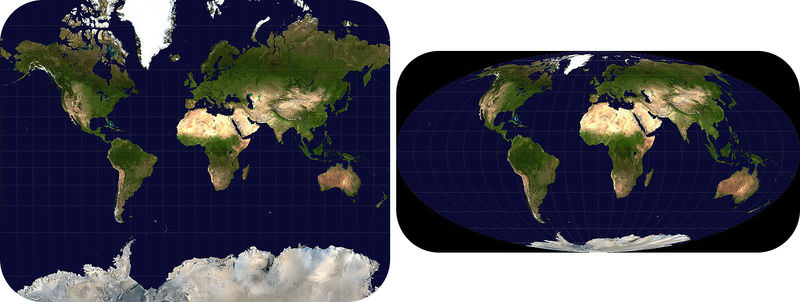
¡Groenlandia no cambia de tamaño! Diferentes proyecciones de mapas hacen que Groenlandia parezca tener un tamaño diferente. La proyección de Mercator hace que todo lo que está cerca de las áreas polares parezca demasiado grande. La proyección Mollweide distorsiona mucho menos el tamaño de las regiones polares. Para ver el tamaño real de Groenlandia, mira un globo terráqueo.

Proyecciones de mapas

La Tierra es una bola redonda y tridimensional. En un área pequeña, la Tierra se ve plana, por lo que no es difícil hacer mapas precisos de un lugar pequeño. Cuando los cartólogos quieren mapear la Tierra redonda en papel plano, utilizan proyecciones. ¿Qué pasa si intentas aplanar la piel de una naranja pelada? ¿O si intentas envolver un balón de fútbol para regalo? Para aplanar, la cáscara de naranja debe rasgarse, y su forma debe distorsionarse. Para envolver un objeto redondo con papel plano requiere muchos cortes y pliegues adicionales. Una proyección es una manera de representar la superficie curva de la Tierra sobre papel plano (Figura abajo).

Una proyección de mapa traduce la superficie curva de la Tierra en dos dimensiones.

Hay muchos tipos de proyecciones. Cada uno usa una manera diferente de cambiar tres dimensiones en dos dimensiones.

Hay dos métodos básicos que los creadores de mapas utilizan en las proyecciones:

• El cartólogo “corta” la esfera de alguna manera y la despliega para hacer un mapa plano. Esto es como aplanar una cáscara de naranja.
• El creador de mapas puede mirar la esfera desde cierto punto y luego traducir esta vista en un papel plano.

Veamos algunas proyecciones de uso común.

Proyección Mercator

En 1569, Gerardus Mercator (1512-1594) (Figura abajo) descubrió una manera de hacer un mapa plano de nuestro mundo redondo. A esto se le llama la proyección de Mercator.

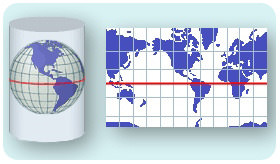
Imagínese envolver la Tierra redonda en forma de bola con un trozo de papel grande y plano. Primero haces un tubo o un cilindro. El cilindro toca la Tierra en el Ecuador. Los polos son los puntos más alejados del cilindro. Ahora haz brillar una luz desde el interior de tu modelo Tierra hacia el cilindro. La imagen proyectada sobre el papel es una proyección de Mercator. ¿Dónde representa mejor la proyección a la Tierra? ¿Dónde está peor? Tu mapa sería el más correcto en el Ecuador. Las formas y tamaños de los continentes se estiran más cerca de los polos. Los primeros marineros y navegantes encontraron útil el mapa de Mercator porque la mayoría de las exploraciones se ubicaron cerca del Ecuador. Muchos mapas del mundo todavía utilizan la proyección de Mercator.

Una proyección de Mercator traduce la superficie curva de la Tierra en un cilindro.

La proyección de Mercator se encuentra mejor dentro de los 15° al norte o al sur del Ecuador. Las masas de tierra o países fuera de esa zona se estiran fuera de forma. Cuanto más lejos esté la característica del Ecuador, más fuera de forma se estira. Por ejemplo, si miras a Groenlandia en un globo, ves que es un país relativamente pequeño cerca del Polo Norte. Pero mira la proyección de Mercator arriba. Groenlandia parece casi tan grande como Estados Unidos. Debido a que Groenlandia está más cerca del polo, la forma y el tamaño del continente se incrementan considerablemente. Estados Unidos está más cerca de sus verdaderas dimensiones. ¿Por qué es esto cierto?

En una proyección de Mercator, todas las direcciones de la brújula son líneas rectas. Esto lo convierte en un buen tipo de mapa para la navegación. La parte superior del mapa es norte, la parte inferior es sur, el lado izquierdo es oeste y el lado derecho es este. Sin embargo, debido a que es un mapa plano de una superficie curva, una línea recta en el mapa no es la distancia más corta entre los dos puntos que conecta.

Proyección Cónica

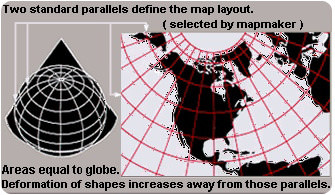
En lugar de un cilindro, podrías envolver el papel plano en un cono. Las proyecciones de mapa cónico utilizan una forma de cono para representar mejor las regiones cercanas a los polos (Figura a continuación). Las proyecciones cónicas son las mejores donde la forma del cono toca el globo terráqueo. Esto es a lo largo de una línea de latitud, generalmente el Ecuador.

Una proyección de mapa cónico envuelve la Tierra con una forma de cono en lugar de un cilindro.

Proyección gnomónica

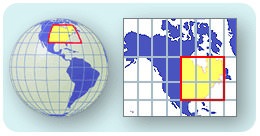
¿Y si quieres un enfoque diferente? Digamos que no quieres envolver un trozo de papel plano alrededor de un objeto redondo. Podrías poner un trozo de papel plano justo en el área que quieras mapear. Este tipo de mapa se denomina proyección de mapa gnomónico (Figura a continuación). El papel toca la Tierra sólo en un punto. Los tamaños y formas de los países cercanos a ese punto son buenos. Los polos suelen ser mapeados de esta manera para evitar distorsiones. Una proyección gnómica es mejor para su uso en un área pequeña.

Una proyección gnomónica coloca un trozo de papel plano sobre un punto en algún lugar de la Tierra y proyecta una imagen a partir de ese punto.

Proyección Robinson

En 1963, Arthur Robinson hizo un mapa con tamaños y formas más precisos de áreas terrestres. Lo hizo usando fórmulas matemáticas. Las fórmulas podrían traducir directamente las coordenadas en el mapa. Este tipo de proyección tiene la forma de un óvalo en lugar de un rectángulo (Figura a continuación).

Una proyección Robinson representa mejor las verdaderas formas y tamaños de las áreas de tierra.

El mapa de Robinson es más preciso que una proyección de Mercator. Las formas y tamaños de los continentes están más cerca de la verdad. El mapa de Robinson está mejor dentro de 45° del Ecuador. Las distancias a lo largo del Ecuador y las líneas paralelas a él son ciertas. Sin embargo, las escalas a lo largo de cada línea de latitud son diferentes. En 1988, la National Geographic Society comenzó a utilizar la proyección de Robinson para sus mapas mundiales.

Resumen

• Una proyección de mapa es una manera de mostrar una figura tridimensional en dos dimensiones.
• Todas las proyecciones de mapas tienen cierta distorsión. Diferentes tipos tienen distorsiones en diferentes ubicaciones y de diferentes cantidades.
• El proyecto de Robinson es diferente al resto porque utiliza fórmulas matemáticas. Otras proyecciones son las mejores en un punto.

Revisar

1. ¿Por qué una proyección de mapa distorsiona las características de la Tierra? ¿Dónde distorsiona más las características?
2. ¿Qué tipo de proyección es mejor para alguien interesado en estudiar Groenlandia? ¿Lo peor?
3. ¿Por qué la proyección de Mercator habría estado bien para su uso en el siglo XVI?

Explora más

Utilice el siguiente recurso para responder a las preguntas que siguen.

1. ¿Cómo es hacer un mapa de la Tierra como tratar de aplanar una cáscara de naranja? ¿Qué problemas ocurren al hacer un mapa de la Tierra?
2. ¿Cuál es la elección que necesitas hacer cuando creas o usas un mapa del mundo?
3. En una Proyección Mercator, ¿qué es exacto y qué no? ¿Qué fue un mapa de Mercator hecho para poder hacer?
4. En Proyección Cilíndrica de Lambert, ¿dónde es mayor la distorsión? ¿Qué es bueno? ¿Qué está distorsionado?
5. En la Proyección Winkel Tripel, ¿cuáles son las tres cosas que hay que comprometer?
6. ¿Qué es una proyección Dymaxion buena para mostrar y para qué se usa comúnmente?
7. ¿Cuál es el mejor tipo de mapa?