1.20: Clasificación de polígonos en el plano de coordenadas
- Page ID
- 107632

Parker está tomando su primera clase de dibujo, aunque no tiene grandes esperanzas. Cuando entra a clase el primer día, su maestra de arte saca una foto de un paisaje urbano y les dice que todos podrán dibujar esto al final de la semana. Su maestra les da a cada uno una copia de esta imagen y les dice que su primera tarea es romper la imagen en sus formas subyacentes. Parker está completamente confundido y abrumado. ¿Cómo puede Parker descubrir cómo romper la imagen en formas?
En este concepto, aprenderás a graficar figuras geométricas dadas coordenadas de vértices e identificar figuras gráficas.
Clasificación de polígonos en el plano de coordenadas
Una cuadrícula de coordenadas es una cuadrícula en la que se grafican los puntos. Por lo general, tiene dos o más líneas de intersección que dividen un plano en cuadrantes, y en las que se definen pares ordenados, o coordenadas. Por lo general, tiene cuatro cuadrantes, o secciones, a la misma.
 Figura\(\PageIndex{2}\)
Figura\(\PageIndex{2}\)El origen es el lugar donde se cruzan las dos líneas. Sus coordenadas se definen como\((0,0)\).
El \(x\)eje -es la línea que va de izquierda a derecha que tiene los números definidos en él y generalmente se etiqueta con un "\(x\)”. La\(x\) coordenada -de un par ordenado se encuentra con relación a ella. Todos los puntos ubicados en el\(x\) eje -tienen una\(y\) coordenada -de 0.
El \(y\)eje -es la línea central que corre arriba-abajo y está etiquetada con un "\(y\)”. Las coordenadas Y se trazan en referencia a este eje. Nuevamente, todas las\(x\) coordenadas -de los puntos ubicados en el\(y\) eje -son 0.
Un par ordenado es una lista de dos números entre paréntesis, separados por una coma como esta:\((5,-3)\). Cuenta dónde se encuentra un punto en el plano de coordenadas. El primer número es la\(x\) coordenada. Te dice a dónde ir en el\(x\) eje -eje. Si es positivo, vas a la derecha. Si es negativo, vas a la izquierda. El segundo número es la coordenada y. Te dice a dónde ir en el\(y\) eje -eje. Si es positivo, subes. Si es negativo, baja.
El vértice de una forma es el lugar donde dos lados de la forma se unen. En general, cuando una forma se define dentro de un plano de coordenadas, se define por los vértices, y luego se dibujan las líneas para conectarlos.
Un polígono es cualquier forma compuesta por líneas rectilíneas o rectas. El polígono más pequeño es un triángulo, que tiene tres lados. Una figura de cinco lados es un pentágono. Y también se nombran muchos polígonos con más lados que cinco.
Un ángulo recto es un ángulo que parece donde se encuentran los ejes en el plano de coordenadas.
Las líneas paralelas son líneas que durarán para siempre pero que nunca convergerán.
La categoría de polígonos de cuatro lados incluye:
- el cuadrado, que tiene cuatro lados de igual longitud y sus ángulos son todos ángulos rectos;
- el rombo que, como el cuadrado, tiene cuatro lados iguales, pero es “tilty”;
- el rectángulo que tiene dos pares de lados iguales y todos sus ángulos son ángulos rectos;
- el trapecio que puede no tener lados iguales, pero tiene dos líneas que son paralelas; y
- el paralelogramo que tiene dos conjuntos de líneas paralelas que son iguales en longitud entre sí (pero como el rombo, es “tilty”).
Para graficar una figura en el plano de coordenadas, solo tienes que graficar cada uno de los vértices y luego conectarlos con líneas rectas para que ninguna de las líneas se cruce. El número de lados que tienes es el mismo que el número de vértices. Entonces un triángulo, por ejemplo, se define con tres vértices.
Aquí hay un ejemplo.
Grafica una figura con las coordenadas\(A(−4, 3) B(2, 3) C(2,−1) D(−4,−1)\). Cuando termine, nombra la figura que se ha dibujado en la cuadrícula.
Primero, traza cada punto en la cuadrícula de coordenadas y luego conecta las líneas.
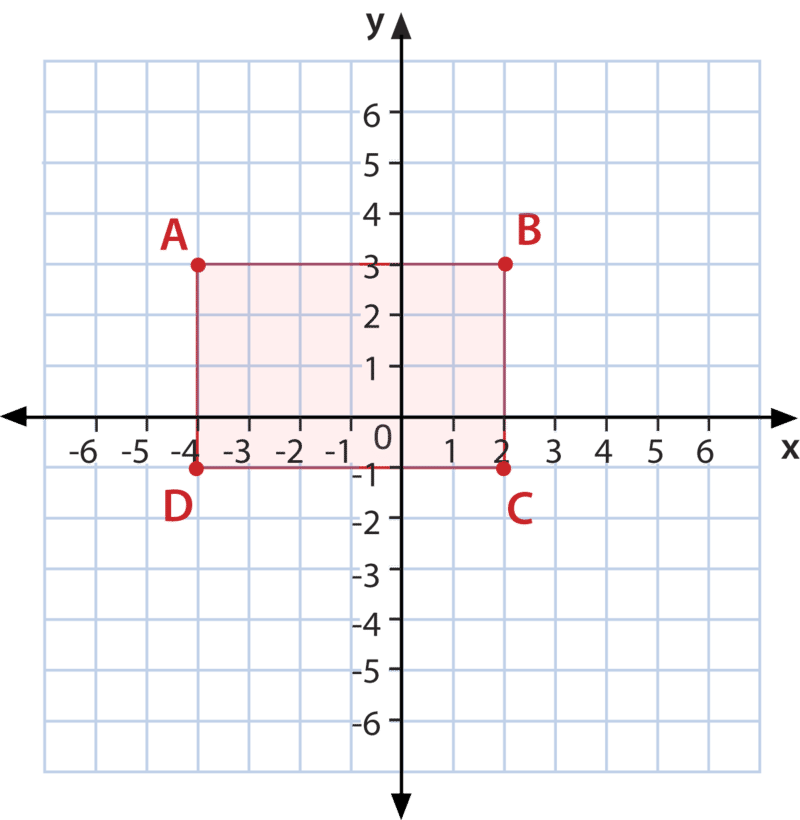 Figura\(\PageIndex{3}\)
Figura\(\PageIndex{3}\)A continuación, para determinar qué tipo de forma es, primero cuente el número de vértices.
Esta figura tiene cuatro, por lo que es una de las formas de cuatro lados.
Entonces, mira para ver cuántos de los lados son iguales.
En este caso, lado\(AB=DC\) y\(AD=BC\). Dado que hay dos conjuntos de lados iguales, esto es un rectángulo o un paralelogramo.
Por último, revisa los ángulos.
En esta forma, los ángulos son ángulos rectos, por lo que este es un rectángulo.
Aquí hay otro ejemplo.
Grafica y nombra la siguiente figura con estas coordenadas\(D(1,3) E(5,3) F(7,−1) G(1,−1)\).
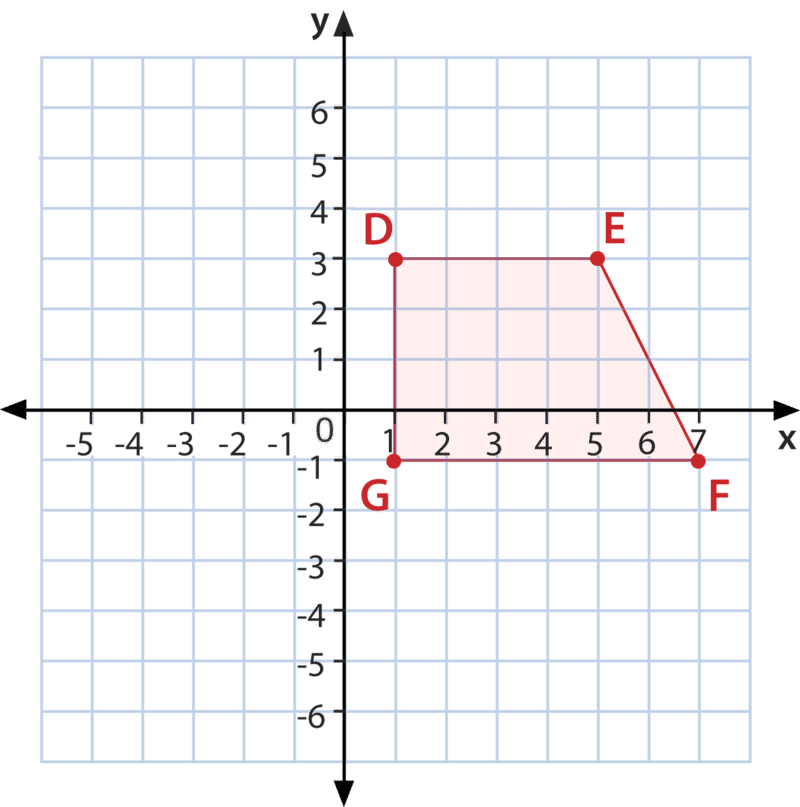 Figura\(\PageIndex{4}\)
Figura\(\PageIndex{4}\)Primero, trazar los vértices y conectarlos.
A continuación, cuente el número de vértices.
Hay cuatro, por lo que esta es una figura de cuatro lados, que se puede ver por su forma.
Entonces, mira a los lados.
Ninguno de los lados tiene la misma longitud, por lo que esta forma debe ser un trapecio.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Parker y su ataque de pánico matemática.
Su maestra de arte le da una imagen de edificios en perspectiva y le dice que la rompa en sus formas constituyentes.
Solución
Primero, dibuja un\(y\) eje por el centro del edificio trasero en la imagen, que se ve aproximadamente a la mitad de la imagen. Entonces, dibuja el\(x\) eje -como la línea del horizonte.
A continuación, entrecerró los ojos ante la imagen e intenta verla no como edificios, sino como formas, en cambio. En el lado derecho de la imagen, se da cuenta de que los edificios forman un triángulo con un vértice comenzando por el origen. Y a la izquierda del\(y\) eje -eje, el otro lado de los edificios hacen otro triángulo, también con un vértice en el origen. Incluso la calle, se da cuenta, hace su propio triángulo, nuevamente con un vértice en el origen. Y entonces el cielo lo termina con un cuarto triángulo con un vértice en el origen.
Entonces, ve que el resto de la imagen sólo está conformada por rectángulos. Hay uno debajo del triángulo de la calle, y uno en los edificios de la izquierda. Y uno donde está el pequeño edificio trasero.
Parker concluye que podría ser capaz de aprender a dibujar después de todo.
Ejemplo\(\PageIndex{2}\)
Determinar la forma dada por los siguientes vértices.
\((−4,6)(4,6)(0,−6)\)
Solución
Primero, cuente el número de vértices.
En este caso, hay tres vértices. Si hay tres vértices, entonces la forma tiene tres lados.
A continuación, determine qué formas son posibles.
Sólo hay una forma cerrada con tres lados, y eso es un triángulo.
La respuesta es un triángulo.
Ejemplo\(\PageIndex{3}\)
Determinar la forma dada por los siguientes vértices.
\((0,2)(2,0)(0,−3)\)
Solución
Primero, cuente el número de vértices.
En este caso, hay tres vértices. Si hay tres vértices, entonces hay tres lados.
A continuación, determine qué formas son posibles.
Sólo hay una forma cerrada con tres lados, y eso es un triángulo.
La respuesta es un triángulo.
Ejemplo\(\PageIndex{4}\)
Determinar la forma dada por los siguientes vértices.
\((−1,−3)(−5,−3)(−7,1)(−1,1)\)
Solución
Primero, cuente el número de vértices.
En este caso, hay cuatro vértices. Si hay cuatro vértices, entonces la forma tiene cuatro lados.
A continuación, determine qué formas son posibles.
Las figuras de cuatro lados son: cuadrado, rombo, trapecio, rectángulo y paralelogramo.
Después, trazar los vértices en un plano de coordenadas.
Después, determinar las propiedades de la forma.
En este caso, la forma tiene dos líneas paralelas y dos líneas no parralel. La única figura de cuatro lados en la que ese es el caso es el trapezoide.
La respuesta es un trapecio.
Ejemplo\(\PageIndex{5}\)
Determinar la forma dada por los siguientes vértices.
\((3,3)(0,3)(0,0)(3,0)\)
Solución
Primero, cuente el número de vértices.
En este caso, hay cuatro vértices. Si hay cuatro vértices, entonces la forma tiene cuatro lados.
A continuación, determine qué formas son posibles.
Las figuras de cuatro lados son: cuadrado, rombo, trapecio, rectángulo y paralelogramo.
Después, trazar los vértices en un plano de coordenadas.
Después, determinar las propiedades de la forma.
En este caso, la forma tiene dos conjuntos de líneas paralelas y y todos los lados tienen la misma longitud. Adicionalmente, la forma tiene cuatro ángulos rectos. El cuadrado es la forma que cumple con estos criterios.
La respuesta es un cuadrado.
Revisar
Grafica cada figura usando los vértices. Entonces nombra la figura graficada.
- \(A(−2,2);B(2,2);C(2,−2);D(−2,−2)\)
- \(D(−4,3);E(−1,1);F(−4,1)\)
- \((1,1)(2,3)(4,1)\)
- \((−1,3)(−5,3)(−1,0)(−5,0)\)
- \((0,5)(3,5)(0,9)(3,9)\)
- \((0,6)(2,6)(0,10)(2,10)\)
- \((−3,6)(6,0)(9,0)\)
- \((−1,6)(−1,8)(−9,6)(−9,8)\)
- \((0,−8)(1,−5)(5,−5)(4,−8)\)
- \((12,0)(12,6)(7,0)\)
Para 11 - 15 dibuja cinco de tus propias figuras en una cuadrícula de coordenadas. Escribe cada conjunto de coordenadas y trabaja con un compañero para identificar cada figura usando solo las coordenadas.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.15.
El vocabulario
| Término | Definición |
|---|---|
| \(x\)-eje | El\(x\) eje -es el eje horizontal en el plano de coordenadas, que comúnmente representa el valor de la variable de entrada o independiente. |
| eje y | El\(y\) eje -es la recta numérica vertical del plano cartesiano. |
| Coordenadas | Las coordenadas de un punto representan la ubicación del punto en el plano cartesiano. Las coordenadas se escriben en pares ordenados:\(x,y)\). |
| Par Pedido | Un par ordenado,\(x,y)\), describe la ubicación de un punto en una cuadrícula de coordenadas. |
| Origen | El origen es el punto de intersección de los ejes x e y en el plano cartesiano. Las coordenadas del origen son\((0, 0)\). |
| Cuadrantes | Un cuadrante es un cuarto del plano de coordenadas. Los cuatro cuadrantes se numeran usando los números romanos I, II, III y IV, comenzando en la parte superior derecha y aumentando en sentido antihorario. |
Recursos adicionales
Elemento interactivo
Vídeo: Trazado de puntos en el plano de coordenadas
Práctica: Clasificación de polígonos en el plano de coordenadas

