1.1: Términos de geometría
- Page ID
- 107647
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Definir y usar términos, incluyendo puntos, líneas, planos, espacio y postulados.
Definiciones geométricas
Un punto es una ubicación exacta en el espacio. Describe una ubicación, pero no tiene tamaño. A continuación se muestran ejemplos:
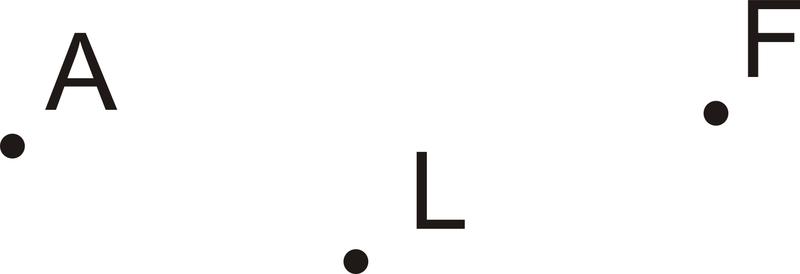
| Etiquetarlo | Dilo |
|---|---|
| \(A\) | punto\(A\) |
Una línea es infinitamente muchos puntos que se extienden para siempre en ambas direcciones. Las líneas tienen dirección y ubicación y siempre son rectas.

Figura\(\PageIndex{2}\)
| Label It | Say It |
|---|---|
| line \(g\) | line \(g\) |
| \(\overleftrightarrow{PQ}\) | line \(PQ\) |
A plane is a flat surface that contains infinitely many intersecting lines that extend forever in all directions. Think of a plane as a huge sheet of paper with no thickness that goes on forever.
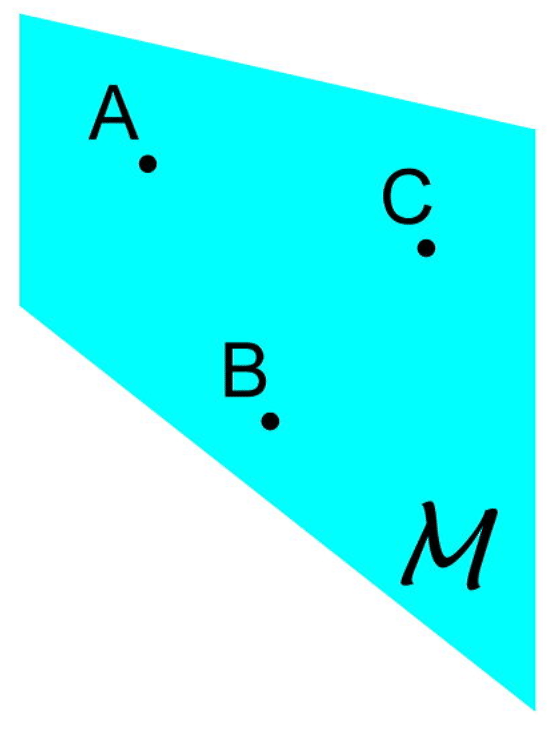
| Label It | Say It |
|---|---|
| Plane \(M\) | Plane \(M\) |
| Plane \(ABC\) | Plane \(ABC\) |
We can use point, line, and plane to define new terms.
Space is the set of all points extending in three dimensions. Think back to the plane. It extended in two dimensions, what we think of as up/down and left/right. If we add a third dimension, one that is perpendicular to the other two, we arrive at three-dimensional space.
Points that lie on the same line are collinear. \(P\),\(Q\),\(R\),\(S\), and \(T\) are collinear because they are all on line \(w\). If a point U were located above or below line w, it would be non-collinear.

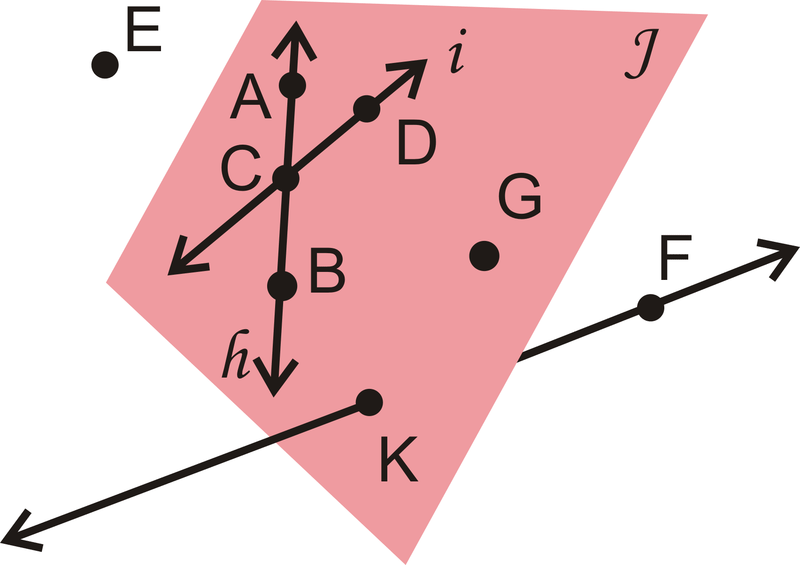
Points and/or lines within the same plane are coplanar. Lines h and i, and points \(A\),\(B\),\(C\),\(D\),\(G\), and \(K\) are coplanar in Plane \(J\). Line \(\overleftrightarrow{KF}\) and point \(E\) are non-coplanar with Plane \(J\).
An endpoint is a point at the end of a line segment. A line segment is a portion of a line with two endpoints. Or, it is a finite part of a line that stops at both ends. Line segments are labeled by their endpoints. Order does not matter.

| Label It | Say It |
|---|---|
| \(\overline{AB}\) | Segment \(AB\) |
| \(\overline{BA}\) | Segment \(BA\) |
A ray is a part of a line. It begins with an endpoint and extends forever away from the endpoint in one direction, perfectly straight. A ray is labeled by its endpoint and one other point on the ray. For rays, order does matter. When labeling, put the endpoint under the side WITHOUT the arrow.
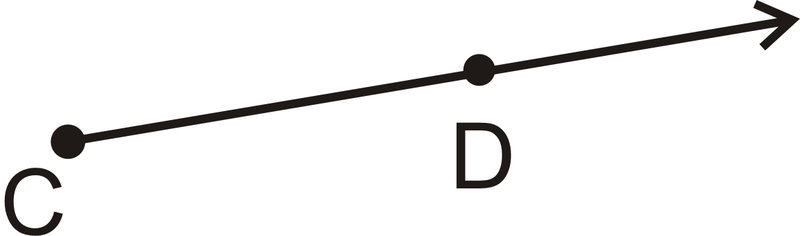
| Label It | Say It |
|---|---|
| \(\overrightarrow{CD}\) | Ray \(CD\) |
| \(\overleftarrow{DC}\) | Ray \(CD\) |
An intersection is a point or set of points where lines, planes, segments, or rays overlap.
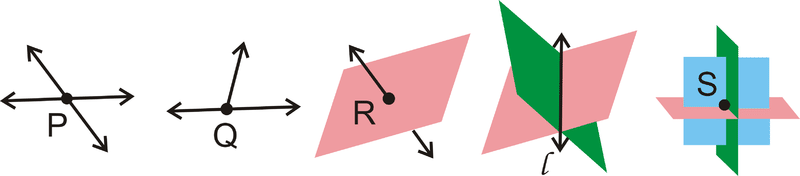
Postulates
A postulate is a basic rule of geometry. Postulates are assumed to be true (rather than proven), much like definitions. The following is a list of some basic postulates.
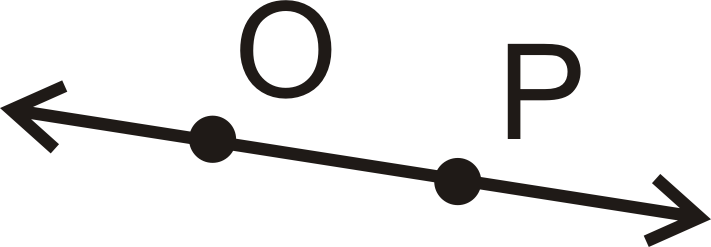
Postulate #1: Given any two distinct points, there is exactly one (straight) line containing those two points.
Postulate #2: Given any three non-collinear points, there is exactly one plane containing those three points.

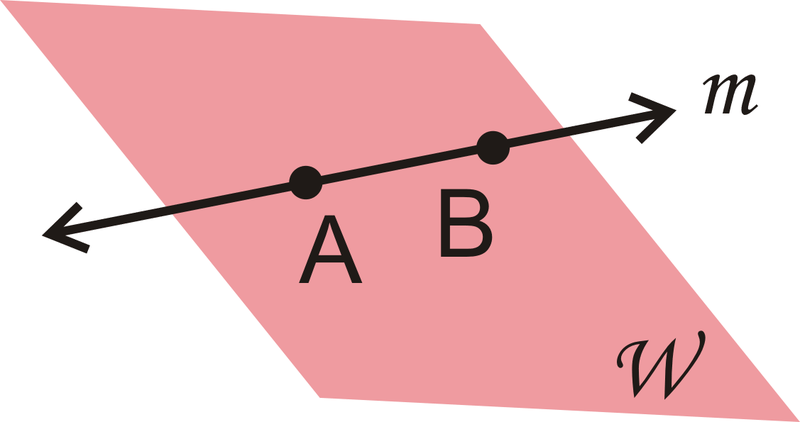
Postulate #3: If a line and a plane share two points, then the entire line lies within the plane.
Postulate #4: If two distinct lines intersect, the intersection will be one point.
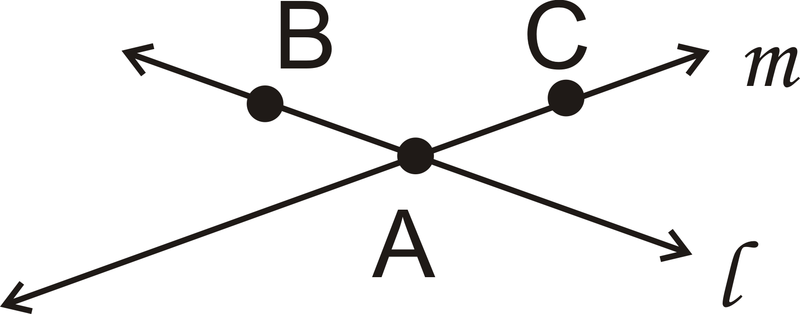
Lines \(I\) and \(m\) intersect at point \(A\).
Postulate #5: If two distinct planes intersect, the intersection will be a line.
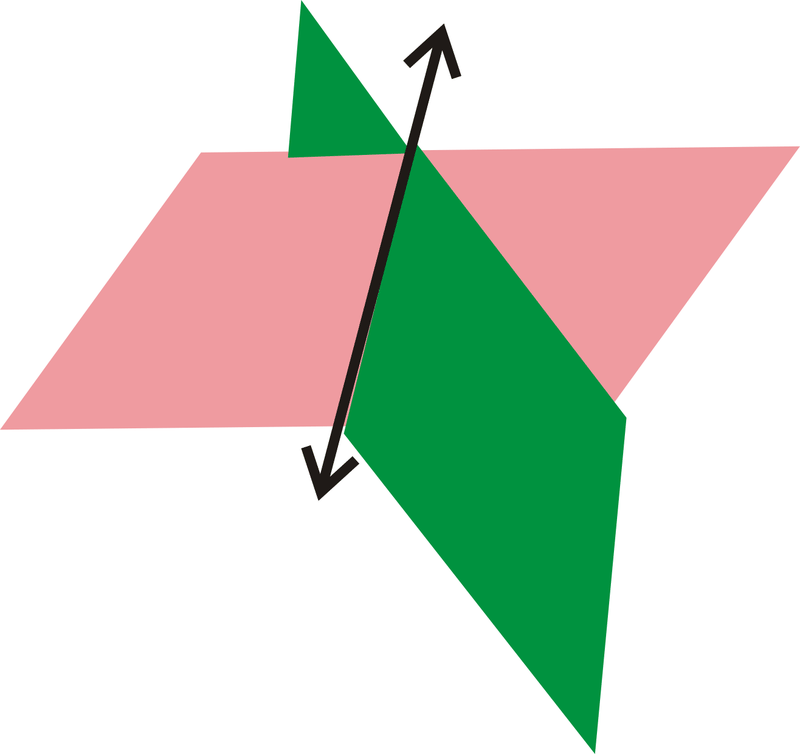
Figure \(\PageIndex{13}\)
When making geometric drawings, be sure to be clear and label all points and lines.
What if you were given a picture of a figure or object, like a map with cities and roads marked on it? How could you explain that picture geometrically?
Example \(\PageIndex{1}\)
What best describes San Diego, California on a globe: point, line, or plane?
Solution
A city is usually labeled with a dot, or point, on a globe.
Example \(\PageIndex{2}\)
Use the picture below to answer these questions.

Figura\(\PageIndex{14}\)
- Enumere otra forma de etiquetar Plano\(J\).
- Enumere otra forma de etiquetar la línea\(h\).
- ¿Son\(K\) y\(F\) colineales?
- ¿Son\(E\),\(B\) y\(F\) coplanares?
Solución
- \(BDG\)El avión es una posibilidad. Cualquier combinación de tres puntos coplanares que no sean colineales sería correcta.
- \(\overleftrightarrow{AB}\). Cualquier combinación de dos de las letras\(A\)\(B\),, o también\(C\) sería correcta.
- Sí, ambos se acuestan\(\overleftrightarrow{KF}\).
- Sí, aunque no\(E\) esté en Plano\(J\), tres puntos cualesquiera hacen un plano distinto. Por lo tanto, los tres puntos crean Plano\(EBF\).
Ejemplo\(\PageIndex{3}\)
¿Qué describe mejor una carretera recta que comienza en una ciudad y se detiene en una segunda ciudad: rayo, línea, segmento o avión?
Solución
El camino recto conecta dos ciudades, que son como puntos finales. El mejor término es segmento.
Ejemplo\(\PageIndex{4}\)
Responde las siguientes preguntas sobre la imagen.
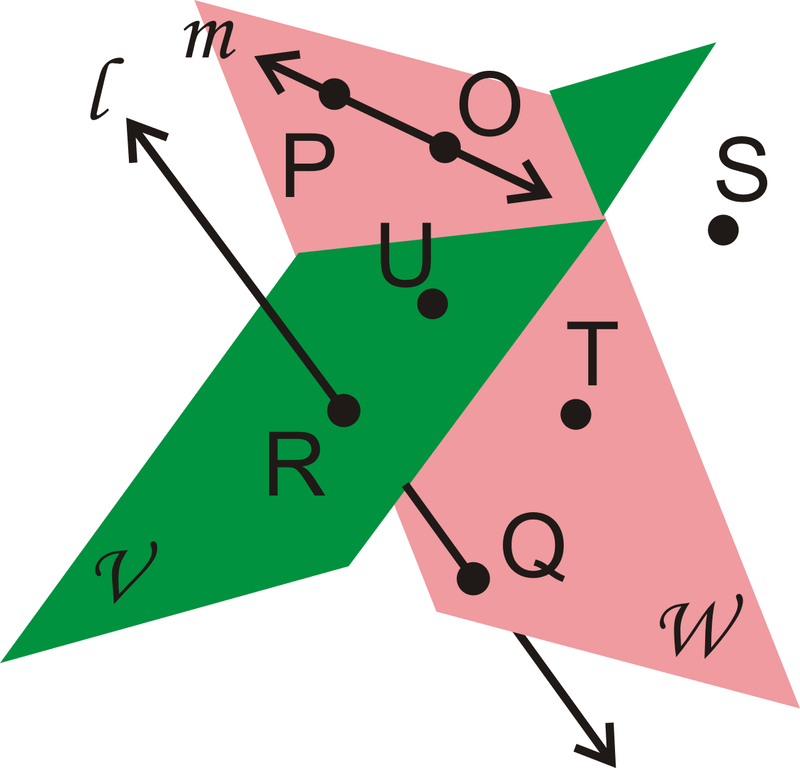
- ¿La línea es\(l\) coplanaria con Plano\(V\)\(W\), Plano, ambos o ninguno?
- ¿Son\(R\) y\(Q\) colineales?
- ¿Qué punto no pertenece ni al Plano V ni al Plano\(W\)?
- Enumere tres puntos en Plano\(W\).
Solución
- Tampoco
- Sí
- S
- Cualquier combinación de\(P\),\(O\),\(T\), y\(Q\) funcionaría.
Ejemplo\(\PageIndex{5}\)
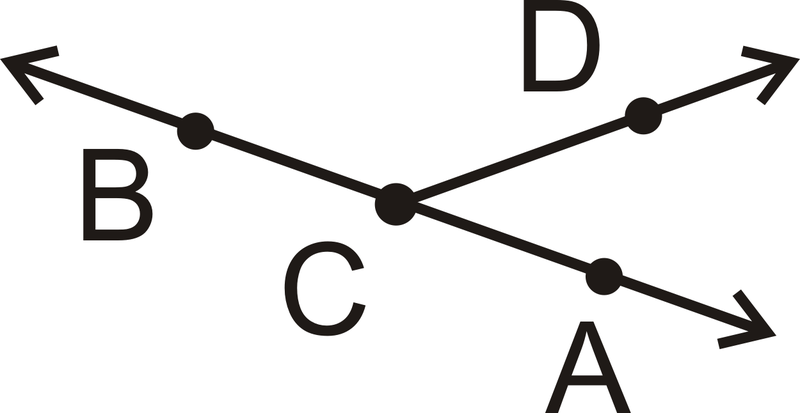
Dibuje y etiquete una figura que concuerde con la siguiente descripción: Línea\(\overleftrightarrow{AB}\) y rayo se\(\overrightarrow{CD}\) cruzan en el punto\ (C)\. Entonces, vuelve a dibujar para que la figura se vea diferente pero sigue siendo fiel a la descripción.
Solución
Ni la posición de A o B en la línea, ni la dirección que\(\overrightarrow{CD}\) apunta importan.
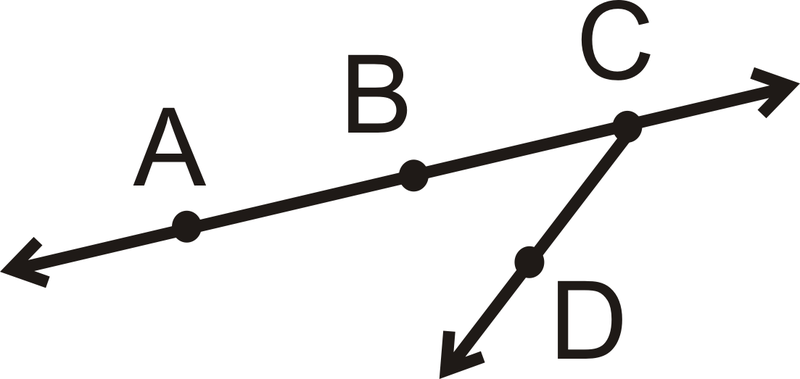
Para la segunda parte, esta es una forma de dibujar el diagrama de manera diferente:
Revisar
Para las preguntas 1-5, dibuje y etiquete una figura que se ajuste a las descripciones.
- \(\overrightarrow{CD}\)intersección\(\overline{AB}\) y Plano\(P\) que contiene\(\overline{AB}\) pero no\(\overrightarrow{CD}\).
- Tres puntos colineales\(A\),\(B\), y\(C\). \(B\)también es colineal con puntos\(D\) y\(E\).
- \(\overrightarrow{XY}\),\(\overrightarrow{XZ}\), y\(\overrightarrow{XW}\), tal que\(\overrightarrow{XY}\) y\(\overrightarrow{XZ}\) son coplanares, pero\(\overrightarrow{XW}\) no coplanares con ambos de los otros rayos.
- Dos planos que se cruzan,\(P\) y\(Q\), con\(\overline{GH}\), donde\(G\) está en plano\(P\) y\(H\) está en plano\(Q\).
- Cuatro puntos no colineales\(I\),\(J\)\(K\), y\(L\), con segmentos de línea que conectan todos los puntos entre sí.
- Nombra esta línea de cinco maneras.
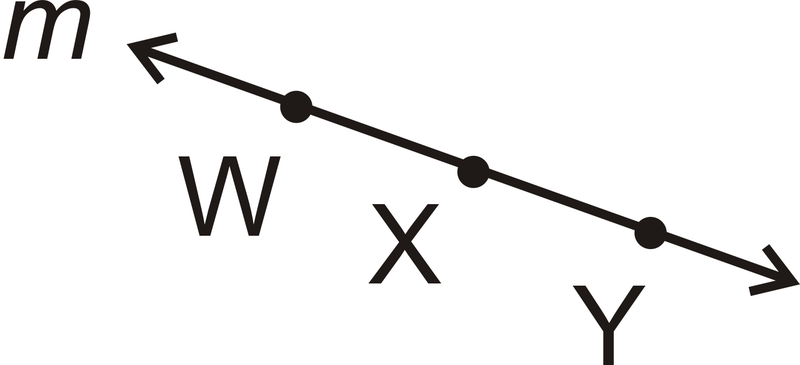
Figura\(\PageIndex{18}\)
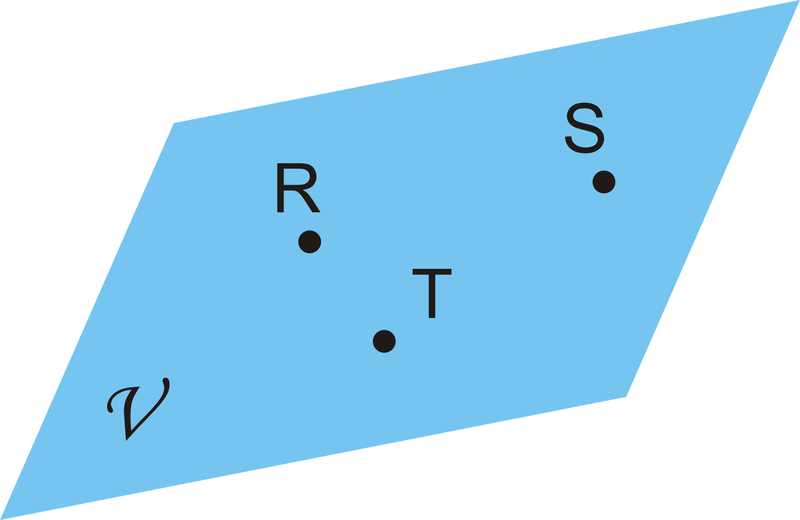
- Nombra la figura geométrica de tres formas distintas.

Figura\(\PageIndex{19}\)
- Nombra la figura geométrica de dos maneras distintas.
Figura\(\PageIndex{20}\)
- ¿Cuál es el mejor modelo geométrico posible para un campo de fútbol? Explique su respuesta.
- Enumere dos ejemplos de dónde ves rayos en la vida real.
- ¿Qué tipo de objeto geométrico es la intersección de una línea y un plano? Dibuja tu respuesta.
- ¿Cuál es la diferencia entre un postulado y un teorema?
Para 13-16, use notación geométrica para explicar cada imagen con el mayor detalle posible.
-
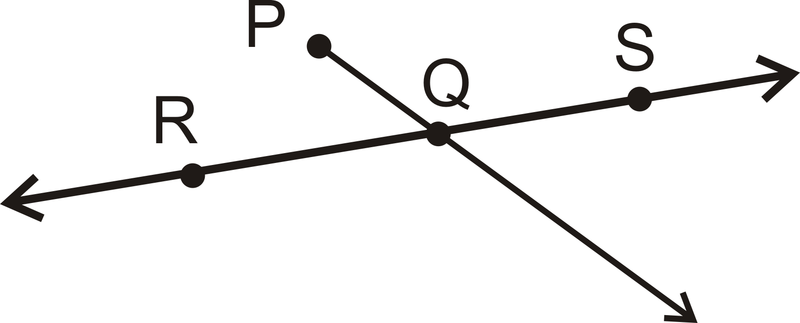
Figura\(\PageIndex{21}\) -
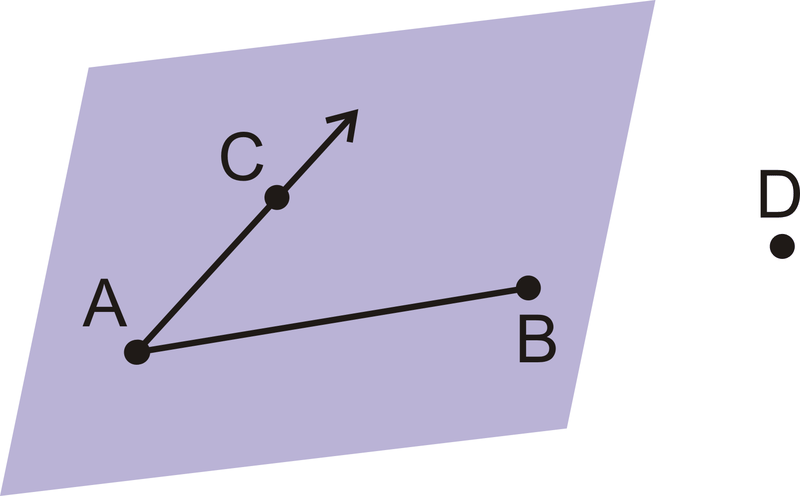
Figura\(\PageIndex{22}\) -
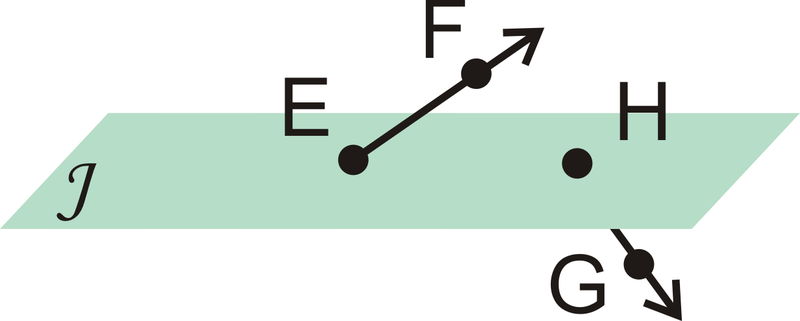
Figura\(\PageIndex{23}\)
-
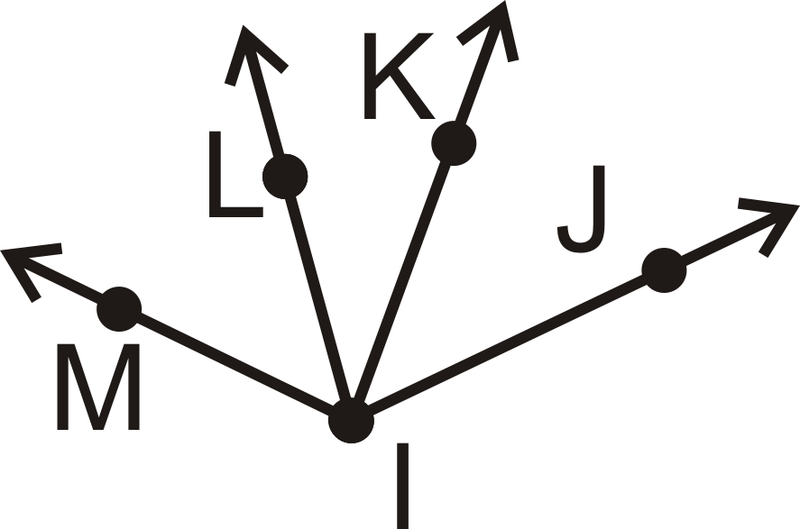
Figura\(\PageIndex{24}\)
Para 17-25, determinar si las siguientes afirmaciones son verdaderas o falsas.
- Dos puntos cualesquiera son colineales.
- Tres puntos cualesquiera determinan un plano.
- Una línea es de dos rayos con un punto final común.
- Un segmento de línea es infinitamente muchos puntos entre dos puntos finales.
- Un punto ocupa espacio.
- Una línea es unidimensional.
- Cuatro puntos cualesquiera son coplanarios.
- \(\overrightarrow{AB}\)podría leerse “rayo\(AB\)” o “rayo”\(BA\).
- \(\overleftrightarrow{AB}\)podría leerse “línea\(AB\)” o “línea”\(BA\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.1.
El vocabulario
| Término | Definición |
|---|---|
| colineales | Tres o más puntos son colineales cuando se encuentran en la misma línea. |
| coplanario | Los puntos y/o líneas ubicados en un mismo plano son coplanares. |
| punto final | Un punto final es un punto en un extremo de un segmento de línea o rayo. |
| intersección | Un punto o conjunto de puntos donde se cruzan líneas, planos, segmentos o rayos. |
| línea | Infinitamente muchos puntos que se extienden para siempre en ambas direcciones. |
| segmento de línea | Un segmento de línea es una parte de una línea que tiene dos puntos finales. |
| avión | Un plano es una superficie plana bidimensional. Se puede conceptualizar como una hoja de papel de área infinita. |
| Punto | Un punto es una ubicación en el espacio que no tiene tamaño ni forma. |
| postular | Un postulado es una afirmación que se acepta como verdadera sin pruebas. |
| ray | Una parte de una línea con un punto final que se extiende para siempre en la dirección opuesta a ese punto. |
| espacio | El espacio es el conjunto de todos los puntos que se extienden en tres dimensiones. |
| Dimensiones | Las dimensiones son las medidas que definen la forma y el tamaño de una figura. |
| No colineales | Un punto no colineal se encuentra por encima o por debajo de una línea. |
| No coplanares | Un punto no coplanar se encuentra por encima o por debajo de un plano. |
| teorema | Un teorema es una afirmación que puede demostrarse verdadera usando postulados, definiciones y otros teoremas que ya han sido probados. |
Recursos adicionales
Elemento interactivo
Video: Principios básicos de definiciones geométricas - Básicas
Actividades: Definiciones geométricas básicas Preguntas de discusión
Ayudas de estudio: Guía de estudio de conceptos básicos de geometría
Práctica: Términos de geometría
Mundo real: Definiciones geométricas básicas

