4.36: Clasificación de distancias y triángulos usando el teorema de Pitágoras

Encuentra lados faltantes para calcular el área.

Aplicaciones del Teorema de Pitágoras

Encuentra la Altura de un Triángulo Isósceles

Una forma de utilizar El Teorema de Pitágoras es encontrar la altura de un triángulo isósceles (ver Ejemplo 1).

Figura\(\PageIndex{1}\)

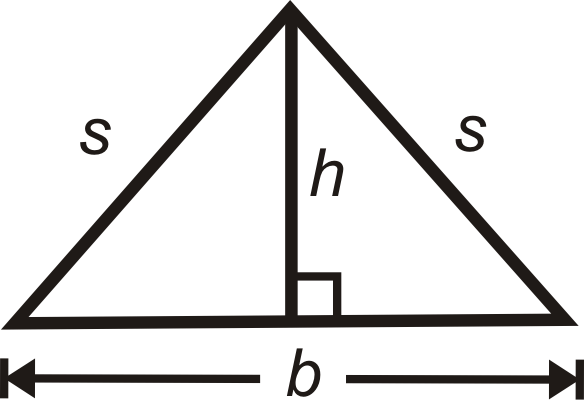
Demostrar la fórmula de distancia

Otra aplicación del Teorema de Pitágoras es la Fórmula a Distancia. Aquí lo demostraremos.

Figura\(\PageIndex{2}\)

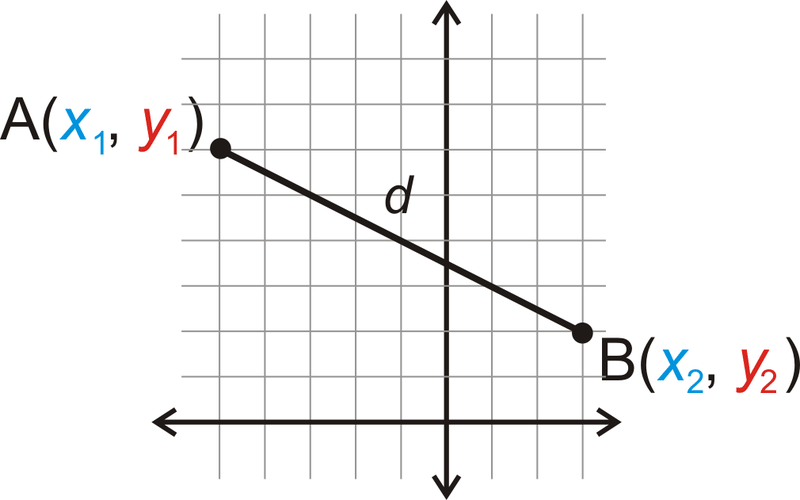
Empecemos con punto\(A(x_1,y_1)\) y punto\(B(x_2, y_2)\). Llamaremos a la distancia entre\(A\) y\(B\),\(d\).

Dibuja las longitudes vertical y horizontal para hacer un triángulo rectángulo.

Figura\(\PageIndex{3}\)

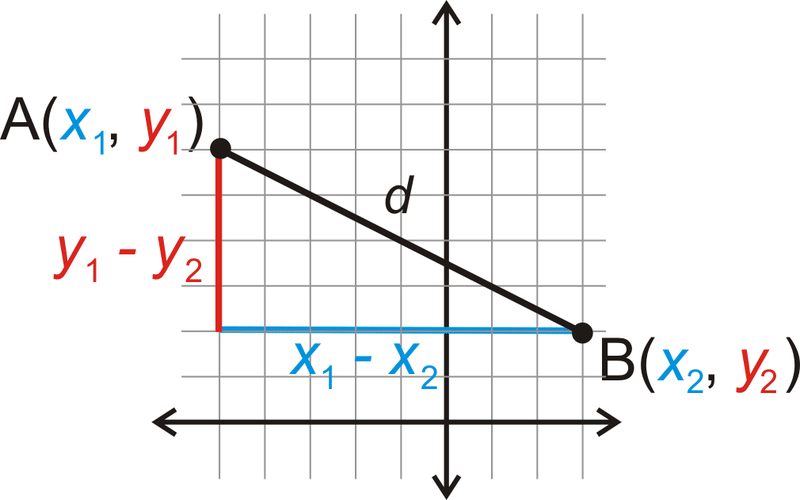
Ahora que tenemos un triángulo rectángulo, podemos usar el Teorema de Pitágoras para encontrar la hipotenusa,\(d\).

\(\begin{align*} d^2=(x_1−x_2)^2+(y_1−y_2)^2 \\ d=\sqrt{(x_1−x_2)^2+(y_1−y_2)^2} \end{align*} \)

Fórmula de distancia: La distancia entre\(A(x_1, y_1)\) y\(B(x_2, y_2)\) es\(d=\sqrt{(x_1−x_2)^2+(y_1−y_2)^2}\).

Clasificar un triángulo como agudo, derecho u obtuso

Podemos extender lo contrario del Teorema de Pitágoras para determinar si un triángulo es un triángulo obtuso o agudo.

Triángulos Agudos: Si la suma de los cuadrados de los dos lados más cortos en un triángulo rectángulo es mayor que el cuadrado del lado más largo, entonces el triángulo es agudo.

Figura\(\PageIndex{4}\)

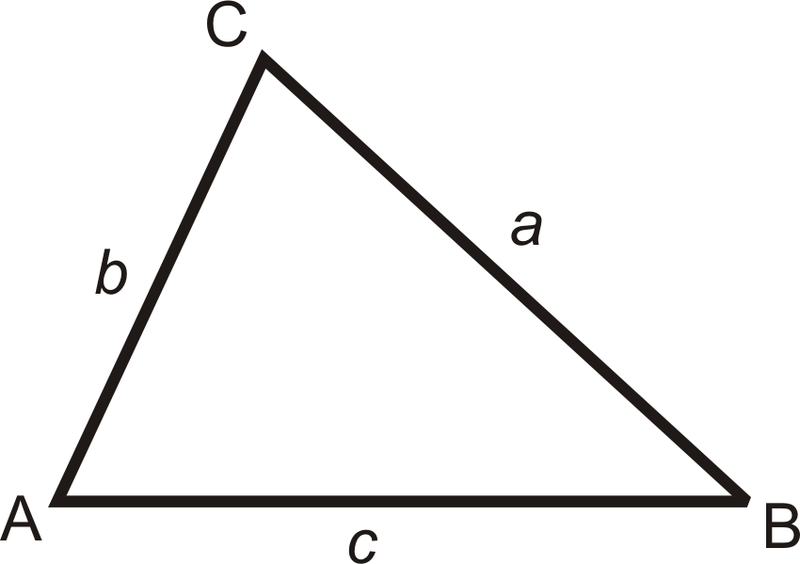
Para\(b<c\) y\(a<c\), si\(a^2+b^2>c^2\), entonces el triángulo es agudo.

Triángulos obtusos: Si la suma de los cuadrados de los dos lados más cortos en un triángulo rectángulo es menor que el cuadrado del lado más largo, entonces el triángulo es obtuso.

Figura\(\PageIndex{5}\)

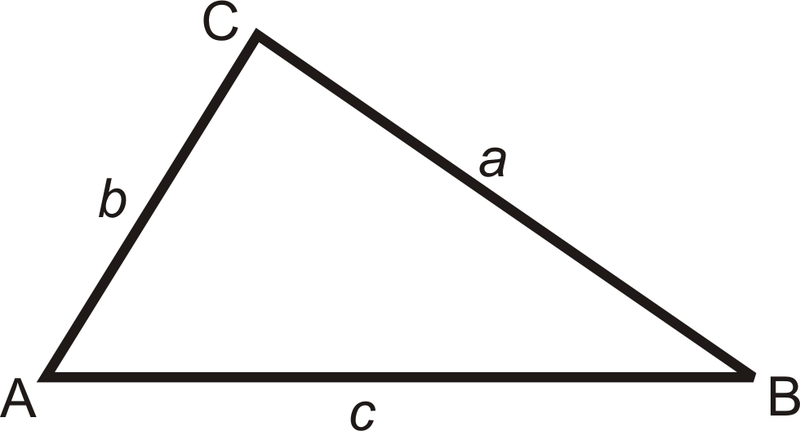
Para\(b<c\) y\(a<c\), si\(a^2+b^2<c^2\), entonces el triángulo es obtuso.

¿Y si te dieran un triángulo equilátero en el que todos los lados midieran 4 pulgadas? ¿Cómo podrías usar el Teorema de Pitágoras para encontrar la altitud del triángulo?

Ejemplo\(\PageIndex{1}\)

¿Cuál es la altura del triángulo isósceles?

Figura\(\PageIndex{6}\)

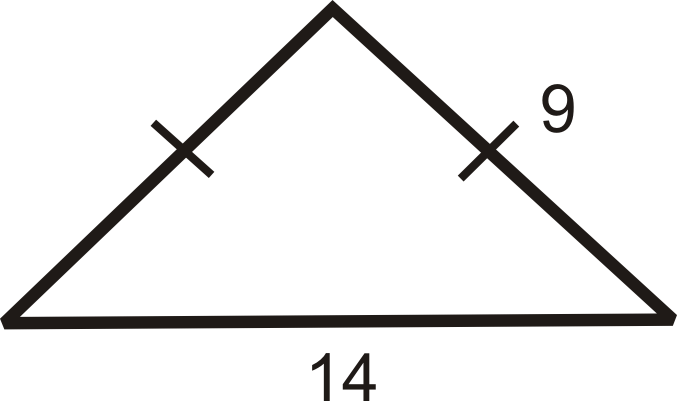
Solución

Dibuja la altitud desde el vértice entre los lados congruentes, que biseccionará la base.

Figura\(\PageIndex{7}\)

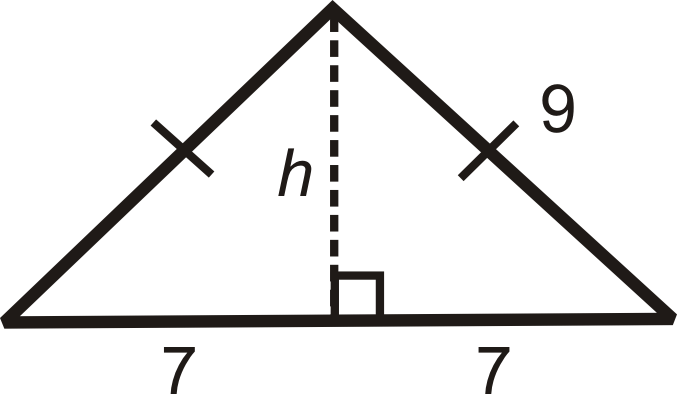
\(\begin{align*} 7^2+h^2&=9^2 \\ 49+h^2&=81 \\ h^2&=32 \\ h&=\sqrt{32}=\sqrt{16\cdot 2}=4\sqrt{2}\end{align*}\)

Ejemplo\(\PageIndex{2}\)

Encuentra la distancia entre\((1, 5)\) y\((5, 2)\).

Solución

Hacer\(A(1,5)\) y\(B(5,2)\). Enchufe en la fórmula de distancia.

\(\begin{align*} d &=\sqrt{(1−5)^2+(5−2)^2} \\ &=\sqrt{(−4)^2+(3)^2} \\ &=\sqrt{16+9}=\sqrt{25}=5\end{align*}\)

Al igual que las longitudes de los lados de un triángulo, las distancias son siempre positivas.

Ejemplo\(\PageIndex{3}\)

Gráfica\(A(−4,1)\),\(B(3,8)\), y\(C(9,6)\). Determinar si\(\Delta{ABC}\) es agudo, obtuso o correcto.

Figura\(\PageIndex{8}\)

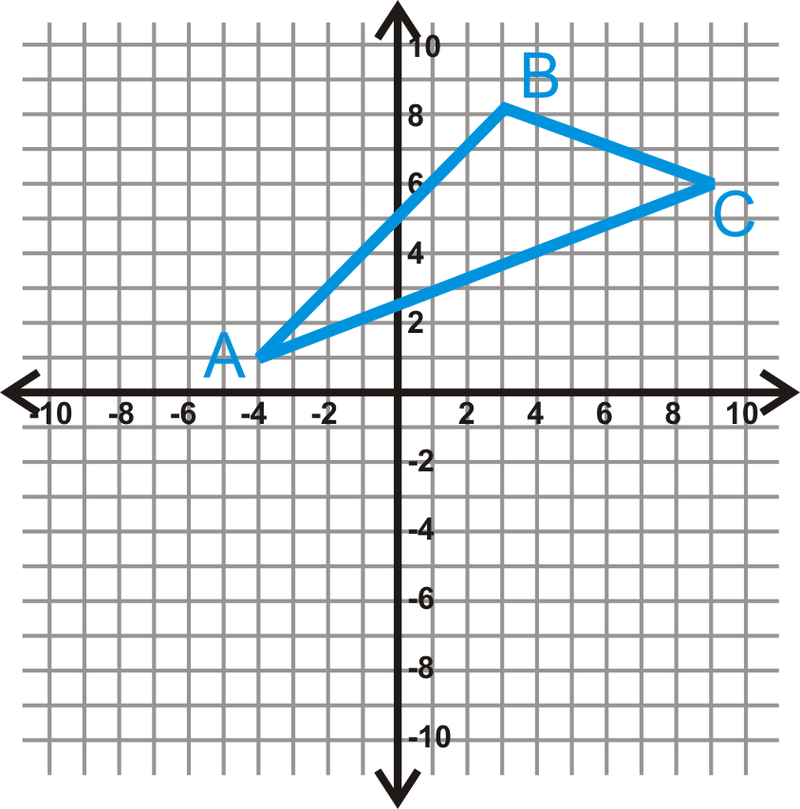
Solución

Usa la fórmula de distancia para encontrar la longitud de cada lado.

\(\begin{align*} AB&=\sqrt{(−4−3)^2+(1−8)^2}=\sqrt{49+49}=\sqrt{98} \\ BC &=\sqrt{(3−9)^2+(8−6)^2}=\sqrt{36+4}=\sqrt{40} \\ AC &=\sqrt{(−4−9)^2+(1−6)^2}=\sqrt{169+25}=\sqrt{194}\end{align*}\)

Enchufe estas longitudes en el Teorema de Pitágoras.

\(\begin{align*} \sqrt{98})^2+(\sqrt{40})^2 &? (\sqrt{194})^2 \\ 98+40 &? 194 \\ 138 &< 194\end{align*}\)

\(\Delta{ABC}\)es un triángulo obtuso.

Para los Ejemplos 4 y 5, determinar si los triángulos son agudos, derechos u obtusos.

Ejemplo\(\PageIndex{4}\)

Establezca el lado más largo en c.

Figura\(\PageIndex{9}\)

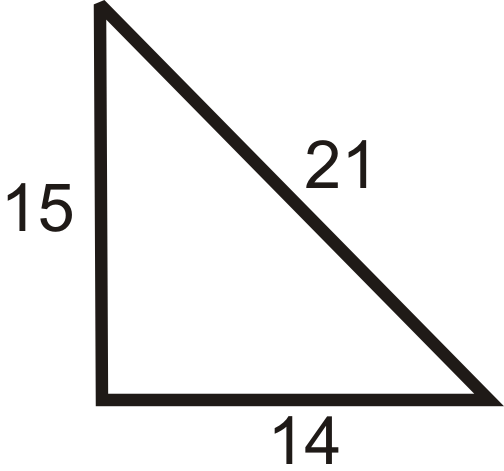
Solución

\(\begin{align*} 15^2+14^2 &? \: 21^2 \\ 225+196 &? \: 441 \\ 421 &< 441\end{align*}\)

El triángulo es obtuso.

Ejemplo\(\PageIndex{5}\)

Establecer el lado más largo a\(c\).

Solución

Un triángulo con longitudes laterales 5, 12, 13.

\(5^2+12^2=13^2\)entonces este triángulo está a la derecha.

Revisar

Encuentra la altura de cada triángulo isósceles a continuación. Simplifica todos los radicales.

1. 

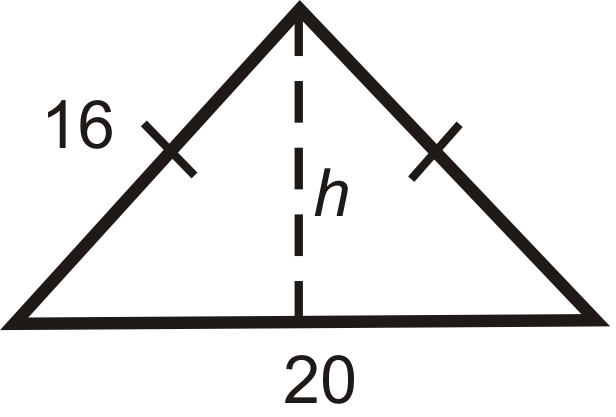
   Figura\(\PageIndex{10}\)

2. 

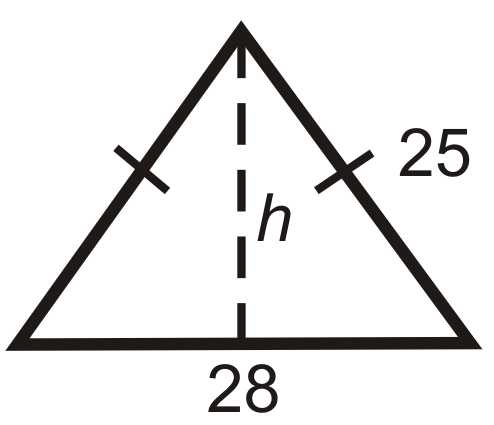
   Figura\(\PageIndex{11}\)

3. 

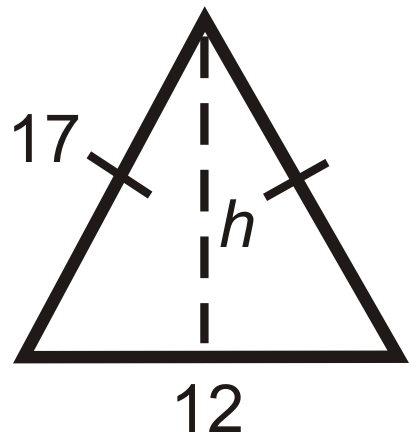
   Figura\(\PageIndex{12}\)

Encuentra la longitud entre cada par de puntos.

4. \((-1, 6)\)y\((7, 2)\)
5. \((10, -3)\)y\((-12, -6)\)
6. \((1, 3)\)y\((-8, 16)\)
7. ¿Cuál es el largo y ancho de un HDTV de 42”? Redondea tu respuesta a la décima más cercana.
8. Los televisores de definición estándar tienen una relación de longitud y ancho de 4:3. ¿Cuál es el largo y ancho de un televisor de definición estándar de 42”? Redondea tu respuesta a la décima más cercana.

Determinar si los siguientes triángulos son agudos, derechos u obtusos.

9. 7, 8, 9
10. 14, 48, 50
11. 5, 12, 15
12. 13, 84, 85
13. 20, 24
14. 35, 40, 51
15. 39, 80, 89
16. 20, 21, 38
17. 48, 55, 76

Grafica cada conjunto de puntos y determina si\ Delta {ABC} es agudo, derecho u obtuso, usando la fórmula de distancia.

18. \(A(3,−5), B(−5,−8), C(−2,7)\)
19. \(A(5,3), B(2,−7), C(−1,5)\)
20. \(A(1,6), B(5,2), C(−2,3)\)
21. \(A(−6,1), B(−4,−5), C(5,−2)\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.3.

Recursos

vocabulario

Término	Definición
triángulo agudo	Un triángulo donde todos los ángulos son menores a 90°.
Triángulo Obtuso	Un triángulo obtuso es un triángulo con un ángulo que es mayor a 90 grados.
Fórmula de distancia	La distancia entre dos puntos\((x_1,y_1)\) y se\((x_2, y_2)\) puede definir como\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\).
Teorema de Pitágoras	El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo.
Vertex	Un vértice es un punto de intersección de las líneas o rayos que forman un ángulo.

Recursos adicionales

Elemento Interactivo

Video: El teorema de Pitágoras y Lo Converso del Teorema de Pitágoras

Actividades: Aplicaciones del Teorema de Pitágoras Preguntas de Discusión

Práctica: Clasificación de distancias y triángulos usando el teorema de Pitágoras