7.10: Triángulos proporcionales
- Page ID
- 107443
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lados divididos por una línea paralela al tercer lado de un triángulo.
Teorema de la proporcionalidad del triángulo
Piensa en un segmento medio de un triángulo. Un segmento medio es paralelo a un lado de un triángulo y divide los otros dos lados en mitades congruentes. El segmento medio divide esos dos lados proporcionalmente. Pero ¿qué pasa con otra línea que es paralela, pero que no divide los otros dos lados en mitades congruentes? De hecho, tal línea seguirá dividiendo los lados proporcionalmente. A esto se le llama Teorema de la proporcionalidad del triángulo.
Teorema de la proporcionalidad del triángulo: Si una línea paralela a un lado de un triángulo se cruza con los otros dos lados, entonces divide esos lados proporcionalmente.
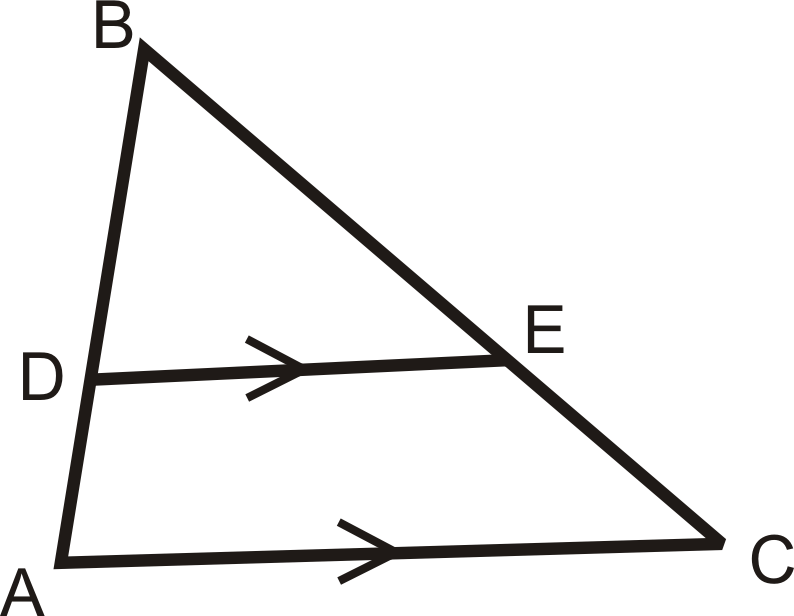
Si\(\overline{DE}\parallel \overline{AC}\), entonces\(\dfrac{BD}{DA}=\dfrac{BE}{EC}\). (\(\dfrac{DA}{BD}=\dfrac{EC}{BE}\)es también una verdadera proporción. )
Lo contrario de este teorema también es cierto.
Teorema de la proporcionalidad del triángulo Converse: Si una línea divide proporcionalmente dos lados de un triángulo, entonces es paralela al tercer lado.
Si\(\dfrac{BD}{DA}=\dfrac{BE}{EC}\), entonces\(\overline{DE}\parallel \overline{AC}\).
¿Y si te dieran un triángulo con un segmento de línea dibujado a través de él de un lado a otro? ¿Cómo podría usar la información sobre las longitudes de los lados del triángulo para determinar si ese segmento de línea es paralelo al tercer lado?
Usa el diagrama para responder Ejemplos 1 y 2. \(\overline{DB}\parallel \overline{FE}\).
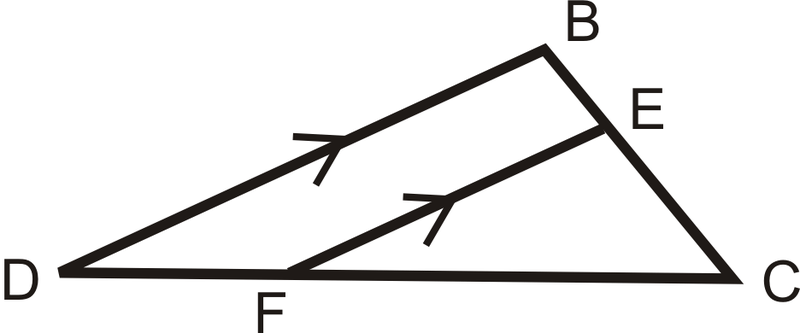
Ejemplo\(\PageIndex{1}\)
Nombra los triángulos similares. Escribe la declaración de similitud.
Solución
\(\Delta DBC\sim \Delta FEC\)
Ejemplo\(\PageIndex{2}\)
\(\dfrac{FC+?}{FC}=\dfrac{?}{FE}\)
Solución
\(DF\);\(DB\)
Ejemplo\(\PageIndex{3}\)
A continuación se dibuja un triángulo con su segmento medio. ¿Cuál es la relación en la que el segmento medio divide los lados?
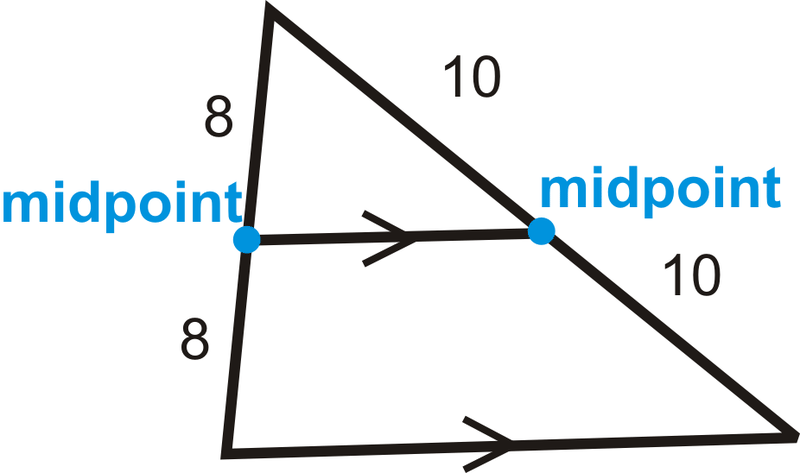
Solución
El segmento medio divide los lados de manera uniforme. La relación sería 8:8 o 10:10, que ambos reducen a 1:1.
Ejemplo\(\PageIndex{4}\)
En el diagrama a continuación,\(\overline{EB}\parallel \overline{CD}\). Encuentra\(BC\).
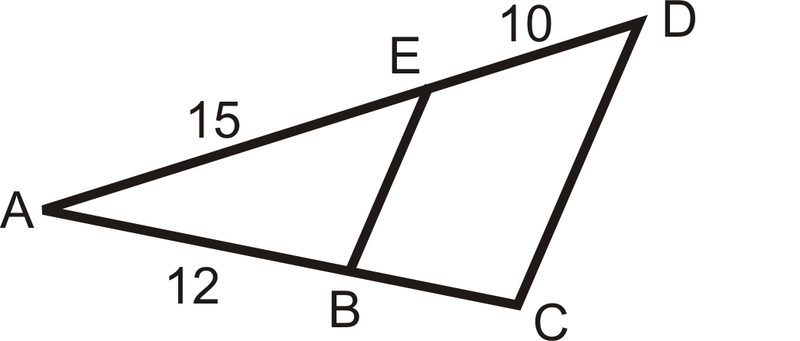
Solución
Para resolver, establecer una proporción.
\(\begin{aligned} \dfrac{10}{15}=\dfrac{BC}{12} \rightarrow 15(BC)&=120 \\ BC&=8 \end{aligned}\)
Ejemplo\(\PageIndex{5}\)
¿Es\(\overline{DE}\parallel \overline{CB}\)?
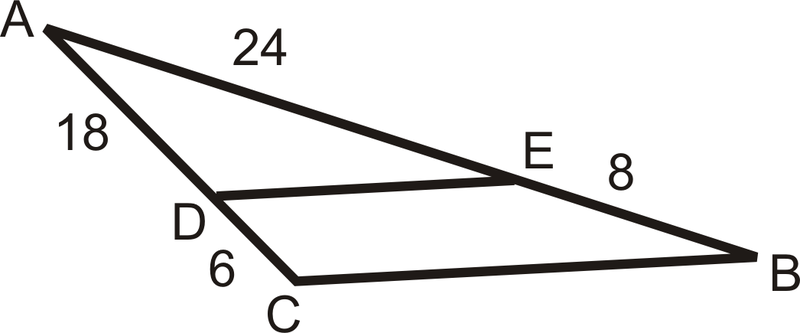
Solución
Si las relaciones son iguales, entonces las líneas son paralelas.
\(\dfrac{6}{18}=\dfrac{8}{24}=\dfrac{1}{3}\)
Debido a que las proporciones son iguales,\(\overline{DE}\parallel \overline{CB}\).
Revisar
Utilice el diagrama para responder a las preguntas 1-7. \(\overline{AB}\parallel \overline{DE}\).
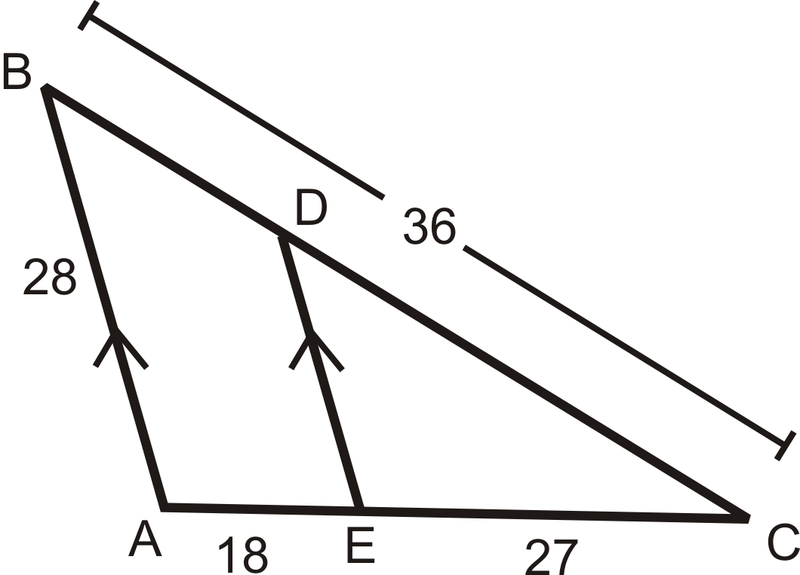
- Encuentra\(BD\).
- Encuentra\(DC\).
- Encuentra\(DE\).
- Encuentra\(AC\).
- ¿Qué es\(BD:DC\)?
- ¿Qué es\(DC:BC\)?
- ¿Por qué\(BD:DC\neq DC:BC\)?
Utilice las longitudes dadas para determinar si\(\overline{AB}\parallel \overline{DE}\).
-
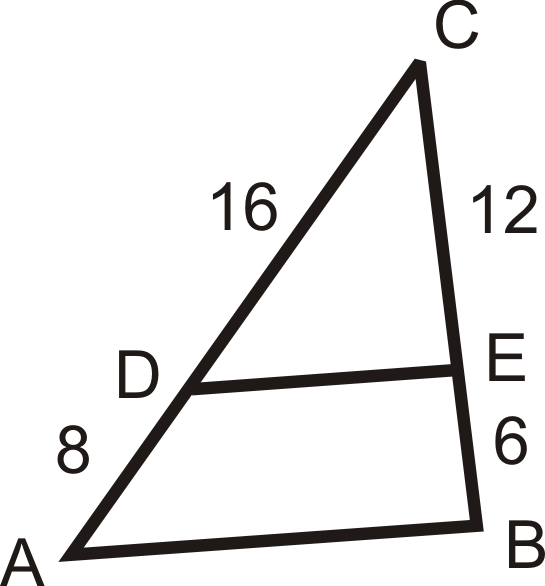
Figura\(\PageIndex{7}\) -
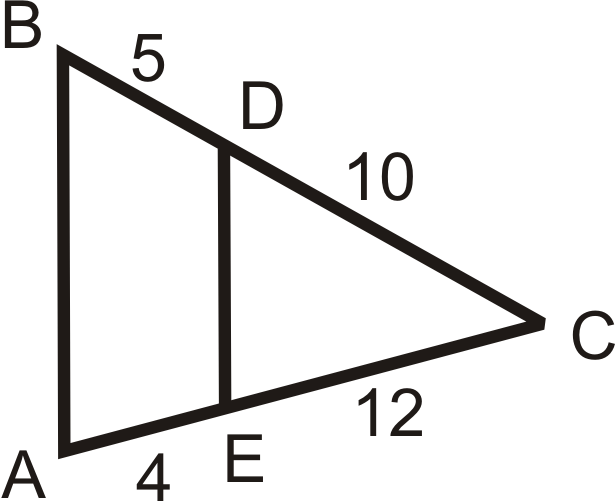
Figura\(\PageIndex{8}\) -
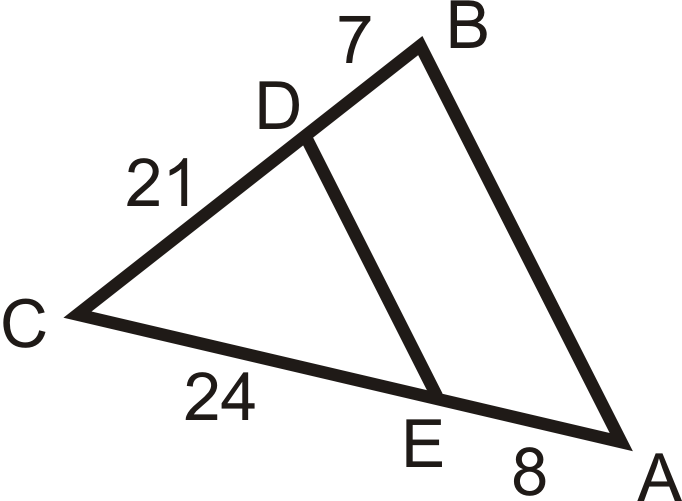
Figura\(\PageIndex{9}\) -
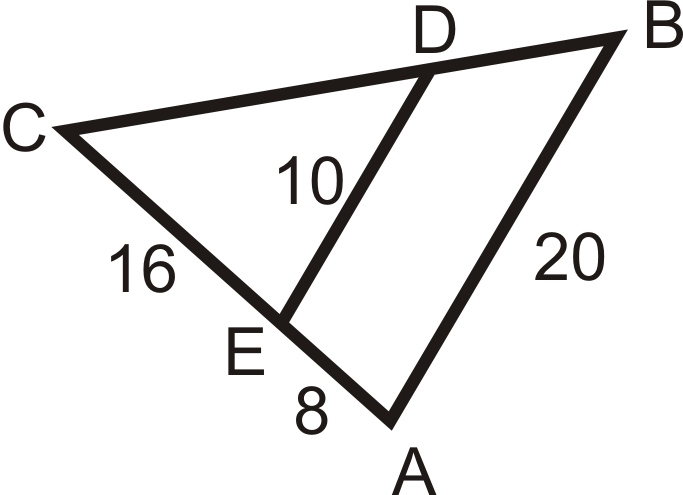
Figura\(\PageIndex{10}\) -
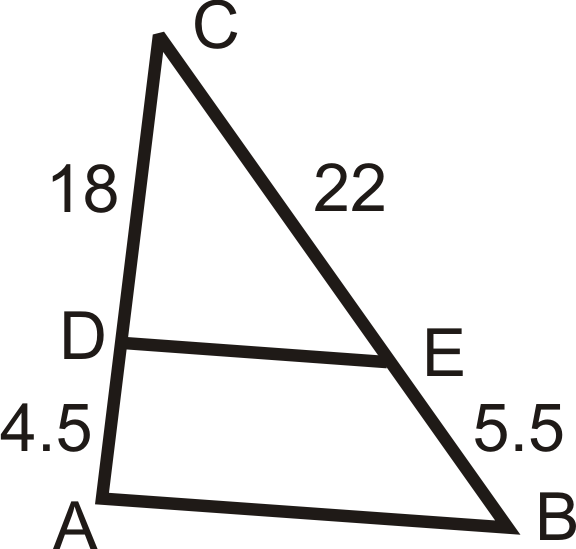
Figura\(\PageIndex{11}\) -
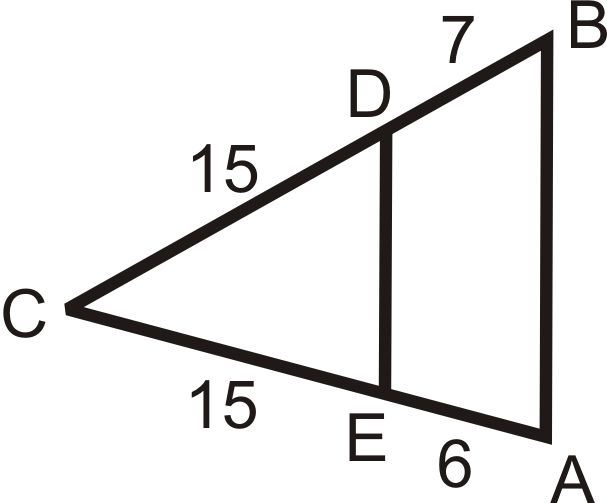
Figura\(\PageIndex{12}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.8.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| segmento medio | Un segmento medio conecta los puntos medios de dos lados de un triángulo o los lados no paralelos de un trapecio. |
| Paralelo | Dos o más líneas son paralelas cuando se encuentran en el mismo plano y nunca se cruzan. Estas líneas siempre tendrán la misma pendiente. |
| Proporción | Una proporción es una ecuación que muestra dos proporciones equivalentes. |
| Teorema de la proporcionalidad del triángulo | El Teorema de Proporcionalidad Triangular establece que si una línea es paralela a un lado de un triángulo e intersecta los otros dos lados, entonces divide esos lados proporcionalmente. |
| Teorema de proporcionalidad de triángulo Converse | El teorema de proporcionalidad del triángulo converse establece que si una línea divide proporcionalmente dos lados de un triángulo, entonces es paralela al tercer lado. |
Recursos adicionales
Video: Uso de las propiedades del teorema de proporcionalidad triangular para resolver valores desconocidos
Actividades: Preguntas de discusión sobre la proporcionalidad del triángulo
Ayudas de estudio: Guía de estudio de relaciones de proporcionalidad
Práctica: Triángulos proporcionales
Mundo real: proporcionalidad triangular