11.1 Teorema Fundamental de Álgebra
- Page ID
- 107257
Has aprendido que un cuadrático tiene como máximo dos ceros reales y un cúbico tiene como máximo tres ceros reales. Es posible que hayas notado que el número de ceros reales siempre es menor o igual al grado del polinomio. Al mirar una gráfica se puede ver cuando una parábola cruza el\(x\) eje 0,1 o 2 veces, pero ¿qué tiene que ver esto con números complejos?
El teorema fundamental del álgebra
Un número real es cualquier número racional o irracional. Cuando un número real es cuadrado, siempre producirá un valor no negativo. Los números complejos incluyen números reales y otro tipo de número llamado números imaginarios. A diferencia de los números reales, los números imaginarios pueden producir un valor negativo al cuadrado. La raíz cuadrada del negativo se define como el número imaginario\(i\).
\(i=\sqrt{-1}\)y\(i^{2}=-1\)
Los números complejos se escriben con un componente real y un componente imaginario. Todos los números complejos se pueden escribir en la forma\(a+b i\). Cuando el componente imaginario es cero, el número es simplemente un número real. Esto significa que los números reales son un subconjunto de números complejos.
El Teorema Fundamental del Álgebra afirma que un polinomio de\(n^{t h}\) grado con coeficientes reales o complejos tiene, con multiplicidad, raíces exactamente\(n\) complejas. Esto significa que un cúbico tendrá exactamente 3 raíces, algunas de las cuales pueden ser complejas.
Toma el siguiente polinomio.
\(f(x)=x^{2}+9\)
Al principio se puede pensar que esto no tiene ninguna raíz pero el Teorema Fundamental del Álgebra establece que debe tener 2 raíces. Ambas raíces para este polinomio son complejas.
Para encontrar las raíces de este complejo polinomio, establecer\(y=0\) y resolver para\(x\). Esto te dará los dos ceros.
\(\begin{aligned} 0 &=x^{2}+9\\-9 &=x^{2} \\ \pm 3 i &=x \end{aligned}\)
Así, la factorización lineal de la función es:
\(f(x)=(x-3 i)(x+3 i)\)
Multiplicidad se refiere a cuando una raíz cuenta más de una vez. Por ejemplo, en la siguiente función la única raíz ocurre en\(x=3\).
\(f(x)=(x-3)^{2}\)
El Teorema Fundamental del Álgebra establece que este\(2^{\text {nd }}\) grado polinomio debe tener exactamente 2 raíces con multiplicidad. Esto quiere decir que la raíz\(x=3\) tiene multiplicidad 2. Una manera de determinar la multiplicidad es simplemente mirar el grado de cada uno de los factores en el polinomio factorizado.
\(g(x)=(x-1)(x-3)^{4}(x+2)\)
Esta función tiene 6 raíces. Las dos primeras raíces\(x=1\) y\(x=-2\) tienen multiplicidades de 1 porque el poder de cada uno de sus factores binomiales es 1. La tercera raíz\(x=3\) tiene una multiplicidad de 4 porque la potencia de su factor binomial es 4. Tenga en cuenta que todos los polinomios se pueden escribir en forma factorizada como el polinomio anterior, debido a un teorema llamado Teorema de Factorización Lineal.
Ejemplos
Anteriormente, se le preguntó sobre las gráficas de las parábolas y sus relaciones con los ceros de las parábolas. Cuando una parábola no logra cruzar el\(x\) eje todavía tiene 2 raíces. Estas dos raíces resultan ser números imaginarios. La función\(f(x)=x^{2}+4\) no cruza el\(x\) eje, sino que sus raíces lo son\(x=\pm 2 i\).
Identificar el polinomio que tiene las siguientes cinco raíces. \(x=0,2,3, \pm \sqrt{5} i\)
Escribe la función en forma factorizada.
\(f(x)=(x-0)(x-2)(x-3)(x-\sqrt{5} i)(x+\sqrt{5} i)\)
Cuando se multiplica, será útil hacer primero los conjugados complejos. Recuerde que los conjugados complejos son pares de números complejos con partes reales que son idénticas y partes imaginarias que son de igual magnitud pero signos opuestos. Los conjugados complejos en esta ecuación son\((x-\sqrt{5} i)(x+\sqrt{5} i)\).
\(f(x)=x\left(x^{2}-5 x+6\right)\left(x^{2}-5 \cdot(-1)\right)\)
\(f(x)=\left(x^{3}-5 x^{2}+6 x\right)\left(x^{2}+5\right)\)
\(f(x)=x^{5}-5 x^{4}+6 x^{3}+5 x^{3}-25 x^{2}+30 x\)
\(f(x)=x^{5}-5 x^{4}+11 x^{3}-25 x^{2}+30 x\)
Escribe el polinomio que tiene las siguientes raíces: 4 (con multiplicidad 3), 2 (con multiplicidad 2) y 0.
\(f(x)=(x-4)^{3} \cdot(x-2)^{2} \cdot x\)
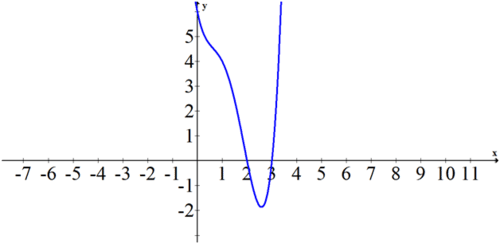
Factorizar el siguiente polinomio en su factorización lineal y declarar todas sus raíces.
\(f(x)=x^{4}-5 x^{3}+7 x^{2}-5 x+6\)
Se puede utilizar la división polinómica larga para obtener la siguiente factorización.
\(f(x)=(x-3)(x-2)(x-i)(x+i)\)
Si necesitas un lugar para comenzar, es útil mirar la gráfica del polinomio y notar que la gráfica te muestra exactamente dónde aparecen las raíces reales.
¿Se puede crear un polinomio con coeficientes reales que tenga una raíz imaginaria? ¿Por qué o por qué no?
No, si un polinomio tiene coeficientes reales entonces o no tiene raíces imaginarias, o las raíces imaginarias vienen en pares de conjugados complejos (de manera que las porciones imaginarias se cancelan cuando se multiplican los factores).
Para\(1-4,\) encontrar el polinomio con las raíces dadas.
1.2 (con multiplicidad 2), 4 (con multiplicidad 3),\(1, \sqrt{2} i,-\sqrt{2} i\).
2. 1, -3 (con multiplicidad 3),\(-1, \sqrt{3} i,-\sqrt{3} i\)
3. 5 (con multiplicidad 2), -1 (con multiplicidad 2),\(2 i,-2 i\)
4. \(i,-i, \sqrt{2} i,-\sqrt{2} i\)
Para cada polinomio, factorizar en su factorización lineal y declarar todas sus raíces.
5. \(f(x)=x^{5}+4 x^{4}-2 x^{3}-14 x^{2}-3 x-18\)
6. \(g(x)=x^{4}-1\)
7. \(h(x)=x^{6}-12 x^{5}+61 x^{4}-204 x^{3}+532 x^{2}-864 x+576\)
8. \(j(x)=x^{7}-11 x^{6}+49 x^{5}-123 x^{4}+219 x^{3}-297 x^{2}+243 x-81\)
9. \(k(x)=x^{5}+3 x^{4}-11 x^{3}-15 x^{2}+46 x-24\)
10. \(m(x)=x^{6}-12 x^{4}+23 x^{2}+36\)
11. \(n(x)=x^{6}-3 x^{5}-10 x^{4}-32 x^{3}-81 x^{2}-85 x-30\)
12. \(p(x)=x^{6}+4 x^{5}+7 x^{4}+12 x^{3}-16 x^{2}-112 x-112\)
13. ¿Cómo se puede saber el número de raíces que tiene un polinomio a partir de su ecuación?
14. Explicar el significado del término “multiplicidad”.
15. Un polinomio con coeficientes reales tiene una raíz que es\(\sqrt{3} i\). ¿Qué otra raíz (s) debe tener el polinomio?