1.2: Conversación del Teorema de Pitágoras
- Page ID
- 107697
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar triángulos rectos usando el teorema
Derivar y Usar la Conversación del Teorema de Pitágoras

Brandon acaba de comprar su primera casa y está muy ansioso por plantar un jardín de flores en una sección triangular del patio trasero. Brandon ha heredado una cerca metálica que su abuelo había hecho hace muchos años y le gustaría usarla en su jardín. La barda consta de dos piezas que se sueldan entre sí para formar una pieza recta en ángulo recto y otra larga recta. Sabe que las piezas de barda cabrán en el jardín si su jardín triangular es un triángulo rectángulo.
“Si tan solo pudiera usar las medidas del jardín de 29 pies, 20 pies y 29 pies para averiguar si mi espacio de jardín forma un triángulo rectángulo, entonces podría usar la cerca del abuelo”, pensó para sí mismo.
En este concepto, aprenderás a derivar y utilizar lo contrario del Teorema de Pitágoras.
El Converso del Teorema de Pitágoras
El Teorema de Pitágoras establece que para un triángulo rectángulo el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Este teorema puede ser modelado por la ecuación\(c^2=a^2+b^2\) donde '\(c\)' representa la longitud de la hipotenusa, 'a' representa la longitud de una pata y 'b' representa la longitud de la otra pierna.
El Teorema de Pitágoras se puede utilizar para calcular la longitud de un lado desconocido de un triángulo rectángulo. El Converse del Teorema de Pitágoras establece que si el cuadrado de la longitud de un lado de un triángulo es igual a la suma de los cuadrados de las longitudes de los otros dos lados, entonces el ángulo opuesto al lado más largo es un ángulo recto. Un triángulo que contiene un ángulo recto es un triángulo rectángulo.
Veamos lo contrario del Teorema de Pitágoras en acción.
Determine si los siguientes triángulos (que pueden no ser dibujados a escala) son o no triángulos rectos. Si el triángulo es un triángulo rectángulo, realice los cambios necesarios en el triángulo y dibuje correctamente.
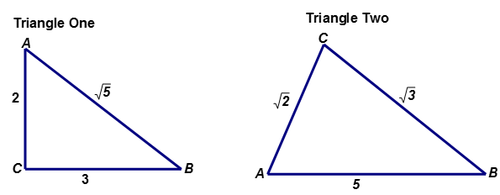
Empecemos por el Triángulo Uno.
Primero, determinar el lado más largo del triángulo.
Las longitudes de los lados son 2, 3 y\(\sqrt{5}\). La longitud del lado\(BC\) es\(\sqrt{5}\approx 2.24 \text{ units}\). El lado más largo del triángulo es el\(AB\) que será la hipotenusa del triángulo si\(\Delta ABC\) es un triángulo rectángulo.
A continuación, sustituya los valores\((2,\sqrt{5},3)\) para\((a,b,c) \) respectivamente en la ecuación c^2=a^2+b^2.
c^2&=a^2+b^2\\ (3) ^2&= (2) ^2+ (\ sqrt {5}) ^2
A continuación, cuadrar cada uno de los términos indicados en la ecuación.
\(\begin{aligned} (3)^2&=(2)^2+(\sqrt{5})^2 \\ (3\times 3)&=(2 \times 2)+(\sqrt{5}\times \sqrt{5})\end{aligned}\)
A continuación, evalúe cada una de las casillas.
\(\begin{aligned} (3\times 3)&=(2\times 2)+(\sqrt{5} \times \sqrt{5}) \\ 9&=4+5 \end{aligned}\)
Después, simplifique el lado derecho de la ecuación sumando los números.
\(\begin{aligned} 9&=4+5 \\ 9&=9 \end{aligned}\)
Ambos lados de la ecuación son iguales. El cuadrado de la longitud de un lado del triángulo es igual a la suma de los cuadrados de las longitudes de los otros dos lados. El Triángulo Uno es un triángulo rectángulo. La longitud de\(BC\) debe ser 3 y la longitud de\(AB\) debe ser\(\sqrt{5}\) ya que el ángulo recto se encuentra en\(C\).
Veamos el Triángulo Dos.
Primero, determinar el lado más largo del triángulo.
Las longitudes de los lados son\(\sqrt{2}\),\(\sqrt{3}\) y 5. La longitud del lado\(AC\) es\(\sqrt{2}\), aproximadamente 1.41 unidades de longitud. La longitud del lado BC es\(\sqrt{3}\), aproximadamente 1.73 unidades de longitud. El lado más largo del triángulo es AB que será la hipotenusa del triángulo si\(\Delta ABC\) es un triángulo rectángulo.
A continuación, sustituya los valores\((\sqrt{2},\sqrt{3},5)\) para\((a,b,c)\) respectivamente en la ecuación\(c^2=a^2+b^2\).
\ (\ begin {alineado} c^2&=a^2+b^2\\ (5) 2&= (\ sqrt {2}) ^2+ (\ sqrt {3}) ^2\ end {alineado}、)
A continuación, cuadrar cada uno de los términos indicados en la ecuación.
\(\begin{aligned} (5)^2&=(\sqrt{2})^2+(\sqrt{3})^2 \\ (5\times 5)&=(\sqrt{2}\times \sqrt{2})+(\sqrt{3}\times \sqrt{3})\end{aligned}\)
A continuación, evalúe cada una de las casillas.
\(\begin{aligned} (5\times 5)&=(\sqrt{2}\times \sqrt{2})+(\sqrt{3}\times \sqrt{3}) \\ 25&=2+3 \end{aligned}\)
Después, simplifique el lado derecho de la ecuación sumando los números.
\(\begin{aligned}25&=2+3 \\ 25&\neq 5\end{aligned}\)
Ambos lados de la ecuación no son iguales. El cuadrado de la longitud de un lado del triángulo NO es igual a la suma de los cuadrados de las longitudes de los otros dos lados. El Triángulo Dos no es un triángulo rectángulo.
Antes, te dieron un problema sobre el jardín de flores de Brandon y su cerca metálica. Necesita averiguar si su espacio de jardín es un triángulo rectángulo. ¿Cómo puede Brandon resolver esto usando las medidas del espacio?
Solución
Primero, determinar los valores para (a, b, c) de un triángulo rectángulo utilizando las medidas de 29, 20 y 21 pies.
El lado más largo representará '\(c\)' la hipotenusa.
\(\begin{aligned} a&=20 \\ b&=21 \\ c&=29 \end{aligned}\)
A continuación, sustituir los valores dados en el Teorema de Pitágoras.
\(\begin{aligned} c^2=a^2+b^2 \\ (29)^2=(20)^2+(21)^2\end{aligned}\)
A continuación, cuadrar cada uno de los términos indicados en la ecuación.
\(\begin{aligned} (29)^2&=(20)^2+(21)^2 \\ (29\times 29)&=(20\times 20)+(21\times 21) \end{aligned}\)
A continuación, evalúe cada uno de los cuadrados y simplifique la ecuación.
\(\begin{aligned} (29\times 29)&=(20\times 20)+(21\times 21) \\ 841&=400+441 \\ 841&=841\end{aligned}\)
El cuadrado de la longitud de un lado del triángulo es igual a la suma de los cuadrados de las longitudes de los otros dos lados. El jardín es un triángulo rectángulo.
Brandon puede usar la cerca de su abuelo para su jardín de flores.
¿El conjunto de números (5, 8, 10) son los largos de los lados de un triángulo rectángulo?
Solución
Primero, determine los valores para cada lado del triángulo rectángulo. La longitud del lado más largo representará 'c', la hipotenusa. Las otras dos longitudes representarán las longitudes de las patas 'a' y 'b'.
\(\begin{aligned} a&=5 \\ b&=8 \\ c&=10 \end{aligned}\)
A continuación, sustituir los valores dados en el Teorema de Pitágoras.
\(\begin{aligned} c^2&=a^2+b^2 \\ (10)^2&=(5)^2+(8)^2 \end{aligned}\)
A continuación, cuadrar cada uno de los términos indicados en la ecuación.
\(\begin{aligned} (10)^2&=(5)^2+(8)^2 \\ (10\times 10)&=(5\times 5)+(8\times 8) \end{aligned}\)
A continuación, evalúe cada una de las casillas.
\(\begin{aligned} (10\times 10)&=(5\times 5)+(8\times 8) \\ 100&=25+64 \end{aligned}\)
Después, simplifique el lado derecho de la ecuación sumando los números.
\(\begin{aligned} 100&=25+64 \\ 100&\neq 89\end{aligned}\)
Ambos lados de la ecuación no son iguales. El cuadrado de la longitud de un lado del triángulo NO es igual a la suma de los cuadrados de las longitudes de los otros dos lados.
El conjunto de números (5, 8, 10) no son las longitudes de los lados de un triángulo rectángulo.
¿El siguiente triángulo (que puede o no ser dibujado a escala) es un triángulo rectángulo?
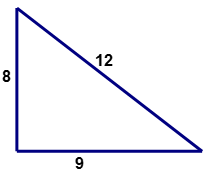
Solución
Primero, determinar los valores para (a, b, c) de un triángulo rectángulo. El lado más largo representará 'c' la hipotenusa.
\(\begin{aligned} a&=8 \\ b&=9 \\ c&=12 \end{aligned}\)
A continuación, sustituir los valores dados en el Teorema de Pitágoras.
\(\begin{aligned} c^2&=a^2+b^2 \\ (12)^2&=(8)^2+(9)^2 \end{aligned}\)
A continuación, cuadrar cada uno de los términos indicados en la ecuación.
\(\begin{aligned} (12)^2&=(8)^2+(9)^2 \\ (12\times 12)&=(8\times 8)+(9\times 9) \end{aligned}\)
A continuación, evalúe cada una de las casillas.
\(\begin{aligned} (12\times 12)&=(8\times 8)+(9\times 9) \\ 144&=64+81 \end{aligned}\)
Después, simplifique el lado derecho de la ecuación sumando los números.
\(\begin{aligned}144&=64+81 \\ 144 &\neq 145\end{aligned} \)
Ambos lados de la ecuación no son iguales. El cuadrado de la longitud de un lado del triángulo NO es igual a la suma de los cuadrados de las longitudes de los otros dos lados. El triángulo no es un triángulo rectángulo.
¿El siguiente triángulo (que puede o no ser dibujado a escala) es un triángulo rectángulo?
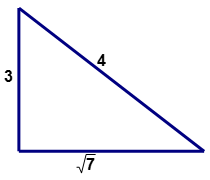
Solución
Primero, determinar los valores para (a, b, c) de un triángulo rectángulo. El lado más largo representará 'c' la hipotenusa.
\(\begin{aligned}\sqrt{7}&\approx 2.65\\ a&=3 \\ b&=\sqrt{7} \\ c&=4\end{aligned}\)
A continuación, sustituir los valores dados en el Teorema de Pitágoras.
\(\begin{aligned} c^2&=a^2+b^2 \\ (4)^2&=(3)^2+(\sqrt{7})^2 \end{aligned}\)
A continuación, cuadrar cada uno de los términos indicados en la ecuación.
\(\begin{aligned} (4)^2&=(3)^2+(\sqrt{7})^2 \\ (4\times 4)&=(3\times 3)+(\sqrt{7}\times \sqrt{7}) \end{aligned}\)
A continuación, evalúe cada una de las casillas.
\(\begin{aligned} (4\times 4)=(3\times 3)+(\sqrt{7}\times \sqrt{7}) \\ 16&=9+7\end{aligned}\)
Después, simplifique el lado derecho de la ecuación sumando los números.
\(\begin{aligned} 16&=9+7 \\ 16&=16 \end{aligned}\)
Ambos lados de la ecuación son iguales. El cuadrado de la longitud de un lado del triángulo es igual a la suma de los cuadrados de las longitudes de los otros dos lados. El triángulo es un triángulo rectángulo.
Revisar
Piensa en lo que has aprendido sobre el Teorema de Pitágoras y responde verdadero o falso para las siguientes preguntas.
1. El Teorema de Pitágoras trabajará para un triángulo agudo con todos los ángulos de 60°.
2. El Teorema de Pitágoras trabajará para un triángulo rectángulo.
3. El Teorema de Pitágoras sólo funcionará si el triángulo es un triángulo rectángulo.
4. Las patas de un triángulo rectángulo se consideran los dos lados más cortos del triángulo rectángulo.
5. La hipotenusa es el lado más largo de un triángulo rectángulo.
6. Lo contrario del Teorema de Pitágoras se utiliza para encontrar las medidas angulares de un triángulo obtuso.
7. Un triple pitagórico es cuando multiplicas todas las medidas de ángulo por tres.
8. Puedes usar el Teorema de Pitágoras para averiguar si las longitudes laterales de un triángulo lo convierten en un triángulo rectángulo o no.
Identificar si cada uno de los siguientes valores es o no un Triple Pitagórico. Escribe sí o no para tu respuesta.
9. (4, 5, 6)
10. (6, 8, 10)
11. (5, 6, 9)
12. (9, 12, 15)
13. (30, 40, 55)
14. (21, 28, 35)
15. (12, 16, 20).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.7.
Recursos
Recursos adicionales
Video: El teorema de Pitágoras y Lo Converso del Teorema de Pitágoras
Práctica: Conversación del Teorema de Pitágoras

