1.9:30-60-90 Triángulos Rectos
- Page ID
- 107679
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La hipotenusa equivale al doble de la pierna más pequeña, mientras que la pierna más grande\(sqrt{3}\) es por la menor.
Uno de los dos triángulos rectos especiales se llama triángulo 30-60-90, después de sus tres ángulos.
30-60-90 Teorema: Si un triángulo tiene medidas de ángulo\(30^{\circ}\),\(60^{\circ}\) y\(90^{\circ}\), entonces los lados están en la relación\(x: x\sqrt{3}:2x\).
La pierna más corta es siempre\(x\), la pierna más larga es siempre\(x\sqrt{3}\), y la hipotenusa es siempre\(2x\). Si alguna vez olvidas estos teoremas, aún puedes usar el Teorema de Pitágoras.
¿Y si te dieran un triángulo rectángulo 30-60-90 y la longitud de uno de sus lados? ¿Cómo podrías averiguar las longitudes de sus otros lados?
Encuentra el valor de\(x\) y\(y\).
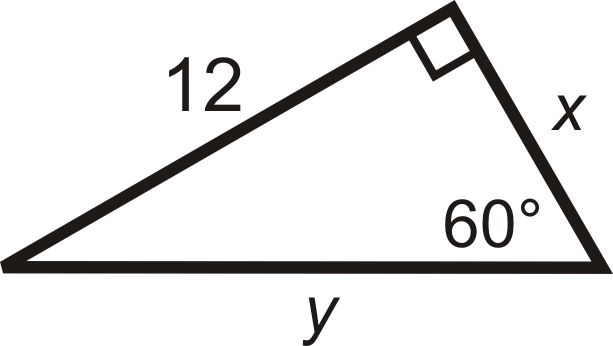
Solución
Se nos da la pierna más larga.
\(\begin{aligned} x\sqrt{3} &=12 \\ x&=12\sqrt{3}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}=12\dfrac{\sqrt{3}}{3}=4\sqrt{3} \\ \text{The hypotenuse is } y&=2(4\sqrt{3})=8\sqrt{3} \end{aligned}\)
Encuentra el valor de\(x\) y\(y\).
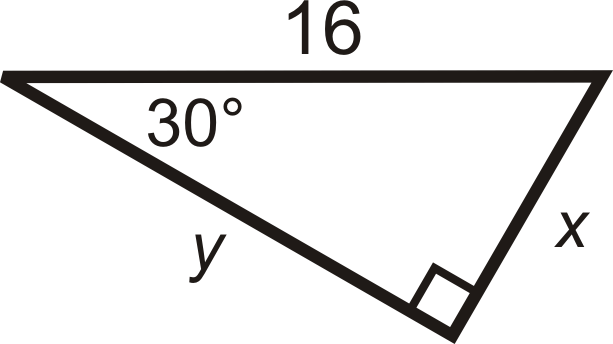
Solución
Se nos da la hipotenusa.
\(\begin{aligned} 2x&=16 \\ x&=8 \\ \text{The longer leg is } y&=8\cdot \sqrt{3}&=8\sqrt{3} \end{aligned} \)
Encuentra la longitud de los lados faltantes.
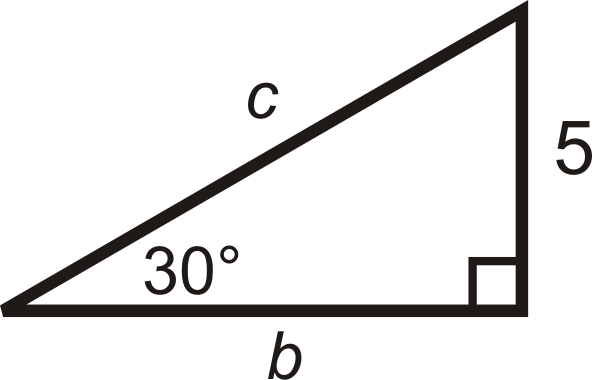
Solución
Se nos da la pierna más corta. Si\(x=5\), entonces la pierna más larga,\(b=5\sqrt{3}\), y la hipotenusa,\(c=2(5)=10\).
Encuentra la longitud de los lados faltantes.
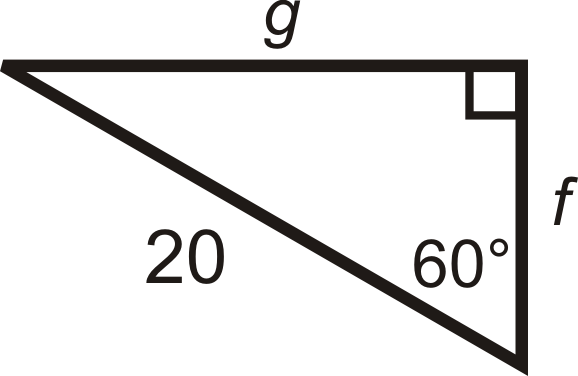
Solución
Se nos da la hipotenusa. \(2x=20\), entonces la pierna más corta,\(f=\dfrac{20}{2}=10\), y la pierna más larga,\(g=10\sqrt{3}\).
Un rectángulo tiene lados 4 y\(4\sqrt{3}\). ¿Cuál es la longitud de la diagonal?
Solución
Si no te dan una imagen, dibuja una.
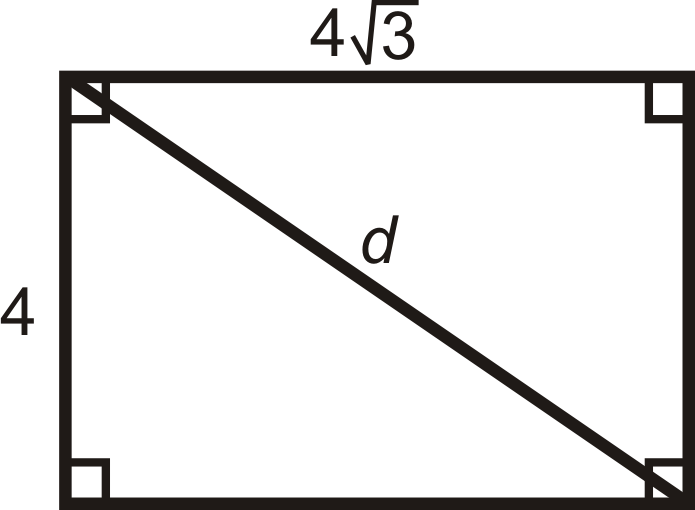
Las dos longitudes son\(x\),\(x\sqrt{3}\), entonces la diagonal sería\(2x\), o\(2(4)=8\).
Si no reconociste que este es un triángulo 30-60-90, también puedes usar el Teorema de Pitágoras.
\(\begin{aligned} 4^2+(4\sqrt{3})^2&=d^2 \\ 16+48&=d^2 \\ d=\sqrt{64}&=8 \end{aligned}\)
Revisar
- En un triángulo 30-60-90, si la pierna más corta es 5, entonces la pierna más larga es __________ y la hipotenusa es ___________.
- En un triángulo 30-60-90, si la pierna más corta es\(x\), entonces la pierna más larga es __________ y la hipotenusa es ___________.
- Un rectángulo tiene lados de longitud 6 y\(6\sqrt{3}\). ¿Cuál es la longitud de la diagonal?
- Dos lados (opuestos) de un rectángulo son 10 y la diagonal es 20. ¿Cuál es la longitud de los otros dos lados?
Para las preguntas 5-12, encuentra los largos de los lados faltantes. Simplifica todos los radicales.
-
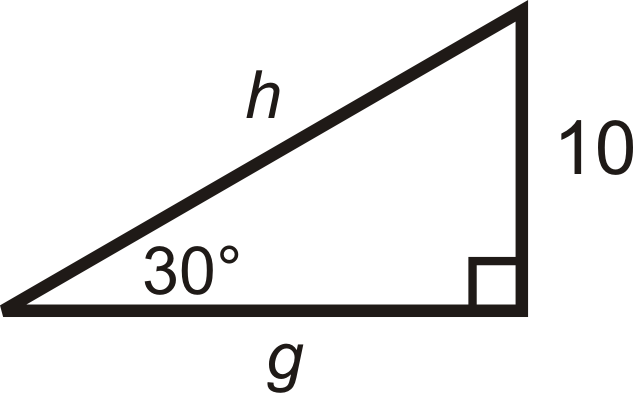
Figura\(\PageIndex{6}\) -
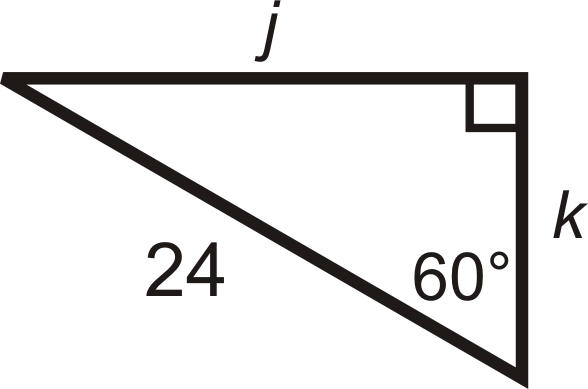
Figura\(\PageIndex{7}\) -
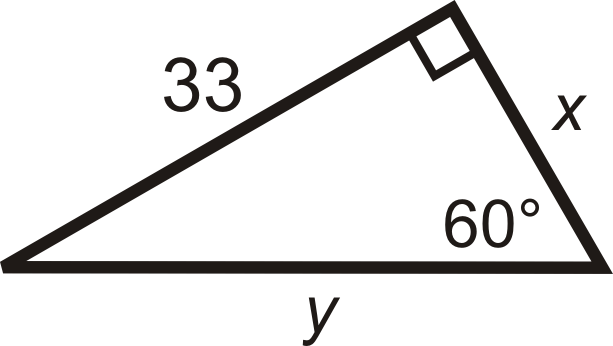
Figura\(\PageIndex{8}\) -
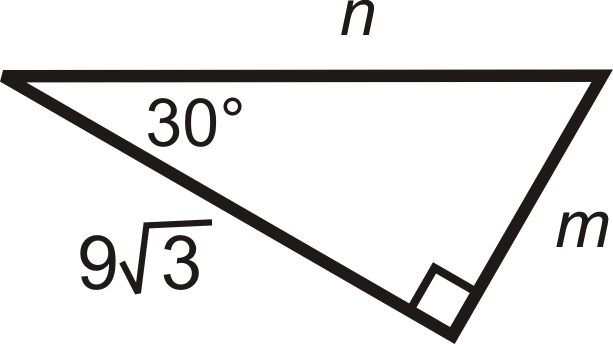
Figura\(\PageIndex{9}\) -
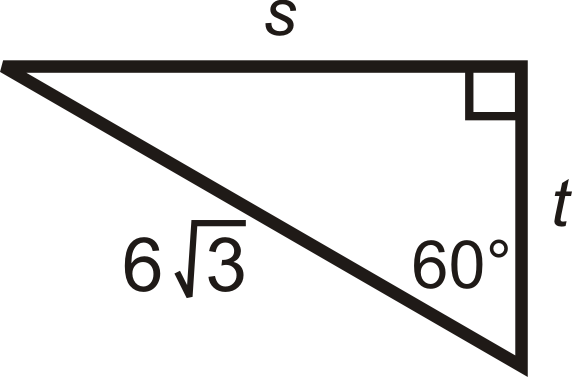
Figura\(\PageIndex{10}\) -
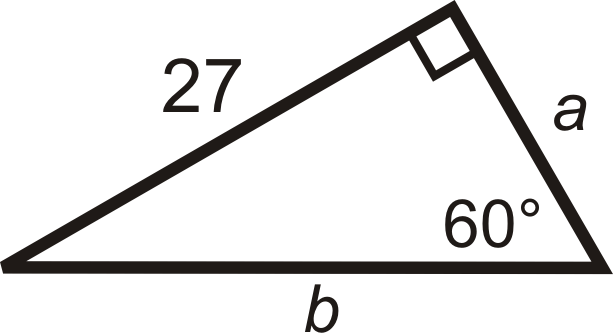
Figura\(\PageIndex{11}\) -
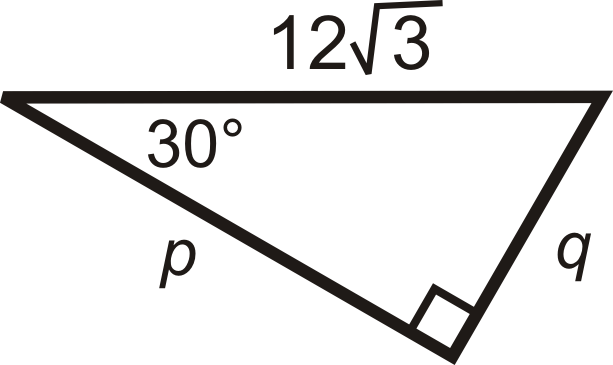
Figura\(\PageIndex{12}\) -
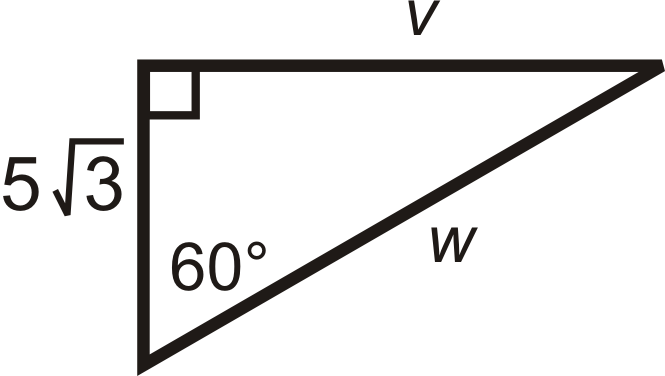
Figura\(\PageIndex{13}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.6.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Teorema 30-60-90 | Si un triángulo tiene medidas de ángulo de 30, 60 y 90 grados, entonces los lados están en la proporción\(x : x \sqrt{3} : 2x\) |
| Triángulo 30-60-90 | Un triángulo 30-60-90 es un triángulo rectángulo especial con ángulos de\(30^{\circ}\),\(60^{\circ}\), y\(90^{\circ}\). |
| Hipotenusa | La hipotenusa de un triángulo rectángulo es el lado más largo del triángulo rectángulo. Está frente al ángulo recto. |
| Piernas de un triángulo rectángulo | Las patas de un triángulo rectángulo son los dos lados más cortos del triángulo rectángulo. Las patas están adyacentes al ángulo recto. |
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
| Radical | El signo\(\sqrt{}\), o raíz cuadrada,. |
Recursos adicionales
Video: Resolviendo triángulos rectos especiales
Actividades: 30-60-90 Triángulos Rectos Preguntas de Discusión
Ayudas de estudio: Guía de estudio de triángulos rectos especiales
Práctica: Triángulos Rectos 30-60-90
Mundo real: Combatiendo la guerra contra las drogas usando geometría y triángulos especiales