2.2.5: Aplicaciones de las funciones trigonométricas inversas
- Page ID
- 107700
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Valores de ángulo en ejemplos del mundo real.
Estás trazando un viaje de senderismo a un nuevo lugar en el parque estatal cerca de tu casa. En tu mapa, sabes que se supone que debes ir en un curso que termina con que te hayas movido 2.5 millas al Este y 3 millas al Sur. Tu mapa, con los puntos de inicio y fin, se muestra aquí:
Ahora necesitas calcular el ángulo que necesitas para caminar con respecto al este debido. ¿Puedes encontrar una manera de calcular este ángulo usando funciones trigonométricas inversas?
Aplicación de funciones trigonométricas inversas
Los siguientes problemas son problemas del mundo real que se pueden resolver usando las funciones trigonométricas. En la vida cotidiana, la medición indirecta se utiliza para obtener respuestas a problemas que son imposibles de resolver utilizando herramientas de medición. No obstante, las matemáticas acudirán al rescate en forma de trigonometría para calcular estas mediciones desconocidas.
En un día frío de invierno el sol corre a través de la ventana de tu salón y provoca un ambiente cálido y calentito. Esto se debe al ángulo de inclinación del sol que afecta directamente el calentamiento y la refrigeración de los edificios. El mediodía es cuando el sol está a su altura máxima en el cielo y en este momento, el ángulo es mayor en el verano que en el invierno. Debido a esto, los edificios se construyen de tal manera que el voladizo del techo puede actuar como un toldo para dar sombra a las ventanas para que se enfríen en el verano y, sin embargo, permitir que los rayos del sol proporcionen calor en el invierno. Además de la construcción del edificio, el ángulo de inclinación del sol varía según la latitud de la ubicación del edificio.
Si se conoce la latitud de la ubicación, entonces se puede utilizar la siguiente fórmula para calcular el ángulo de inclinación del sol en cualquier fecha dada del año:
\(\text{Angle of sun}=90^{\circ}−\text{latitude}+−23.5^{\circ}\cdot \cos\left[(N+10)\dfrac{360}{365}\right]\)donde\(N\) representa el número del día del año que corresponde a la fecha del año. Nota: Esta fórmula es precisa para\(\pm \dfrac{1^{\circ}}{2}\)
Determinar la medición del ángulo de inclinación del sol para un edificio ubicado a una latitud de\(42^{\circ}\),\(10^{th}, the \(69^{th}\) día de marzo del año.
\ (\ begin {array} {l}
\ text {Ángulo del sol} =90^ {\ circ} -42^ {\ circ} +-23.5^ {\ circ}\ cdot\ cos\ izquierda [(69+10)\ dfrac {360} {365}\ derecha]\
\ text {Ángulo del sol} =48^ {\ circ} +-23.5^ {\ circ} +-23.5^ {\ c} (0.2093)
\\\ text {Ángulo de sol} =48^ {\ circ} -4.92^ {\ circ}\\
\ text {Ángulo de}\ nombreoperador {sol} =43.08^ {\ circ}
\ end {array}\)
Determinar la medición del ángulo de inclinación del sol para un edificio ubicado a una latitud de\(20^{\circ}\), septiembre\(21^{st}\).
\ (\ begin {array} {l}
\ text {Ángulo del sol} =90^ {\ circ} -20^ {\ circ} +-23.5^ {\ circ}\ cdot\ cos\ izquierda [(264+10)\ dfrac {360} {365}\ derecha]\\ text {Ángulo del sol} =70^ {
\ circ} +-23.5^ {\ circ} +-23.5^ {\ c} (0.0043)\
\\ text {Ángulo del sol} =70.10^ {\ circ}
\ end {array}\)
Uso de funciones trigonométricas inversas
1. Una torre, de 28.4 pies de altura, debe asegurarse con un cable de sujeción anclado a 5 pies de la base de la torre. ¿Qué ángulo hará el cable de sujeción con el suelo?
Dibuja un cuadro.
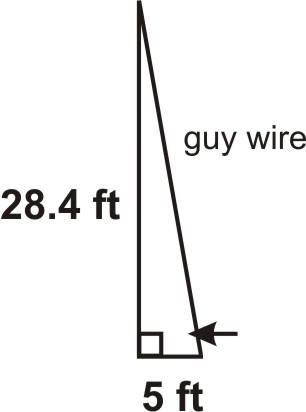
\ (\ begin {alineado}
\ tan\ theta &=\ dfrac {o p p} {a d j}\\
\ tan\ theta &=\ dfrac {28.4} {5}\\
\ tan\ theta &=5.68\
\\ tan ^ {-1} (\ tan\ theta) &=\ tan ^ {-1} (5.68)\
\\ theta &=02^ {\ circ}
\ final {alineado}\)
El siguiente problema que involucra funciones y sus inversos se resolverá utilizando la propiedad\(f(f^{−1}(x))=f^{−1}(f(x))\). Además, también se utilizará la tecnología para completar la solución.
2. En la sala principal de la arena local, hay varias pantallas de visualización que están disponibles para ver para que no te pierdas ninguna de las acciones en el hielo. La parte inferior de una pantalla está a 3 pies por encima del nivel de los ojos y la pantalla en sí tiene 7 pies de altura. El ángulo de visión (inclinación) se forma mirando tanto la parte inferior como la parte superior de la pantalla.
Haga un boceto de una imagen para representar este problema.
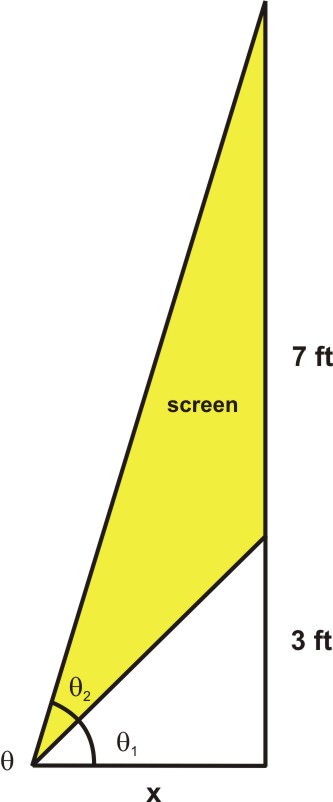
Calcula la medida del ángulo de visión que resulta de mirar la parte inferior y luego la parte superior de la pantalla. ¿A qué distancia de la pantalla se produce el valor máximo para el ángulo de visión?
\ (\ begin {alineado}
\ theta_ {2} &=\ tan\ theta-\ tan\ theta_ {1}\\
\ tan\ theta &=\ dfrac {10} {x}\ texto {y}\ tan\ theta_ {1} =\ dfrac {3} {x}\
\ theta_ {2} &=\ tan ^ {-1}\ izquierda (\ dfrac {10} {x}\ derecha) -\ tan ^ {-1}\ izquierda (\ dfrac {3} {x}\ derecha)
\ end {alineado}\)
Para determinar estos valores, utilice una calculadora gráfica y la función de rastreo para determinar cuándo ocurre el máximo real.
De la gráfica, se puede ver que el máximo ocurre cuando\(x\approx 5.59\text{ ft}\). y\(\theta\approx 32.57^{\circ}\).
Antes, se le pidió que calculara el ángulo que necesita para caminar con respecto al este debido.
Solución
Se puede configurar un triángulo que coincida con la situación física de este problema. Así es como debería verse:
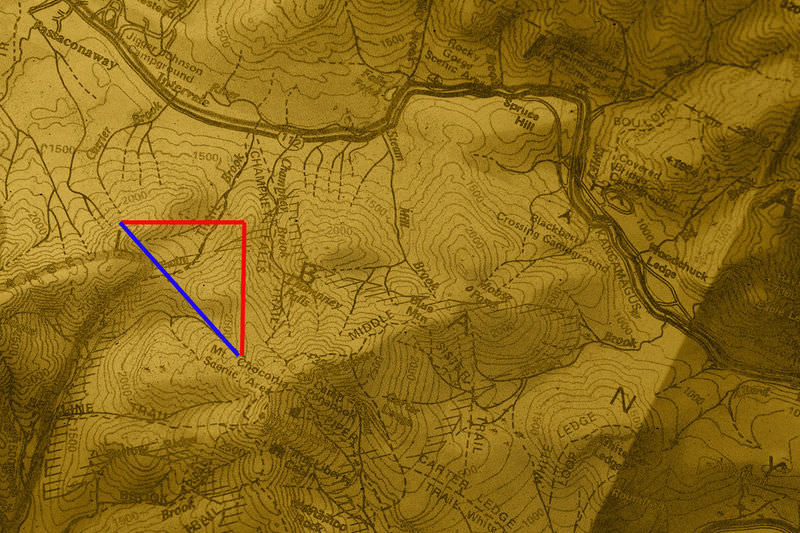
Usando la función tangente, puede resolver el ángulo que necesita encontrar:
\(\begin{aligned} \theta&= \tan^{−1}\left(\dfrac{3}{−2.5}\right) \\ \theta&=−50.19 \end{aligned}\)
La intensidad de cierto tipo de luz polarizada viene dada por la ecuación\(I=I_0 \sin 2\theta \cos 2\theta\).
Resolver para\(\theta\).
Solución
\ (\ begin {alineado}
I &=I_ {0}\ sin 2\ theta\ cos 2\ theta\
\ dfrac {I} {I_ {0}} &=\ dfrac {I_ {0}} {I_ {0}}\ sin 2\ theta\ cos 2\ theta\
\ dfrac {I} {I_ {0}} &= sin 2\ theta\ cos 2\ theta\
\ dfrac {2 I} {I_ {0}} &=2\ sin 2\ theta\ cos 2\ theta\\
\ dfrac {2 I} {I_ {0}} &=\ sin 4\ theta\\
\ sin ^ {-1}\ dfrac {2 I} {I_ {0}} &=4\ theta\
\ dfrac {1} {4}\ sin ^ {-1}\ dfrac {2 I} {I_ {0}} &=\ theta
\ end {alineado}\)
El siguiente diagrama representa los extremos de un canal de agua. Los extremos son en realidad trapezoides isósceles, y la longitud del canal desde extremo a extremo es de diez pies. Determinar el volumen máximo del canal y el valor de\(\theta\) que maximiza ese volumen.
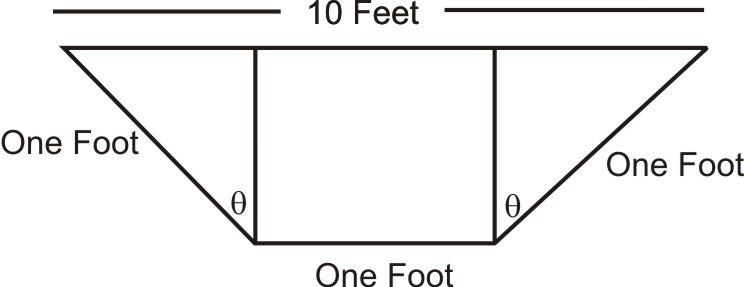
Solución
El volumen es de 10 pies por el área del extremo. El extremo consta de dos triángulos rectos congruentes y un rectángulo. El área de cada triángulo rectángulo es\(\dfrac{1}{2}(\sin \theta)(\cos \theta)\) y la del rectángulo es\((1)(\cos \theta)\). Esto significa que el volumen puede ser determinado por la función\(V(\theta)=10(\cos \theta+ \sin \theta \cos\theta)\), y esta función se puede graficar de la siguiente manera para encontrar el volumen máximo y el ángulo\(\theta\) donde ocurre.
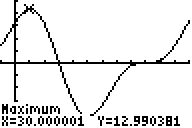
Por lo tanto, el volumen máximo es de aproximadamente 13 pies cúbicos y ocurre cuando\(\theta\) se trata de\(30^{\circ}\).
Un barco está atracado al final de un muelle de 10 pies. El barco sale del muelle y deja caer el ancla a 230 pies de distancia a 3 pies directamente de la costa (que es perpendicular al muelle). ¿Cuál fue el rumbo de la embarcación desde una línea trazada desde el final del muelle hasta el pie del muelle?
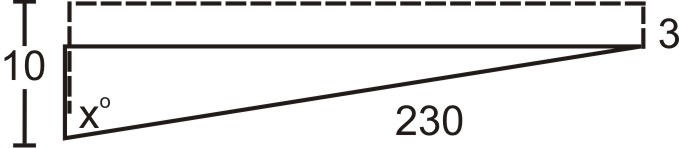
Solución
\(\begin{aligned} \cos x &=\dfrac{7}{230}\rightarrow x=\cos^{−1} \dfrac{7}{230}\\ x&= 88.26^{\circ} \end{aligned}\)
Revisar
- La distancia de un barco a un faro es de 100 pies y el faro mide 120 pies de altura. Cuál es el ángulo de depresión desde lo alto del Faro hasta el barco.
- Estás parado a 100 pies de un arco que mide 68 pies de altura. ¿En qué ángulo hay que mirar hacia arriba para ver la parte superior del arco? Supongamos que mide 5 pies de altura.
- El ángulo de elevación de la parte superior de una iglesia a un punto a 100 pies de distancia de la base es\(60^{\circ}\). Encuentra la altura de la iglesia.
Estás de pie mirando un cuadro grande en la pared. El fondo de la pintura está a 1 pie por encima del nivel de tus ojos. El cuadro mide 10 pies de altura. Supongamos que estás parado a\(x\) pies de la pintura y ese ángulo\ theta está formado por las líneas de visión hacia el fondo y hacia la parte superior de la pintura.
- Dibuja un cuadro para representar esta situación.
- Resolver para\(\theta\) en términos de\(x\).
- Si estás parado a 10 pies de la pintura, ¿qué es\ theta?
- Si\(\theta=30^{\circ}\), ¿a qué distancia estás parado de la pared (al pie más cercano)?
Estás viendo un globo aerostático que estaba a 300 pies de ti cuando empezó a elevarse del suelo. Supongamos que la altura del globo\(\theta\) es\(x\) y es el ángulo de elevación desde el suelo donde se encuentra de pie hasta el globo.
- Resolver para\(x\) en términos de\(\theta\).
- Resolver para\(\theta\) en términos de\(x\).
- ¿Cuál es el ángulo de elevación cuando el globo aerostático se encuentra a 500 pies sobre el suelo?
- ¿Qué tan alto sobre el suelo está el globo cuando el ángulo de elevación es 80^ {\ circ}?
Recordemos que si se conoce la latitud de la ubicación, entonces se puede utilizar la siguiente fórmula para calcular el ángulo de inclinación del sol en cualquier fecha dada del año:
\(\text{Angle of sun}=90^{\circ}−\text{latitude}+−23.5^{\circ} \cdot cos[(N+10)\dfrac{360}{365}]\)donde\(N\) representa el número del día del año que corresponde a la fecha del año.
- Determinar la medición del ángulo de inclinación del sol para un edificio ubicado a una latitud de\(30^{\circ}\), abril\(12^{th}\), el\(102^{th}\) día del año.
- Determinar la medición del ángulo de inclinación del sol para un edificio ubicado a una latitud de\(50^{\circ}\)\(14^{th}\), agosto,\(226^{th}\) día del año.
- Una torre, de 50 pies de altura, está asegurada con un cable de sujeción anclado a 8 pies de la base de la torre. ¿Qué ángulo hará el cable de sujeción con el suelo?
- Un asta de bandera de 30 pies de altura proyecta una sombra de 12 pies. ¿Cuál es el ángulo que el sol golpea el asta de la bandera?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.10.
vocabulario
| Término | Definición |
|---|---|
| función trigonométrica inversa | Una función trigonométrica inversa es una función que invierte una función trigonométrica, dejando como resultado el argumento de la función trigonométrica original. |
Recursos adicionales
Video: Problemas verbales de altura y distancia Aplicación de la trigonometría
Práctica: Aplicaciones de funciones trigonométricas inversas