2.2.4: Resolver triángulos rectos

Usando las funciones trigonométricas inversas para resolver la falta de información sobre los triángulos rectos.

Ratios trigonométricos inversos

En matemáticas, la palabra inversa significa “deshacer”. Por ejemplo, la suma y la resta son inversas entre sí porque una deshace a la otra. Cuando utilizamos las relaciones trigonométricas inversas, podemos encontrar medidas de ángulo agudo siempre y cuando se nos den dos lados.

Figura\(\PageIndex{1}\)

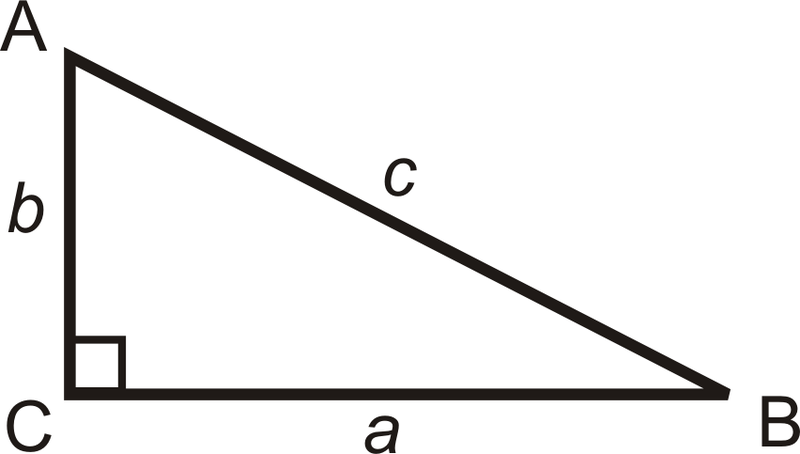
Tangente inversa: Etiquetado\(\tan ^{-1}\), el “-1” significa inverso.

\(\tan ^{-1} \left(\dfrac{b}{a}\right)=m\angle B\)y\(\tan ^{-1} \left(\dfrac{a}{b}\right)=m\angle A.\)

Seno Inversa: Etiquetado\(\sin ^{-1}\).

\(\sin ^{-1} \left(\dfrac{b}{c}\right)=m\angle B\)y\(\sin ^{-1} \left(\dfrac{a}{c}\right)=m\angle A.\)

Coseno inverso: Etiquetado\(\cos ^{-1}\).

\(\cos ^{-1} \left(\dfrac{a}{c}\right)=m\angle B\)y\(\cos ^{-1} \left(\dfrac{b}{c}\right)=m\angle A.\)

En la mayoría de los problemas, para encontrar la medida de los ángulos necesitarás usar tu calculadora. En la mayoría de las calculadoras científicas y gráficas, los botones se ven como\([\sin ^{-1}]\),\([\cos ^{-1}]\), y\([\(\tan ^{-1}]\). También es posible que tengas que presionar un botón de turno o segundo para acceder a estas funciones.

Ahora que conoces tanto las relaciones trigonométricas como las relaciones trigonométricas inversas puedes resolver un triángulo rectángulo. Para resolver un triángulo rectángulo, necesitas encontrar todos los lados y ángulos en él. Usualmente usarás seno, coseno o tangente; seno inverso, coseno inverso o tangente inversa; o el teorema de Pitágoras.

¿Y si te dijeran que la tangente de\(\angle Z\) es 0.6494? ¿Cómo podrías encontrar la medida de\(\angle Z\)?

Ejemplo\(\PageIndex{1}\)

Resuelve el triángulo rectángulo.

Figura\(\PageIndex{2}\)

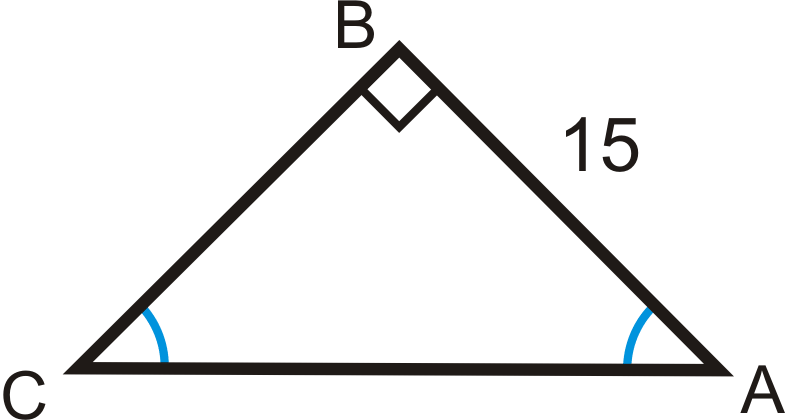
Solución

Los dos ángulos agudos son congruentes, haciéndolos ambos\(45^{\circ}\). Se trata de un triángulo 45-45-90. Se pueden utilizar las relaciones trigonométricas o las relaciones especiales de triángulo rectángulo.

Relaciones trigonométricas

\ (\ begin {array} {rlrl}
\ tan 45^ {\ circ} & =\ dfrac {15} {B C} &\ sin 45^ {\ circ} & =\ dfrac {15} {A C}\\
B C & =\ dfrac {15} {\ tan 45^ {\ circ}} =15 & A C & =\ dfrac {15} {\ sin 45^ {\ circ}}\ aprox 21.21
\ fin {array}\)

Relaciones de triángulo 45-45-90

\(BC=AB=15 \text{, } AC=15\sqrt{2} \approx 21.21\)

Ejemplo\(\PageIndex{2}\)

Usa los lados del triángulo y tu calculadora para encontrar el valor de\(\angle A\). Redondee su respuesta al décimo de grado más cercano.

Figura\(\PageIndex{3}\)

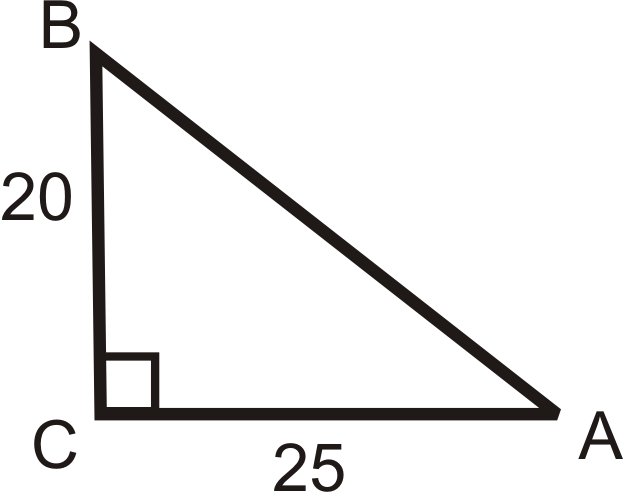
Solución

En referencia a\(\angle A\), se nos da la pierna opuesta y la pierna adyacente. Esto significa que debemos usar la relación tangente.

\(\tan A=\dfrac{20}{25}=\dfrac{4}{5}\). Entonces,\(\tan ^{-1} \dfrac{4}{5}=m\angle A\). Ahora, usa tu calculadora.

Si estás usando un TI-83 o 84, las pulsaciones de teclas serían: [2nd] [TAN] (\(\dfrac{4}{5}\)) [ENTER] y la pantalla se ve así:

Figura\(\PageIndex{4}\)

\(m\angle A \approx 38.7^{\circ}\)

Ejemplo\(\PageIndex{3}\)

\(\angle A\)es un ángulo agudo en un triángulo rectángulo. Encontrar\(m\angle A\) al décimo de grado más cercano para\(\sin A=0.68\),\(\cos A=0.85\), y\(\tan A=0.34\).

Solución

\(\begin{aligned} m\angle A&=\sin ^{-1} 0.68\approx 42.8^{\circ} \\ m\angle A&=\cos ^{-1} 0.85\approx 31.8^{\circ} \\ m\angle A&=\tan ^{-1} 0.34\approx 18.8^{\circ} \end{aligned}\)

Ejemplo\(\PageIndex{4}\)

Resuelve el triángulo rectángulo.

Figura\(\PageIndex{5}\)

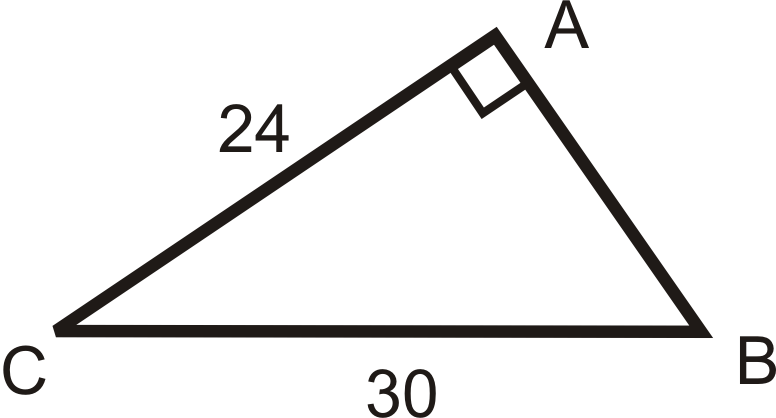
Solución

Para resolver este triángulo rectángulo, necesitamos encontrar\(AB\),\(m\angle C\) y\(m\angle B\). Usa solo los valores que te den.

\(\underline{AB}: \text{ Use the Pythagorean Theorem.}\)

\(\begin{aligned} 24^2+AB^2&=30^2 \\ 576+AB^2&=900 \\ AB^2&=324 \\ AB&=\sqrt{324}=18 \end{aligned}\)

\(\underline{m\angle B} : \text{ Use the inverse sine ratio.}\)

\(\begin{aligned} \sin B &=\dfrac{24}{30}=\dfrac{4}{5} \\ \sin ^{-1} (45) &\approx 53.1^{\circ} =m\angle B\end{aligned}\)

\(\underline{m\angle C} : \text{ Use the inverse cosine ratio.}\)

\(\cos C=\dfrac{24}{30}=\dfrac{4}{5} \rightarrow \cos ^{-1} (\dfrac{4}{5})\approx 36.9^{\circ} =m\angle C\)

Ejemplo\(\PageIndex{5}\)

¿Cuándo usarías el pecado y cuándo usarías\(\sin ^{-1}\)?

Solución

Usarías pecado cuando te dan un ángulo y estás resolviendo por un lado faltante. Lo usarías\(\sin ^{-1} \) cuando te dan lados y estás resolviendo un ángulo faltante.

Revisar

Usa tu calculadora para encontrar\(m\angle A\) al décimo de grado más cercano.

1. 
   

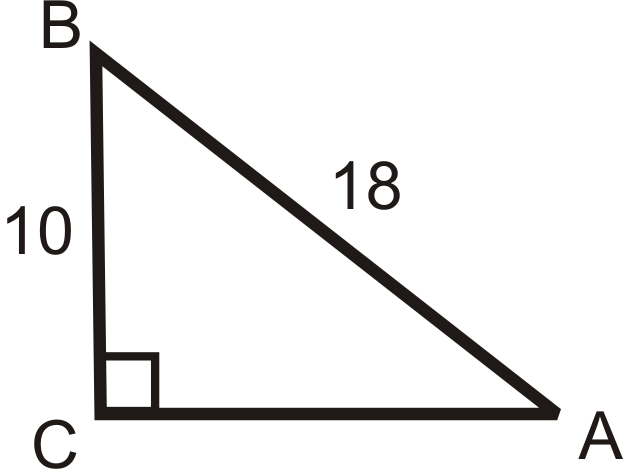
   Figura\(\PageIndex{6}\)

2. 

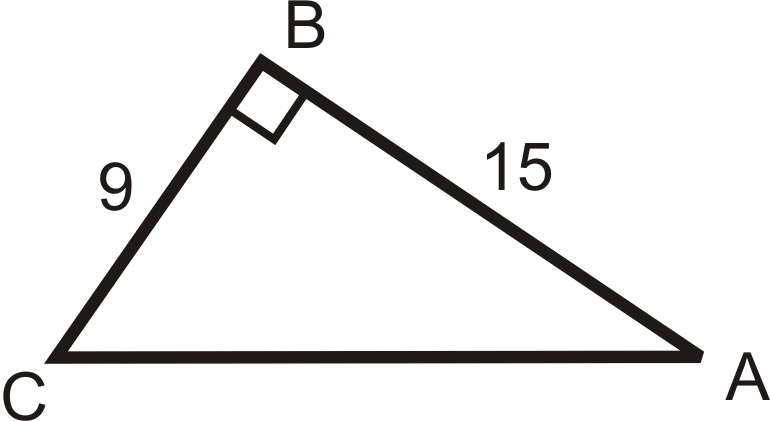
   Figura\(\PageIndex{7}\)

3. 

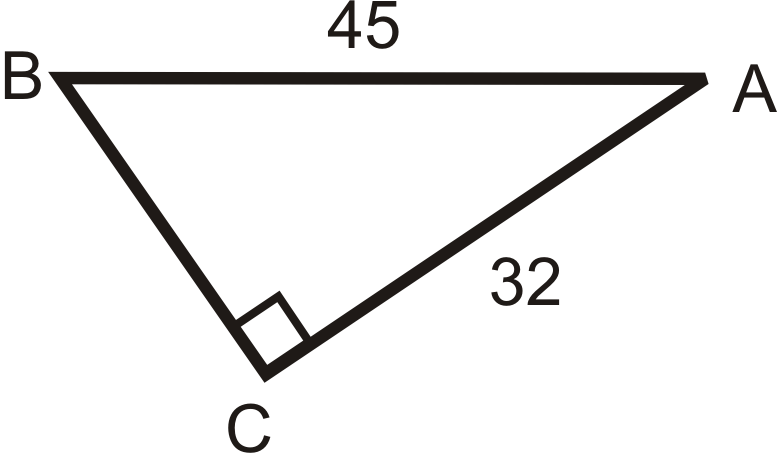
   Figura\(\PageIndex{8}\)

4. 

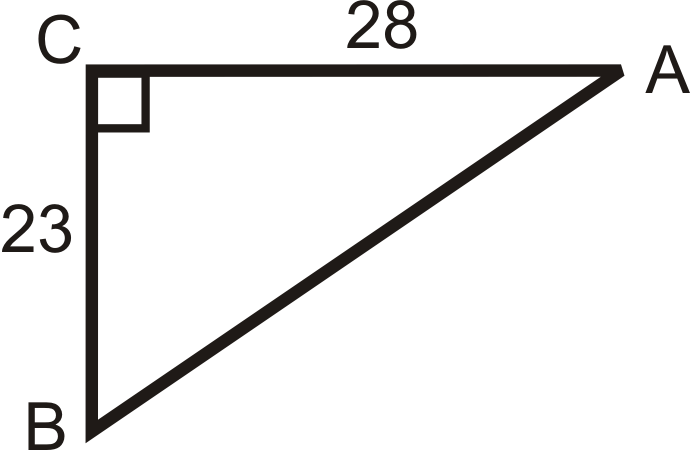
   Figura\(\PageIndex{9}\)

5. 

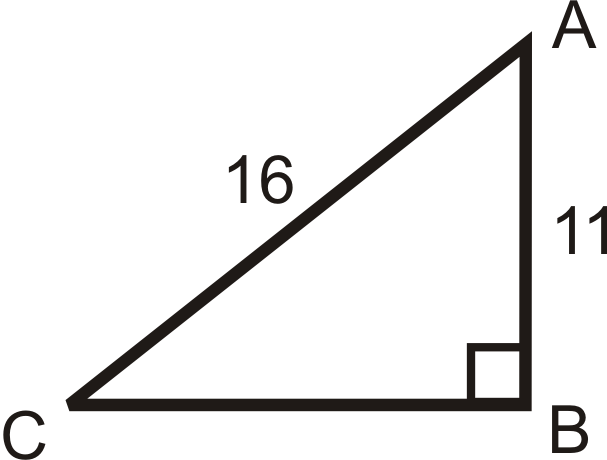
   Figura\(\PageIndex{10}\)

6. 

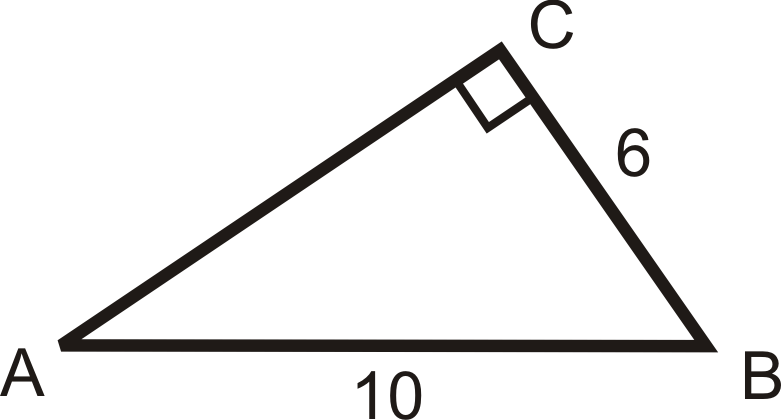
   Figura\(\PageIndex{11}\)

Dejar\(\angle A\) ser un ángulo agudo en un triángulo rectángulo. Encuentra\(m\angle A\) al décimo de grado más cercano.

7. \(\sin A=0.5684\)
8. \(\cos A=0.1234\)
9. \(\tan A=2.78\)
10. \(\cos ^{-1} 0.9845\)
11. \(\tan ^{-1} 15.93\)
12. \(\sin ^{-1} 0.7851\)

Resolviendo los siguientes triángulos rectos. Encuentra todos los lados y ángulos faltantes. Redondear cualquier respuesta decimal a la décima más cercana.

13. 
    

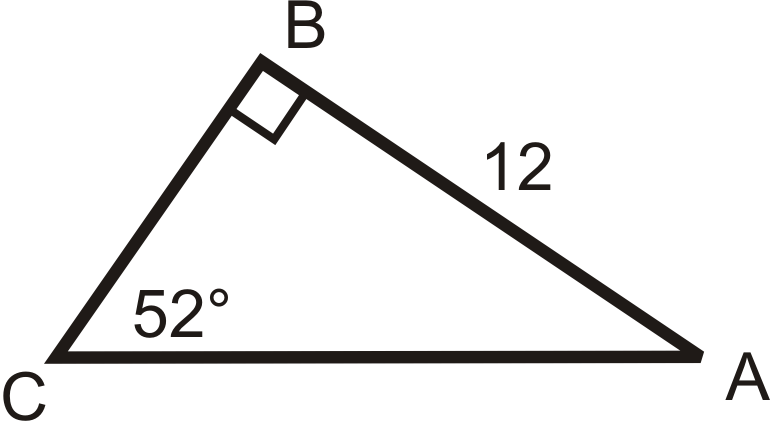
    Figura\(\PageIndex{12}\)

14. 

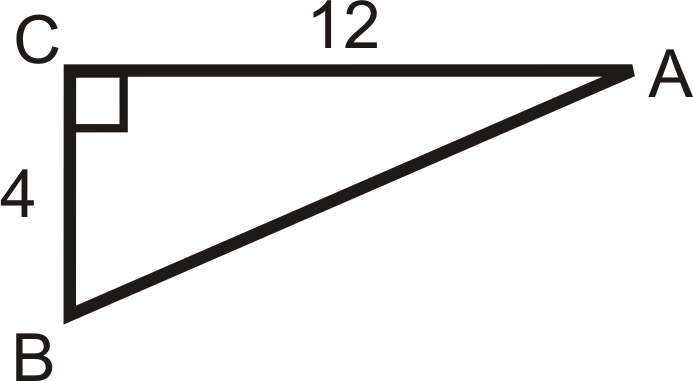
    Figura\(\PageIndex{13}\)

15. 

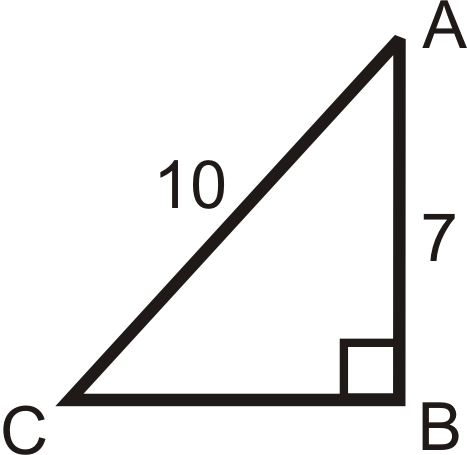
    Figura\(\PageIndex{14}\)

16. 

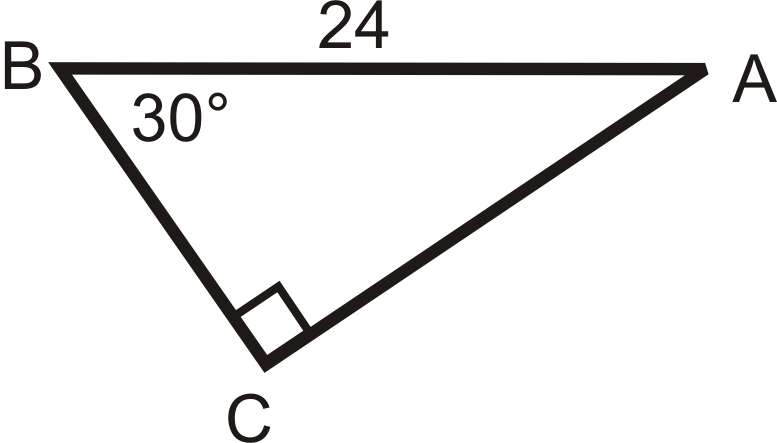
    Figura\(\PageIndex{15}\)

17. 

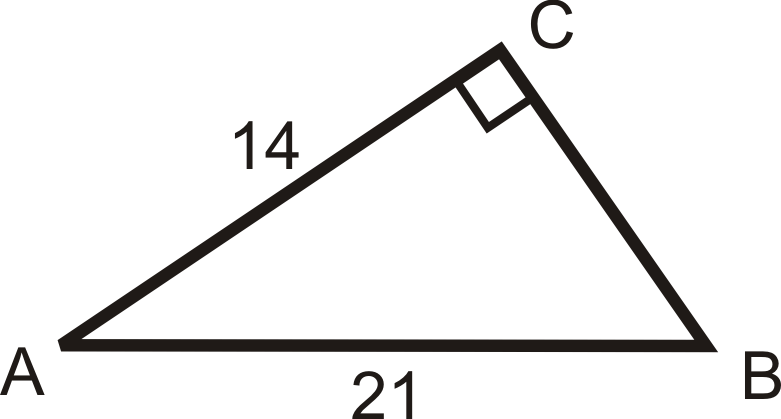
    Figura\(\PageIndex{16}\)

18. 

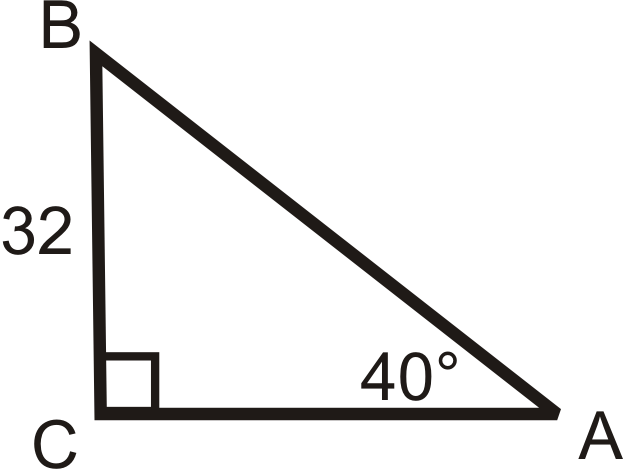
    Figura\(\PageIndex{17}\)

19. 

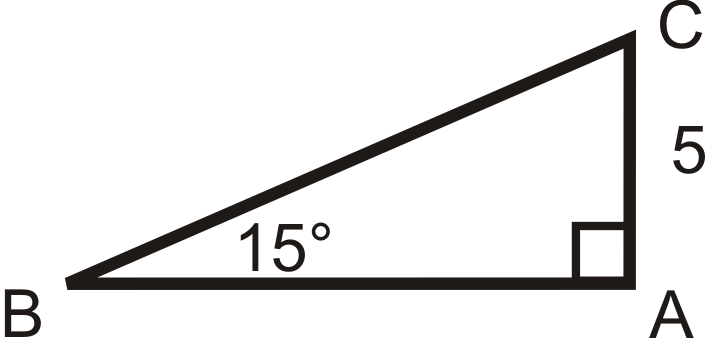
    Figura\(\PageIndex{18}\)

20. 

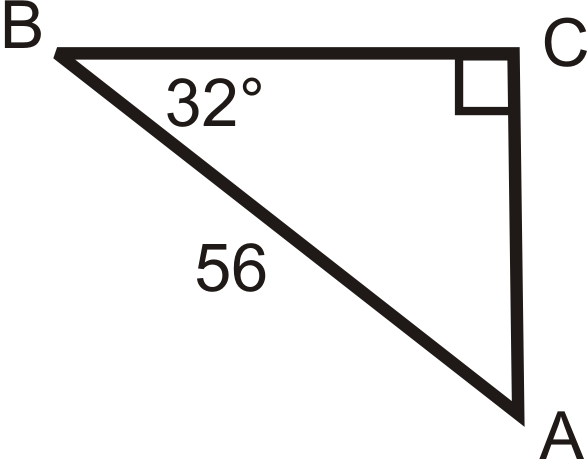
    Figura\(\PageIndex{19}\)

21. 

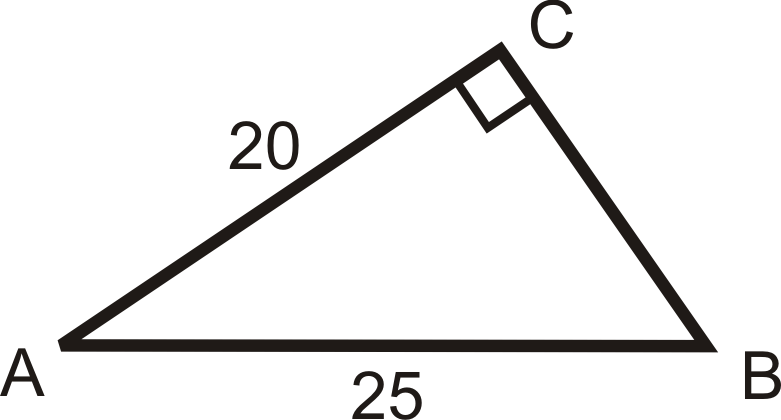
    Figura\(\PageIndex{20}\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.10.

Recursos adicionales

Elemento Interactivo

Video: Introducción a las funciones trigonométricas inversas

Actividades: Ratios trigonométricos inversos Preguntas de discusión

Ayudas de estudio: Guía de estudio de relaciones trigonométricas

Práctica: Resolver triángulos rectos