2.3.2: Medición de la rotación
- Page ID
- 107657
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Explore las relaciones triangulares de ángulos mayores a 90 grados
Introducción a los ángulos de rotación, ángulos coterminales y ángulos de referencia
¿En qué cuadrante se encuentra el lado terminal del ángulo\(−500^{\circ}\) y cuál es el ángulo de referencia para este ángulo?
Ángulos de rotación
Los ángulos de rotación se forman en el plano de coordenadas entre el\(x\) eje positivo (lado inicial) y un rayo (lado terminal). Las medidas de ángulo positivo representan una rotación en sentido antihorario mientras que los ángulos negativos indican una rotación en sentido horario
Dado que los\(y\) ejes\(x\) y son perpendiculares, cada eje representa entonces un incremento de noventa grados de rotación. Los diagramas a continuación muestran una variedad de ángulos formados por la rotación de un rayo a través de los cuadrantes del plano de coordenadas.
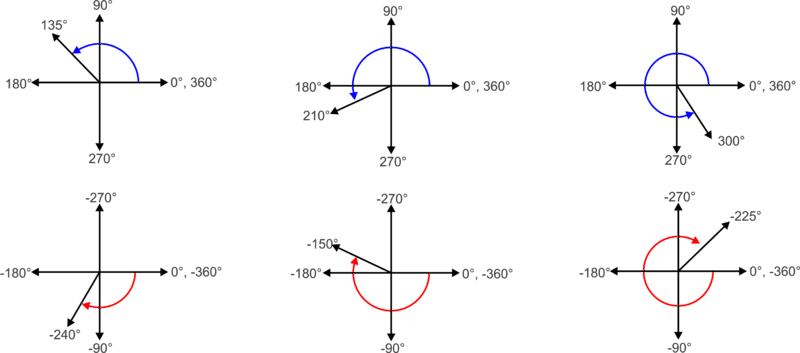
Un ángulo de rotación se puede describir infinitamente de muchas maneras. Se puede describir por un ángulo de rotación positivo o negativo o haciendo múltiples rotaciones de círculo completo a través de\(360^{\circ}\). El siguiente ejemplo ilustra este concepto.
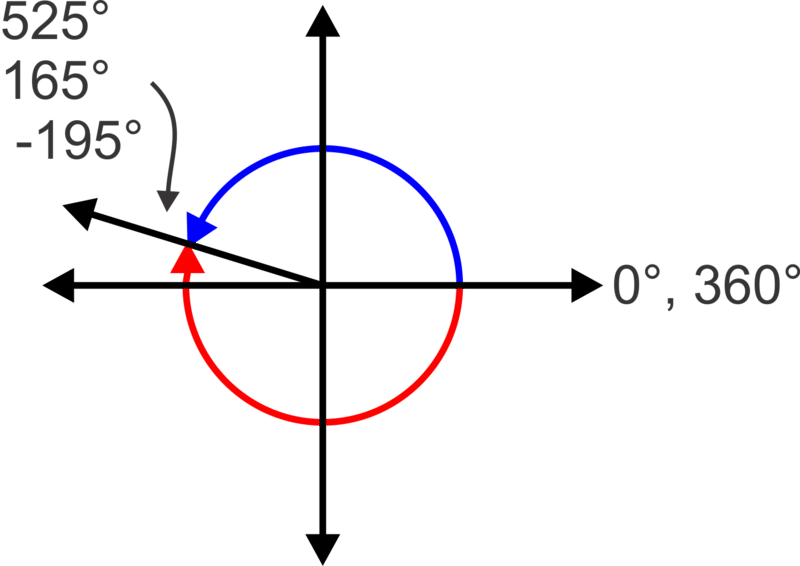
Para el ángulo\(525^{\circ}\), se realiza una\(360^{\circ}\) rotación completa y luego seguimos yendo otra\(165^{\circ}\) a\(525^{\circ}\). Por lo tanto, el ángulo resultante es equivalente a\(525^{\circ}−360^{\circ}\), o\(165^{\circ}\). En otras palabras, el lado terminal está en la misma ubicación que el lado terminal para un\(165^{\circ}\) ángulo. Si restamos de\(360^{\circ}\) nuevo, obtenemos un ángulo negativo,\(−195^{\circ}\). Como todos comparten el mismo lado terminal, se les llama ángulos coterminales.
Determinemos dos ángulos coterminales a\(837^{\circ}\), uno positivo y otro negativo.
Para encontrar ángulos coterminales simplemente sumamos o restamos\(360^{\circ}\) varias veces para obtener los ángulos que deseamos. \(837^{\circ}−360^{\circ}=477^{\circ}\), por lo que tenemos un ángulo coterminal positivo. Ahora podemos restar de\(360^{\circ}\) nuevo para conseguir\(477^{\circ}−360^{\circ}=117^{\circ}\).
Ángulo de referencia
Un ángulo de referencia es el ángulo agudo entre el lado terminal de un ángulo y el eje\(x \) —. El siguiente diagrama muestra los ángulos de referencia para los lados terminales de los ángulos en cada uno de los cuatro cuadrantes.
Nota: Un ángulo de referencia nunca está determinado por el ángulo entre el lado del terminal y el eje\(y\) —. Este es un error común para los estudiantes, especialmente cuando el lado terminal parece estar más cerca del eje\(y\) — que del\(x\) — eje.
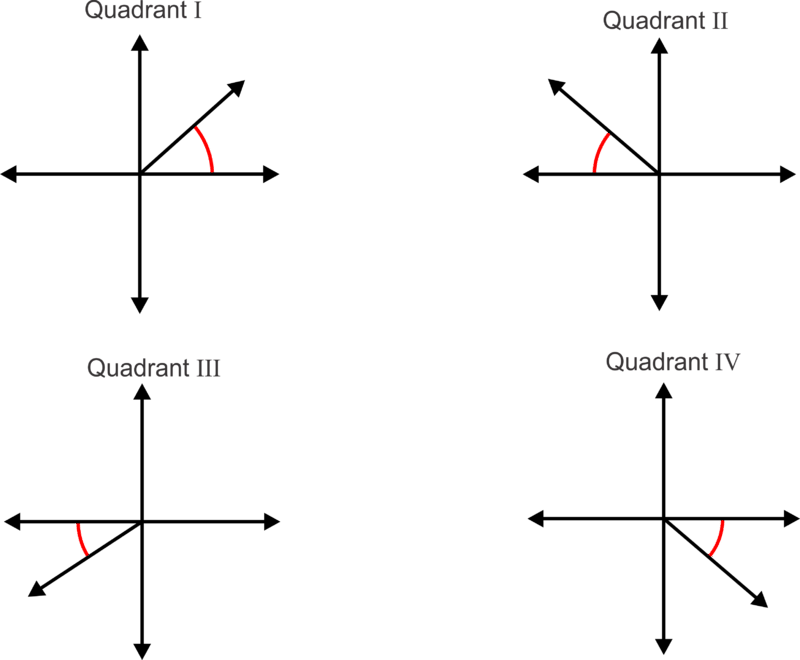
Ahora, determinemos el cuadrante en el que\(−745^{\circ}\) yace y de ahí determinemos el ángulo de referencia.
Dado que nuestro ángulo es de más de una rotación, necesitamos sumar\(360^{\circ}\) hasta que obtengamos un ángulo cuyo valor absoluto sea menor que\)\(360^{\circ}\):\(−745^{\circ}+360^{\circ}=−385^{\circ}\), de nuevo\(−385^{\circ}+360^{\circ}=−25^{\circ}\).
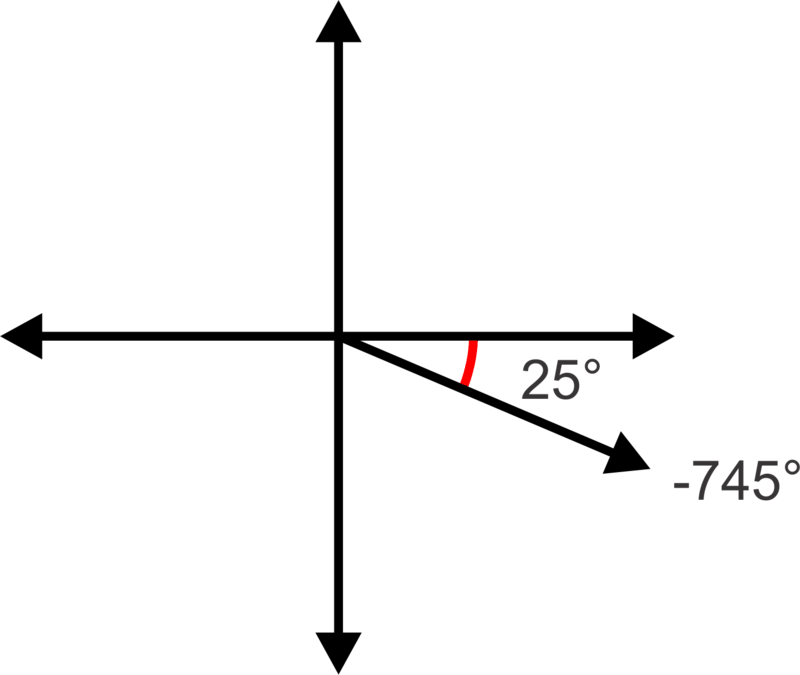
Ahora podemos trazar el ángulo y determinar el ángulo de referencia:
Tenga en cuenta que el ángulo de referencia es positivo\(25^{\circ}\). Todos los ángulos de referencia serán positivos ya que son ángulos agudos (entre\(0^{\circ}\) y\(90^{\circ}\)).
Finalmente, vamos a dar dos ángulos coterminales a\(595^{\circ}\), uno positivo y otro negativo, y encontrar el ángulo de referencia.
Para encontrar los ángulos coterminales podemos sumar/restar\(360^{\circ}\). En este caso, nuestro ángulo es mayor que\(360^{\circ}\) por lo que tiene sentido restar\(360^{\circ}\) para obtener un ángulo coterminal positivo:\(595^{\circ}−360^{\circ}=235^{\circ}\). Ahora restar de nuevo para obtener un ángulo negativo:\(235^{\circ}−360^{\circ}=−125^{\circ}\).
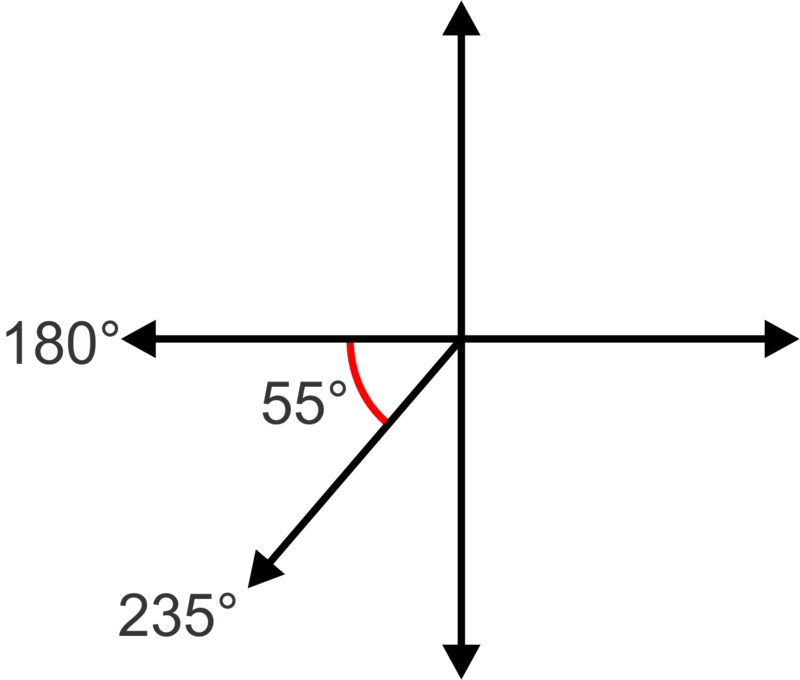
Al trazar cualquiera de estos ángulos podemos ver que el lado terminal se encuentra en el tercer cuadrante como se muestra.
Dado que el lado terminal se encuentra en el tercer cuadrante, necesitamos encontrar el ángulo entre\(180^{\circ}\) y\(235^{\circ}\), entonces\(235^{\circ}−180^{\circ}=55^{\circ}\).
Anteriormente, se le pidió encontrar el ángulo de referencia de\(−500^{\circ}\) y encontrar el cuadrante en el que se encuentra el lado terminal.
Solución
Dado que nuestro ángulo es de más de una rotación, necesitamos sumar\(360^{\circ}\) hasta que obtengamos un ángulo cuyo valor absoluto sea menor que\(360^{\circ}\):\(−500^{\circ}+360^{\circ}=−200^{\circ}\).
Si trazamos este ángulo vemos que es en\(−200^{\circ}\) sentido horario desde el origen o en sentido contrario a\(160^{\circ}\) las agujas del reloj. \(160^{\circ}\)yace en el segundo cuadrante.
Ahora determina el ángulo de referencia:\(180^{\circ}−160^{\circ}=20^{\circ}\).
Encuentra dos ángulos coterminales a\(138^{\circ}\), uno positivo y otro negativo.
Solución
\(138^{\circ}+360^{\circ}=498^{\circ}\)y\(138^{\circ}−360^{\circ}=−222^{\circ}\)
Encuentra el ángulo de referencia para\(895^{\circ}\).
Solución
\(895^{\circ}−360^{\circ}=535^{\circ}\),\(535^{\circ}−360^{\circ}=175^{\circ}\). El lado terminal se encuentra en el segundo cuadrante, por lo que necesitamos determinar el ángulo entre\(175^{\circ}\) y\(180^{\circ}\), que es\(5^{\circ}\).
Encuentra el ángulo de referencia para\(343^{\circ}\).
Solución
\(343^{\circ}\)está en el cuarto cuadrante por lo que necesitamos encontrar el ángulo entre\(343^{\circ}\) y\(360^{\circ}\) cuál es\(17^{\circ}\).
Revisar
Encuentra dos ángulos coterminales para cada medida de ángulo, uno positivo y otro negativo.
- \(−98^{\circ}\)
- \(475^{\circ}\)
- \(−210^{\circ}\)
- \(47^{\circ}\)
- \(−1022^{\circ}\)
- \(354^{\circ}\)
- \(−7^{\circ}\)
Determine el cuadrante en el que se encuentra el lado terminal y encuentre el ángulo de referencia para cada uno de los siguientes ángulos.
- \(102^{\circ}\)
- \(−400^{\circ}\)
- \(1307^{\circ}\)
- \(−820^{\circ}\)
- \(304^{\circ}\)
- \(251^{\circ}\)
- \(−348^{\circ}\)
- Explique por qué el ángulo de referencia para un ángulo entre\(0^{\circ}\) y\(90^{\circ}\) es igual a sí mismo.
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 13.5.