2.3.3: Ángulos de rotación en posiciones estándar

Última actualización
Guardar como PDF

Page ID: 107663

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ángulos en sentido antihorario que comienzan en el eje x positivo.

Mientras juegas un juego con amigos, estás usando un spinner. Sabes que el mejor número para aterrizar es el 7. El spinner se ve así:

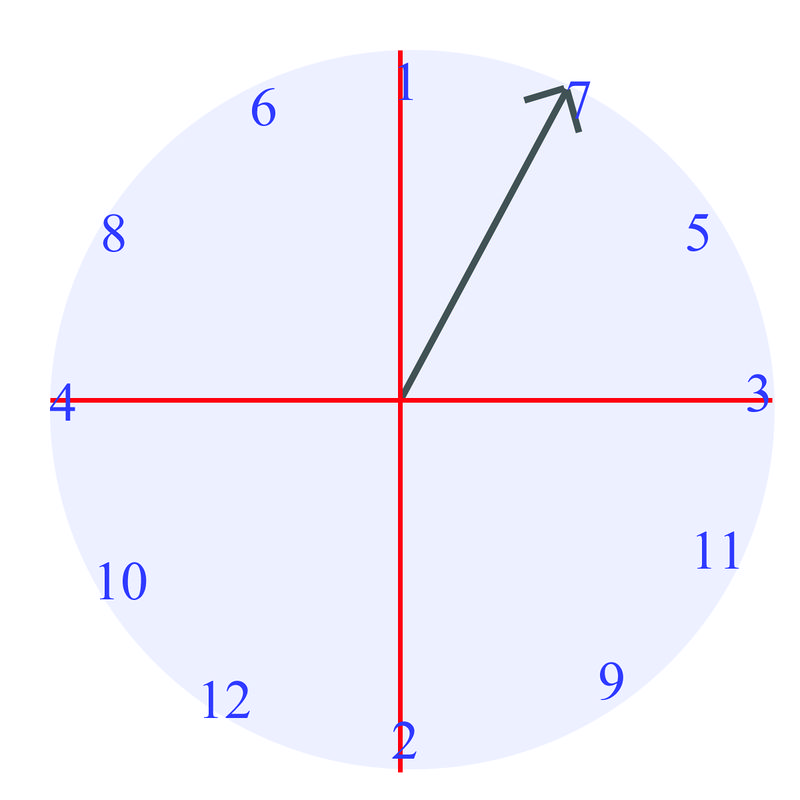
F-d_f7240c6d67dc4c11a91ef52a9bd37ee4fffeff6e8b3f1b75cad23ab6+image_tiny+image_tiny.jpg — Figura\(\PageIndex{1}\)

¿Se puede determinar cómo representar el ángulo del spinner si aterriza en el 7?

Ángulos de rotación en posiciones estándar

Considera nuestro juego que se juega con un spinner. Cuando haces girar el spinner, ¿hasta dónde ha llegado? Puedes responder a esta pregunta de varias maneras. Se podría decir algo así como “el spinner giró alrededor de 3 veces”. Esto significa que el spinner realizó 3 rotaciones completas, y luego aterrizó de nuevo donde comenzó.

También podemos medir la rotación en grados. En la lección anterior se trabajó con ángulos en triángulos, medidos en grados. Puede recordar de la geometría que una rotación completa es de 360 grados, generalmente escrita como\(360^{\circ}\). La mitad de una rotación es entonces\(180^{\circ}\) y un cuarto de rotación es\(90^{\circ}\). Cada una de estas mediciones será importante en este Concepto. Podemos usar nuestro conocimiento de graficar para representar cualquier ángulo. La siguiente figura muestra un ángulo en lo que se denomina posición estándar.

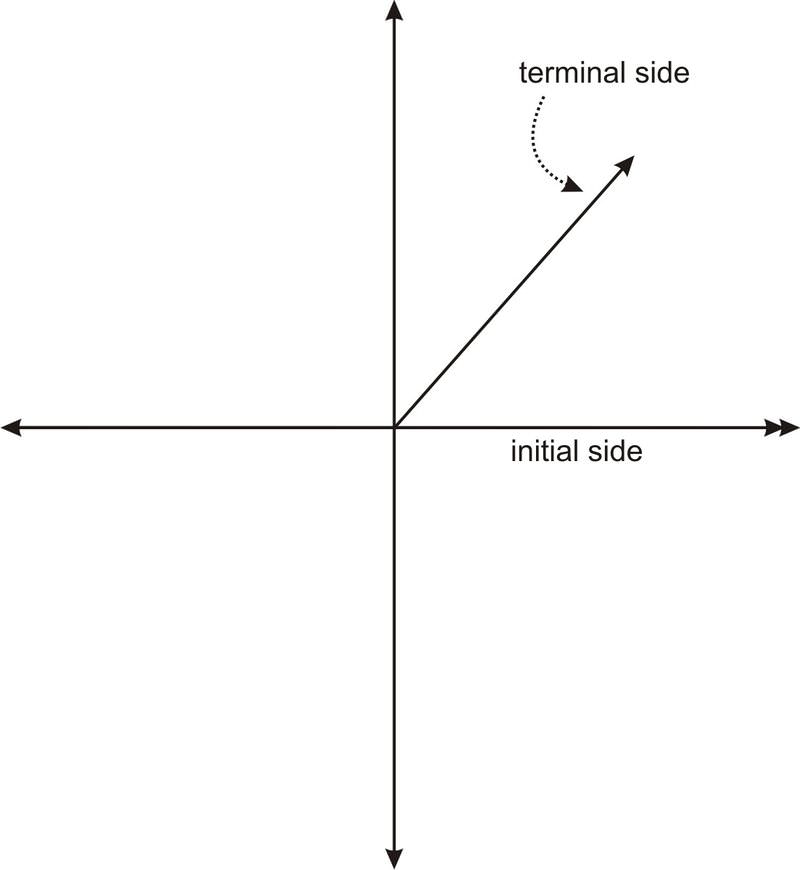
F-D_1072f225bd9d4a2d8cbb8338394f067fe366e9fe6281dd8c6b7bcbbf+image_tiny+image_tiny.jpg — Figura\(\PageIndex{2}\)

El lado inicial de un ángulo en posición estándar está siempre en el\(x\) eje −positivo. El lado terminal siempre se encuentra con el lado inicial en el origen. Observe que la rotación va en sentido contrario a las agujas del reloj. Esto significa que si giramos en el sentido de las agujas del reloj, generaremos un ángulo negativo. A continuación se presentan varios ejemplos de ángulos en posición estándar.

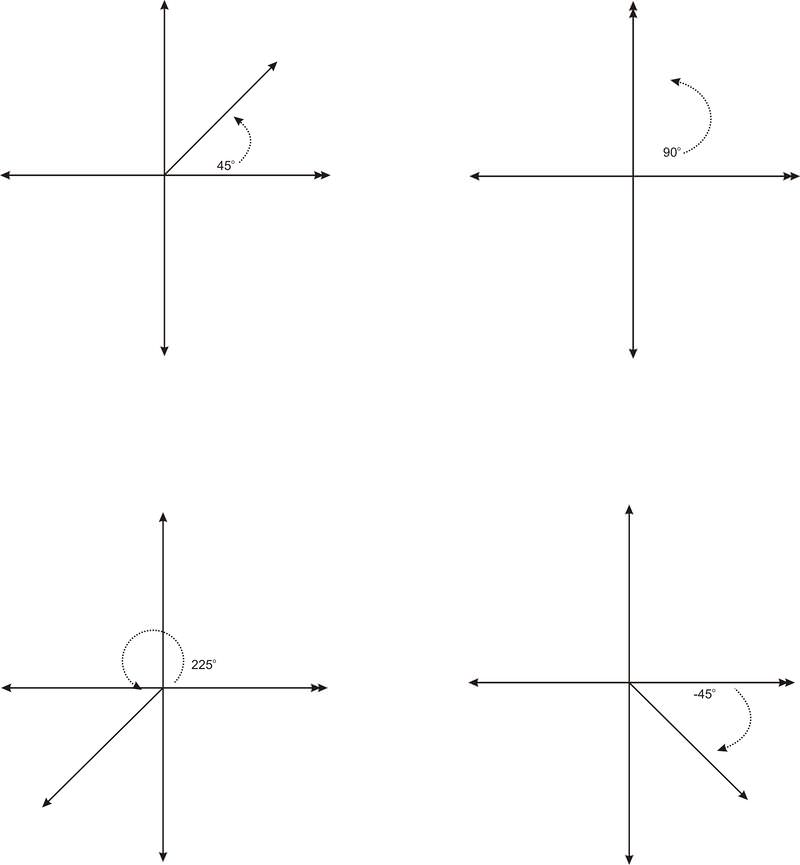
F-d_f8f5235b1723bd1976d35889a89c2a0b75358dd100a248a571d6443c+image_tiny+image_tiny.jpg — Figura\(\PageIndex{3}\)

El ángulo de 90 grados es uno de los cuatro ángulos cuadránticos. Un ángulo cuadrangular es aquel cuyo lado terminal se encuentra sobre un eje. Junto con\(90^{\circ}\),\(0^{\circ}\),\(180^{\circ}\) y\(270^{\circ}\) son ángulos cuadránticos.

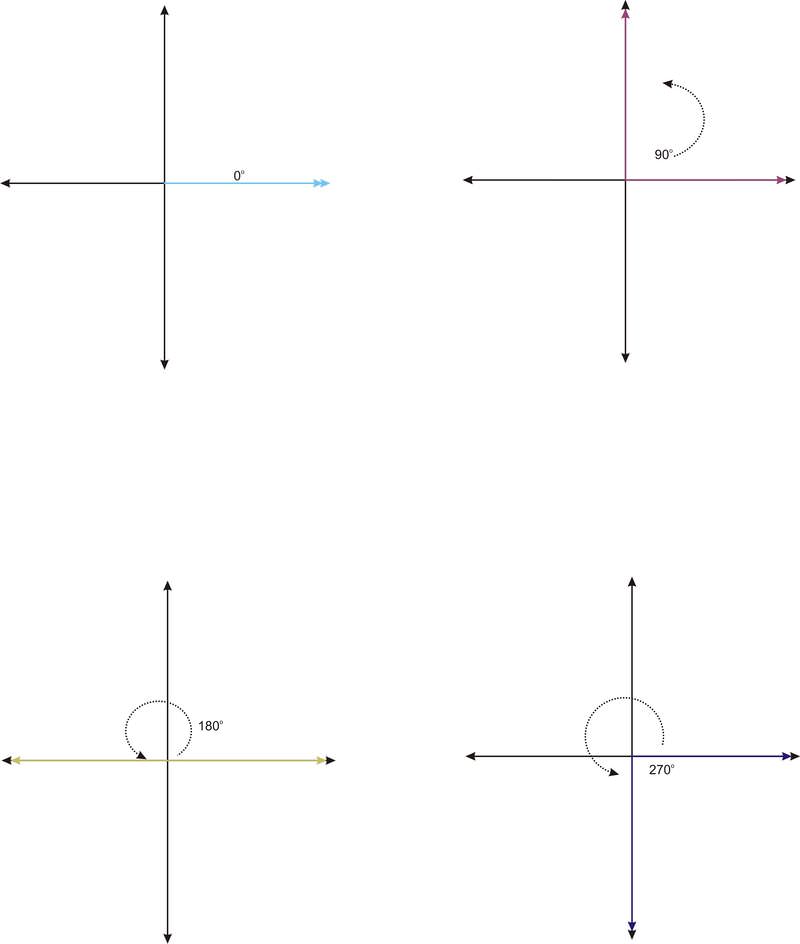
f-d_1d019d888fc8c48d0dfef9f7a1228f8bf2d3461180f2aa915edf91b3+image_tiny+image_tiny.jpg — Figura\(\PageIndex{4}\)

Estos ángulos son referidos como cuadránticos porque cada ángulo define un cuadrante. Observe que sin la flecha que indique la rotación,\(270^{\circ}\) parece como si se tratara de una\(−90^{\circ}\), definiendo el cuarto cuadrante. Observe también que se\(360^{\circ}\) vería igual\(0^{\circ}\).

Encontrar el ángulo de rotación

Identifica cuál es el ángulo en esta gráfica:

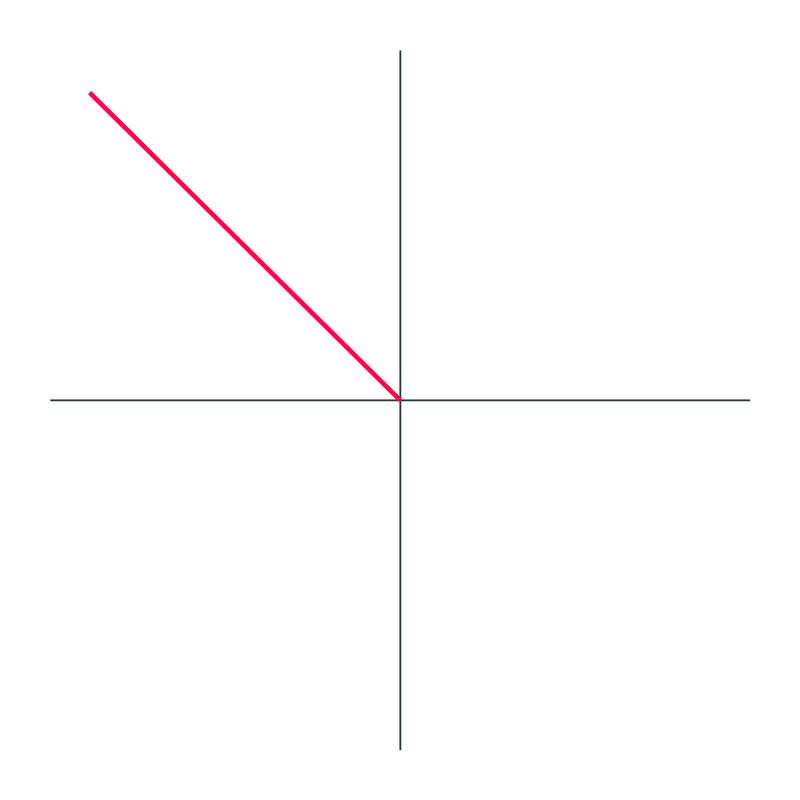
f-d_f7a195889e7de253660340b0f145fe63dfc9a1964dd107d56bce600a+image_tiny+image_tiny.jpg — Figura\(\PageIndex{5}\)

El ángulo dibujado es\(135^{\circ}\).

Identificar ángulos

Identificar los ángulos dentro de las siguientes gráficas.

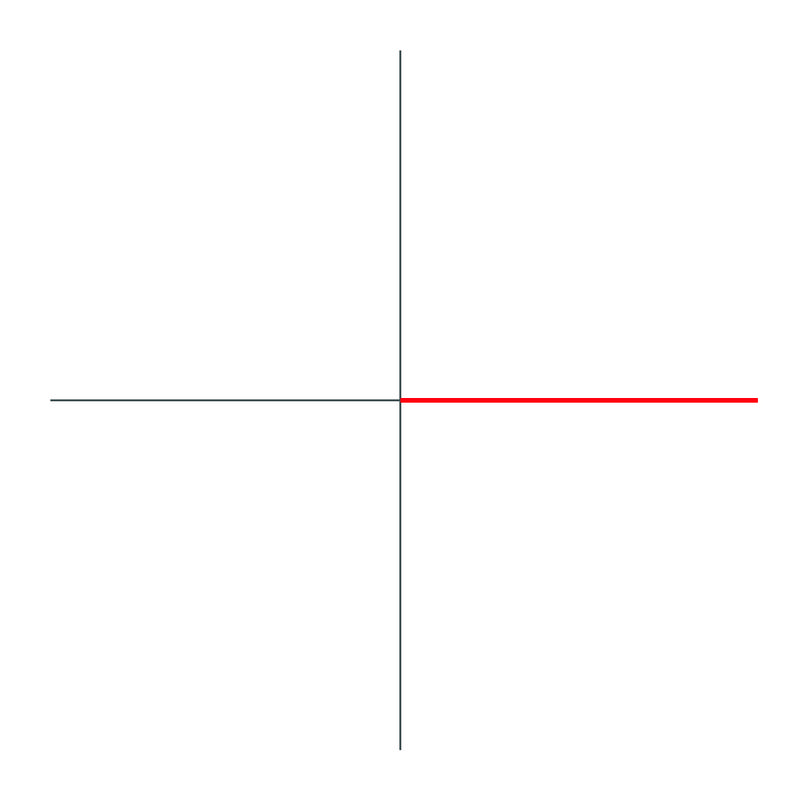
F-d_df5fbd81d6e8434c63320e3a56e91c66a684dc747aab49541acab0eb+image_tiny+image_tiny.jpg — Figura\(\PageIndex{6}\)

El ángulo dibujado es\(0^{\circ}\).

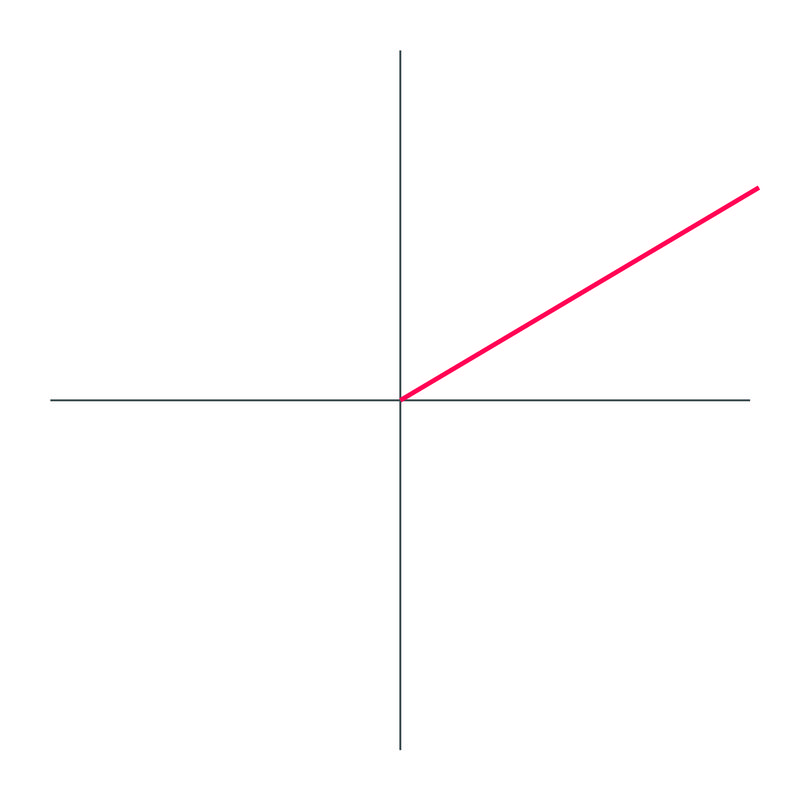
f-d_3fc211eaed01474fb3947bfddbee1d01d01574147ec21169e2c07f33+image_tiny+image_tiny.jpg — Figura\(\PageIndex{7}\)

El ángulo dibujado es\(30^{\circ}\)

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le pidió determinar cómo representar el ángulo del spinner si aterriza en el 7.

Solución

Ya que sabes que el ángulo entre las direcciones horizontal y vertical es\(90^{\circ}\), cada número en el spinner ocupa\(30^{\circ}\). Por lo tanto, ya que estás en el 7, sabes que eres 23 del camino a la vertical. Por lo tanto, el ángulo de la hilandera cuando aterriza en 7 es\(60^{\circ}\).

Ejemplo\(\PageIndex{2}\)

Identifica cuál es el ángulo en esta gráfica, usando ángulos negativos:

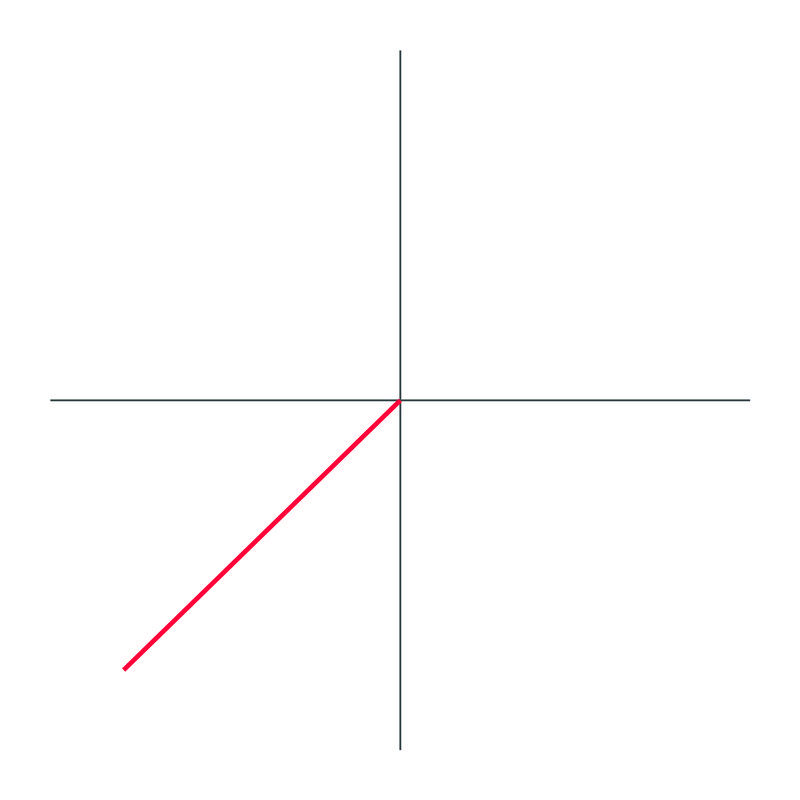
F-D_7610EAF8D5D27ebdfbe8e6212803cf034b85a5778fa12b3c7437e0bc+image_tiny+image_tiny.jpg — Figura\(\PageIndex{8}\)

Solución

El ángulo dibujado es\(−135^{\circ}\).

Ejemplo\(\PageIndex{3}\)

Identifica cuál es el ángulo en esta gráfica, usando ángulos negativos:

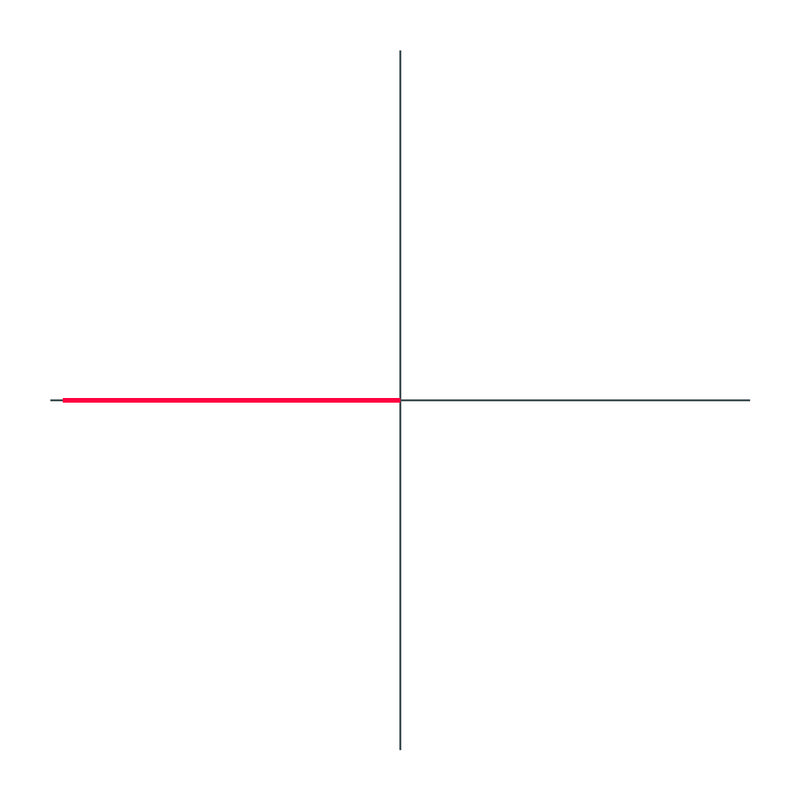
f-d_002af68eb1c0ebdd6c086e0f4611a8d0fae3fb979c39a39f3165cd46+image_tiny+image_tiny.jpg — Figura\(\PageIndex{9}\)

Solución

El ángulo dibujado es\(−180^{\circ}\).

Ejemplo\(\PageIndex{4}\)

Identifica cuál es el ángulo en esta gráfica, usando ángulos negativos:

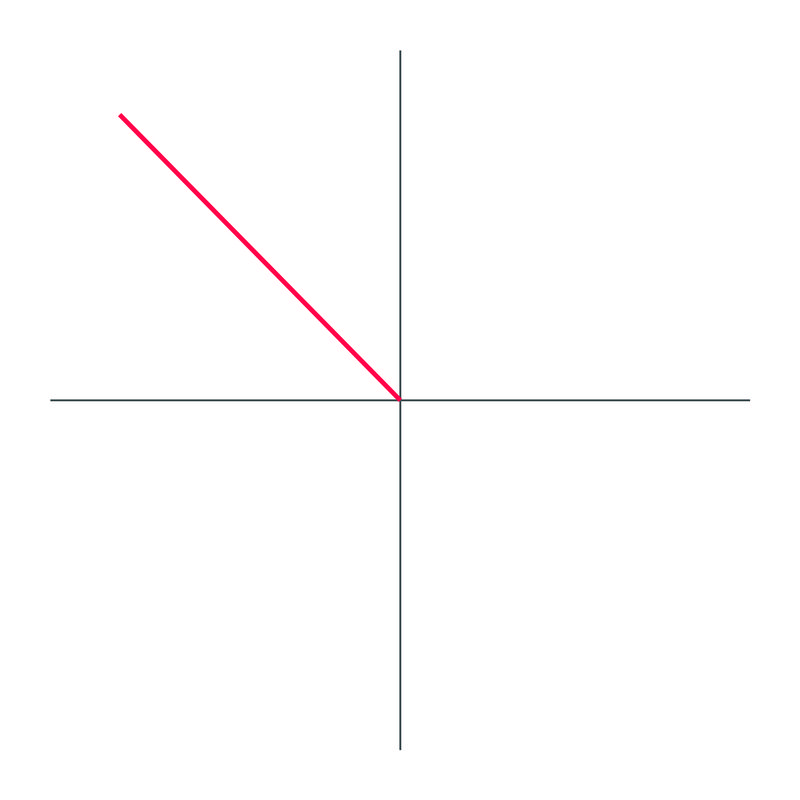
F-d_d355d95172d1e5f8855764619d1c5adbde379ef33f106f0fa453f9bd+image_tiny+image_tiny.jpg — Figura\(\PageIndex{10}\)

Solución

El ángulo dibujado es\(−225^{\circ}\).

Revisar

Dibuja un ángulo de\(90^{\circ}\).
Dibuja un ángulo de\(45^{\circ}\).
Dibuja un ángulo de\(−135^{\circ}\).
Dibuja un ángulo de\(−45^{\circ}\).
Dibuja un ángulo de\(−270^{\circ}\).
Dibuja un ángulo de\(315^{\circ}\).

Para cada diagrama, identifique el ángulo. Escribe el ángulo usando grados positivos.

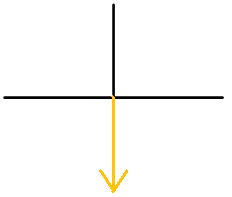
Figura\(\PageIndex{11}\)
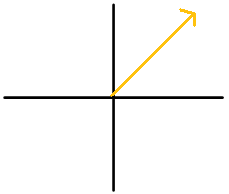
Figura\(\PageIndex{12}\)
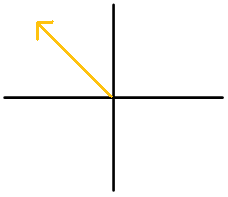
Figura\(\PageIndex{13}\)

Para cada diagrama, identifique el ángulo. Escribe el ángulo usando grados negativos.

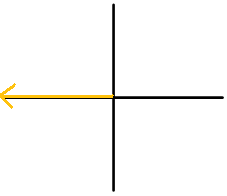
Figura\(\PageIndex{14}\)
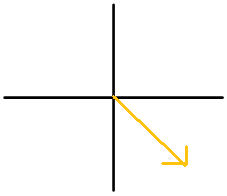
Figura\(\PageIndex{15}\)
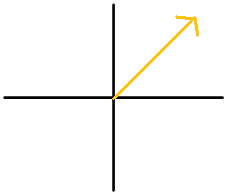
Figura\(\PageIndex{16}\)
Explica cómo convertir entre ángulos que usan grados positivos y ángulos que usan grados negativos.
¿En qué ángulo está el 7 en un reloj estándar de 12 horas? Usar grados positivos.
¿En qué ángulo está el 2 en un reloj estándar de 12 horas? Usar grados positivos.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.15.

El vocabulario

Término	Definición
Ángulo Cuadrantal	Un ángulo cuadrangular es un ángulo que tiene su lado terminal en una de las cuatro líneas de eje: positivo\(x\), negativo\(x\), positivo\(y\) o negativo\(y\).
Posición estándar	La posición estándar de un ángulo mide un ángulo que comienza desde el\(x\) eje positivo y va en sentido antihorario. Es el método típico para dibujar y medir un ángulo.

Recursos adicionales

Elemento interactivo

Video: Ángulos en posición estándar

Práctica: Ángulos de rotación en posiciones estándar