2.3.8: Funciones trigonométricas de ángulos negativos
- Page ID
- 107668
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ángulos medidos girando en sentido horario desde el\(x\) eje positivo.
Mientras practicas para el equipo de pista, regularmente te paras a considerar los valores de las funciones trigonométricas para el ángulo que has cubierto mientras corres por la pista circular en tu escuela. Hoy, sin embargo, es diferente. Para mantener las cosas más interesantes, tu entrenador ha decidido que tú y tus compañeros corran lo contrario de la dirección habitual en la pista. De tus estudios en la escuela, sabes que esto es el equivalente a un "ángulo negativo”.
Has corrido\(−45^{\circ}\) alrededor de la pista, y quieres precisar el valor de la función coseno para este ángulo. ¿Todavía es posible encontrar los valores de las funciones trigonométricas para estos nuevos tipos de ángulos?
Funciones trigonométricas de ángulos negativos
Recordemos que graficar un ángulo negativo significa girar en sentido horario. La gráfica a continuación muestra\(−30^{\circ}\).
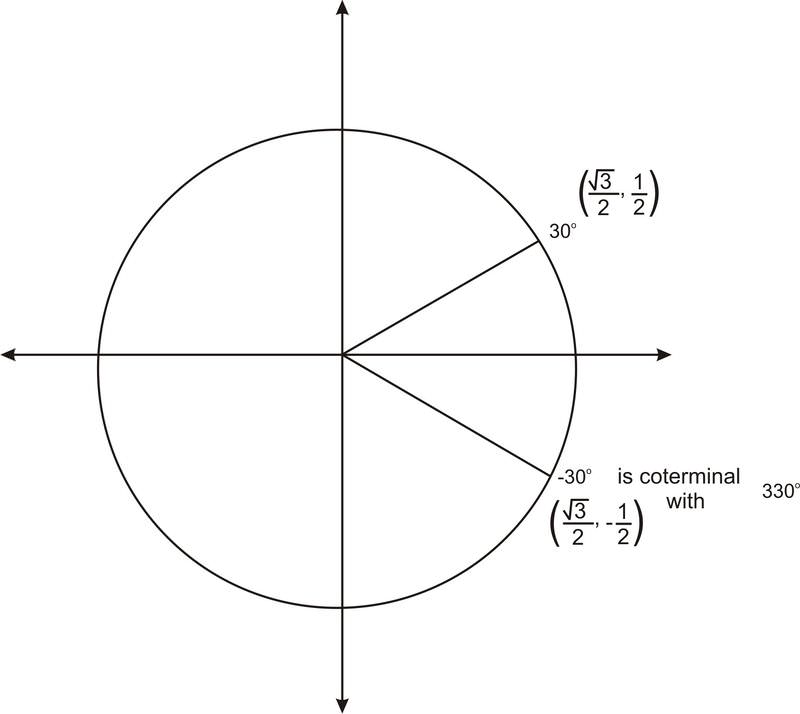
Observe que este ángulo es coterminal con\(330^{\circ}\). Entonces el par ordenado es\(\left(\dfrac{\sqrt{3}}{2},−\dfrac{1}{2} \right)\). Podemos usar este par ordenado para encontrar los valores de cualquiera de las funciones trigonométricas de\(−30^{\circ}\). Por ejemplo,\(\cos(−30^{\circ})=x=\dfrac{\sqrt{3}}{2}\).
En general, si un ángulo negativo tiene un ángulo de referencia de\(30^{\circ}\)\(45^{\circ}\), o\(60^{\circ}\), o si es un ángulo cuadrantal, podemos encontrar su par ordenado, y así podemos determinar los valores de cualquiera de las funciones trigonométricas del ángulo.
Encontrar el valor de las expresiones trigonométricas
Encuentra el valor de las siguientes expresiones:
1. \(\sin(−45^{\circ} )\)
\(\sin(−45^{\circ} )=−\dfrac{\sqrt{2}}{2}\)
\(−45^{\circ}\)está en el\(4^{th}\) cuadrante, y tiene un ángulo de referencia de\(45^{\circ}\). Es decir, este ángulo es coterminal con\(315^{\circ}\). Por lo tanto el par ordenado es\(\left(\dfrac{\sqrt{2}}{2},−\dfrac{\sqrt{2}}{2}\right)\) y el valor sinusoidal es\(−\dfrac{\sqrt{2}}{2}\).
2. \(\sec(−300^{\circ} )\)
\(\sec(−300^{\circ} )=2\)
El ángulo\(−300^{\circ}\) está en el\(1^{st}\) cuadrante y tiene un ángulo de referencia de\(60^{\circ}\). Es decir, este ángulo es coterminal con\(60^{\circ}\). Por lo tanto el par ordenado es\(\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\) y el valor secante es\(\dfrac{1}{x}=\dfrac{1}{\dfrac{1}{2}}=2\).
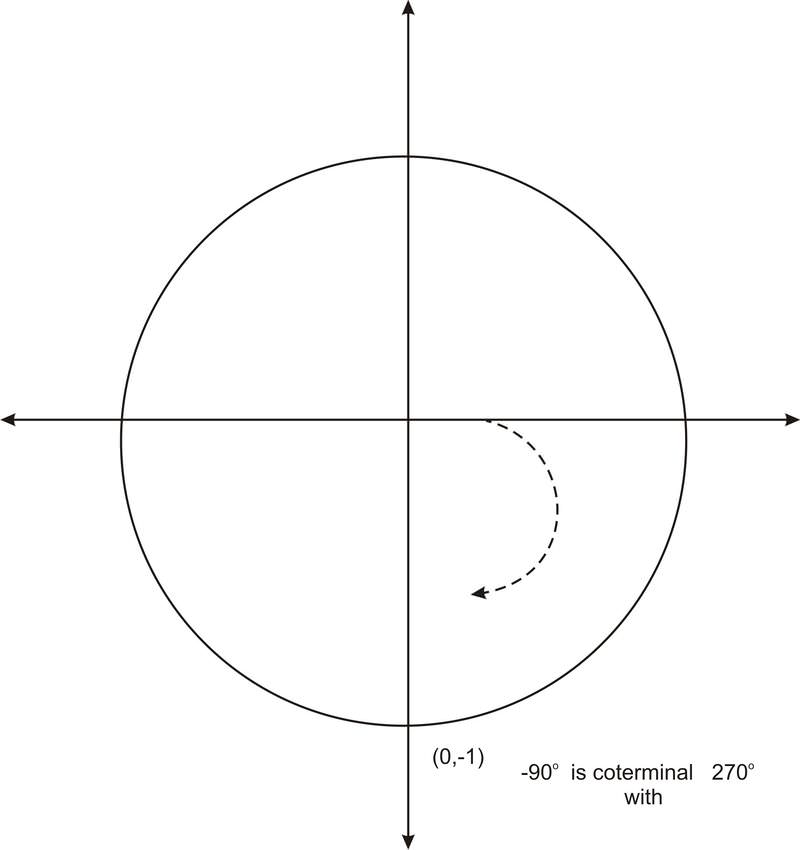
3. \(\cos(−90^{\circ} )\)
\(\cos(−90^{\circ} )=0\)
El ángulo −90^ {\ circ}\) es coterminal con\(270^{\circ}\). Por lo tanto, el par ordenado es (0, -1) y el valor del coseno es 0.
También podemos utilizar nuestro conocimiento de ángulos de referencia y pares ordenados para encontrar los valores de funciones trigonométricas de ángulos con medida mayor a 360 grados.
Anteriormente, se le preguntó si aún es posible encontrar los valores de las funciones trigonométricas para el nuevo tipo de ángulos.
Solución
Lo que quieres encontrar es el valor de la expresión:\(\cos(−45^{\circ})\)
\(\cos(−45^{\circ} )=\dfrac{\sqrt{2}}{2}\)
\(−45^{\circ}\)está en el\(4^{th}\) cuadrante, y tiene un ángulo de referencia de\(45^{\circ}\). Es decir, este ángulo es coterminal con\(315^{\circ}\). Por lo tanto el par ordenado es\(\left(\dfrac{\sqrt{2}}{2},−\dfrac{\sqrt{2}}{2}\right)\) y el valor coseno es\(\dfrac{\sqrt{2}}{2}\).
Encuentra el valor de la expresión:\(\cos −180^{\circ}\)
Solución
El ángulo\(−180^{\circ}\) es coterminal con\(180^{\circ}\). Por lo tanto el par ordenado de puntos es\((-1, 0)\). El coseno es la coordenada “x”, así que aquí está -1.
Encuentra el valor de la expresión:\(\sin−90^{\circ}\)
Solución
El ángulo\(−90^{\circ}\) es coterminal con\(270^{\circ}\). Por lo tanto el par ordenado de puntos es\((0, -1)\). El seno es el "\(y\)" "coordinte, entonces aquí está -1.
Encuentra el valor de la expresión:\(\tan −270^{\circ}\)
Solución
El ángulo\(−270^{\circ}\) es coterminal con\(90^{\circ}\). Por lo tanto el par ordenado de puntos es\((0, 1)\). La tangente es la coordenada\(y\) "" dividida por la coordenada\(x\) "”. Dado que la coordenada\(x\) "" es 0, la tangente es indefinida.
Revisar
Calcular cada valor.
- \(\sin −120^{\circ}\)
- \(\cos −120^{\circ}\)
- \(\tan −120^{\circ}\)
- \(\csc −120^{\circ}\)
- \(\sec −120^{\circ}\)
- \(\cot −120^{\circ}\)
- \(\csc −45^{\circ}\)
- \(\sec −45^{\circ}\)
- \(\tan −45^{\circ}\)
- \(\cos −135^{\circ}\)
- \(\csc −135^{\circ}\)
- \(\sec −135^{\circ}\)
- \(\tan −210^{\circ}\)
- \(\sin −270^{\circ}\)
- \(\cot −90^{\circ}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.19.
vocabulario
| Término | Definición |
|---|---|
| Ángulo Negativo | Un ángulo negativo es un ángulo medido girando en sentido horario (en lugar de antihorario) desde el\(x\) eje positivo. |
Recursos adicionales
Video: Evaluación de funciones trigonométricas de cualquier ángulo - Descripción general

