2.5.8: Longitud de un Acorde
- Page ID
- 107693
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dos veces el radio por el seno de la mitad del ángulo en radianes.
Se te ha pedido que ayudes a los alumnos más jóvenes de tu escuela con su clase de Educación Física. Mientras trabaja una tarde, se le pide que saque un paracaídas con el que puedan jugar los alumnos. Mientras los alumnos están jugando, uno de ellos camina por una pequeña porción del paracaídas en lugar de debajo de él como se supone que debe hacerlo. Si el paracaídas tiene la forma de un círculo con un radio de 6 metros, y el camino que el estudiante recorrió por el conducto cubrió un ángulo de\(50^{\circ}\), ¿cuál es la longitud del camino que recorrió a través del paracaídas?
Tal vez recuerde de sus estudios de Geometría que un acorde es un segmento que comienza y termina en un círculo.
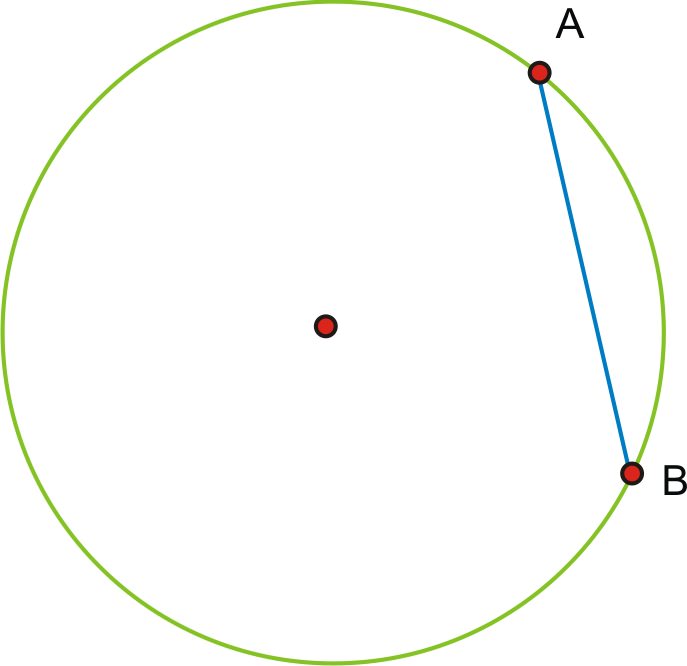
\(\overline{AB}\)es un acorde en el círculo.
Podemos calcular la longitud de cualquier acorde si conocemos la medida del ángulo y la longitud del radio. Debido a que cada punto final de la cuerda está en el círculo, la distancia desde el centro a A y B es la misma que la longitud del radio.
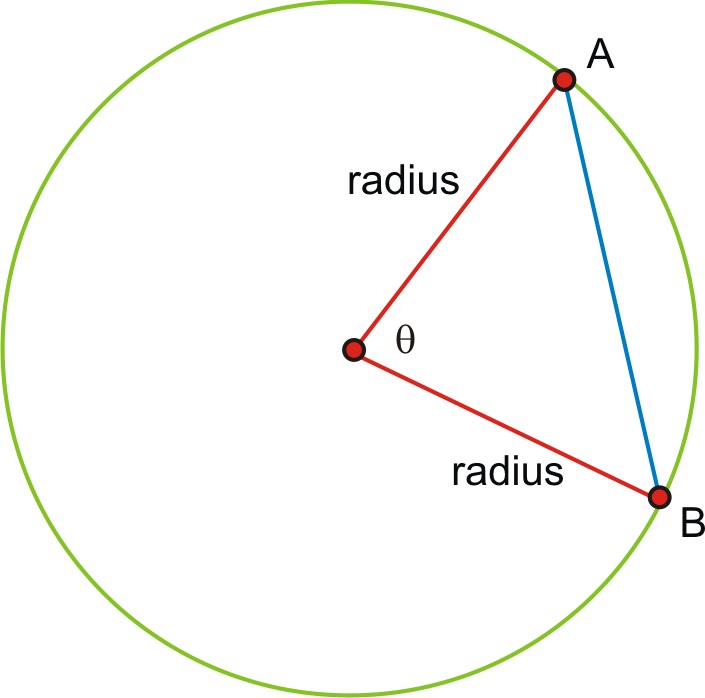
A continuación, si biseccionamos el ángulo, el ángulo bisectriz debe ser perpendicular a la cuerda y lo biseccionamos (dejaremos la prueba de esto a tu clase de Geometría). Esto forma un triángulo rectángulo.
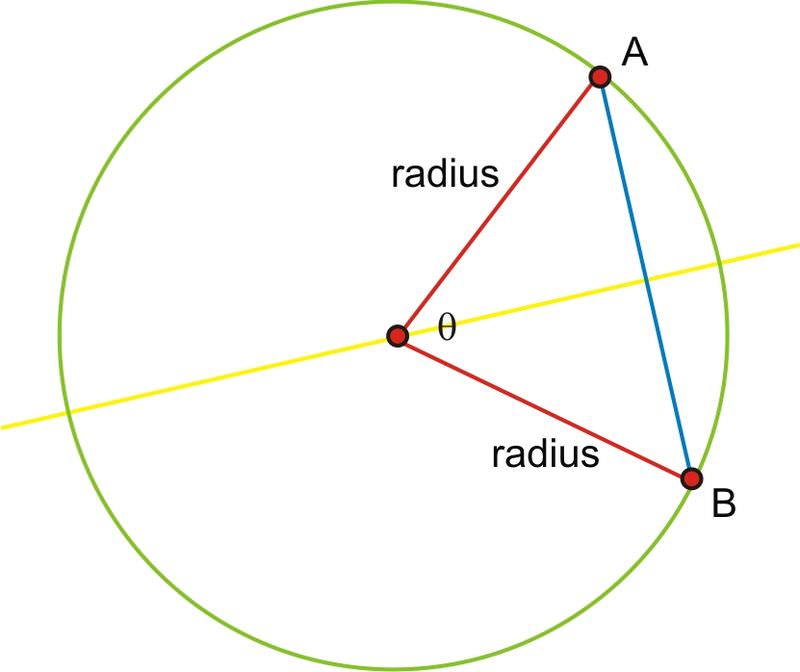
Ahora podemos usar una relación sinusoidal simple para encontrar la mitad del acorde, llamado c aquí, y duplicar el resultado para encontrar la longitud del acorde.
\(\begin{aligned} \sin\dfrac{\theta}{2}&=\dfrac{c}{r} \\ c&=r\times \sin\dfrac{\theta}{2}\end{aligned}\)
Entonces la longitud del acorde es:
\(2c=2r \sin\dfrac{\theta}{2}\)
Encontrar la longitud de un acorde
1. Encuentra la longitud de la cuerda de un círculo con radio de 8 cm y un ángulo central de\(110^{\circ}\). Aproxime su respuesta al mm más cercano.
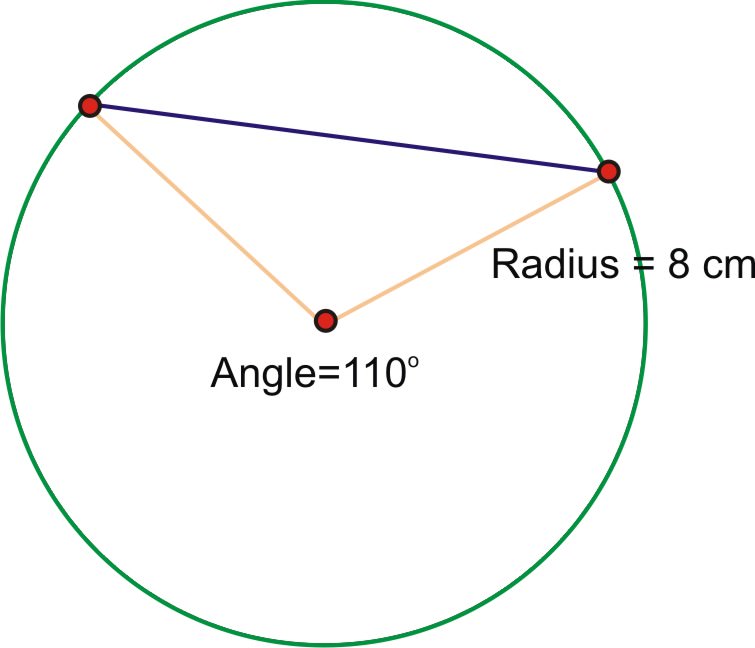
Primero debemos convertir la medida del ángulo a radianes:
\(110\times \dfrac{\pi }{180}=\dfrac{11\pi }{18}\)
Usando la fórmula, la mitad de la longitud de la cuerda debe ser el radio del círculo multiplicado por el seno de la mitad del ángulo.
\(\begin{aligned} \dfrac{11\pi }{18}\times \dfrac{1}{2}=\dfrac{11\pi }{36} \\ 8\times \sin \dfrac{11\pi }{36} \end{aligned}\)
Multiplica este resultado por 2.
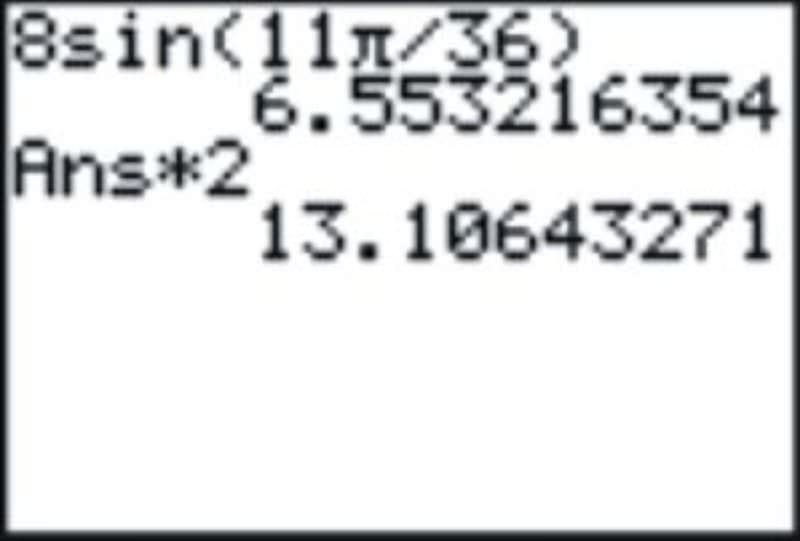
Entonces, la longitud del acorde es de aproximadamente 13.1 cm.
2. Encuentra la longitud de la cuerda de un círculo con un radio de 2 m que tiene un ángulo central de\(90^{\circ}\).
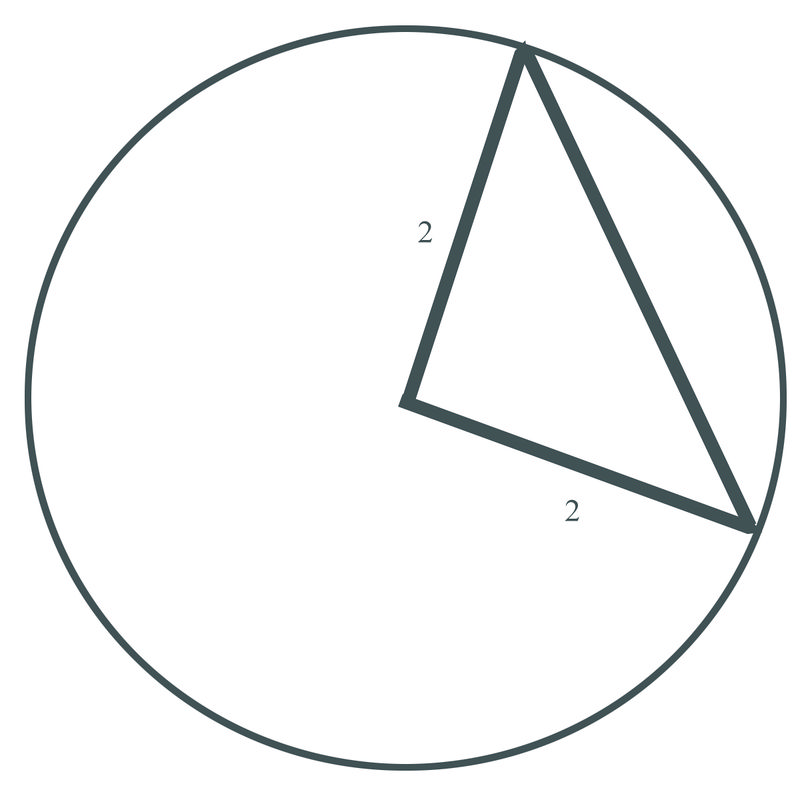
Primero convierte el ángulo a radianes:
\(90\times \dfrac{\pi }{180}=\dfrac{\pi }{2}\)
Usando la fórmula, la mitad de la longitud de la cuerda debe ser el radio del círculo multiplicado por el seno de la mitad del ángulo.
\(\dfrac{\pi }{2}\times \dfrac{1}{2}=\dfrac{\pi }{4} \\ 2\times \sin \dfrac{\pi }{4}\)
Multiplica este resultado por 2.
Por lo que la respuesta es aproximadamente de 2.83 metros.
3. Encuentra la longitud de la cuerda de un círculo con radio de 1 m y un ángulo central de\(170^{\circ}\).
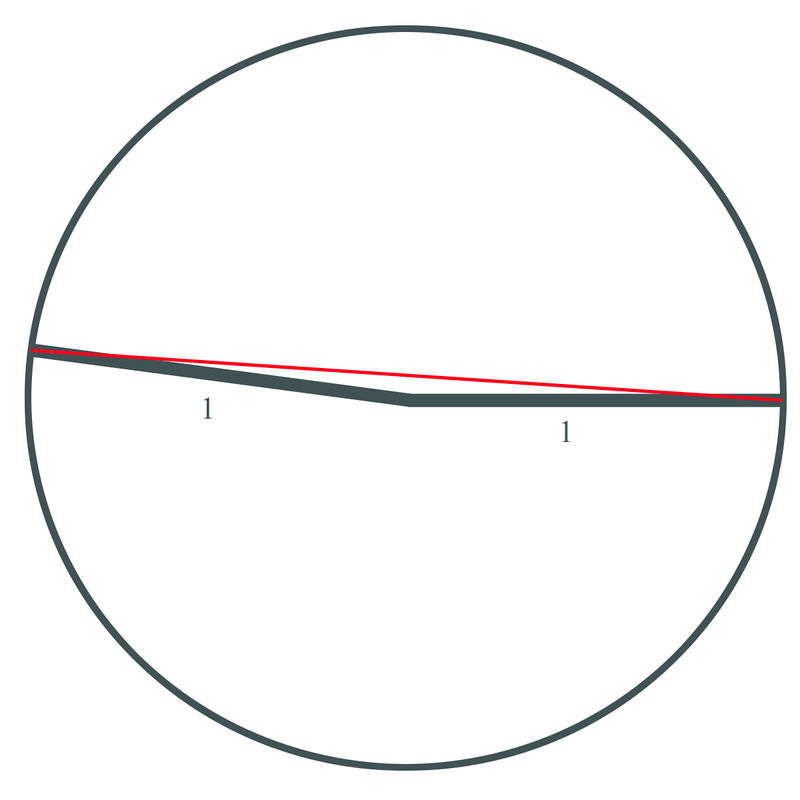
Primero debemos convertir la medida del ángulo a radianes:
\(170\times \dfrac{\pi }{180}=\dfrac{17\pi }{18}\)
Usando la fórmula, la mitad de la longitud de la cuerda debe ser el radio del círculo multiplicado por el seno de la mitad del ángulo.
\(\begin{aligned} \dfrac{17\pi }{18} \times \dfrac{1}{2}&= \dfrac{17\pi }{36} \\1\times \sin \dfrac{17\pi }{36}&=.996\end{aligned}\)
Multiplica este resultado por 2.
Entonces, la longitud del arco es aproximadamente 1.992
Observe que la longitud de la cuerda es de casi 2 metros, que sería el diámetro del círculo. Si el ángulo hubiera sido de 180 grados, la cuerda habría sido simplemente la distancia a través del círculo pasando por el medio, que es el diámetro.
Anteriormente, se le preguntó cuál es la longitud del camino que ella caminó a través del paracaídas.
Solución
Con la ecuación para la longitud de un acorde en la mano, se puede calcular la distancia que el estudiante corrió a través del paracaídas:
Primero convierte la medida en grados a radianes:
\(50\times \dfrac{\pi }{180} \approx .27\pi\)
\(2r \sin \dfrac{\theta}{2}=(2)(6)\sin \dfrac{.27\pi }{2}=12 \sin.135\pi \approx 4.94 \text{ meters}\)
Si corres un trozo de cuerda a través de una dona que estás comiendo, y el radio entre los extremos de la cuerda y el centro de la dona es de 4 pulgadas, ¿cuánto dura la cuerda si es el ángulo barrido por la cuerda\(20^{\circ}\)?
Solución
Puedes usar la ecuación\(C=2r\sin\left(\dfrac{\theta}{2}\right)\) para resolver este problema: (No olvides convertir ángulos a radianes)
\(\begin{aligned} C&=2r\sin \left(\dfrac{\theta}{2}\right) \\ C&=(2)(4)\sin\left(\dfrac{.349}{2}\right) \\ C&=8(.1736) \\ C&=1.388 \text{ inches}\end{aligned}\)
Estás cenando una noche con tu familia en el restaurante italiano local. Un trozo de espagueti hace un acorde en tu plato. Sabes que la longitud del hilo de espagueti es de 5 pulgadas, y el radio del plato es de 7 pulgadas. ¿Cuál es el ángulo barrido por el acorde?
Solución
Dado que se conocen el radio de la placa y la longitud de la cuerda, se puede resolver para el ángulo:
\ (\ comenzar {alineado}
C&=2 r\ sin\ izquierda (\ dfrac {\ theta} {2}\ derecha)\
\ dfrac {C} {2 r} &=\ sin\ izquierda (\ dfrac {\ theta} {2}\ derecha)\
\ sin ^ {-1}\ izquierda (\ dfrac {c} {2 r}\ derecha) &=\ dfrac {\ theta} {2}\\
\ sin ^ {-1}\ izquierda (\ dfrac {5} {14}\ derecha) &=\ dfrac {\ theta} {2}\\
.365&=\ dfrac {\ theta} {2}\\
\ theta&=.73
\ end {alineado}\)
El ángulo abarcado por los espaguetis es de .73 radianes.
Si dibujas un acorde a través de un círculo y haces un acorde a través de él que tiene una longitud de 15 pulgadas, barriendo un ángulo de\(\pi \) radianes, ¿cuál es el radio del círculo que dibujaste?
Solución
Usando la ecuación para la longitud de un acorde:
\(\begin{aligned} c&=2r \sin(\dfrac{\theta }{2}) \\ 15&=(2r)\sin(\dfrac{\pi }{2}) \\ r&=7.5 \end{aligned}\)
Como puede ver, el radio del círculo es de 7.5 pulgadas. Esto es lo que debes esperar, ya que el acorde barre un ángulo de\(\pi \). Esto significa que barre la mitad del círculo, de modo que el acorde en realidad va a través de todo el diámetro del círculo. Entonces, si el acorde va a través del diámetro y tiene una longitud de 15 pulgadas, entonces el radio del círculo debe ser de 7.5 pulgadas.
Revisar
- Encuentra la longitud de la cuerda de un círculo con radio de 1 m y un ángulo central de\(100^{\circ}\).
- Encuentra la longitud de la cuerda de un círculo con radio de 8 km y un ángulo central de\(130^{\circ}\).
- Encuentra la longitud de la cuerda de un círculo con radio de 4 pulgadas y un ángulo central de\(45^{\circ}\).
- Encuentra la longitud de la cuerda de un círculo con radio 3 pies y un ángulo central de\(32^{\circ}\).
- Encuentra la longitud de la cuerda de un círculo con radio de 2 cm y un ángulo central de\(112^{\circ}\).
- Encuentra la longitud de la cuerda de un círculo con radio de 7 pulgadas y un ángulo central de\(135^{\circ}\).
Resuelve la variable que falta en cada círculo.
-
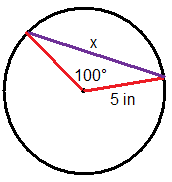
Figura\(\PageIndex{8}\) -
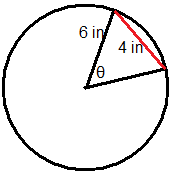
Figura\(\PageIndex{9}\) -
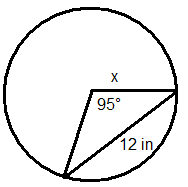
Figura\(\PageIndex{10}\) -
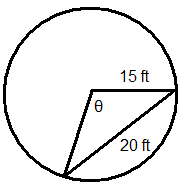
Figura\(\PageIndex{11}\) -
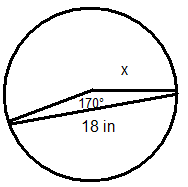
Figura\(\PageIndex{12}\) -
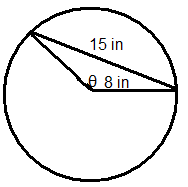
Figura\(\PageIndex{13}\)
Utilice la imagen de abajo para las preguntas 13-15.
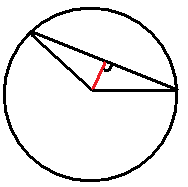
- Supongamos que conocía la longitud del acorde, la longitud del radio y el ángulo central del círculo anterior. Describir una manera de encontrar la longitud del segmento rojo usando el Teorema de Pitágoras.
- Supongamos que conocía la longitud del acorde, la longitud del radio y el ángulo central del círculo anterior. Describir una manera de encontrar la longitud del segmento rojo usando coseno.
- ¿Qué necesitarías saber para encontrar el área del segmento (la porción del círculo entre el acorde y el borde del círculo)? Describir cómo encontrar la zona de esta región.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.7.
El vocabulario
| Término | Definición |
|---|---|
| Acorde | Un acorde es una línea recta a través de un círculo, que cruza el círculo en dos lugares, pero no pasa por el centro del círculo. |

