2.5.7: Área de un Sector
- Page ID
- 107687
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La mitad del radio cuadrado multiplicado por el ángulo en radianes.
Mientras almuerzas con tus amigos algún día decides conseguir un poco de pastel. La cafetería de la escuela tiene una venta de pasteles si compras el pastel entero en lugar de una rebanada individual. Ya que tú y tus amigos planean comerse el pastel entero de todos modos, estás feliz de hacer la compra.
Tú decides cortarte una pieza. Cuando has sacado tu sección de pastel, uno de tus amigos objetos que has recortado más de lo que te corresponde. Si el radio del pastel es de seis pulgadas, y el ángulo formado por el extremo de la cuña de tu pastel es\(30^{\circ}\), ¿cuál es el área de tu pieza de pastel? ¿Es más que tu parte justa si hay cinco personas (incluyéndolo a ti) dividiendo el pastel?
Área de un Sector
Una de las fórmulas geométricas más comunes es el área de un círculo:
\(A=\pi r^2\)
En términos de rotación angular, esta es el área creada por\(2\pi \) radianes.
\(2\pi \text{ rad}=\pi r^2 \text{ area}\)
Un semicírculo, o rotación de\(\pi \) radianes crearía una sección, o sector del círculo igual a la mitad del área o:
\(\dfrac{1}{2} \pi r^2\)
Entonces un ángulo de 1 radián definiría un área de un sector igual a:
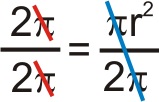
\(1=\dfrac{1}{2}r^2\)
A partir de esto podemos determinar el área del sector creada por cualquier ángulo,\(\theta \) radianes, para ser:
\(A=\dfrac{1}{2}r^2\theta\)
Encontrar el Área
1. Los cultivos a menudo se cultivan utilizando una técnica llamada riego de pivote central que da como resultado campos de forma circular.

Aquí una imagen satelital tomada sobre campos en Kansas que utilizan este tipo de sistema de riego.

Si la tubería de riego tiene 450 m de longitud, ¿cuál es el área que se puede regar después de una rotación de\(\dfrac{2\pi }{3}\) radianes?
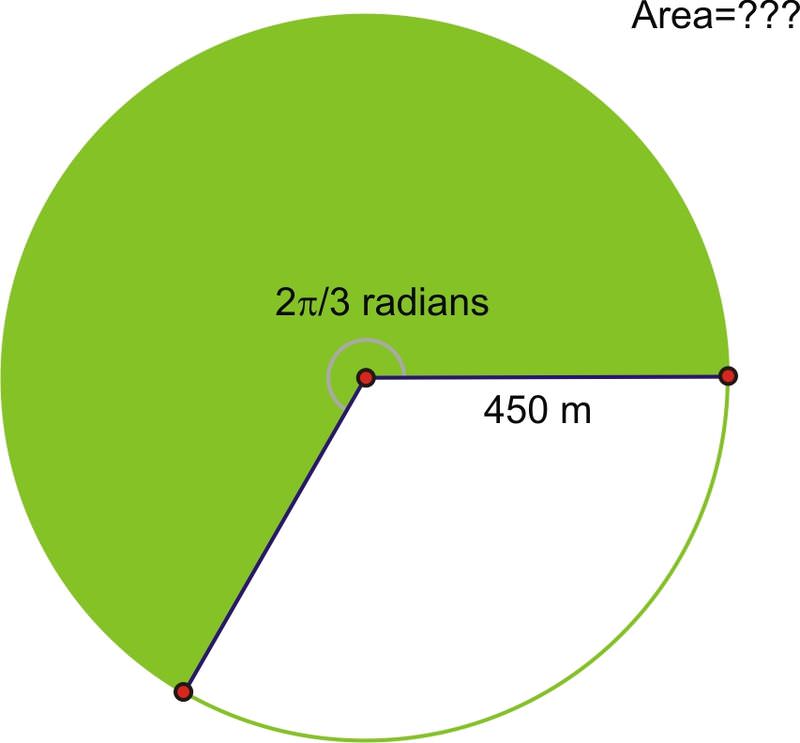
Usando la fórmula:
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ A&=\dfrac{1}{2}(450)^2\left(\dfrac{2\pi }{3}\right)\end{aligned}\)

El área es de aproximadamente 212,058 metros cuadrados.
2. Una rosquilla tiene un agujero en el medio con un radio de 1 cm, y la distancia desde el centro del orificio hasta el borde exterior de la rosquilla es de 3 cm. ¿Cuál es la superficie de un sector de 14 de la rosquilla?

La fórmula para el área de un sector es\(A=\dfrac{1}{2}r^2\theta \). El uso de esta fórmula para encontrar el área del sector desde el centro hacia afuera da:
\(\begin{aligned} A &=\dfrac{1}{2}r^2 \theta \\ A &=\dfrac{1}{2}3^2 \dfrac{\pi }{2}\\ A&=\dfrac{9\pi }{4} \end{aligned}\)
Ahora es necesario restar el área del sector que forma parte del agujero, y por lo tanto no parte de la rosquilla:
\(\begin{aligned} A &= \dfrac{1}{2}r^2 \theta \\ A &=\dfrac{1}{2} (1)^2 \dfrac{\pi }{2}\\ A&=\pi 4 \end{aligned}\)
Área del sector de donas:\(A=\dfrac{9\pi }{4}−\dfrac{\pi }{4}=\dfrac{8\pi }{4}=2\pi\)
3. Un conductor recorre una vía circular que tiene un radio de 70 metros. Si el ángulo desde la línea de salida hasta su posición actual es\(\dfrac{\pi }{3}\) radianes, ¿cuál es el área del sector trazada por su automóvil?

El área de un sector es:\(A=\dfrac{1}{2}r^2\theta \). Esto nos lleva a:
\(\begin{aligned} A &=\dfrac{1}{2}r^2\theta \\ A &=\dfrac{1}{2}(70)^2 \dfrac{\pi }{3}\\ A&\approx 73.3 \text{ meters} \end{aligned}\)
Antes, te preguntaron cuál es el área de tu pieza de pastel.
Solución
Ahora sabes que la ecuación para el área de un círculo barrida por algún ángulo es:
\(A=\dfrac{1}{2}r^2\theta\)
Aplicando esto a tu rebanada de pastel, tienes un área de:
\(A=\dfrac{1}{2}\times 62\times \dfrac{\pi }{6}=3\pi \)
Y el área total del pastel es:
\(\pi r^2=36\pi\)
Para saber cuál es tu porción justa del pastel, multiplica el área total por tu fracción:
\(\dfrac{1}{5} \times 36\pi =7.2\pi\)
Y como la pieza que tomaste es de solo 3\ pi de tamaño, ¡definitivamente no estás tomando demasiado!
Si el radio de un sector es de 5 pies, y el sector barre un ángulo de\(43^{\circ}\), encuentra el área del sector.
Solución
Ya que sabes eso\(A=\dfrac{1}{2}r^2\theta \), puedes resolver para el área (no olvides convertir los grados del ángulo a radianes):
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ A&=\dfrac{1}{2} (25)(.75) \\ A&=9.375 \end{aligned}\)
Si una cuña para tarta tiene un área de 15 cuadrados en pulgadas, y el pastel tiene un radio de 9 pulgadas, encuentre el ángulo barrido por el sector.
Solución
Ya que sabes eso\(A=\dfrac{1}{2}r^2\theta \), puedes resolver para el ángulo barrido por el sector (no olvides que el ángulo se medirá en radianes):
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ 15&=\dfrac{1}{2} (81)(\theta ) \\ \theta &=\dfrac{(2)(15)}{81} \\ \theta &=.37 \end{aligned}\)
Si tienes un trozo de pastel redondo que tiene un área de 20 pulgadas cuadradas, y sabes que la pieza barre un ángulo de\(25^{\circ}\), encuentra el radio del pastel.
Solución
Ya que sabes eso\(A=\dfrac{1}{2}r^2\theta \), puedes resolver para el radio del pastel (no olvides convertir los grados del ángulo a radianes):
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ 20&=\dfrac{1}{2}(r^2)(.436) \\ r^2&=\dfrac{(2)(20)}{.436 }\\ r^2&=91.743 \\ r&=9.58 \end{aligned}\)
Revisar
- Si el radio de un sector es de 8 pulgadas, y el ángulo central del sector es\(40^{\circ}\), encuentra el área del sector.
- Si el radio de un sector es de 12 pulgadas, y el ángulo central del sector es\(\dfrac{\pi }{6}\) radianes, encuentra el área del sector.
- Si el radio de un sector es de 6 pulgadas, y el ángulo central del sector es\(140^{\circ}\), encuentra el área del sector.
- Si el radio de un sector es de 5 pulgadas, y el ángulo central del sector es\(\dfrac{5\pi }{3}\) radianes, encuentra el área del sector.
- Si el radio de un sector es de 10 pulgadas, y el ángulo central del sector es\(100^{\circ}\), encuentra el área del sector.
- Si una cuña para tarta tiene un área de 10 pulgadas cuadradas, y la tarta tiene un radio de 6 pulgadas, encuentra el ángulo barrido por el sector.
- Si una cuña para tarta tiene un área de 15 pulgadas cuadradas, y la tarta tiene un radio de 4 pulgadas, encuentra el ángulo barrido por el sector.
- Si una cuña para tarta tiene un área de 12 pulgadas cuadradas, y la tarta tiene un radio de 3 pulgadas, encuentra el ángulo barrido por el sector.
- Si tienes un trozo de pastel redondo que tiene un área de 20 pulgadas cuadradas, y sabes que la pieza barre un ángulo de\(\dfrac{\pi }{3}\) radianes, encuentra el radio del pastel.
- Si tienes un trozo de pastel redondo que tiene un área de 100 pulgadas cuadradas, y sabes que la pieza barre un ángulo de\(50^{\circ}\), encuentra el radio del pastel.
- Si tienes un trozo de pastel redondo que tiene un área de 35 pulgadas cuadradas, y sabes que la pieza barre un ángulo de\(\dfrac{2\pi }{5}\) radianes, encuentra el radio del pastel.
- Si tienes un trozo de pastel redondo que tiene un área de 20 pulgadas cuadradas, y sabes que la pieza barre un ángulo de\(30^{\circ}\), encuentra el radio del pastel.
Una pizza tiene un radio de 10 pulgadas. Utilice esta información para responder a las preguntas 13-15.
- Se retira una rebanada. La longitud de la corteza de la rebanada faltante es de 3 pulgadas. ¿Cuál es el área de la porción faltante?
- Comes tres piezas con un ángulo central de\(\dfrac{4\pi }{5}\). ¿Cuál es la zona de la pizza que comiste?
- Una pizza grande tiene un radio de 12 pulgadas. ¿Cuál es el área de la mitad de la pizza grande?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.6.
El vocabulario
| Término | Definición |
|---|---|
| Sector | Un sector de un círculo es una porción de un círculo contenida entre dos radios del círculo. Los sectores se pueden medir en grados. |

