2.6.1: Gráfica sinusoidal y gráfica de coseno
- Page ID
- 107603
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Funciones de trazo gráfico y estiramiento
Tu misión, en caso de que decidas aceptarla, ya que Trigonometría de Agente es graficar la función\(y=2\cos x\). ¿Cuáles son los mínimos y máximos de tu gráfica?
Graficando Seno y Coseno
En este concepto, tomaremos el círculo unitario y lo graficaremos en el plano cartesiano.
Para ello, vamos a “desentrañar” el círculo unitario. Recordemos que para el círculo unitario las coordenadas son\((\cos \theta ,\sin \theta)\) donde θ es el ángulo central. Para graficar,\(y=\sin x\) reescribe las coordenadas como\((x,\sin x)\) donde\(x\) está el ángulo central, en radianes. Abajo expandimos las coordenadas sinusoidales para\(\dfrac{3\pi }{4}\).
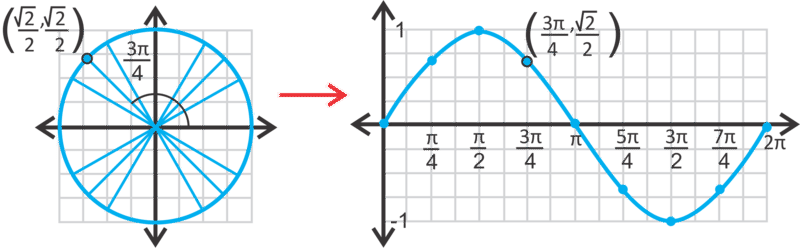
Observe que la curva varía de 1 a -1. El valor máximo es 1, que es at\(x=\dfrac{\pi }{2}\). El valor mínimo es -1 at\(x=\dfrac{3\pi }{2}\). Esta “altura” de la función sinusoidal se llama amplitud. La amplitud es el valor absoluto de promedio entre los puntos más altos y más bajos de la curva.
Ahora, mira el dominio. Parece que, si hubiéramos continuado la curva, se repetiría. Esto significa que la curva sinusoidal es periódica. Mira hacia atrás en el círculo unitario, el valor del seno cambia hasta que alcanza\(2\pi \). Después\(2\pi \), los valores sinusoidales se repiten. Por lo tanto, la curva anterior repetirá cada\(2\pi \) unidad, haciendo el periodo\(2\pi \). El dominio es todo números reales.

Del mismo modo, cuando expandimos la curva coseno\(y=\cos x\), desde el círculo unitario, tenemos:
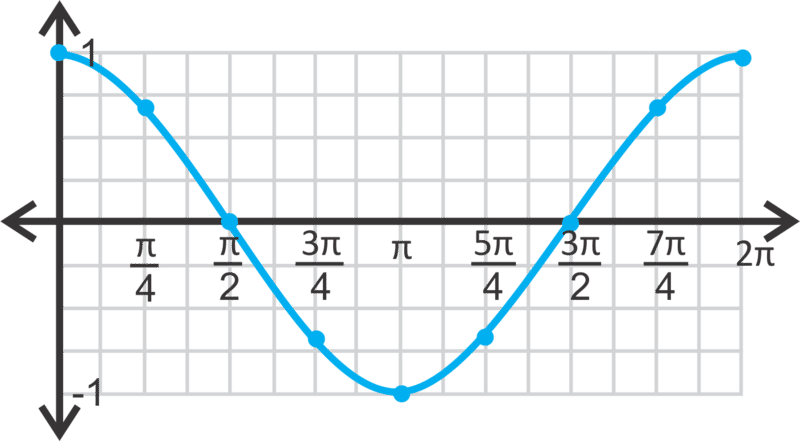
Observe que el rango también está entre 1 y -1 y el dominio serán todos números reales. La curva coseno también es periódica, con un periodo de\(2\pi \). Si dibujamos el gráfico pasado\(2\pi\), se vería así:

Comparando\(y=\sin x\) y\(y=\cos x\) (abajo), vemos que las curvas son casi idénticas, excepto que la curva sinusoidal comienza en\(y=0\) y la curva coseno comienza en\(y=1\).

Si desplazamos cualquiera de\(\dfrac{\pi }{2}\) las unidades de curva hacia la izquierda o hacia la derecha, se superpondrán. Cualquier desplazamiento horizontal de una función trigonométrica se denomina desplazamiento de fase.
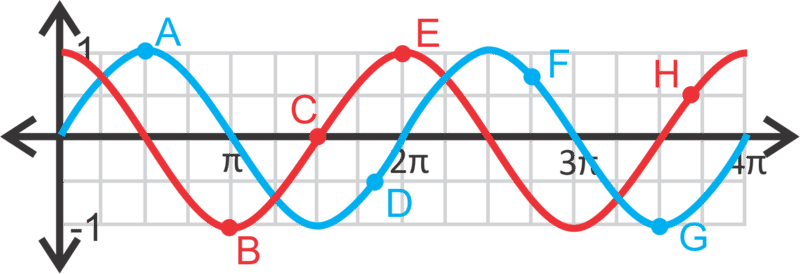
Identificemos los puntos resaltados en\(y=\sin x\) y\(y=\cos x\) a continuación.
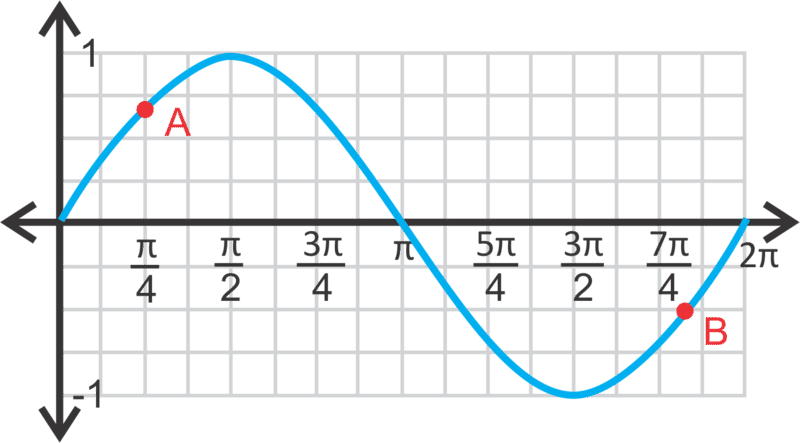
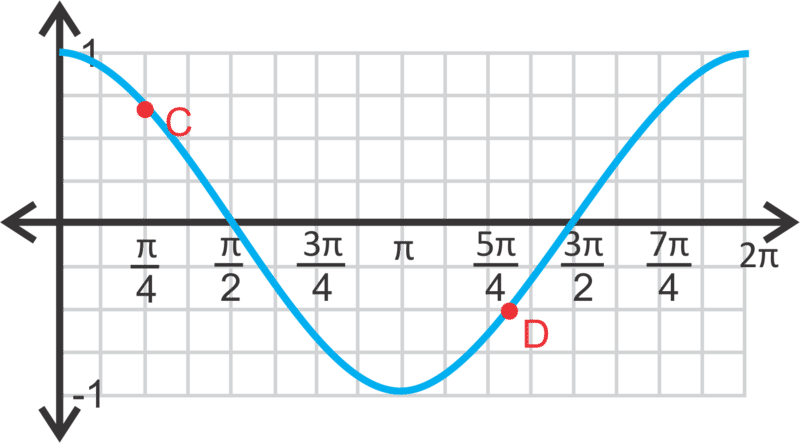
Para cada punto, piense en cuál es el valor de seno o coseno en esos valores. Para el punto A,\(\sin \dfrac{\pi }{4}=\dfrac{\sqrt{2}}{2}\), por lo tanto el punto es\(\left(\dfrac{\pi }{4},\dfrac{\sqrt{2}}{2}\right)\). Para el punto B, tenemos que trabajar hacia atrás porque no está exactamente en una línea vertical, sino en una horizontal. ¿Cuándo es\(\sin x=\dfrac{−1}{2}\)? Cuando\(x=\dfrac{7 \pi }{6}\) o\(\dfrac{11 \pi }{6}\). Al mirar la ubicación del punto B, sabemos que es la segunda opción. Por lo tanto, el punto es\(\left(\dfrac{11 \pi }{6}, \dfrac{1}{2}\right)\).
Para la curva coseno, el punto C es el mismo que el punto A porque el seno y el coseno para\(\dfrac{\pi }{4}\) es el mismo. En cuanto al punto D, utilizamos la misma lógica que hicimos para el punto B. ¿Cuándo lo hace\( \cos x=−\dfrac{1}{2}\)? Cuando\(x=\dfrac{2 \pi }{3}\) o\(\dfrac{4 \pi }{3}\). Nuevamente, mirando la ubicación del punto D, sabemos que es la segunda opción. El punto es\(\left(\dfrac{4\pi }{3}, \dfrac{1}{2}\right)\).
Amplitud
Además de graficar\(y=\sin x\) y\(y=\cos x\), podemos estirar las gráficas colocando un número frente al seno o coseno, como\(y=a\sin x\) o\(y=a\cos x\). \(\mid a \mid\)es la amplitud de la curva.
Vamos a graficar\(y=3\sin x\) a lo largo de dos periodos.
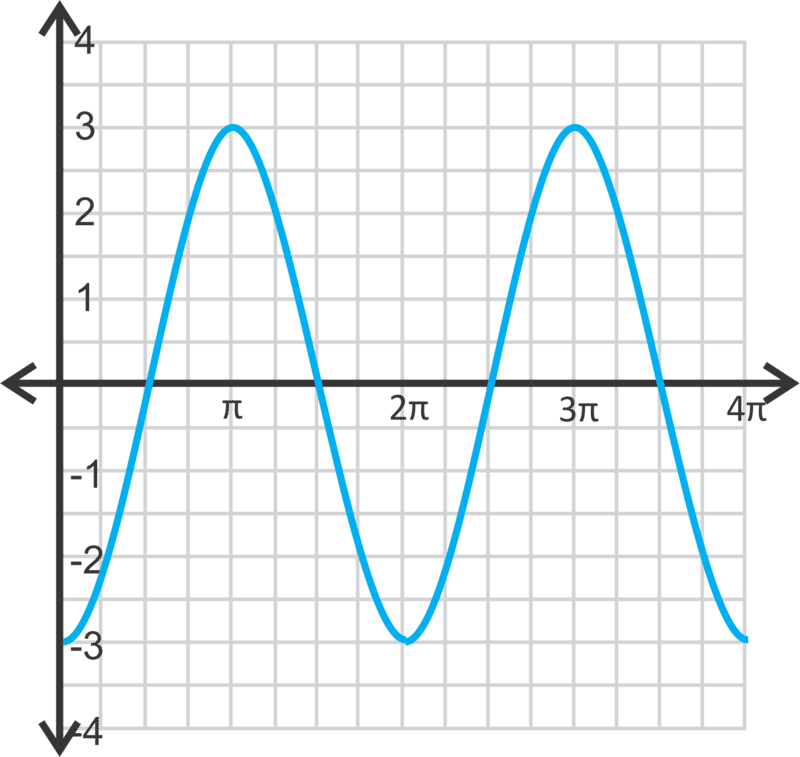
Comience con la curva sinusoidal básica. Recordemos que un periodo de la gráfica padre,\(y=\sin x\), es\(2\pi \). Por lo tanto, serán dos periodos\(4\pi \). El 3 indica que el rango ahora será de 3 a -3 y la curva se estirará para que el máximo sea 3 y el mínimo sea -3. La curva roja es\(y=3\sin x\).
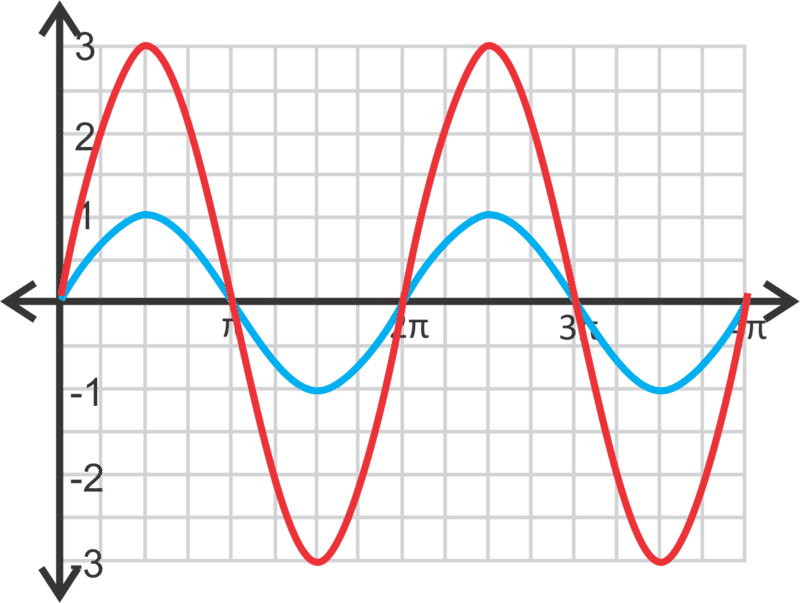
Observe que las intercepciones x son las mismas que la gráfica padre. Normalmente, cuando graficamos una función trigonométrica, siempre mostramos dos periodos completos de la función para indicar que sí se repite.
Ahora, vamos a graficar\(y=\dfrac{1}{2}\cos x\) a lo largo de dos periodos.
Ahora, la amplitud será 12 y la función será “suavizada” en lugar de estirada.
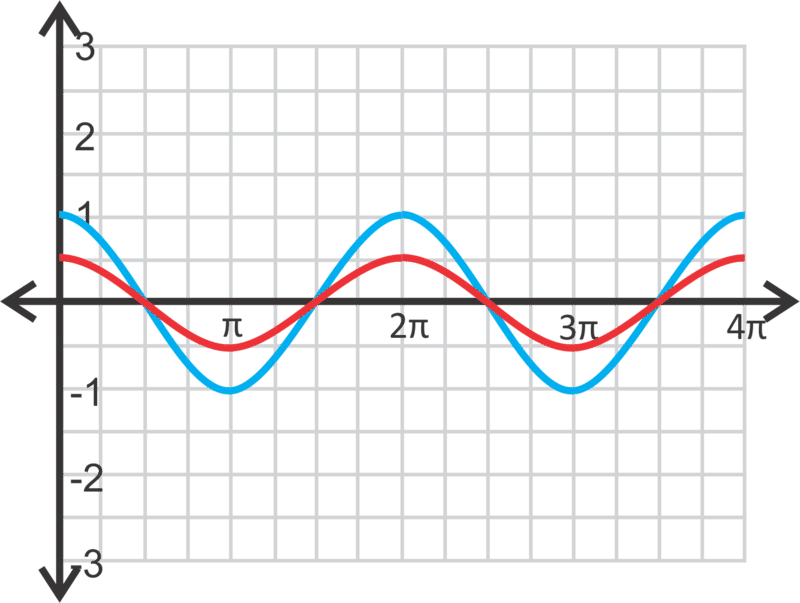
Por último, graficemos\(y=−\sin x\) a lo largo de dos periodos.
Los dos últimos problemas trataron de cambiar a y a fue positivo. Ahora, a es negativo. Al igual que con otras funciones, cuando el coeficiente inicial es negativo, la función se refleja sobre el eje x. \(y=−\sin x\)está en rojo.
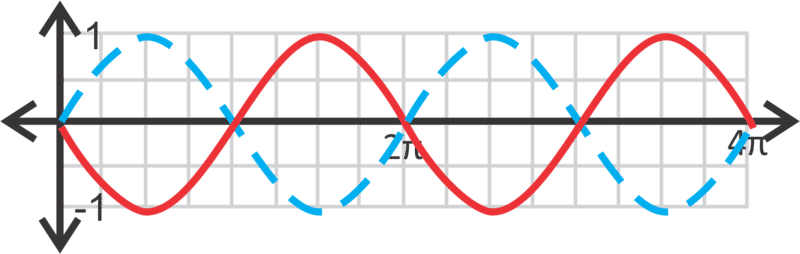
Anteriormente, se le pidió que encontrara el mínimo y el máximo de la gráfica\(y=2\cos x\).
Solución
El 2 frente a la función coseno indica que el rango ahora será de 2 a —2 y la curva se estirará de manera que el máximo sea 2 y el mínimo sea —2.
¿El punto está\(\left(\dfrac{5\pi }{6}, \dfrac{1}{2} \right)\) encendido\(y=\sin x\)? ¿Cómo lo sabes?
Solución
Sustituir en el punto por x e y y ver si la ecuación es verdadera.
\(\dfrac{1}{2}=\sin \left( \dfrac{5\pi }{6} \right)\)
Esto es cierto, así\(\left(\dfrac{5\pi }{6}, \dfrac{1}{2} \right)\) está en la gráfica.
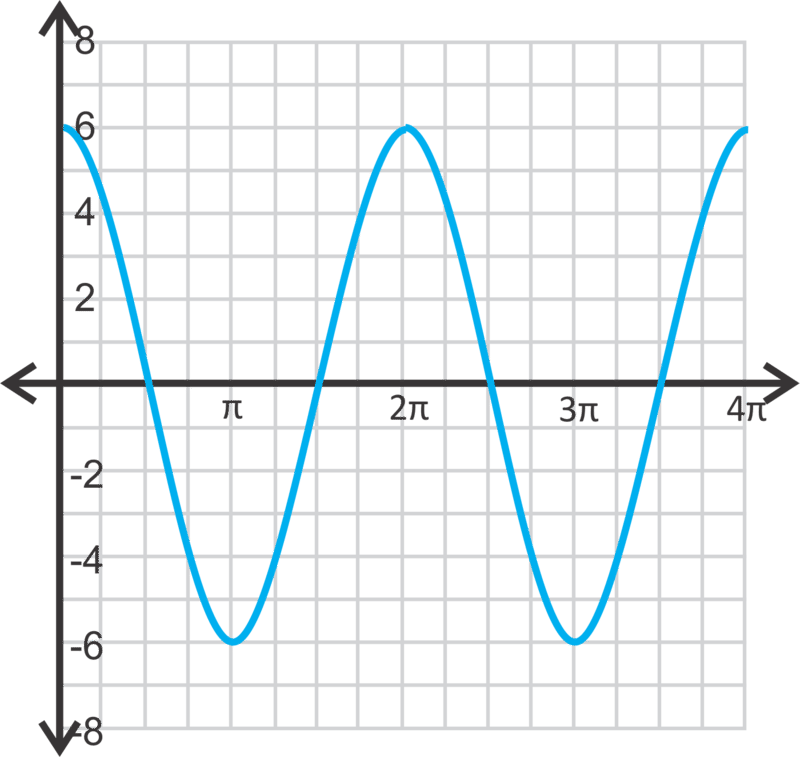
\(y=6\cos x\)
Solución
Estirar la curva coseno para que el máximo sea 6 y el mínimo sea -6.
\(y=−3\cos x\)
Solución
El gráfico se refleja sobre el eje x y se estira para que la amplitud sea 3.
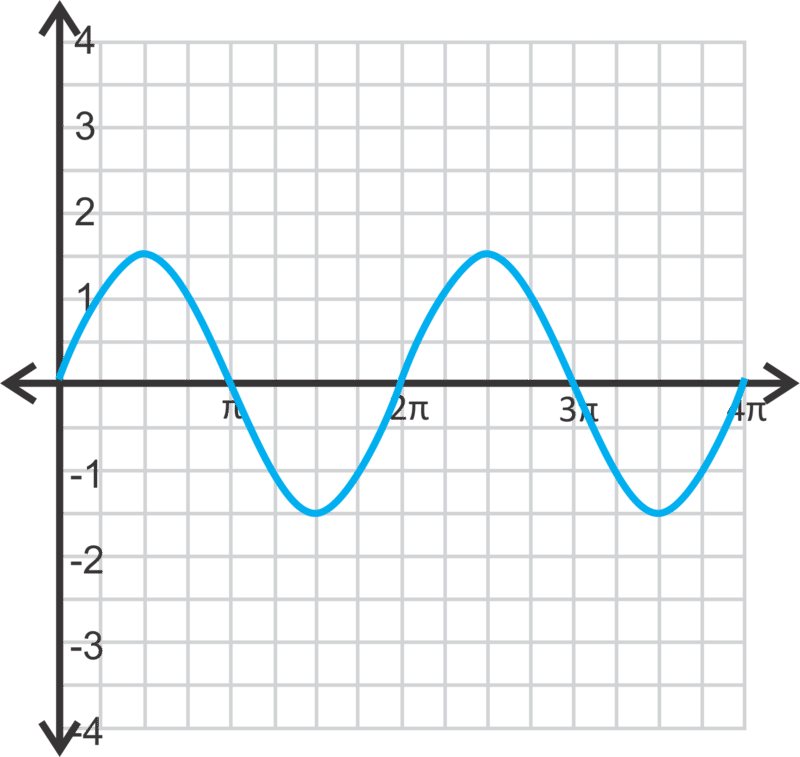
\(y=\dfrac{3}{2}\sin x\)
Solución
La fracción es equivalente a 1.5, haciendo 1.5 la amplitud.
Revisar
- Determinar el valor exacto de cada punto en\(y=\sin x\) o\(y=\cos x\).
Figura\(\PageIndex{14}\) - Enumere todos los puntos en el intervalo\([0, 4\pi ]\) donde\(\sin x=\cos x\). Usa la gráfica de #1 para ayudarte.
- Dibujar\(y=\sin x\) de\([0,2\pi ]\). Encontrar\(f\left(\dfrac{\pi }{3}\right)\) y\(f\left(\dfrac{5\pi }{3}\right)\). Trazar estos valores en la curva.
Para las preguntas 4-12, grafica la curva de seno o coseno en dos periodos.
- \(y=2\sin x\)
- \(y=−5\cos x\)
- \(y=\dfrac{1}{4}\cos x\)
- \(y=−\dfrac{2}{3}\sin x\)
- \(y=4\sin x\)
- \(y=−1.5\cos x\)
- \(y=\dfrac{5}{3}\cos x\)
- \(y=10\sin x\)
- \(y=−7.2\sin x\)
- Gráfica\(y=\sin x\) y\(y=\cos x\) en el mismo conjunto de ejes. ¿Cuántas unidades tendrías que desplazar la curva sinusoidal (hacia la izquierda o hacia la derecha) para que se superponga perfectamente a la curva coseno?
- Gráfica\(y=\sin x\) y\(y=−\cos x\) en el mismo conjunto de ejes. ¿Cuántas unidades tendrías que desplazar la curva sinusoidal (hacia la izquierda o derecha) para que se superponga perfectamente\(y=−\cos x\)?
Escribe la ecuación para cada curva de seno o coseno a continuación. \(a>0\)para ambas preguntas.
-
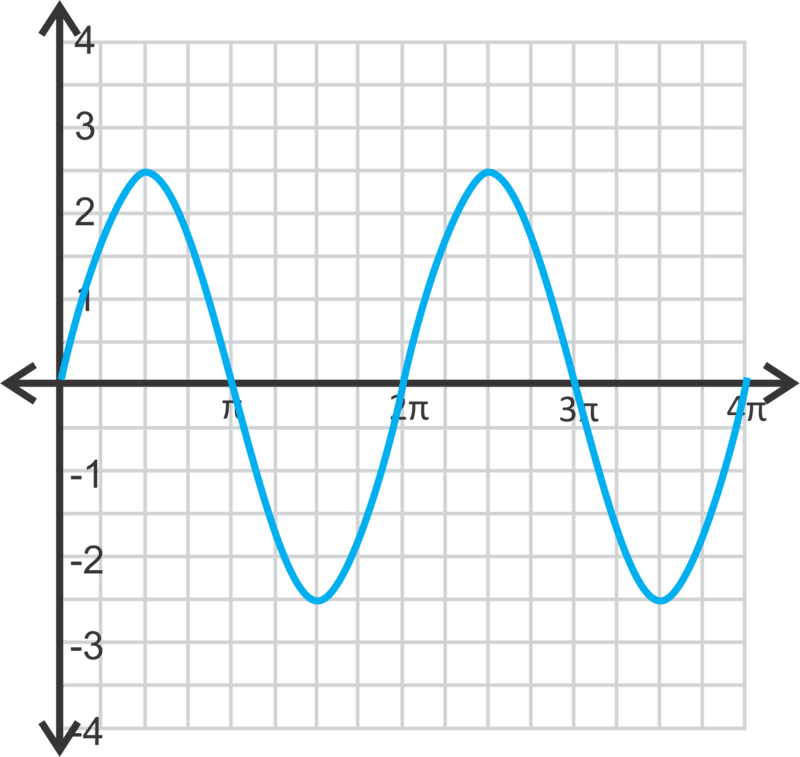
Figura\(\PageIndex{15}\) -
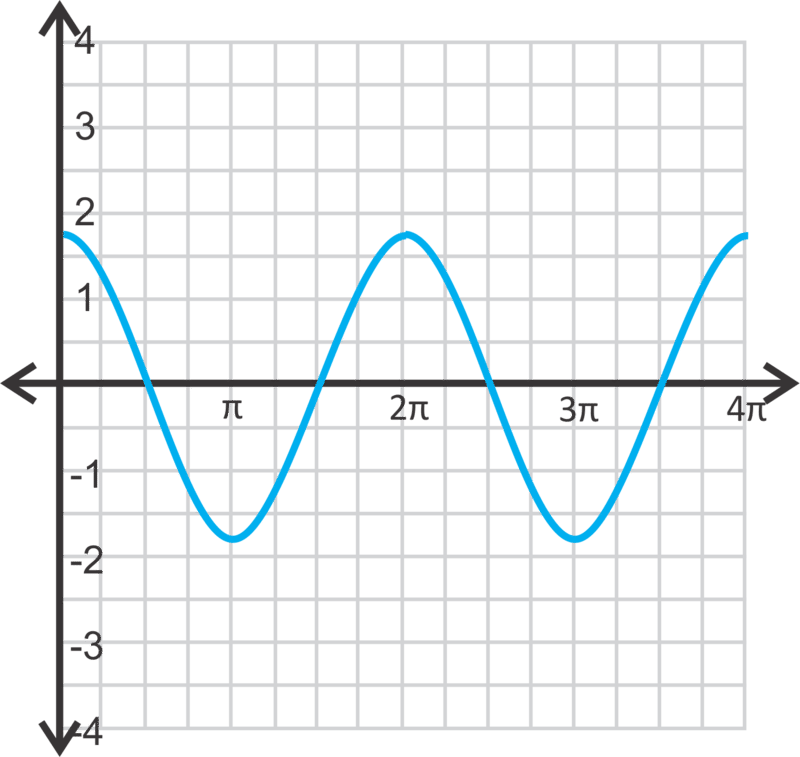
Figura\(\PageIndex{16}\)
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 14.1.
Recursos adicionales
Video: Gráficas de funciones de seno y coseno - Descripción general
Práctica: Gráfica sinusoidal y gráfica de coseno

