2.7.3: Gráficas tangentes y cotangentes

Involucrar asíntotas separadas por\(\pi\) radianes.

¿Y si tu instructor te diera un conjunto de gráficas como estas?

Figura\(\PageIndex{1}\)

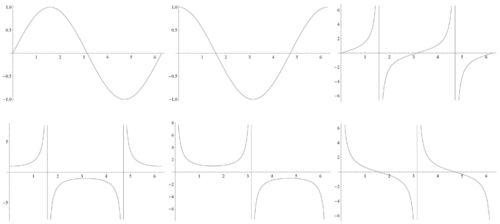
y le pidió que identificara cuáles eran las gráficas de las funciones tangente y cotangente?

Gráficas tangentes y cotangentes

El nombre de la función tangente proviene de la línea tangente de un círculo. Esta es una línea que es perpendicular al radio en un punto del círculo para que la línea toque el círculo exactamente en un punto.

Figura\(\PageIndex{2}\)

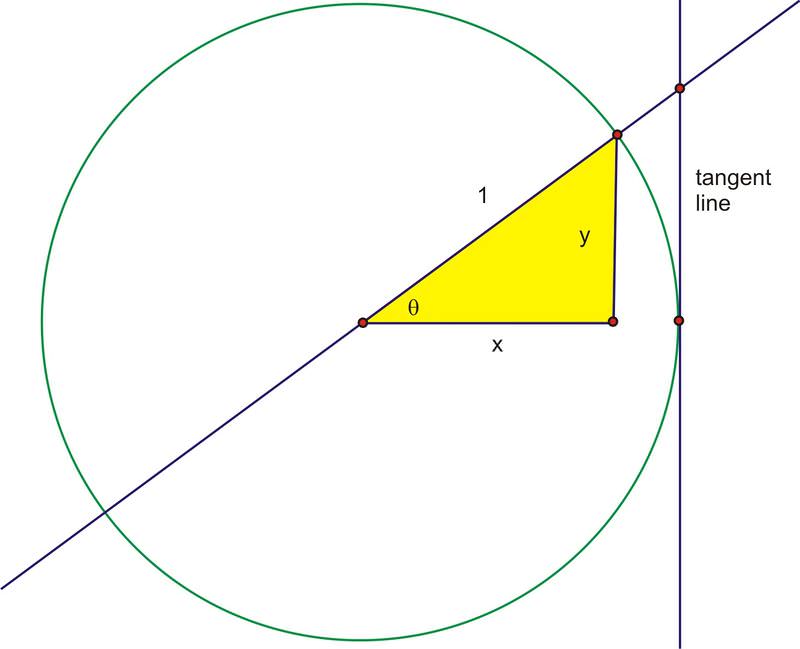
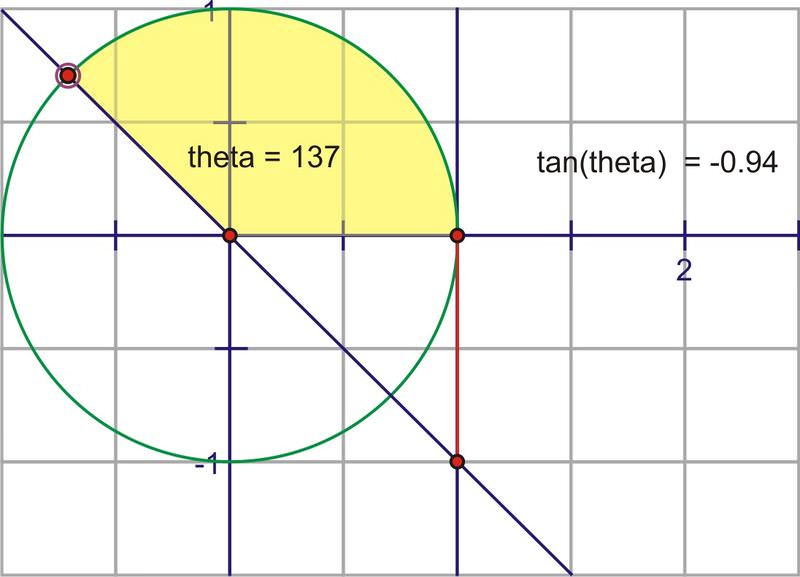
Si extendemos ángulo\(\theta \) a través del círculo unitario para que se cruce con la línea tangente,\(\tan \theta \) será igual a la longitud del segmento rojo. A continuación, este segmento se etiqueta como el “segmento tangente”.

Figura\(\PageIndex{3}\)

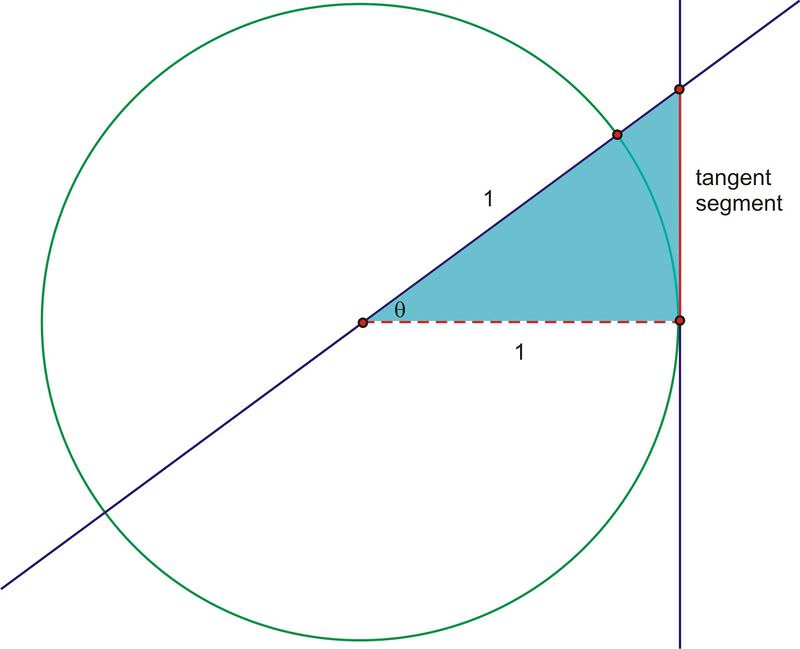
¿Por qué? El segmento discontinuas es 1 porque es el radio del círculo unitario. Recordemos que en general,\(\tan \theta =\dfrac{y}{x}\). Así que aquí,\(\tan \theta =\dfrac{\text{tangent segment}}{1}=\text{tangent segment}\)

A medida que\(\theta \) aumenta el valor de, el valor de\(\tan \theta\) los cambios. A medida que rotemos por el primer cuadrante, el valor de\(\tan \theta \) aumentará muy lentamente al principio y luego más rápidamente.

Figura\(\PageIndex{4}\)

Figura\(\PageIndex{5}\)

Figura\(\PageIndex{6}\)

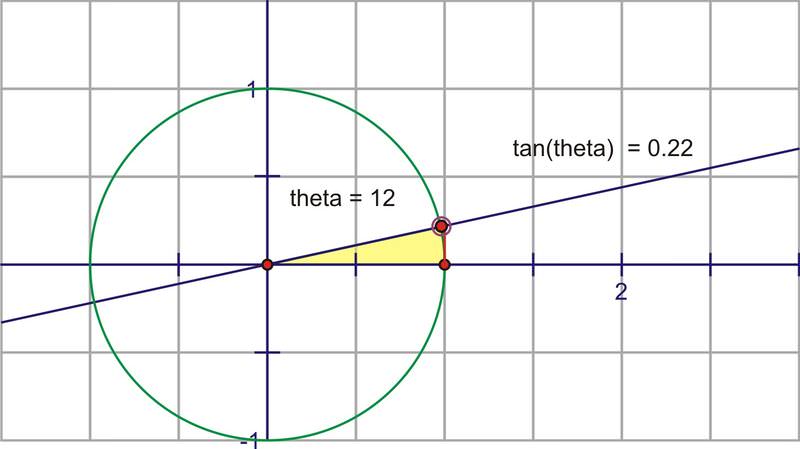
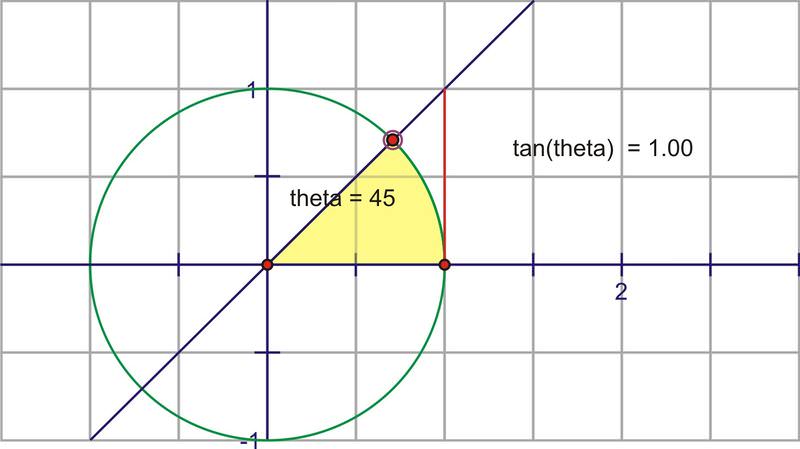
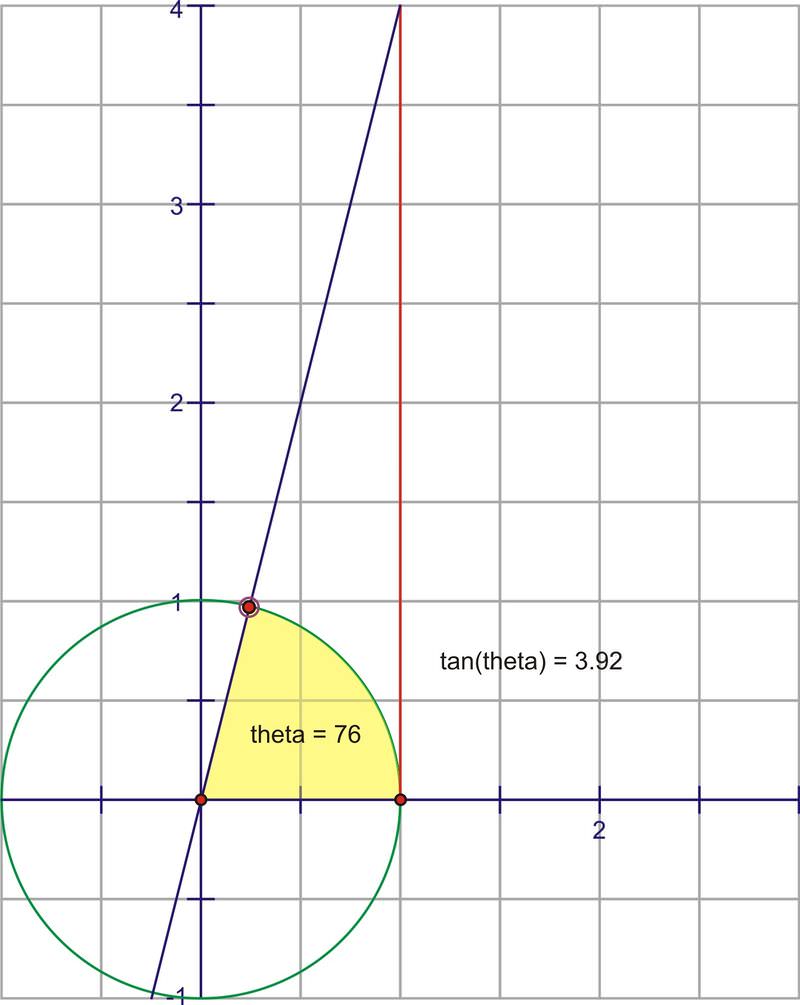
A medida que nos acercamos mucho al eje y el segmento se vuelve infinitamente grande, hasta que el ángulo realmente golpea\( 90^{\circ}\), momento en el que la extensión del ángulo y la línea tangente serán realmente paralelas y por lo tanto nunca se cruzarán.

Figura\(\PageIndex{7}\)

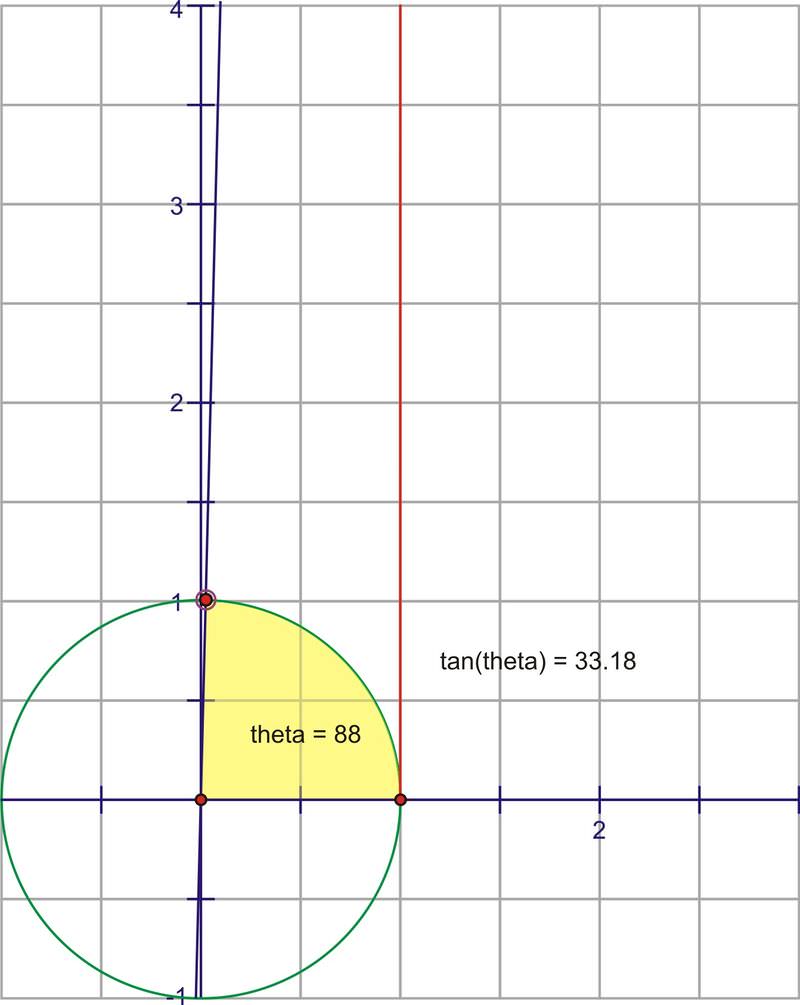
Esto significa que no hay una longitud finita del segmento tangente, o el segmento tangente es infinitamente grande.

Traduzcamos esta parte de la gráfica al plano de coordenadas. Trazar\((\theta ,\tan \theta )\) como\((x,y)\).

Figura\(\PageIndex{8}\)

Figura\(\PageIndex{9}\)

Figura\(\PageIndex{10}\)

Figura\(\PageIndex{11}\)

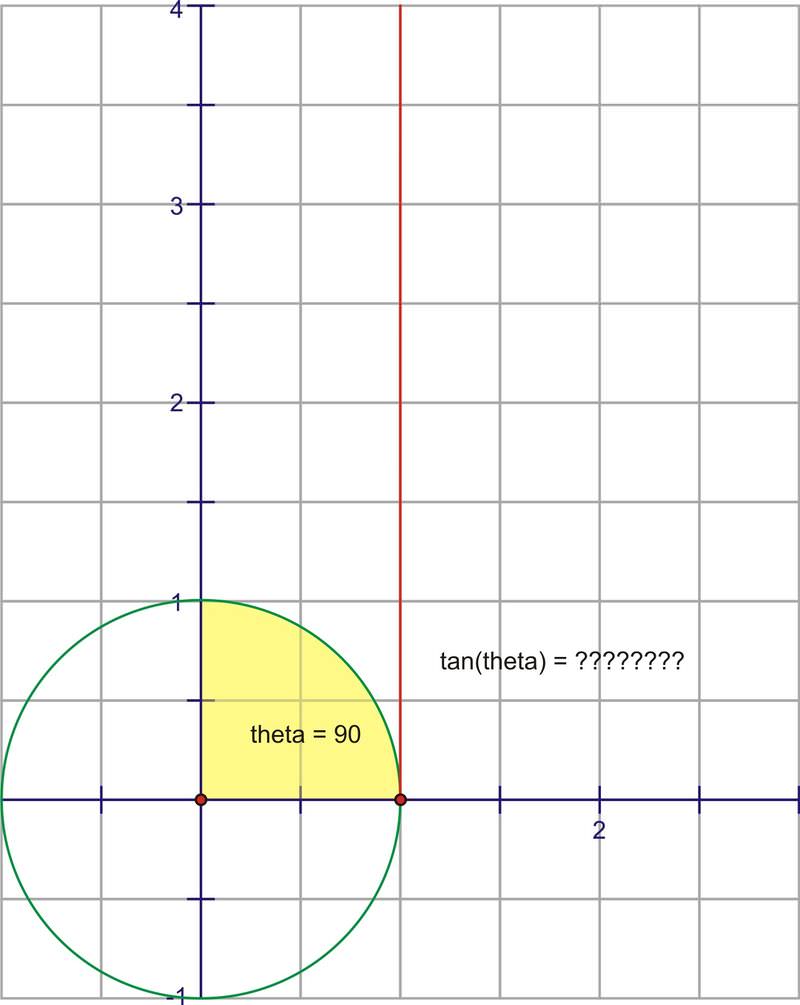
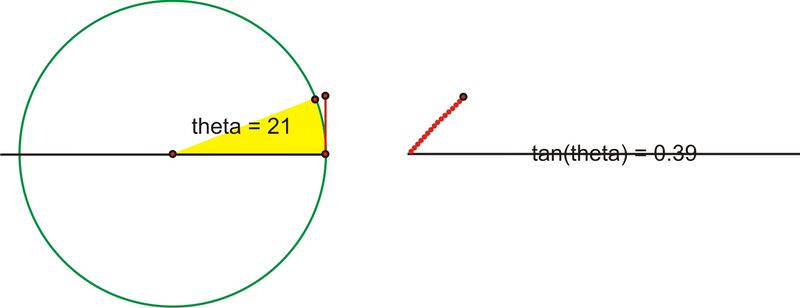
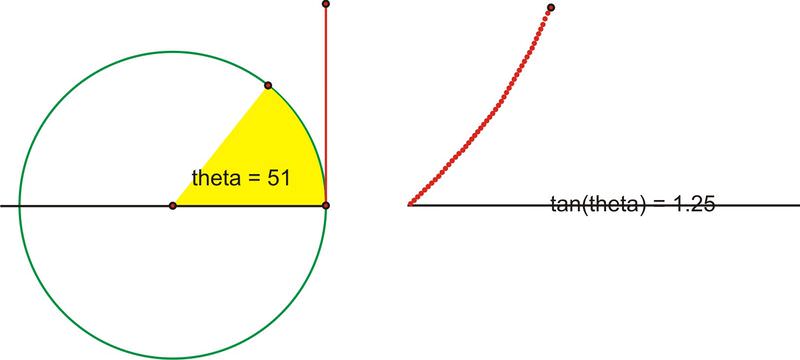
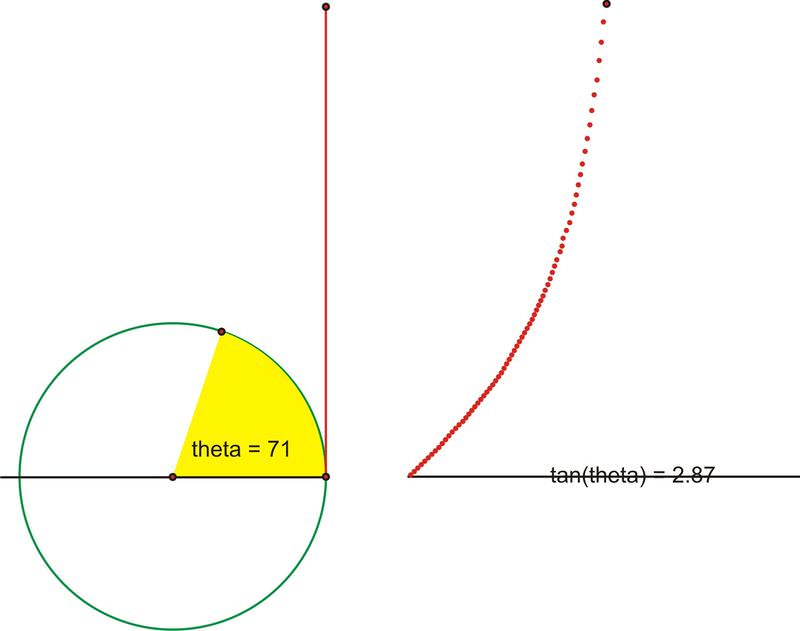
De hecho\(90^{\circ}\), a medida que nos acercamos infinitamente, el valor de la tangente aumenta sin límite, hasta cuando realmente alcanzamos\(90^{\circ}\), momento en el que la tangente es indefinida. Recordemos que hay algunos ángulos (\(90^{\circ}\)y\(270^{\circ}\), por ejemplo) para los cuales no se define la tangente. Por lo tanto, en estos puntos, van a haber asíntotas verticales.

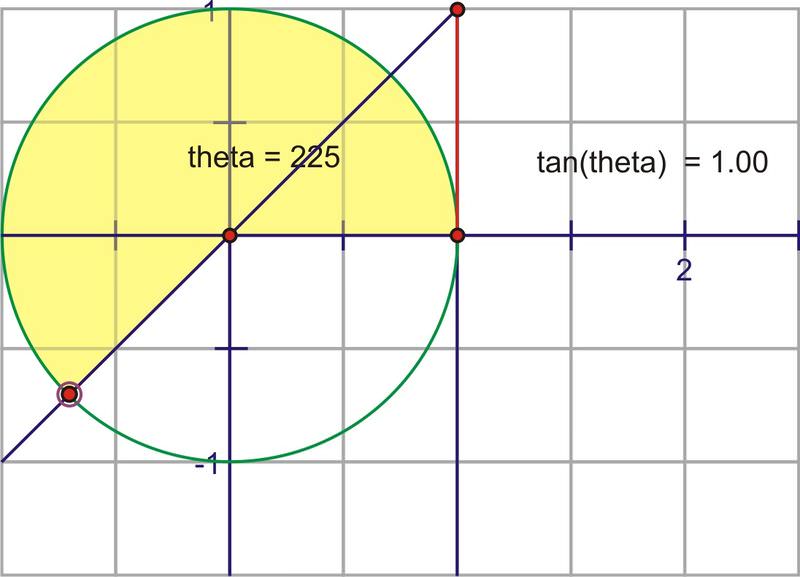
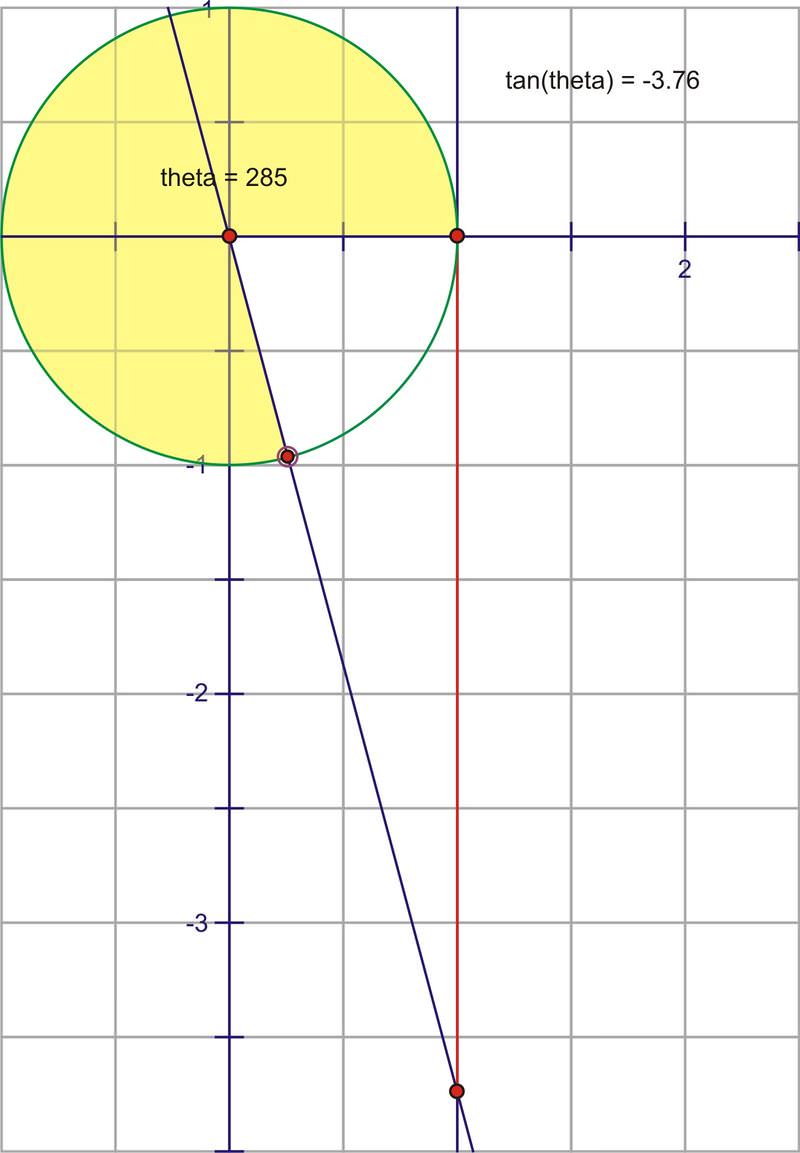
Girando más allá\(90^{\circ}\), la intersección de la extensión del ángulo y la línea tangente está realmente por debajo del eje x. Esto encaja muy bien con lo que sabemos de que la tangente para un ángulo de\(2^{nd}\) cuadrante es negativa. Al principio, tendrá valores negativos muy grandes, pero a medida que el ángulo gira, el segmento se acorta, llega a 0, luego vuelve a cruzar hacia los números positivos a medida que el ángulo entra en el\(3^{rd}\) cuadrante. El segmento volverá a ser infinitamente grande a medida que se acerque\(270^{\circ}\). Después de ser indefinido en\(270^{\circ}\), el ángulo cruza hacia el\(4^{th}\) cuadrante y una vez más cambia de ser infinitamente negativo, a acercarse a cero a medida que completamos una rotación completa.

Figura\(\PageIndex{12}\)

Figura\(\PageIndex{13}\)

Figura\(\PageIndex{14}\)

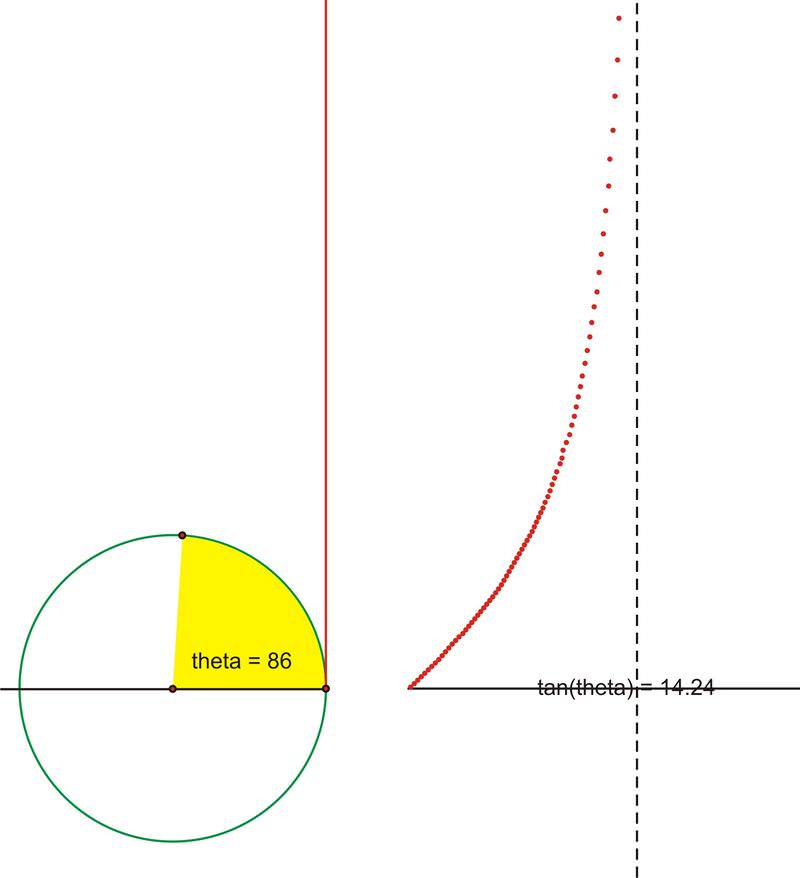
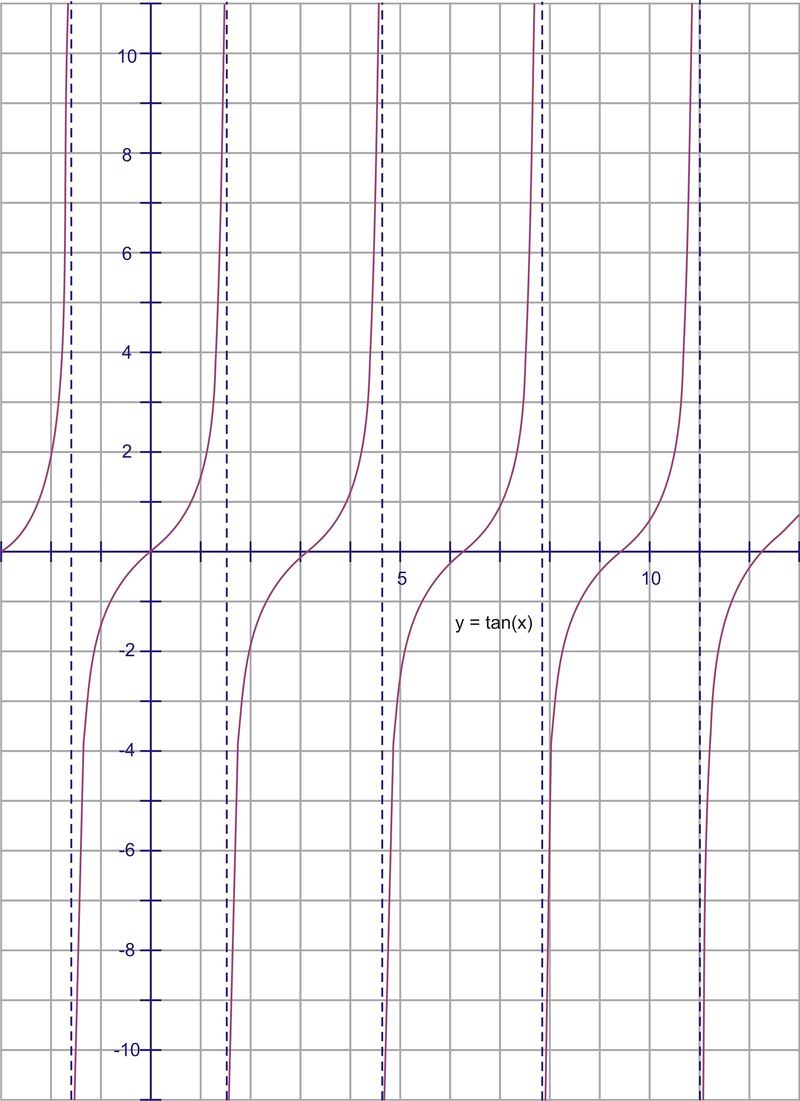
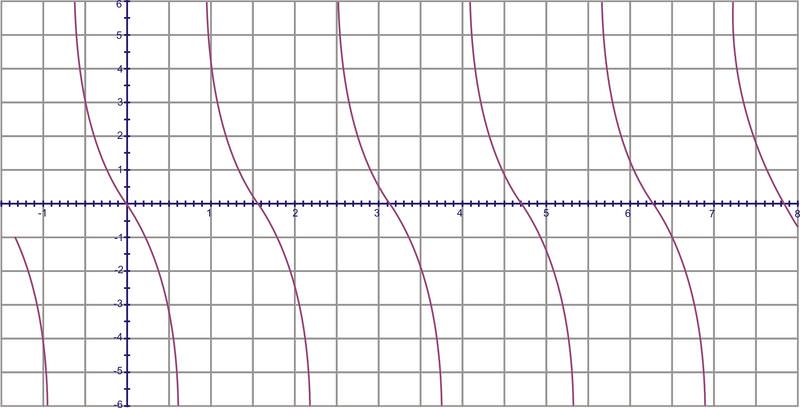
La gráfica\(y=\tan x\) sobre varias rotaciones se vería así:

Figura\(\PageIndex{15}\)

Observe que el eje x se mide en radianes. Nuestras asíntotas ocurren cada\(\pi \) radianes, comenzando en\(\dfrac{\pi}{2}\). El periodo de la gráfica es, por lo tanto,\(\pi \) radianes. El dominio es todo real excepto las asíntotas en\(\dfrac{\pi}{2},\; \dfrac{3\pi}{2} ,\; −\dfrac{\pi}{2}\), etc. y el rango es todo números reales.

cotangente es el recíproco de tangente\(\dfrac{x}{y}\), por lo que tendría sentido que donde alguna vez la tangente tuviera una asíntota, ahora la cotangente será cero. Lo contrario de esto también es cierto. Cuando la tangente es cero, ahora la cotangente tendrá una asíntota. La forma de la curva es generalmente la misma, por lo que la gráfica se ve así:

Figura\(\PageIndex{16}\)

Figura\(\PageIndex{17}\)

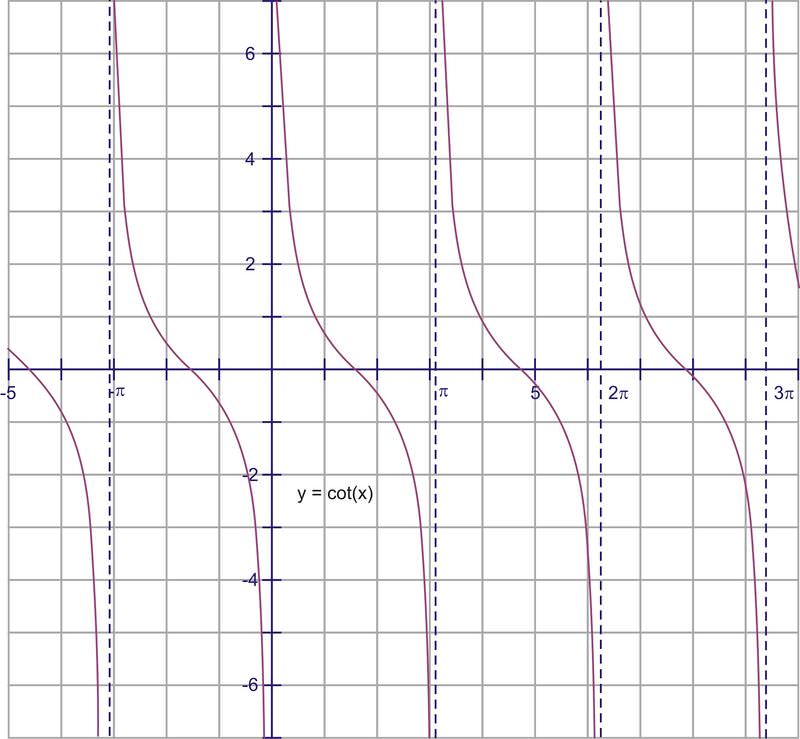
Cuando superponga las dos funciones, observe que las gráficas se cruzan consistentemente en 1 y -1. Estos son los ángulos que tienen\(45^{\circ}\) como ángulos de referencia, que siempre tienen tangentes y cotangentes iguales a 1 o -1. Tiene sentido que 1 y -1 sean los únicos valores para los que una función y su recíproco son iguales. Tenga esto en cuenta mientras miramos cosecante y secante en comparación con sus recíprocos de seno y coseno.

La función cotangente tiene un dominio de todos los ángulos reales excepto múltiplos de\(\pi {\ldots −2\pi ,−\pi , 0, \pi , 2\pi \ldots}\) El rango es todos números reales.

Croquizar gráficos

1. Esbozar el gráfico de\(g(x)=−2+\cot \dfrac{1}{3}x\) sobre el intervalo\([0,6\pi ]\)

A partir de\(y=\cot x\), se\(g(x)\) desplazaría hacia abajo dos y la frecuencia es\(\dfrac{1}{3}\), lo que significa que el periodo sería\(3\pi \), en lugar de\(9\pi \). Entonces, en nuestro intervalo de\([0,6\pi ]\) habría dos repeticiones completas. El gráfico rojo es\(y=\cot x\).

Figura\(\PageIndex{18}\)

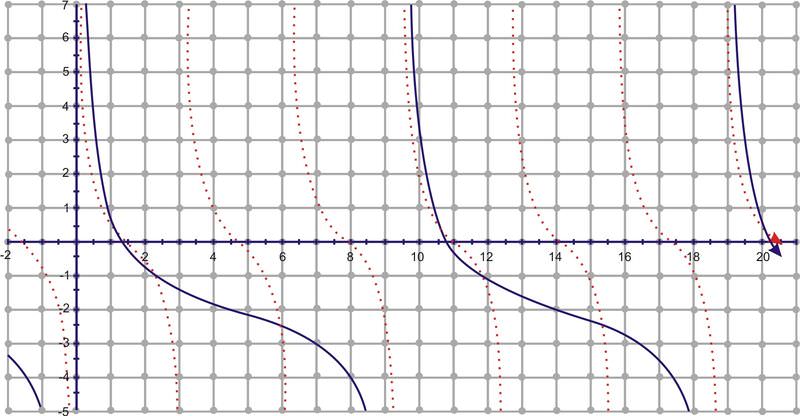
2. Esbozar el gráfico de\(y=−3\tan \left(x−\dfrac{\pi}{4} \right)\) sobre el intervalo\([−\pi , 2\pi ]\)

Si comparas esta gráfica con\(y=\tan x\), se estirará y volteará. También tendrá un desplazamiento de fase de\(\dfrac{\pi}{4} \) a la derecha. El gráfico rojo es\(y=\tan x\).

Figura\(\PageIndex{19}\)

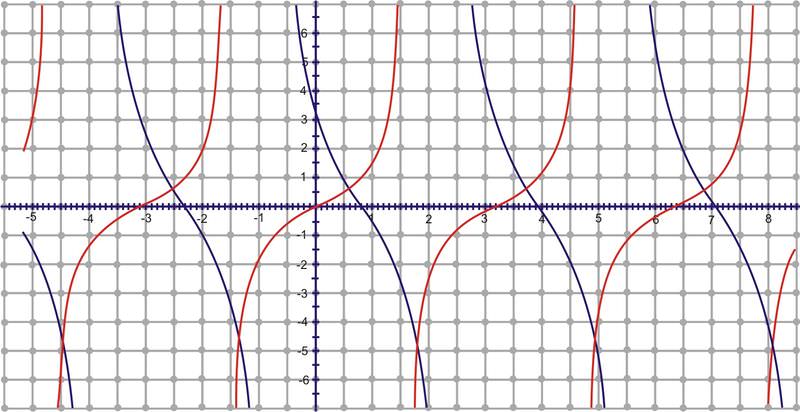
3. Esbozar el gráfico de\(h(x)=4\tan \left(x+\dfrac{\pi}{2}\right)+3\) sobre el intervalo\([0,2\pi ]\)

La constante frente a la función tangente provocará que la gráfica se estire. También tendrá un desplazamiento de fase de\(\dfrac{\pi}{2}\) a la izquierda. Por último, la gráfica se desplazará tres hacia arriba. Aquí puedes ver ambas gráficas, donde está la gráfica roja\(y=\tan x\).

Figura\(\PageIndex{20}\)

Ejemplo\(\PageIndex{1}\)

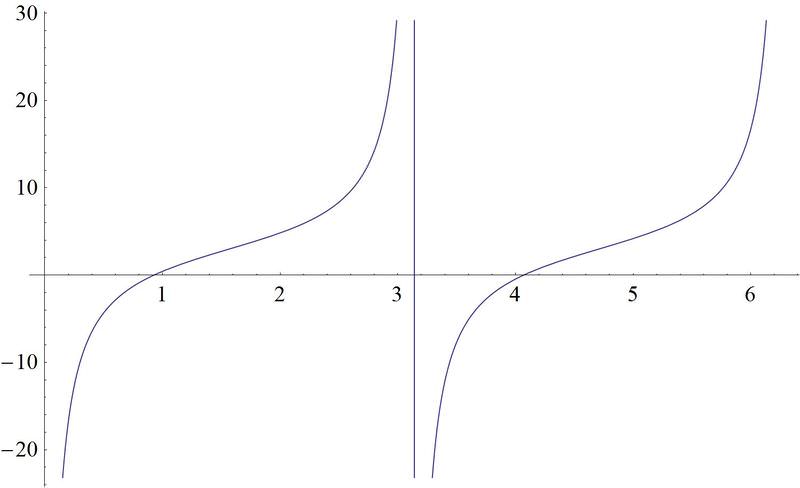
Anteriormente, se le pidió que identificara qué gráficas son tangentes y cotangentes.

Solución

Como se puede observar después de completar esta sección, cuando se le presentan las gráficas:

1. 

   Figura\(\PageIndex{21}\)

2. 

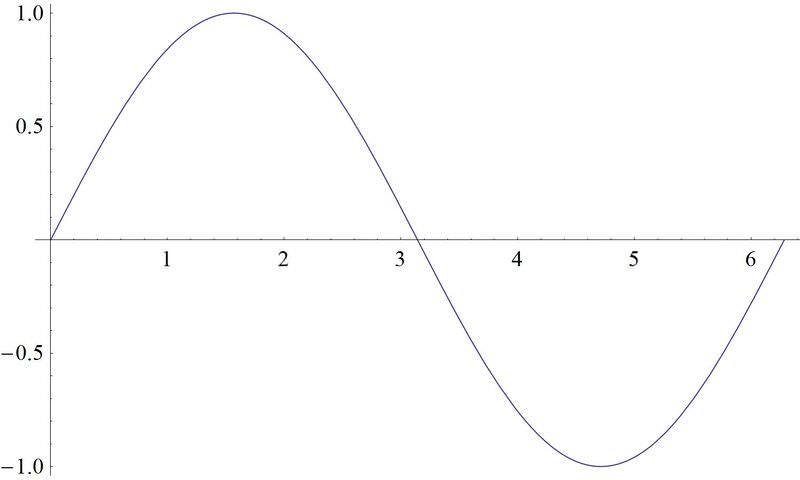
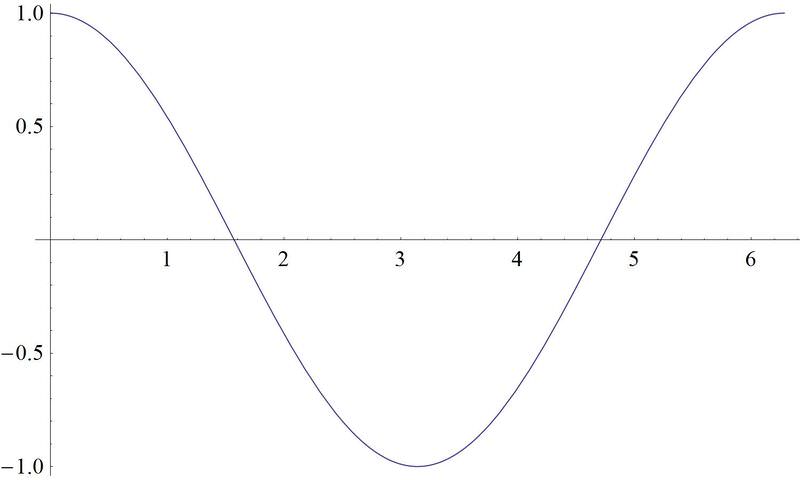
   Figura\(\PageIndex{22}\)

3. 

   Figura\(\PageIndex{23}\)

4. 

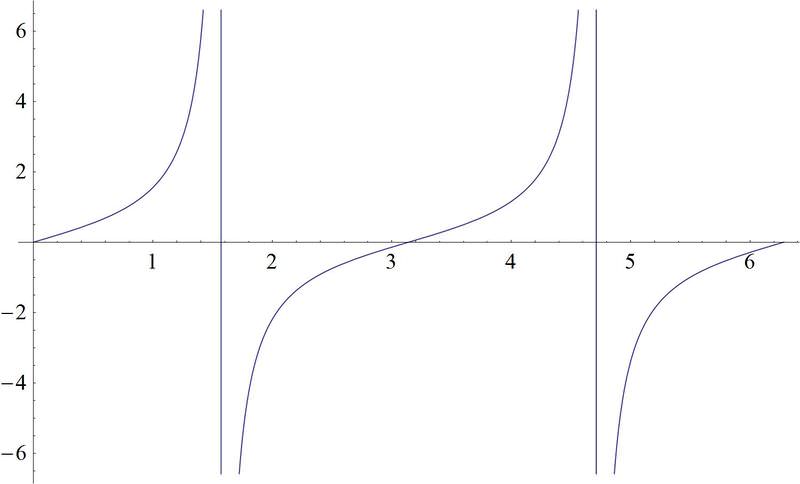
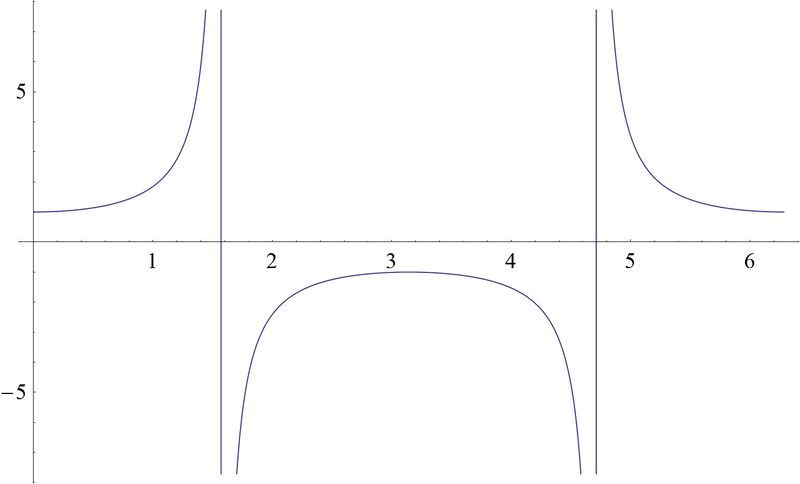
   Figura\(\PageIndex{24}\)

5. 

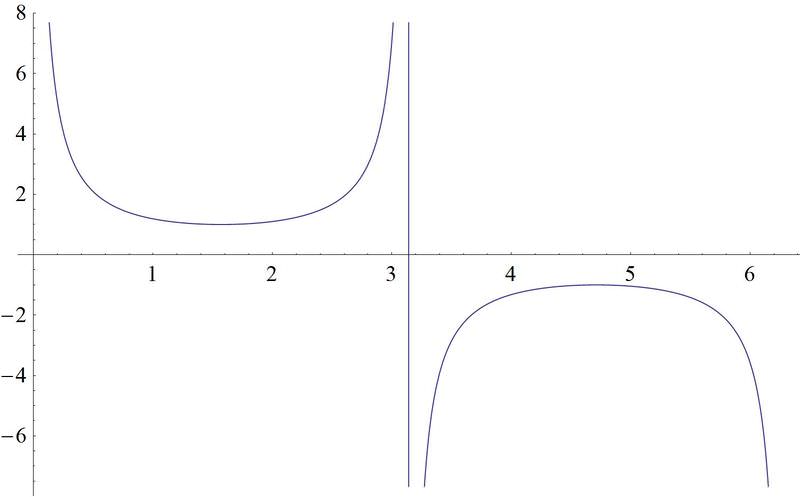
   Figura\(\PageIndex{25}\)

6. 

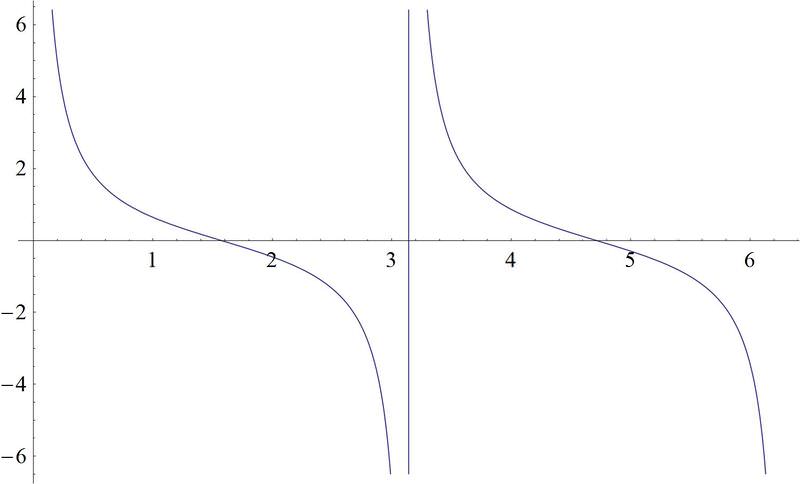
   Figura\(\PageIndex{26}\)

Las gráficas tangente y cotangente son las gráficas tercera y sexta.

Ejemplo\(\PageIndex{2}\)

Gráfica\(y=−1+\dfrac{1}{3}\cot 2x\)

Solución

Figura\(\PageIndex{27}\)

Ejemplo\(\PageIndex{4}\)

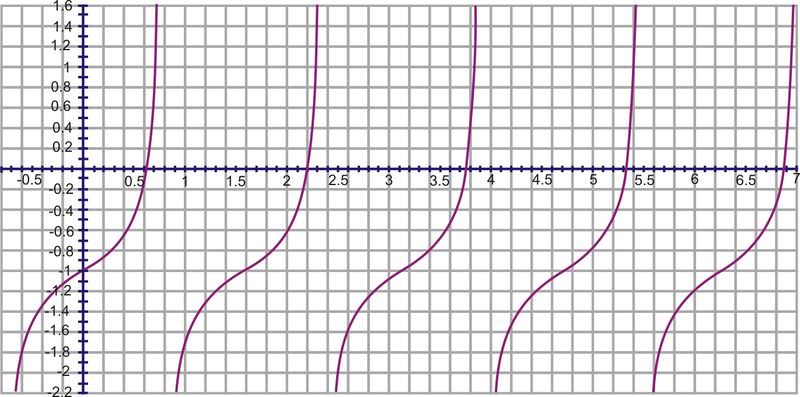
Gráfica\(f(x)=4+\tan (0.5(x−\pi ))\)

Solución

Figura\(\PageIndex{28}\)

Ejemplo\(\PageIndex{5}\)

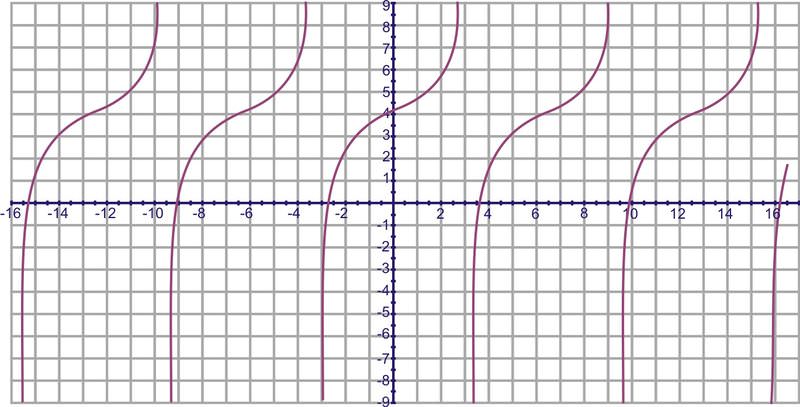
Gráfica\(y=−2\tan 2x\)

Solución

Figura\(\PageIndex{29}\)

Revisar

Grafica cada una de las siguientes funciones

1. \(f(x)=\tan (x)\)
2. \(h(x)=\tan (2x)\)
3. \(k(x)=\tan (2x+\pi )\)
4. \(m(x)=−\tan (2x+\pi )\)
5. \(g(x)=−\tan (2x+\pi )+3\)
6. \(f(x)=\cot (x)\)
7. \(h(x)=\cot (2x)\)
8. \(k(x)=\cot (2x+\pi )\)
9. \(m(x)=3\cot (2x+\pi )\)
10. \(g(x)=−2+3\cot (2x+\pi )\)
11. \(h(x)=\tan \left(\dfrac{x}{2}\right)\)
12. \(k(x)=\tan \left(\dfrac{x}{2}+\dfrac{\pi}{4} \right)\)
13. \(m(x)=3\tan \left(\dfrac{x}{2}+\dfrac{\pi}{4} \right)\)
14. \(g(x)=3\tan \left(\dfrac{x}{2}+\dfrac{\pi}{4} \right)−1\)
15. \(h(x)=\cot \left(\dfrac{x}{2}\right)\)
16. \(k(x)=\cot \left(\dfrac{x}{2}+\dfrac{3\pi}{2} \right)\)
17. \(m(x)=−3\cot \left(\dfrac{x}{2}+\dfrac{3\pi}{2} \right)\)
18. \(g(x)=2−3\cot \left(\dfrac{x}{2}+\dfrac{3\pi}{2} \right)\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.11.

El vocabulario

Término	Definición
Función Circular	Una función circular es una función medida al examinar el ángulo de rotación alrededor del plano de coordenadas.

Recursos adicionales

Video: Animación: Graficando la Función Tangente Usando el Círculo de Unidad

Práctica: Gráficas tangentes y cotangentes