3.2.8: Ecuaciones Trigonométricas Usando Factorización

Factoraje y la Fórmula Cuadrática.

Resolver ecuaciones trigonométricas es un proceso importante en matemáticas. Muy a menudo verás potencias de funciones trigonométricas y se te pedirá que resuelvas los valores de la variable que hacen verdadera la ecuación. Por ejemplo, supongamos que se le dio la ecuación trigonométrica

\(2\sin x \cos x=\cos x\)

Ecuaciones trigonométricas mediante factorización

Sin duda ha tenido experiencia con el factoring. Probablemente hayas factorizado ecuaciones a la hora de buscar los posibles valores de alguna variable, como "\(x\)”. Podría interesarle descubrir que puede usar el mismo método de factorización para algo más que una variable que es un número. Se pueden factorizar ecuaciones trigonométricas para encontrar los posibles valores que la función puede tomar para satisfacer una ecuación.

Las habilidades algebraicas como factorización y sustitución que se utilizan para resolver diversas ecuaciones son muy útiles a la hora de resolver ecuaciones trigonométricas. Al igual que con las expresiones algebraicas, hay que tener cuidado para evitar dividir por cero durante estas maniobras.

Resolviendo valores desconocidos

1. Resolver\(2\sin^2 x−3\sin x+1=0\) para\(0<x \leq 2\pi\).

\(\begin{aligned} \qquad \qquad \quad x^2 \sin^2 x−3\sin x+1&=0 \qquad \text{Factor this like a quadratic equation} \\ \qquad \qquad \quad (2\sin x−1)(\sin x−1)&=0 \end{aligned} \\ \begin{aligned} & \downarrow & \searrow& \\ 2\sin x−1&=0 &\text{or} \quad \sin x−1&=0 \\ 2\sin x&=1 & \sin x&=1 \\ \sin x&=\dfrac{1}{2} & x&=\dfrac{\pi}{2} \\ x=\dfrac{\pi}{6} \text{ and } x&=\dfrac{5\pi}{6} & & \end{aligned} \)

2. Resolver\(2 \tan x \sin x+2\sin x=\tan x+1\) para todos los valores de\(x\).

Figura\(\PageIndex{1}\)

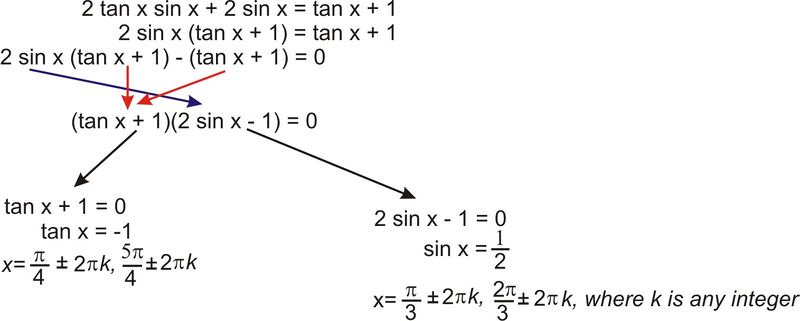
Saque\(\sin x\)

Hay un factor común de\((\tan x+1)\)

\(−(\tan x+1)\)Piense en el as\((−1)(\tan x+1)\), razón por la cual hay un\(−1\) detrás del\(2 \sin x\).

3. Resolver\(2\sin^2 x+3\sin x−2=0\) para todos\(x\),\([0,\pi ]\).

\ (\ begin {alineado}
\ qquad\ quad 2\ sin ^ {2} x+3\ sin x-2&=0\ fila derecha\ texto {Factor como cuadrático}\\
\ qquad\ quad (2\ sin x-1) (\ sin x+2) &=0\ end {alineado}\\\ begin {alineado}\\ swarrow&&\ qquad\ searrow &\
2\ sin x-1 &=0 &\ sin x+2& ; =0\\
\ sin x&=\ dfrac {1} {2} &\ sin x&=-2\ final {alineado}\)
\(x=\dfrac{\pi}{6} \text { and } x=\dfrac{5 \pi}{6} \text { There is no solution because the range of } \sin x \text { is }[-1,1] \text { . }\)

Algunas ecuaciones trigonométricas no tienen soluciones. Esto significa que no hay reemplazo para la variable que dará como resultado una expresión verdadera.

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le pidió que resolviera esto:

\(2 \sin x \cos x=\cos x\)

Solución

Restar\(\cos x\) de ambos lados y factorizarla fuera de la ecuación:

\(\begin{aligned} 2\sin x \cos x−\cos x&=0 \\ \cos x(2\sin x−1)&=0 \end{aligned}\)

Ahora establece cada factor igual a cero y resuelve. El primero es\(\cos x\):

\(\begin{aligned} \cos x&=0 \\ x&=\dfrac{\pi}{2},\; \dfrac{3\pi }{2}\end{aligned}\)

Y ahora para el otro término:

\(\begin{aligned} 2 \sin x−1&=0 \\ \sin x&=\dfrac{1}{2} \\ x&=\dfrac{\pi}{6},\; \dfrac{5\pi}{6}\end{aligned}\)

Ejemplo\(\PageIndex{2}\)

Resolver la ecuación trigonométrica de\(4 \sin x \cos x+2\cos x−2\sin x−1=0\) tal manera que\(0\leq x<2\pi\).

Solución

Utilice factorización por agrupación.

Figura\(\PageIndex{2}\)

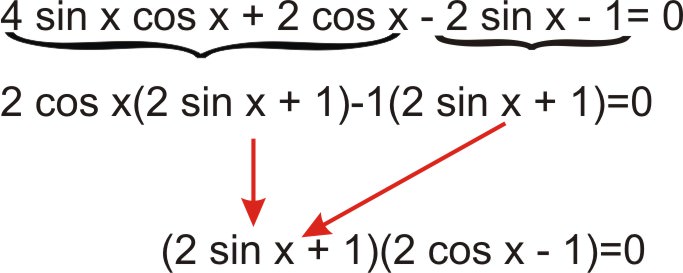
\ (\ begin {alineado}
2\ sin x+1&=0 &\ text {o}\ qquad 2\ cos x-1&=0\\
2\ sin x&=-1 & 2\ cos x&=1\
\ sin x&=-\ dfrac {1} {2} &\ cos x&=\ dfrac {1} {2}\
x&=\ dfrac {7\ pi} {6},\;\ dfrac {11\ pi} {6} & x&=\ dfrac { \ pi} {3},\;\ dfrac {5\ pi} {3}
\ final {alineado}\)

Ejemplo\(\PageIndex{3}\)

Resolver\(\tan^2 x=3\tan x\) por\(x\) más\([0,\pi ]\).

Solución

\ (\ begin {alineado}
\ tan ^ {2} x &=3\ tan x & & &\\
\ tan ^ {2} x-3\ tan x &=0 & & & &\
\ tan x (\ tan x-3) &=0 & & &\
\ tan x &=0\ qquad\ text {o}\ quad &\ tan x&=3\\
x &=0,\ pi & amp; x&=1.25
\ end {alineado}\)

Ejemplo\(\PageIndex{4}\)

Encuentra todas las soluciones para la ecuación trigonométrica\(2 \sin^2\dfrac{x}{4}−3\cos \dfrac{x}{4}=0\) a lo largo del intervalo\([0,2\pi )\).

Solución

\(2\sin^2 \dfrac{x}{4}−3\cos \dfrac{x}{4}=0\)

\ (\ begin {array} {c} &\ qquad\ qquad\ quad 2\ izquierda (1-\ cos ^ {2}\ dfrac {x} {4}\ derecha) -3\ cos\ dfrac {x} {4} =0\\
&\ qquad\ qquad\ quad 2-2\ cos ^ {2}\ dfrac {x} {4} -3\ cos\ dfrac {x} {4} =0\\
&\ qquad\ qquad\ quad 2\ cos ^ {2}\ dfrac {x} {4} +3\ cos\ dfrac {x} {4} -2=0\\
& amp;\ qquad\ qquad\ quad\ izquierda (2\ cos\ dfrac {x} {4} -1\ derecha)\ izquierda (\ cos\ dfrac {x} {4} +2\ derecha) =0\ end {array}\\ begin {alineado} &\ swarrow &\ searrow &\ searrow &\ 2\ cos\ dfrac {x} {4} -1&=0 &\ texto {o}\ quad\ cos\ dfrac {x} {4} +2&=0\\ 2\ cos\ dfrac {x} {4} &=1 &\ cos\ dfrac {x} {4} &=-2\\\ cos \ dfrac {x} {4} &=\ dfrac {1} {2} & &\\ dfrac {x} {4} =\ dfrac {\ pi} {3}\ quad\ texto {o}\ quad&\ dfrac {5\ pi} {3} &&\ x=\ dfrac {4\ pi} {3}\ quad\ texto o {}\ quad&\ dfrac {20\ pi} {3} &&\ end {alineado}\)

\(\dfrac{20\pi}{3}\)se elimina como solución porque está fuera del rango y no\(\cos x^4=−2\) generará ninguna solución porque\(−2\) está fuera del rango del coseno. Por lo tanto, la única solución es\(\dfrac{4\pi}{3}\).

Revisar

Resuelve cada ecuación\(x\) durante el intervalo\([0,2\pi )\).

1. \(\cos^2 (x)+2 \cos(x)+1=0\)
2. \(1−2\sin (x)+\sin^2 (x)=0\)
3. \(2\cos (x) \sin (x)−\cos(x)=0\)
4. \(\sin (x) \tan^2 (x)−\sin (x) =0\)
5. \(\sec^2 (x)=4\)
6. \(\sin^2 (x)−2\sin (x) =0\)
7. \(3\sin (x) =2\cos^2 (x)\)
8. \(2\sin^2 (x)+3\sin (x) =2\)
9. \(\tan(x) \sin^2 (x)=\tan(x)\)
10. \(2\sin^2 (x)+\sin (x) =1\)
11. \(2\cos(x)\tan(x)−\tan (x)=0\)
12. \(\sin^2 (x)+\sin (x) =2\)
13. \(\tan(x)(2 \cos^2 (x)+3\cos(x)−2)=0\)
14. \(\sin^2 (x)+1=2\sin (x)\)
15. \(2\cos^2 (x)−3\cos (x)=2\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.4.

El vocabulario

Término	Definición
Factoring	Factorización es el proceso de dividir un número o expresión en un producto de números o expresiones más pequeños.

Recursos adicionales

Video: Ejemplo: Resolver una ecuación trigonométrica por factorización

Práctica: Ecuaciones trigonométricas mediante factorización