4.1.10: Aplicaciones de la Ley de Cosinos
- Page ID
- 107638
Relación entre los tres lados y un ángulo para triángulos no rectos.
Mientras ayudabas a tu mamá a hornear algún día, ustedes dos tienen una idea inusual. Quieres cortar el pastel en trozos, y luego congelar sobre la superficie de cada pieza. Empiezas cortando una rebanada del pastel, pero no cortas la rebanada correctamente. Termina siendo un triángulo oblicuo, con un lado de 5 pulgadas, un lado de 6 pulgadas, y un ángulo de\(70^{\circ} \) entre los lados que midió. ¿Puedes ayudar a tu mamá a determinar la longitud del tercer lado, para que pueda averiguar cuánto glaseado apagar?
Ley de Cosinos
La Ley de Cosines es una fantástica extensión del Teorema de Pitágoras a los triángulos oblicuos. En esta sección, mostramos algunas formas interesantes de utilizar esta fórmula para analizar situaciones del mundo real.
Echemos un vistazo a algunos problemas donde utilizamos la Ley de Cosinos.
1. En una partida de billar, un jugador deberá meter la bola ocho en el bolsillo inferior izquierdo de la mesa. Actualmente, la bola ocho se encuentra a 6.8 pies de distancia del bolsillo inferior izquierdo. No obstante, debido a la posición de la bola blanca, debe tomar el tiro del parachoques lateral derecho. Si la bola ocho está a 2.1 pies de distancia del lugar en el parachoques necesita golpear y forma un\(168^{\circ} \) ángulo con el bolsillo y el punto en el parachoques, ¿en qué ángulo necesita la pelota para salir del parachoques?
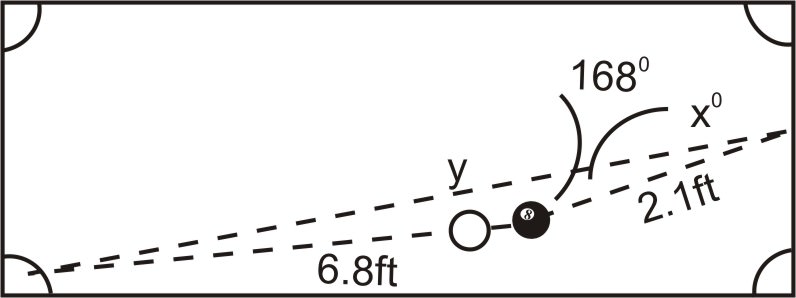
Nota: Esto es en realidad un truco realizado haciendo girar la bola ocho, y la bola ocho en realidad no viajará en trayectorias en línea recta. No obstante, para simplificar el problema, supongamos que viaja en líneas rectas.
En el escenario anterior, tenemos el caso SAS, lo que significa que necesitamos usar la Ley de Cosinos para comenzar a resolver este problema. La Ley de Cosinos nos permitirá encontrar la distancia desde el punto en el parachoques hasta el bolsillo (y). Una vez que conocemos y, podemos usar la Ley de los Sinos para encontrar el ángulo (X).
\(\begin{aligned} y^2 &=6.8^2+2.1^2−2(6.8)(2.1) \cos 168^{\circ} \\ y^2 &=78.59\\ y&=8.86 \text{ feet} \end{aligned}\)
2. La distancia desde el punto en el parachoques hasta el bolsillo es de 8.86 pies. Ahora podemos usar esta distancia y la Ley de Sines para encontrar el ángulo X. Ya que estamos encontrando un ángulo, nos encontramos ante el caso SSA, lo que significa que no podríamos tener solución, una solución, o dos soluciones. Sin embargo, como conocemos los tres lados, este problema solo dará una solución.
\ (\ begin {alineado}
\ dfrac {\ sin 168^ {\ circ}} {8.86} &=\ dfrac {\ sin X} {6.8}\
\ dfrac {6.8\ sin 168^ {\ circ}} {8.86} &=\ sin X\
0.1596 &\ approx\ sin B\
\ ángulo B &=8.77^ {\ circ}
\ fin {alineado}\)
En el ejemplo anterior, vimos cómo podemos utilizar la Ley de los Sinos y la Ley de los Cosinos juntos para resolver un problema que involucra el caso SSA. En esta sección, veremos situaciones en las que podemos utilizar no sólo la Ley de los Senos y la Ley de los Cosinos, sino también el Teorema de Pitágoras y las relaciones trigonométricas. También veremos otra aplicación del mundo real que involucra el caso SSA.
3. Tres científicos están instalando equipos para recopilar datos sobre una montaña local. La Persona 1 se encuentra a 131,5 metros de la Persona 2, que está a 67.8 metros de la Persona 3. La persona 1 se encuentra a 72.6 metros de la montaña. Las montañas forman un\(103^{\circ} \) ángulo con la Persona 1 y la Persona 3, mientras que la Persona 2 forma un\(92.7^{\circ} \) ángulo con la Persona 1 y la Persona 3. Encuentra el ángulo formado por la Persona 3 con la Persona 1 y la montaña.
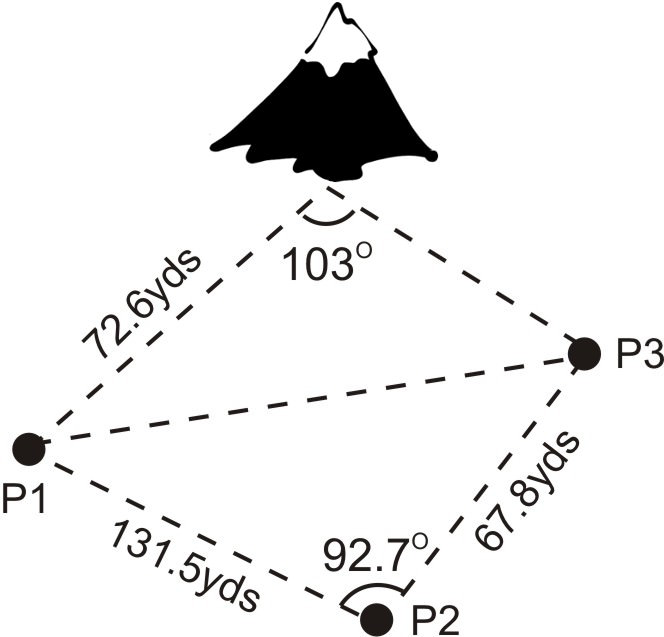
En el triángulo formado por las tres personas, conocemos dos lados y el ángulo incluido (SAS). Podemos usar la Ley de Cosinos para encontrar el lado restante de este triángulo, al que llamaremos x. Una vez que conozcamos x, haremos dos lados y el ángulo no incluido (SSA) en el triángulo formado por la Persona 1, la Persona 2, y la montaña. Entonces podremos utilizar la Ley de los Sinos para calcular el ángulo formado por la Persona 3 con la Persona 1 y la montaña, a la que nos referiremos como\(Y\).
Para encontrar\(x\):
\(\begin{aligned} x^2 &=131.5^2+67.8^2−2(131.5)(67.8)\cos 92.7\\ x^2 &=22729.06397\\ x&=150.8 \text{ yds} \end{aligned}\)
Ahora que sabemos\(x=150.8\), podemos usar la Ley de los Sinos para encontrar\(Y\). Dado que este es el caso de la SSA, necesitamos verificar para ver si no tendremos solución, una solución o dos soluciones. Ya que\(150.8>72.6\), sabemos que vamos a tener una sola solución a este problema.
\ (\ comenzar {alineado}
\ dfrac {\ sin 103} {150.8} &=\ dfrac {\ sin Y} {72.6}\
\ dfrac {72.6\ sin 103} {150.8} &=\ sin Y\\
0.4690932805 &=\ sin Y\
28.0 &\ approx\ ángulo Y
\ final {alineado}\)
4. Katie está construyendo una cometa con forma de triángulo.
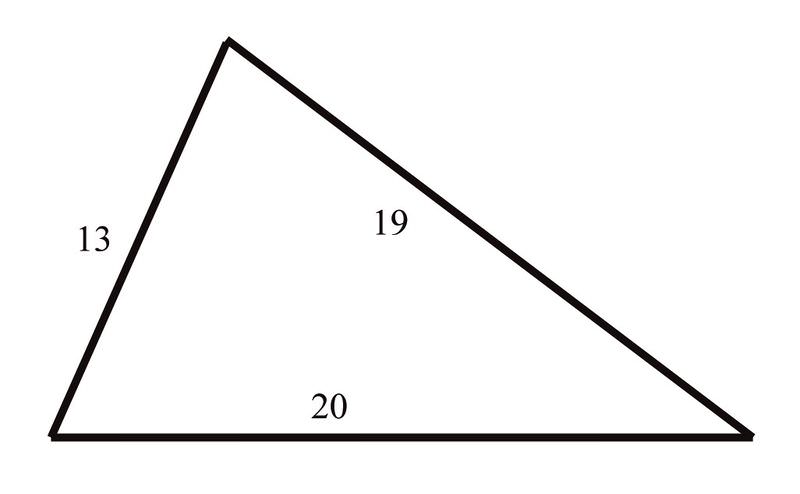
Ella sabe que las longitudes de los lados son a = 13 pulgadas, b = 20 pulgadas y c = 19 pulgadas. ¿Cuál es la medida del ángulo entre lados ""\(a\) "y"\(b\) “?
Ya que conoce la longitud de cada uno de los lados del triángulo, puede utilizar la Ley de Cosinos para encontrar el ángulo deseado:
\ (\ begin {alineado}
c^ {2} &=a^ {2} +b^ {2} -2 (a) (b)\ cos C\\
19^ {2} &=13^ {2} +20^ {2} - (2) (13) (20)\ cos C\\
361 &=169+400-520\ cos C\\
-208 &=-520\ cos C\\
\ cos C &=0.4\\
C &\ aproximadamente 66.42^ {\ circ}
\ end {alineado}\)
Antes, se le pidió que determinara la longitud del tercer lado.
Solución
Puedes usar la Ley de Cosinos para ayudar a tu mamá a averiguar la longitud del tercer lado en el trozo de pastel:
\ (\ begin {alineado}
c^ {2} &=a^ {2} +b^ {2} -2 a b\ cos C\\
c^ {2} &=5^ {2} +6^ {2} + (2) (5) (6)\ cos 70^ {\ circ}\\
c^ {2} &=25+36+60 (.342)\\
c^ {2}} &=81.52\\
c &\ aprox 9.03
\ final {alineado}\)
El trozo de pastel mide poco más de 9 pulgadas de largo.
Estás cortando un triángulo para la escuela que se ve así:
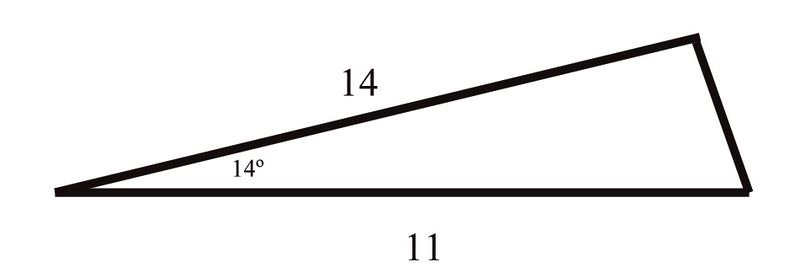
Encuentra lado\(c\) (que es el lado opuesto al\(14^{\circ} \) ángulo) y\(\angle B \) (que es el ángulo opuesto al lado que tiene una longitud de 14).
Solución
Sabes que dos de los lados tienen longitudes de 11 y 14 pulgadas, y que el ángulo entre ellos es\(14^{\circ} \). Puedes usar esto para encontrar la longitud del tercer lado:
\ (\ begin {alineado}
c^ {2} &=a^ {2} +b^ {2} -2 a b\ cos\ theta\\
c^ {2} &=121+196- (2) (11) (14) (.97)\\
c^ {2} &=121+196-307.384\\
c^ {2} &=9.16\
c&=3.03
\ fin {alineado}\)
Y con esto puedes usar la Ley de Sines para resolver por el ángulo desconocido:
\ (\ begin {alineado}
\ dfrac {\ sin 14^ {\ circ}} {3.03} &=\ dfrac {\ sin B} {11}\
\ sin B&=\ dfrac {11\ sin 14^ {\ circ}} {3.03}\
\ sin B&=.878\\
B&=\ sin ^ {-1} (.0307) =61.43^ {\ circ}
\ final {alineado}\)
Mientras haces senderismo un día caminas 2 millas en una dirección. Luego giras\(110^{\circ} \) a la izquierda y caminas 3 millas más. Tu camino se ve así:
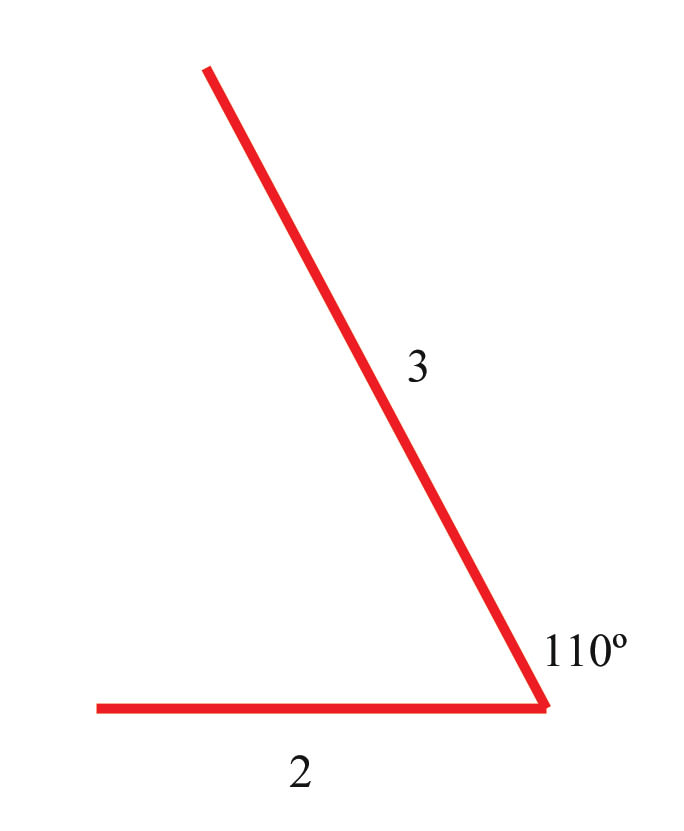
Solución
Cuando vuelvas a girar a la izquierda para completar el triángulo que es tu ruta de senderismo para el día, ¿hasta dónde tendrás que caminar para completar el tercer lado? ¿Qué ángulo debes girar antes de comenzar a caminar de regreso a casa?
Ya que conoces las longitudes de dos de las patas del triángulo, junto con el ángulo entre ellas, puedes usar la Ley de Cosinos para averiguar hasta dónde tendrás que caminar por la tercera etapa:
\ (\ begin {alineado}
c^ {2} &=a^ {2} +b^ {2} +2 a b\ cos 70^ {\ circ}\\
c^ {2} &=4+1+ (2) (2) (1) (.342)\\
c^ {2} &=6.368\
c&=\ sqrt {6.368}\ aproximadamente 2.52
\ fin {alineado}\)
Ahora tienes suficiente información para resolver para el ángulo interior del triángulo que es complementario al ángulo que necesitas girar:
\ (\ comenzar {alineado}
\ dfrac {\ sin A} {a} &=\ dfrac {\ sin B} {b}\
\ dfrac {\ sin 70^ {\ circ}} {2.52} &=\ dfrac {\ sin B} {2}\
\ sin B&=\ dfrac {2\ sin 70^ {\ circ}} {2.52} =\ dfrac {1.879} {2.52} =.746\\
B&=\ sin ^ {-1} (.746) =48.25^ {\ circ}
\ end { alineado}\)
El ángulo\(48.25^{\circ} \) es el ángulo interior del triángulo. Por lo que debes girar\(90^{\circ} +(90^{\circ} −48.25^{\circ} )=90^{\circ} +41.75^{\circ} =131.75^{\circ} \) a la izquierda antes de comenzar a casa.
Se está utilizando un soporte en un sitio de construcción para sostener una tabla para que forme un triángulo, así:
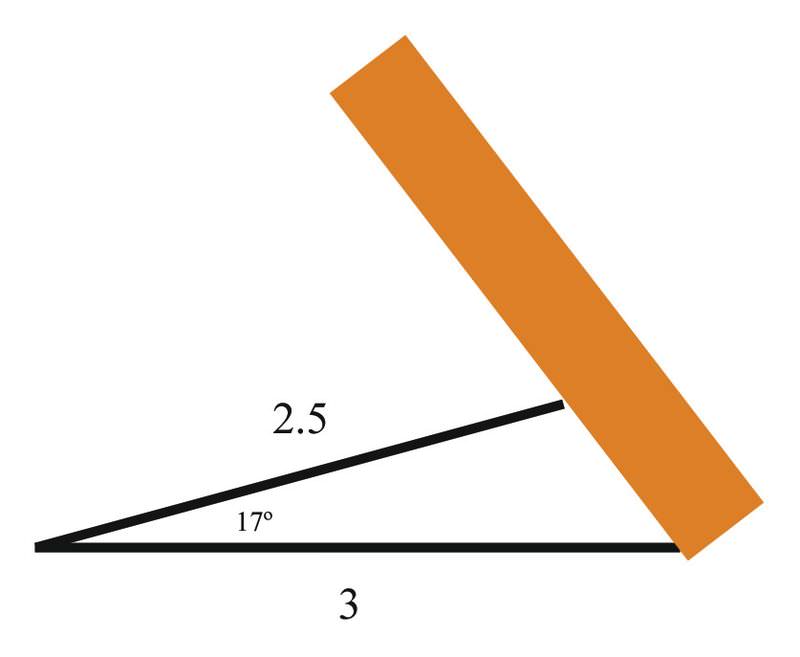
Solución
Si el ángulo entre el soporte y el suelo es\(17^{\circ} \), la longitud del soporte es de 2.5 metros, y la distancia entre donde el tablero toca el suelo y el fondo del soporte es de 3 metros, ¿a qué distancia a lo largo del tablero está tocando el soporte? ¿Cuál es el ángulo entre el tablero y el suelo?
Primero debes usar la Ley de Cosinos para resolver por la distancia desde el suelo hasta donde el soporte se encuentra con el tablero:
\(\begin{aligned} c^2&=a^2+b^2+2ab \cos 17^{\circ} \\ c^2&=6.25+9+(2)(2.5)(3)\cos 17^{\circ} \\ c^2&=6.25+9+(2)(2.5)(3)(.956) \\ c^2&=26.722 \\ c&\approx 5.17 \end{aligned}\)
Y ahora puedes usar la Ley de Sines:
\ (\ comenzar {alineado}
\ dfrac {\ sin A} {a} &=\ dfrac {\ sin B} {b}\
\ dfrac {\ sin 17^ {\ circ}} {5.17} &=\ dfrac {\ sin B} {2.5}\
\ sin B &=\ dfrac {2.5\ sin 17^ {\ circ}} {5.17} =.1414\\
B&=\ sin ^ {-1} (.1414) =8.129^ {\ circ}
\ final {alineado}\)
Revisar
En\(\Delta ABC\),\(a=12\),\(b=15\), y\(c=20\).
- Encontrar\(m\angle A\).
- Encontrar\(m\angle B\).
- Encontrar\(m\angle C\).
En\(\Delta DEF\),\(d=25\),\(e=13\), y\(f=16\).
- Encontrar\(m\angle D\).
- Encontrar\(m\angle E\).
- Encontrar\(m\angle F\).
En\(\Delta KBP\),\(k=19\),\(\angle B=61^{\circ} \), y\(p=12\).
- Encuentra la longitud de\(b\).
- Encontrar\(m\angle K\).
- Encontrar\(m\angle P\).
- Mientras caminas un día caminas 5 millas hacia el este, luego giras a la izquierda y caminas 3 millas más\(30^{\circ} \) al oeste del norte. En este punto quieres regresar a casa. ¿A qué distancia estás de casa si caminaras en línea recta?
- Un paralelogramo tiene lados de 20 y 31 pies, y un ángulo de\(46^{\circ} \). Encuentra la longitud de la diagonal más larga del paralelogramo.
- Dirk quiere encontrar la longitud de un edificio largo de un lado (punto\(A\)) al otro (punto\(B\)). Se encuentra afuera del edificio (en el punto\(C\)), donde está a 500 pies del punto\(A\) y 220 pies del punto\(B\). El ángulo a\(C\) es\(94^{\circ} \). Encuentra la longitud del edificio.
Determinar si cada triángulo es posible o no.
- \(a=12\),\(b=15\),\(c=10\)
- \(a=1\),\(b=5\),\(c=4\)
- \(\angle A=32^{\circ}\),\(a=8\),\(b=10\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.11.
El vocabulario
| Término | Definición |
|---|---|
| Ángulo incluido | El ángulo incluido en un triángulo es el ángulo entre dos lados conocidos. |
| ley de cosenos | La ley de los cosenos es una norma que relaciona los lados de un triángulo con el coseno de uno de sus ángulos. La ley de los cosenos establece que\(c^2=a^2+b^2−2ab\cos C\), dónde\(C\) está el ángulo a través de lado\(c\). |
| SAS | SAS significa lado, ángulo, lado, y se refiere al hecho de que se conocen dos lados y el ángulo incluido de un triángulo. |
| SSS | SSS significa lado, lado, lado y se refiere al hecho de que los tres lados de un triángulo son conocidos en un problema. |
Recursos adicionales
Video: Resolviendo triángulos u\ sin g la Ley de los Cosinos - Ejemplo 1
Práctica: Aplicaciones de la Ley de Cosinos