1.5: Evaluar límites usando sustitución
- Page ID
- 105953
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encontrar límites para la gran mayoría de puntos para una función dada es tan simple como sustituir el número que x se acerca en la función. Dado que esto convierte la evaluación de límites en una sustitución a nivel álgebra, la mayoría de las preguntas que involucran límites se centran en los casos en los que la sustitución no funciona. ¿Cómo se puede decidir si la sustitución es una herramienta analítica adecuada para encontrar un límite?
Uso de la sustitución para buscar límites
Encontrar un límite analíticamente significa encontrar el límite usando medias algebraicas. Para evaluar muchos límites, se puede sustituir el valor que x se acerca en la función y evaluar el resultado. Esto funciona perfectamente cuando no hay agujeros o asíntotas en ese valor x particular. Puedes estar seguro de que este método funciona siempre y cuando no termines dividiéndolo por cero cuando sustituyas.
Si la función f (x) no tiene agujeros o asíntota en x=a entonces:
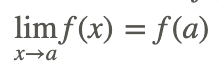
Ocasionalmente habrá un agujero en x=a El límite en este caso es la altura de la función si el agujero no existió. En otras palabras, si la función es una expresión racional con factores que pueden cancelarse, cancelar el término algebraicamente y luego sustituirla en la expresión resultante. Si no se pueden cancelar factores, podría ser que el límite no exista en ese momento debido a asíntotas.
Mira los siguientes dos límites:
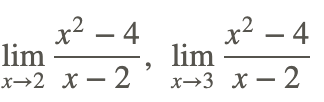
El límite de la izquierda no se puede evaluar por sustitución directa porque si se sustituye 2 en, entonces terminas dividiendo por cero.El límite de la derecha se puede evaluar usando sustitución directa porque el agujero existe en x=2 no x=3. Así, el límite es:
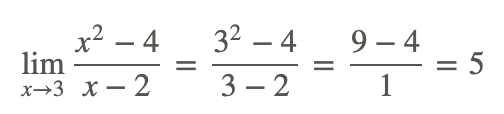
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó cómo determinar si debería usar la sustitución para resolver un límite. Para decidir si la sustitución es un primer paso apropiado siempre puedes probarla. Sabrás que no funcionará si terminas intentando evaluar una expresión con un denominador igual a cero. Si esto sucede, regrese e intente factografiar y cancelar, y luego intente sustituirlo de nuevo.
Ejemplo 2
Evalúe el siguiente límite cancelando primero y luego usando la sustitución.
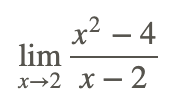
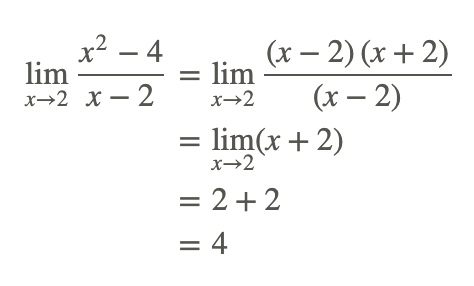
Ejemplo 3
Evalúe analíticamente el siguiente límite:
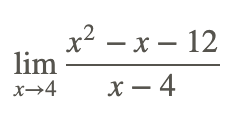
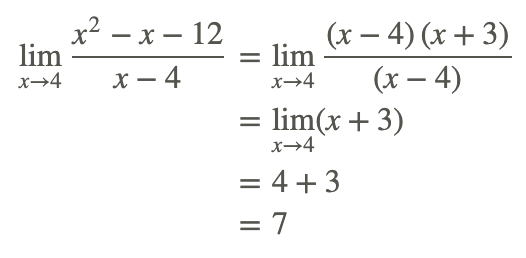
Ejemplo 4
Evaluar analíticamente el siguiente límite.
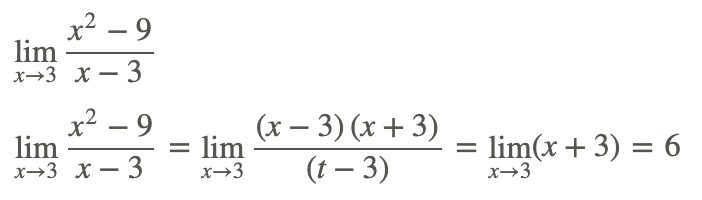
Ejemplo 5
Evaluar analíticamente el siguiente límite.
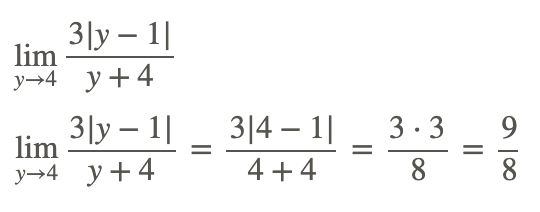
Revisar
Evaluar analíticamente los siguientes límites.
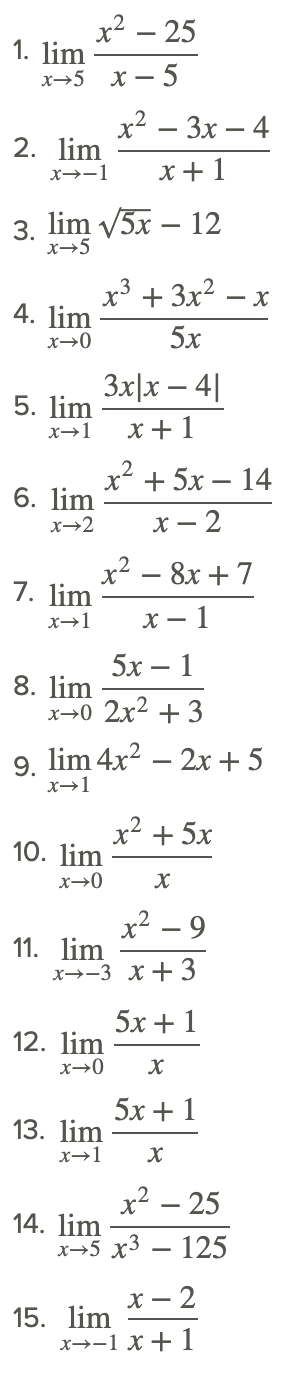
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 14.4.
vocabulario
| Término | Definición |
|---|---|
| analíticamente | Una forma de evaluar un límite analíticamente es mediante sustitución. La sustitución es un método de determinación de límites donde el valor que x se aproxima se sustituye en la función y se evalúa el resultado. |
| Asíntotas | Una asíntota es una línea en la gráfica de una función que representa un valor hacia el que la función puede acercarse, pero no alcanza (con ciertas excepciones). |
| Agujero | Existe un agujero en la gráfica de una función racional en cualquier valor de entrada que haga que tanto el numerador como el denominador de la función sean iguales a cero. |
| límite | Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado. |
Recursos adicionales
Práctica: Evaluar límites usando sustitución
Mundo real: Los límites de la tolerancia