4.1: Distribuciones normales
- Page ID
- 150978
La distribución normal es la distribución más importante y más utilizada en la estadística. A veces se le llama la “curva de campana”, aunque las cualidades tonales de tal campana serían menos que agradables. También se le llama la “curva gaussiana” de la distribución gaussiana después del matemático Karl Friedrich Gauss.
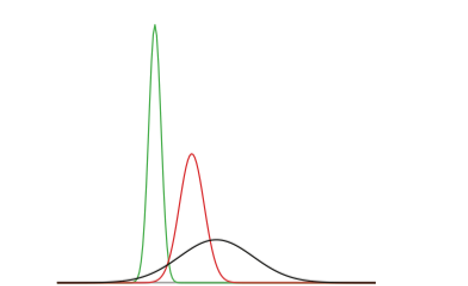
Estrictamente hablando, no es correcto hablar de “la distribución normal” ya que hay muchas distribuciones normales. Las distribuciones normales pueden diferir en sus medias y en sus desviaciones estándar. La Figura 1 muestra tres distribuciones normales. La distribución verde (más a la izquierda) tiene una media de -3 y una desviación estándar de 0.5, la distribución en rojo (la distribución media) tiene una media de 0 y una desviación estándar de 1, y la distribución en negro (más a la derecha) tiene una media de 2 y una desviación estándar de 3. Estas así como todas las demás distribuciones normales son simétricas con relativamente más valores en el centro de la distribución y relativamente pocos en las colas. Lo que es consistente en toda la distribución normal es la forma y la proporción de puntuaciones dentro de una distancia dada a lo largo del eje x. Nos centraremos en la Distribución Normal Estándar (también conocida como Distribución Normal Unitaria), que tiene una media de 0 y una desviación estándar de 1 (es decir, la distribución roja en la Figura\(\PageIndex{1}\)).
A continuación se enumeran siete características de las distribuciones normales.
- Las distribuciones normales son simétricas alrededor de su media.
- La media, la mediana y el modo de una distribución normal son iguales.
- El área bajo la curva normal es igual a 1.0.
- Las distribuciones normales son más densas en el centro y menos densas en las colas.
- Las distribuciones normales se definen por dos parámetros, la media (\(μ\)) y la desviación estándar (\(σ\)).
- El 68% del área de una distribución normal se encuentra dentro de una desviación estándar de la media.
- Aproximadamente el 95% del área de una distribución normal se encuentra dentro de dos desviaciones estándar de la media.
Estas propiedades nos permiten usar la distribución normal para entender cómo las puntuaciones se relacionan entre sí dentro y a través de una distribución. Pero primero, necesitamos aprender a calcular la puntuación estandarizada que a conformar una distribución normal estándar.


