4.2: Puntuaciones Z
- Page ID
- 150972
A\(z\) -score es una versión estandarizada de una puntuación bruta (\(x\)) que da información sobre la ubicación relativa de esa puntuación dentro de su distribución. La fórmula para convertir una puntuación sin procesar en una\(z\) puntuación -score es:
\[z=\dfrac{x-\mu}{\sigma} \]
para valores de una población y para valores de una muestra:
\[z=\dfrac{x-\overline{X}}{s} \]
Como puede ver,\(z\) -scores combinan información sobre dónde se encuentra la distribución (la media/centro) con qué tan amplia es la distribución (la desviación/propagación estándar) para interpretar una puntuación en bruto (\(x\)). Específicamente,\(z\) -scores nos dirá qué tan lejos está el puntaje de la media en unidades de desviaciones estándar y en qué dirección.
El valor de una\(z\) -score tiene dos partes: el signo (positivo o negativo) y la magnitud (el número real). El signo del\(z\) -score te indica en qué mitad de la distribución cae el puntaje z: un signo positivo (o ningún signo) indica que el puntaje está por encima de la media y en el lado derecho o extremo superior de la distribución, y un signo negativo te indica que la puntuación está por debajo de la media y en el lado izquierdo o extremo inferior de la distribución. La magnitud del número te indica, en unidades de desviaciones estándar, qué tan lejos está la puntuación del centro o media. La magnitud puede tomar cualquier valor entre infinito negativo y positivo, pero por razones veremos pronto, generalmente caen entre -3 y 3.
Veamos algunos ejemplos. Un valor\(z\) -score de -1.0 nos dice que esta puntuación z es 1 desviación estándar (debido a la magnitud 1.0) por debajo (por el signo negativo) de la media. De igual manera, un valor\(z\) -score de 1.0 nos indica que esta\(z\) -score es 1 desviación estándar por encima de la media. Así, estas dos puntuaciones se encuentran a la misma distancia de la media pero en direcciones opuestas. Una\(z\) puntuación -2.5 es dos desviaciones estándar y media por debajo de la media y, por lo tanto, está más lejos del centro que ambas puntuaciones anteriores, y una\(z\) puntuación -de 0.25 está más cerca que todas las anteriores. En la Unidad 2 aprenderemos a formalizar la distinción entre lo que consideramos “cercano” al centro o “lejos” del centro. Por ahora, usaremos un corte aproximado de 1.5 desviaciones estándar en cualquier dirección como la diferencia entre las puntuaciones cercanas (aquellas dentro de 1.5 desviaciones estándar o entre\(z\) = -1.5 y\(z\) = 1.5) y las puntuaciones extremas (aquellas más alejadas de 1.5 desviaciones estándar, por debajo de\(z\) = -1.5 o superiores \(z\)= 1.5).
También podemos convertir los puntajes brutos en\(z\) -scores para tener una mejor idea de en qué parte de la distribución caen esos puntajes. Digamos que obtenemos una puntuación de 68 en un examen. Puede que nos decepcione haber anotado tan bajo, pero quizás solo fue un examen muy duro. Tener información sobre la distribución de todos los puntajes en la clase sería útil para poner alguna perspectiva sobre la nuestra. Nos enteramos de que la clase obtuvo una puntuación promedio de 54 con una desviación estándar de 8. Para conocer nuestra ubicación relativa dentro de esta distribución, simplemente convertimos nuestro puntaje de prueba en un\(z\) puntaje -score.
\[z=\dfrac{X-\mu}{\sigma}=\frac{68-54}{8}=1.75 \nonumber \]
Encontramos que estamos 1.75 desviaciones estándar por encima de la media, por encima de nuestro corte aproximado para cerca y lejos. De repente nuestro 68 se ve bastante bien!
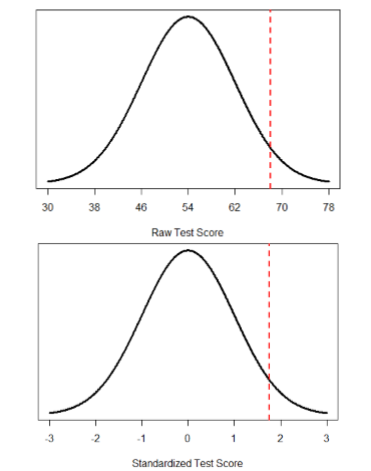
La figura\(\PageIndex{1}\) muestra tanto el puntaje bruto como el\(z\) puntaje -score en sus respectivas distribuciones. Observe que la línea roja que indica dónde se encuentra cada puntaje está en el mismo punto relativo para ambos. Esto se debe a que transformar una partitura cruda en una\(z\) -score no cambia su ubicación relativa, solo facilita saber con precisión dónde se encuentra.
\(Z\)-scores también son útiles para comparar puntuaciones de diferentes distribuciones. Digamos que tomamos el SAT y puntamos 501 tanto en las secciones de matemáticas como de lectura crítica. ¿Eso significa que nos fue igual de bien en ambos? Las puntuaciones en la parte matemática se distribuyen normalmente con una media de 511 y una desviación estándar de 120, por lo que nuestra\(z\) puntuación en la sección de matemáticas es
\[z_{math}=\dfrac{501-511}{120}=-0.08 \nonumber \]
que está ligeramente por debajo del promedio (tenga en cuenta que el uso de “matemáticas” como subíndice; los subíndices se utilizan al presentar múltiples versiones de una misma estadística para saber cuál es cuál y no tienen relación con el cálculo real). La sección de lectura crítica tiene una media de 495 y una desviación estándar de 116, por lo que
\[z_{C R}=\frac{501-495}{116}=0.05 \nonumber \]
Entonces, a pesar de que estábamos casi exactamente promedio en ambas pruebas, lo hicimos un poco mejor en la porción de lectura crítica en relación con otras personas.
Por último,\(z\) -scores son increíblemente útiles si necesitamos combinar información de diferentes medidas que están en diferentes escalas. Digamos que le damos a un conjunto de empleados una serie de pruebas sobre cosas como el conocimiento laboral, la personalidad y el liderazgo. Es posible que queramos combinarlos en una sola puntuación que podamos usar para calificar a los empleados para su desarrollo o promoción, pero mira lo que sucede cuando tomamos el promedio de puntajes brutos de diferentes escalas, como se muestra en la Tabla\(\PageIndex{1}\):
| Puntajes Raw | Conocimientos laborales (0 — 100) | Personalidad (1 —5) | Liderazgo (1 — 5) | Promedio |
|---|---|---|---|---|
| Empleado 1 | 98 | 4.2 | 1.1 | 34.43 |
| Empleado 2 | 96 | 3.1 | 4.5 | 34.53 |
| Empleado 3 | 97 | 2.9 | 3.6 | 34.50 |
Debido a que los puntajes de conocimiento laboral eran tan grandes y los puntajes fueron tan similares, superaron a los otros puntajes y eliminaron casi toda la variabilidad en el promedio. Sin embargo, si estandarizamos estos puntajes en\(z\) -scores, nuestros promedios conservan más variabilidad y es más fácil evaluar las diferencias entre empleados, como se muestra en la Tabla\(\PageIndex{2}\).
| \(z\)-Puntuaciones | Conocimientos laborales (0 — 100) | Personalidad (1 —5) | Liderazgo (1 — 5) | Promedio |
|---|---|---|---|---|
| \ (z\) -Partituras” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px ; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-right width:1px; border-right width:1px; border-right color superior:rgb ( 204, 204, 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; overflow-wrap:break-word; padding-bottom:1em; padding-izquierda:1em; padding-derecha:1em; padding-top:1em; text-align:center; vertical-align:top; ">Employee 1 | 1.00 | 1.14 | -1.12 | 0.34 |
| \ (z\) -Partituras” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-color:rgb (204, 204); border-bottom-color:rgb (204, 204); border-abajo-inferior estilo:discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-source:none; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-right-style:rgb (204, 204); border-right-style:rgb (204, 204); border-right-style:rgb (204, 204); :discontinuo; borde- ancho derecho:1px; borde superior-color:rgb (204, 204); borde superior-estilo:discontinuo; borde superior-ancho:1px; tamaño-caja:border-box; desbordamiento-envoltura:break-word; padding-bottom:1em; padding-izquierda:1em; padding-derecha:1em; padding-top:1em; text-align:center; vertical-align:top; ">Empleado 2 | -1.00 | -0.43 | 0.81 | -0.20 |
| \ (z\) -Partituras” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (243, 251, 255); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-color:rgb (204, 204); border-bottom-color:rgb (204, 204); border-abajo-inferior estilo:discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-source:none; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-right-style:rgb (204, 204); border-right-style:rgb (204, 204); border-right-style:rgb (204, 204); :discontinuo; borde- ancho derecho:1px; borde superior-color:rgb (204, 204); borde superior-estilo:discontinuo; borde superior-ancho:1px; tamaño-caja:border-box; desbordamiento-envoltura:break-word; padding-bottom:1em; padding-izquierda:1em; padding-derecha:1em; padding-top:1em; text-align:center; vertical-align:top; ">Empleado 3 | 0.00 | -0.71 | 0.30 | -0.14 |
Establecer la escala de una distribución
Otra característica conveniente de\(z\) -scores es que se pueden convertir en cualquier “escala” que nos gustaría. Aquí, el término escala significa qué tan separados están los puntajes (su difusión) y dónde se encuentran (su tendencia central). Esto puede ser muy útil si no queremos trabajar con números negativos o si tenemos un rango específico nos gustaría presentar. Las fórmulas para transformarse\(z\) a\(x\) son:
\[x=z \sigma+\mu \]
para una población y
\[x=z s+\overline{X} \]
para una muestra. Observe que estos son solo reordenamientos simples de las fórmulas originales para calcular\(z\) a partir de puntajes brutos.
Digamos que creamos una nueva medida de inteligencia, y la calibración inicial encuentra que nuestras puntuaciones tienen una media de 40 y una desviación estándar de 7. Tres personas que tienen puntajes de 52, 43 y 34 quieren saber qué tan bien le fue en la medida. Podemos convertir sus puntajes brutos en\(z\) -scores:
\[\begin{aligned} z &=\dfrac{52-40}{7}=1.71 \\ z &=\dfrac{43-40}{7}=0.43 \\ z &=\dfrac{34-40}{7}=-0.80 \end{aligned} \nonumber \]
Un problema es que estas nuevas\(z\) puntuaciones no son exactamente intuitivas para muchas personas. Podemos dar a las personas información sobre su ubicación relativa en la distribución (por ejemplo, la primera persona puntuada muy por encima del promedio), o podemos traducir estos\(z\) puntajes a la métrica más familiar de puntajes de CI, que tienen una media de 100 y una desviación estándar de 16:
\[\begin{array}{l}{\mathrm{IQ}=1.71 * 16+100=127.36} \\ {\mathrm{IQ}=0.43 * 16+100=106.88} \\ {\mathrm{IQ}=-0.80 * 16+100=87.20}\end{array} \nonumber \]
También podríamos redondear estos valores a 127, 107 y 87, respectivamente, por conveniencia.


