1.9: Mediciones
- Page ID
- 152480
Objetivos de aprendizaje
- Entender lo que significa que una escala sea ordinal y su relación con escalas de intervalo.
- Determinar si un investigador puede ser engañado calculando los medios de una escala ordinal.
Instrucciones
Esto es una demostración de un tema muy complejo. Los expertos en la materia no están de acuerdo sobre cómo interpretar las diferencias en una escala ordinal, así que no se desanime si le toma un tiempo ponerse al día. En esta demostración explorarás la relación entre el intervalo y las escalas ordinales. La demostración se basa en dos marcas de productos horneados.
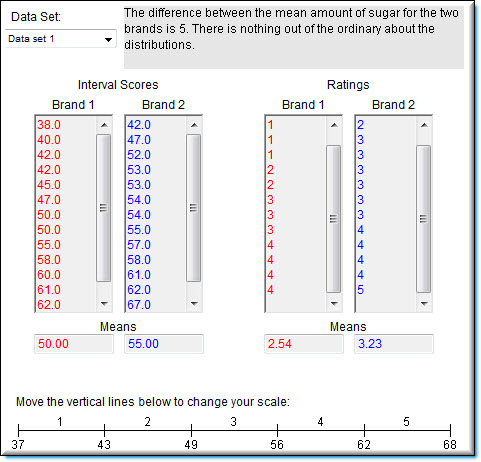
Los datos del lado izquierdo etiquetados como “puntuaciones de intervalo” muestran la cantidad de azúcar en cada uno de los\(12\) productos. La columna etiquetada "\(\text{Brand 1}\)" contiene el contenido de azúcar de cada uno de los productos de la\(12\) marca uno. La segunda columna (”\(\text{Brand 1}\) “) muestra el contenido de azúcar de los dos productos de la marca. La cantidad de azúcar se mide en una escala de intervalos.
Un evaluador prueba cada uno de los productos y los califica en una escala\(5\) de “dulzura” de punto. Las escalas de calificación suelen ser ordinales en lugar de intervalos.
La escala en la parte inferior muestra el “mapeo” del contenido de azúcar en las calificaciones. El contenido de azúcar entre\(37\) y\(43\) se\(1\) califica como, entre\(43\) y\(49, 2, etc.\) Por lo tanto, la diferencia entre una calificación de\(1\) y una calificación de\(2\) representa, en promedio una “diferencia de azúcar” de\(6\). Una diferencia entre una calificación de\(2\) y una calificación de\(3\) también representa, en promedio una “diferencia de azúcar” de\(6\). Las calificaciones originales se redondean y se muestran en una escala de intervalo. Es probable que las calificaciones del evaluador no estén en una escala de intervalo. Puede cambiar los puntos de corte entre clasificaciones moviendo las líneas verticales con el mouse. A medida que cambias estos puntos de corte, las calificaciones cambian automáticamente. Por ejemplo, podrías ver cómo serían las calificaciones si la gente no considerara algo muy dulce (calificación de\(5\)) a menos que fuera muy, muy dulce.
La cantidad media de azúcar en\(\text{Data Set 1}\) es\(50\) para la primera marca y\(55\) para la segunda marca. La conclusión obvia es que, en promedio, la segunda marca es más dulce que la primera. No obstante, finge que solo tenías las calificaciones para pasar y no estabas al tanto de las cantidades reales de azúcar. ¿Llegarías a la decisión correcta si compararas las calificaciones medias de las dos marcas? Cambiar los puntos de corte para mapear la escala de azúcar de intervalo en la escala de clasificación ordinal. ¿Algún mapeado conduce a interpretaciones incorrectas? Prueba esto con\(\text{Data Set 1}\) y con\(\text{Data Set 2}\). Trate de encontrar una situación en la que el índice de dulzura media sea mayor para\(\text{Brand 2}\) aunque la cantidad media de azúcar sea mayor para\(\text{Brand 1}\). Si encuentras tal situación, entonces has encontrado una instancia en la que el uso de los medios de datos ordinales lleva a conclusiones incorrectas. Es posible encontrar esta situación, así que mira con atención.
Ten en cuenta que en situaciones realistas, solo conoces las calificaciones y no la escala de intervalo “verdadera” que subyace a ellas. Si conocieras la escala de intervalos, la usarías.


