1.10: Distribuciones
- Page ID
- 152483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Objetivos de aprendizaje
- Definir “distribución”
- Interpretar una distribución de frecuencias
- Distinguir entre una distribución de frecuencia y una distribución de probabilidad
- Construir una distribución de frecuencia agrupada para una variable continua
- Identificar el sesgo de una distribución
- Identificar distribuciones bimodales, leptóurticas y platykurtic
Distribuciones de Variables Discretas
A recientemente comprada una bolsa de Plain M&M's contenía caramelos de seis colores diferentes. Un conteo rápido mostró que había\(55\) M&M's:\(17\) marrón,\(18\) rojo,\(7\) amarillo,\(7\) verde,\(2\) azul y\(4\) naranja. Estos recuentos se muestran a continuación en la Tabla\(\PageIndex{1}\).
| Color | Frecuencia |
|---|---|
| Marrón | 17 |
| Rojo | 18 |
| Amarillo | 7 |
| Verde | 7 |
| Azul | 2 |
| Naranja | 4 |
Esta tabla se denomina tabla de frecuencias y describe la distribución de las frecuencias de color M&M. No es sorprendente que este tipo de distribución se llame distribución de frecuencia. A menudo se muestra gráficamente una distribución de frecuencias como en la Figura\(\PageIndex{1}\).
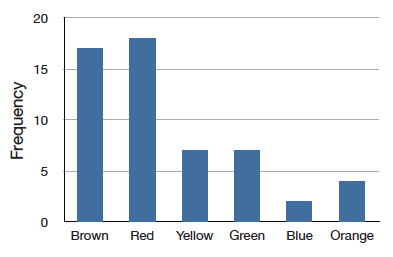
La distribución que se muestra en la Figura se\(\PageIndex{1}\) refiere solo a mi única bolsa de M&M's. Quizás te estés preguntando sobre la distribución de colores para todos los M&M's. El fabricante de M&M's proporciona alguna información sobre este asunto, pero no nos dicen exactamente cuántos M&M's de cada color han producido alguna vez. En cambio, reportan proporciones en lugar de frecuencias. La figura\(\PageIndex{2}\) muestra estas proporciones. Dado que cada M&M es uno de los seis colores familiares, las seis proporciones que se muestran en la figura se suman a uno. Llamamos a Figura\(\PageIndex{2}\) una distribución de probabilidad porque si eliges un M&M al azar, la probabilidad de obtener, digamos, un M&M marrón es igual a la proporción de M&M's que son brown (\(0.30\)).
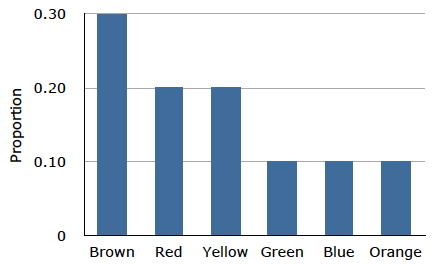
Observe que las distribuciones en Figuras\(\PageIndex{1}\) y no\(\PageIndex{2}\) son idénticas. La figura\(\PageIndex{1}\) retrata la distribución en una muestra de\(55\) M&M's. La figura\(\PageIndex{2}\) muestra las proporciones para todos los M&M's. Los factores de probabilidad que involucran las máquinas utilizadas por el fabricante introducen variaciones aleatorias en las diferentes bolsas producidas. Algunas bolsas tendrán una distribución de colores que está cerca de Figura\(\PageIndex{2}\); otras estarán más lejos.
Variables continuas
La variable “color de M&M” utilizada en este ejemplo es una variable discreta, y su distribución también se llama discreta. Extendamos ahora el concepto de una distribución a variables continuas. Los datos que se muestran en la Tabla\(\PageIndex{2}\) son los tiempos que tardó uno de nosotros (DL) en mover al ratón sobre una diana pequeña en una serie de\(20\) ensayos. Los tiempos se ordenan del más corto al más largo. La variable “tiempo para responder” es una variable continua. Con el tiempo medido con precisión (a muchos decimales), no se esperaría que dos tiempos de respuesta fueran iguales. Medir el tiempo en milisegundos (milésimas de segundo) suele ser lo suficientemente preciso como para aproximarse a una variable continua en Psicología. Como puede ver en la Tabla\(\PageIndex{2}\), medir las respuestas de DL de esta manera produjo tiempos no dos de los cuales fueron iguales. En consecuencia, una distribución de frecuencias sería poco informativa: consistiría en los\(20\) tiempos en el experimento, cada uno con una frecuencia de\(1\).
| 568 | 720 |
| 577 | 728 |
| 581 | 729 |
| 640 | 777 |
| 641 | 808 |
| 645 | 824 |
| 657 | 825 |
| 673 | 865 |
| 696 | 875 |
| 703 | 1007 |
La solución a este problema es crear una distribución de frecuencia agrupada. En una distribución de frecuencia agrupada, se tabulan las puntuaciones que se encuentran dentro de varios rangos. \(\PageIndex{3}\)El cuadro muestra una distribución de frecuencia agrupada para estos\(20\) tiempos.
| Rango | Frecuencia |
|---|---|
| 500-600 | 3 |
| 600-700 | 6 |
| 700-800 | 5 |
| 800-900 | 5 |
| 900-1000 | 0 |
| 1000-1100 | 1 |
Las distribuciones de frecuencia agrupadas pueden ser retratadas gráficamente. La figura\(\PageIndex{3}\) muestra una representación gráfica de la distribución de frecuencias en la Tabla\(\PageIndex{3}\). Este tipo de gráfico se llama histograma. Un capítulo posterior contiene una sección completa dedicada a los histogramas.
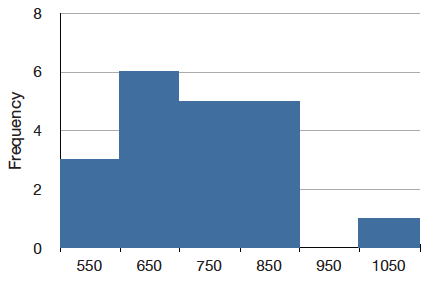
Densidades de Probabilidad
El histograma de la Figura\(\PageIndex{3}\) retrata solo los\(20\) tiempos de DL en el único experimento que realizó. Para representar la probabilidad asociada a un movimiento arbitrario (que puede tomar cualquier cantidad de tiempo positiva), debemos representar todos estos tiempos potenciales a la vez. Para ello, trazamos la distribución para la variable continua de tiempo. Las distribuciones para variables continuas se denominan distribuciones continuas. También llevan el nombre más imaginario densidad de probabilidad. Algunas densidades de probabilidad tienen particular importancia en la estadística. Una muy importante tiene forma de campana, y se llama la distribución normal. Muchos fenómenos naturales pueden aproximarse sorprendentemente bien por esta distribución. Servirá para ilustrar algunas características de todas las distribuciones continuas.
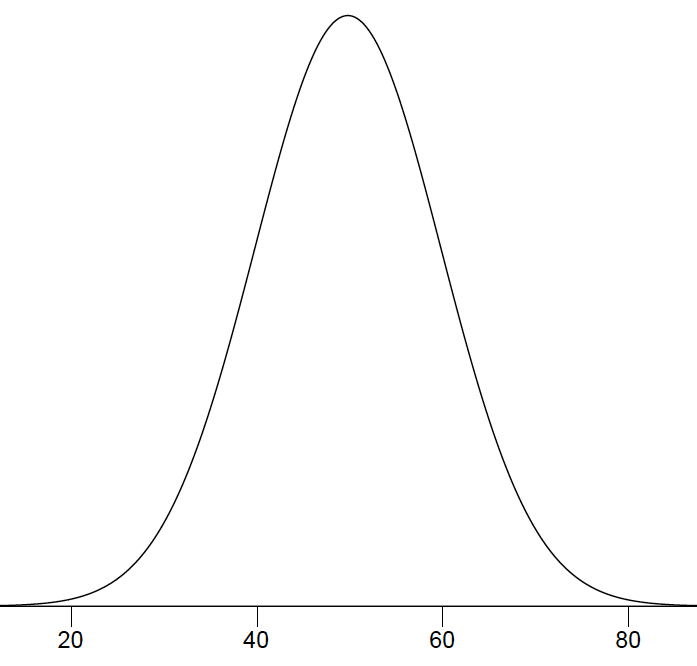
Un ejemplo de una distribución normal se muestra en la Figura\(\PageIndex{4}\). ¿Ves la “campana”? La distribución normal no representa una campana real, sin embargo, ya que las puntas izquierda y derecha se extienden indefinidamente (no podemos dibujarlas más por lo que parece que se han detenido en nuestro diagrama). El\(Y\) eje -en la distribución normal representa la “densidad de probabilidad”. Intuitivamente, muestra la posibilidad de obtener valores cercanos a los puntos correspondientes en el\(X\) eje. En la Figura\(\PageIndex{4}\), por ejemplo, la probabilidad de una observación con valor cercano\(40\) es aproximadamente la mitad de la probabilidad de una observación con valor cercano\(50\). (Para mayor información, consulte el capítulo sobre distribuciones normales.)
Aunque este texto no discute en detalle el concepto de densidad de probabilidad, se deben tener en cuenta las siguientes ideas sobre la curva que describe una distribución continua (como la distribución normal). Primero, el área bajo la curva es igual\(1\). Segundo, la probabilidad de cualquier valor exacto de\(X\) es\(0\). Finalmente, el área bajo la curva y delimitada entre dos puntos dados en el\(X\) eje es la probabilidad de que un número elegido al azar caiga entre los dos puntos. Ilustremos con los movimientos de la mano de DL. Primero, ¡la probabilidad de que su movimiento tome alguna cantidad de tiempo es una! (Excluimos la posibilidad de que no acabe nunca su gesto.) Segundo, la probabilidad de que su movimiento tome exactamente\(598.956432342346576\) milisegundos es esencialmente cero. (Podemos hacer que la probabilidad sea lo más cercana a cero al hacer que la medición del tiempo sea cada vez más precisa). Finalmente, supongamos que la probabilidad de que el movimiento de DL tome entre\(600\) y\(700\) milisegundos es de una décima parte. Entonces la distribución continua para los tiempos posibles de DL tendría una forma que coloca el área debajo\(10\%\) de la curva en la región delimitada por\(600\) y\(700\) sobre el\(X\) eje.
Formas de Distribuciones
Las distribuciones tienen diferentes formas; no todas se parecen a la distribución normal de la Figura\(\PageIndex{4}\). Por ejemplo, la densidad de probabilidad normal es mayor en el medio en comparación con sus dos colas. Otras distribuciones no necesitan tener esta característica. Incluso hay variación entre las distribuciones que llamamos “normales”. Por ejemplo, algunas distribuciones normales están más extendidas que la que se muestra en la Figura\(\PageIndex{4}\) (sus colas comienzan a golpear el\(X\) eje más lejos de la mitad de la curva, por ejemplo, en\(10\) y\(90\) si se dibujan en lugar de la Figura\(\PageIndex{4}\)). Otros están menos extendidos (sus colas podrían acercarse al\(X\) eje en\(30\) y\(70\)). Más información sobre la distribución normal se puede encontrar en un capítulo posterior completamente dedicado a ellos.
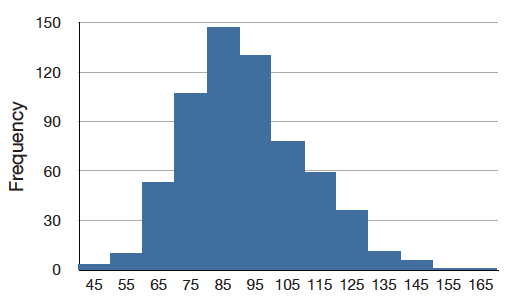
La distribución que se muestra en la Figura\(\PageIndex{4}\) es simétrica; si la doblaste en el medio, los dos lados coincidirían perfectamente. La figura\(\PageIndex{5}\) muestra la distribución discreta de las puntuaciones en una prueba de psicología. Esta distribución no es simétrica: la cola en la dirección positiva se extiende más allá de la cola en la dirección negativa. Se dice que una distribución con la cola más larga extendiéndose en la dirección positiva tiene un sesgo positivo. También se describe como “sesgada a la derecha”.
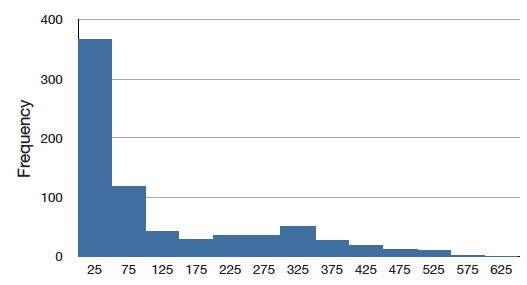
La figura\(\PageIndex{6}\) muestra los salarios de los beisbolistas de Grandes Ligas en 1974 (en miles de dólares). Esta distribución tiene un sesgo positivo extremo.
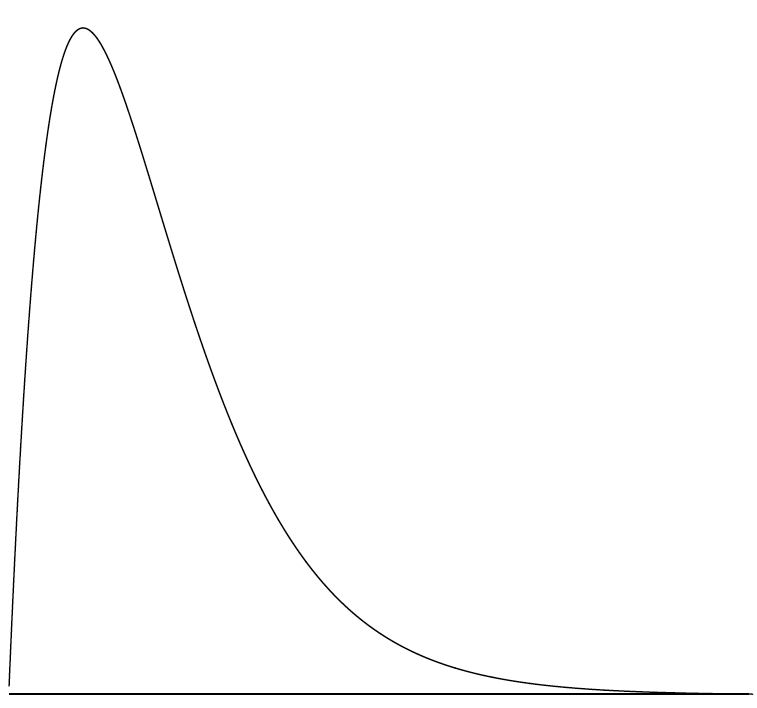
En la Figura se muestra una distribución continua con un sesgo positivo\(\PageIndex{7}\).
Aunque menos comunes, algunas distribuciones tienen un sesgo negativo. La figura\(\PageIndex{8}\) muestra las puntuaciones en un problema\(20\) de puntos en un examen de estadística. Dado que la cola de la distribución se extiende hacia la izquierda, esta distribución está sesgada hacia la izquierda.
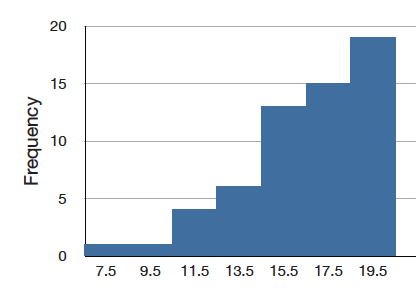
El histograma de la Figura\(\PageIndex{8}\) muestra las frecuencias de varias puntuaciones en una pregunta\(20\) de punto en una prueba estadística.
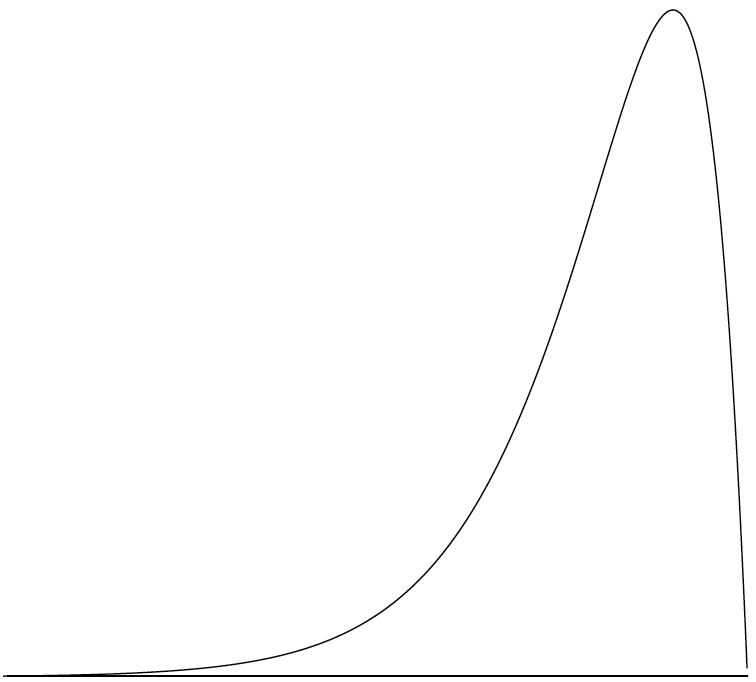
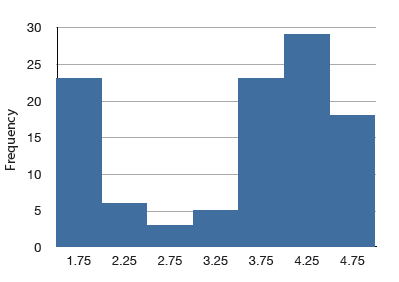
En la Figura se muestra una distribución continua con un sesgo negativo\(\PageIndex{9}\). Las distribuciones mostradas hasta ahora tienen un punto alto o pico distinto. La distribución en la Figura\(\PageIndex{10}\) tiene dos picos distintos. Una distribución con dos picos se denomina distribución bimodal.
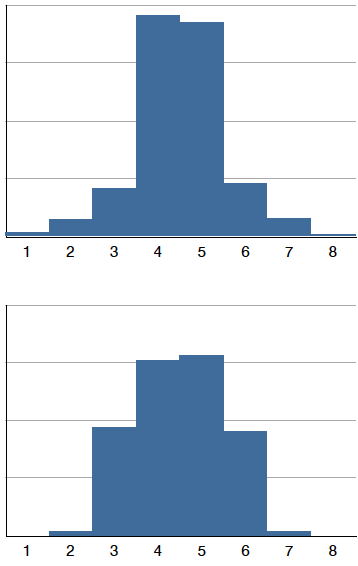
Las distribuciones también difieren entre sí en términos de cuán grandes o “gordas” son sus colas. La figura\(\PageIndex{11}\) muestra dos distribuciones que difieren a este respecto. La distribución superior tiene relativamente más puntajes en sus colas; su forma se llama leptokúrtica. La distribución inferior tiene relativamente menos puntuaciones en sus colas; su forma se llama platykurtic.
Colaboradores y Atribuciones
- Template:Lane
- David M. Lane and Heidi Ziemer


