14.6: Observaciones influyentes
- Page ID
- 152300
Objetivos de aprendizaje
- Describir lo que hace que un punto influya
- Definir “distancia”
Es posible que una sola observación tenga una gran influencia en los resultados de un análisis de regresión. Por lo tanto, es importante estar alerta ante la posibilidad de observaciones influyentes y tomarlas en consideración a la hora de interpretar los resultados.
Influencia
La influencia de una observación puede pensarse en términos de cuánto diferirían los puntajes previstos para otras observaciones si no se incluyera la observación en cuestión. La D de Cook es una buena medida de la influencia de una observación y es proporcional a la suma de las diferencias cuadradas entre las predicciones realizadas con todas las observaciones en el análisis y las predicciones realizadas dejando fuera la observación en cuestión. Si las predicciones son las mismas con o sin la observación en cuestión, entonces la observación no influye en el modelo de regresión. Si las predicciones difieren mucho cuando la observación no está incluida en el análisis, entonces la observación es influyente.
Una regla general común es que una observación con un valor de D de Cook sobre\(1.0\) tiene demasiada influencia. Al igual que con todas las reglas generales, esta regla debe aplicarse juiciosamente y no irreflexivamente.
La influencia de una observación es función de dos factores:
- Cuánto difiere el valor de la observación en la variable predictora de la media de la variable predictora y
- La diferencia entre la puntuación predicha para la observación y su puntaje real.
El primer factor se llama apalancamiento de la observación. Este último factor se denomina distancia de observación.
Cálculo de Cook D (Opcional)
El primer paso para calcular el valor de D de Cook para una observación es predecir todas las puntuaciones en los datos una vez usando una ecuación de regresión basada en todas las observaciones y una vez usando todas las observaciones excepto la observación en cuestión. El segundo paso es calcular la suma de las diferencias cuadradas entre estos dos conjuntos de predicciones. El paso final es dividir este resultado por\(2\) veces el\(MSE\) (ver la sección sobre particionar la varianza).
Apalancamiento
El apalancamiento de una observación se basa en cuánto difiere el valor de la observación en la variable predictora de la media de la variable predictora. Cuanto mayor sea el apalancamiento de una observación, más potencial tiene para ser una observación influyente. Por ejemplo, una observación con un valor igual a la media en la variable predictora no influye en la pendiente de la línea de regresión independientemente de su valor en la variable criterio. Por otro lado, una observación extrema sobre la variable predictora tiene el potencial de afectar mucho la pendiente.
Cálculo de Apalancamiento (h)
El primer paso es estandarizar la variable predictora para que tenga una media de\(0\) y una desviación estándar de\(1\). Luego, el apalancamiento (\(h\)) se calcula al cuadrado del valor de la observación en la variable predictora estandarizada\(1\), sumando y dividiendo por el número de observaciones.
Distancia
La distancia de una observación se basa en el error de predicción para la observación: Cuanto mayor sea el error de predicción, mayor será la distancia. La medida de distancia más utilizada es la\(\textit{studentized residual}\). El\(\textit{studentized residual}\) para una observación está estrechamente relacionado con el error de predicción para esa observación dividido por la desviación estándar de los errores de predicción. Sin embargo, la puntuación predicha se deriva de una ecuación de regresión en la que no se cuenta la observación en cuestión. Los detalles del cómputo de a\(\textit{studentized residual}\) son un poco complejos y están fuera del alcance de este trabajo.
Incluso una observación con una gran distancia no tendrá tanta influencia si su apalancamiento es bajo. Es la combinación del apalancamiento de una observación y distancia lo que determina su influencia.
Ejemplo\(\PageIndex{1}\)
\(\PageIndex{1}\)La tabla muestra el apalancamiento\(\textit{studentized residual}\), y la influencia para cada una de las cinco observaciones en un pequeño conjunto de datos.
Tabla \(\PageIndex{1}\): Datos de ejemplo
| ID | X | Y | h | R | D |
|---|---|---|---|---|---|
| A | 1 | 2 | 0.39 | -1.02 | 0.40 |
| B | 2 | 3 | 0.27 | -0.56 | 0.06 |
| C | 3 | 5 | 0.21 | 0.89 | 0.11 |
| D | 4 | 6 | 0.20 | 1.22 | 0.19 |
| E | 8 | 7 | 0.73 | -1.68 | 8.86 |
En la tabla anterior,\(h\) is the leverage, \(R\) is the \(\textit{studentized residual}\), y\(D\) is Cook's measure of influence.
\(\text{Observation A}\)tiene un apalancamiento bastante alto, un residual relativamente alto y una influencia moderadamente alta.
\(\text{Observation B}\)tiene un apalancamiento pequeño y un residual relativamente pequeño. Tiene muy poca influencia.
\(\text{Observation C}\)tiene un pequeño apalancamiento y un residual relativamente alto. La influencia es relativamente baja.
\(\text{Observation D}\)tiene el apalancamiento más bajo y el segundo residuo más alto. Si bien su residual es mucho mayor que\(\text{Observation A }\), su influencia es mucho menor debido a su bajo apalancamiento.
\(\text{Observation E}\)tiene, con mucho, el mayor apalancamiento y el mayor residuo. Esta combinación de alto apalancamiento y alto residuo hace que esta observación sea extremadamente influyente.
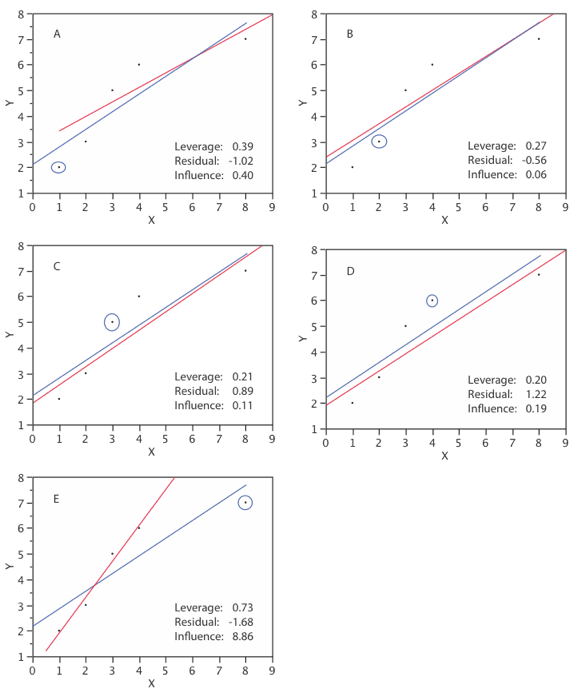
La figura\(\PageIndex{1}\) muestra la línea de regresión para todo el conjunto de datos (azul) y la línea de regresión si no se incluye la observación en cuestión (rojo) para todas las observaciones. La observación en cuestión está enmarcada en un círculo. Naturalmente, la línea de regresión para todo el conjunto de datos es la misma en todos los paneles. El residuo se calcula en relación con la línea para la cual no se incluye en el análisis la observación en cuestión. La observación más influyente es\(\text{Observation E}\) para la cual las dos líneas de regresión son muy diferentes. Esto indica la influencia de esta observación.
