8.1: Los elementos de las pruebas de hipótesis
- Page ID
- 151148
Objetivos de aprendizaje
- Comprender el marco lógico de las pruebas de hipótesis.
- Aprender terminología básica relacionada con las pruebas de hipótesis.
- Conocer hechos fundamentales sobre las pruebas de hipótesis.
Tipos de Hipótesis
Una hipótesis sobre el valor de un parámetro de población es una afirmación sobre su valor. Al igual que en el ejemplo introductorio nos ocuparemos de probar la verdad de dos hipótesis en competencia, de las cuales sólo una puede ser cierta.
Definición: hipótesis nula e hipótesis alternativa
- La hipótesis nula, denotada\(H_0\), es la afirmación sobre el parámetro poblacional que se supone que es verdadera a menos que haya pruebas convincentes de lo contrario.
- La hipótesis alternativa, denotada\(H_a\), es una afirmación sobre el parámetro poblacional que es contradictoria con la hipótesis nula, y se acepta como cierta sólo si hay evidencia convincente a favor de la misma.
Definición: procedimiento estadístico
La prueba de hipótesis es un procedimiento estadístico en el que se elige entre una hipótesis nula y una hipótesis alternativa basada en la información de una muestra.
El resultado final de un procedimiento de prueba de hipótesis es la elección de una de las dos conclusiones posibles siguientes:
- Rechazar\(H_0\) (y por lo tanto aceptar\(H_a\)), o
- No rechazar\(H_0\) (y por lo tanto no aceptar\(H_a\)).
La hipótesis nula representa típicamente el status quo, o lo que históricamente ha sido cierto. En el ejemplo de los respiradores, creeríamos el reclamo del fabricante a menos que haya razón para no hacerlo, por lo que las hipótesis nulas lo son\(H_0:\mu =75\). La hipótesis alternativa en el ejemplo es la afirmación contradictoria\(H_a:\mu <75\). La hipótesis nula siempre será una aserción que contenga un signo igual, pero dependiendo de la situación la hipótesis alternativa puede tener cualquiera de tres formas: con el símbolo\(<\), como en el ejemplo que se acaba de discutir, con el símbolo\(>\), o con el símbolo\(\neq\). Los dos ejemplos siguientes ilustran los dos últimos casos.
Ejemplo\(\PageIndex{1}\)
Un editor de libros de texto universitarios afirma que el precio promedio de todos los libros de texto universitarios de encuadernación dura es\(\$127.50\). Un grupo de estudiantes cree que la media real es mayor y desea poner a prueba su creencia. Declarar las hipótesis nulas y alternativas pertinentes.
Solución:
La opción predeterminada es aceptar la afirmación del editor a menos que haya pruebas convincentes de lo contrario. Así es la hipótesis nula\(H_0:\mu =127.50\). Dado que el grupo de estudiantes piensa que el precio promedio del libro de texto es mayor que la cifra del editor, la hipótesis alternativa en esta situación es\(H_a:\mu >127.50\).
Ejemplo\(\PageIndex{2}\)
La receta de un artículo de panadería está diseñada para dar como resultado un producto que contiene\(8\) gramos de grasa por porción. El departamento de control de calidad muestrea el producto periódicamente para asegurar que el proceso de producción esté funcionando según lo diseñado. Declarar las hipótesis nulas y alternativas pertinentes.
Solución:
La opción por defecto es asumir que el producto contiene la cantidad de grasa que fue formulado para contener a menos que haya evidencia convincente de lo contrario. Así es la hipótesis nula\(H_0:\mu =8.0\). Dado que contener ya sea más grasa de la deseada o contener menos grasa de la deseada son ambos una indicación de un proceso de producción defectuoso, la hipótesis alternativa en esta situación es que la media es diferente de\(8.0\), entonces\(H_a:\mu \neq 8.0\).
En Ejemplo\(\PageIndex{1}\), el ejemplo del libro de texto, podría parecer más natural que la afirmación del editor sea que el precio promedio es como máximo\(\$127.50\), no exactamente\(\$127.50\). Si la afirmación se hiciera de esta manera, entonces la hipótesis nula sería\(H_0:\mu \leq 127.50\), y el valor\(\$127.50\) dado en el ejemplo sería el que menos favorable a la afirmación del editor, la hipótesis nula. Siempre es cierto que si la hipótesis nula se conserva por su valor menos favorable, entonces se retiene para cualquier otro valor.
Así, para que las hipótesis nulas y alternativas sean fáciles de distinguir para el alumno, en cada ejemplo y problema de este texto siempre presentaremos una de las dos afirmaciones en competencia sobre el valor de un parámetro con una igualdad. El reclamo expresado con una igualdad es la hipótesis nula. Esto es lo mismo que siempre afirmar la hipótesis nula bajo la luz menos favorable. Entonces, en el ejemplo introductorio sobre los respiradores, afirmamos la afirmación del fabricante como “el promedio son\(75\) minutos” en lugar del quizás más natural “el promedio es al menos\(75\) minutos”, reduciendo esencialmente la presentación de la hipótesis nula a su peor de los casos.
El primer paso en la prueba de hipótesis es identificar las hipótesis nulas y alternativas.
La lógica de las pruebas de hipótesis
Si bien estudiaremos las pruebas de hipótesis en situaciones distintas a las de una sola media poblacional (por ejemplo, para una proporción poblacional en lugar de una media o en la comparación de las medias de dos poblaciones diferentes), en esta sección la discusión siempre se dará en términos de una sola media poblacional\(\mu\).
La hipótesis nula siempre tiene la forma\(H_0:\mu =\mu _0\) para un número específico\(\mu _0\) (en el ejemplo del respirador\(\mu _0=75\), en el ejemplo del libro de texto\(\mu _0=127.50\), y en el ejemplo de los productos horneados\(\mu _0=8.0\)). Dado que la hipótesis nula es aceptada a menos que haya pruebas contundentes de lo contrario, el procedimiento de prueba se basa en la suposición inicial que\(H_0\) es verdadera. Este punto es tan importante que lo repetiremos en una pantalla:
El procedimiento de prueba se basa en la suposición inicial que\(H_0\) es verdadera.
El criterio para juzgar entre\(H_0\) y con\(H_a\) base en los datos de la muestra es: si el valor de\(\overline{X}\) sería muy poco probable que\(H_0\) ocurriera si fuera cierto, pero favorece la verdad de\(H_a\), entonces\(H_0\) rechazamos a favor de\(H_a\). De lo contrario no rechazamos\(H_0\).
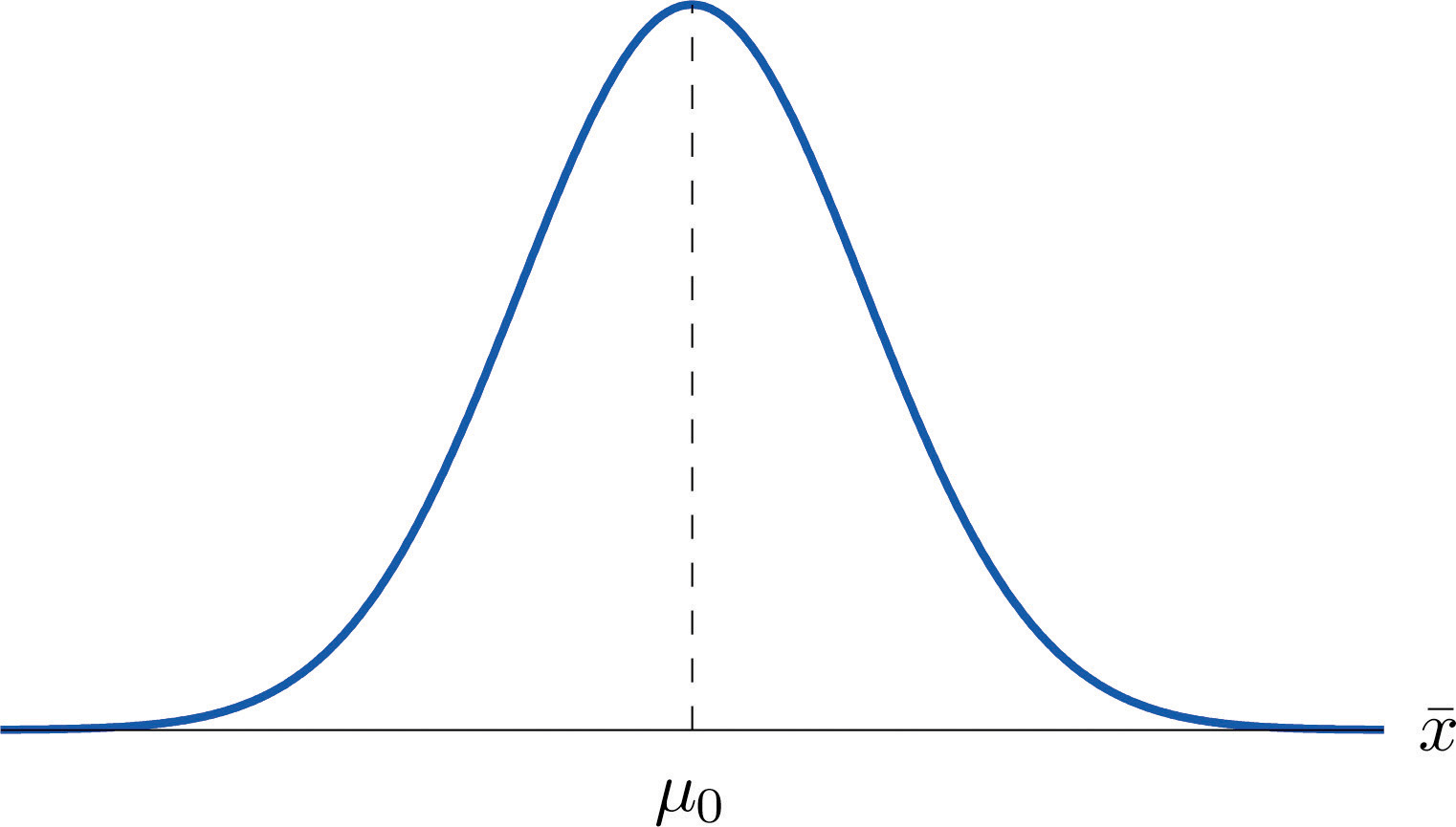
Suponiendo por ahora que\(\overline{X}\) sigue una distribución normal, cuando la hipótesis nula es verdadera la función de densidad para la media muestral\(\overline{X}\) debe ser como en la Figura\(\PageIndex{1}\): una curva de campana centrada en\(\mu _0\). Por lo tanto, si\(H_0\)\(\overline{X}\) es cierto entonces es probable que tome un valor cercano\(\mu _0\) y es poco probable que lleve valores lejos. Por lo tanto, nuestro procedimiento de decisión se reduce simplemente a:
- si\(H_a\) tiene la forma\(H_a:\mu <\mu _0\) entonces rechazar\(H_0\) si\(\bar{x}\) está lejos a la izquierda de\(\mu _0\);
- si\(H_a\) tiene la forma\(H_a:\mu >\mu _0\) entonces rechazar\(H_0\) si\(\bar{x}\) está lejos a la derecha de\(\mu _0\);
- si\(H_a\) tiene la forma\(H_a:\mu \neq \mu _0\) entonces rechazar\(H_0\) si\(\bar{x}\) está lejos de\(\mu _0\) en cualquier dirección.
Piense en el ejemplo del respirador, para el que la hipótesis nula es\(H_0:\mu =75\), la afirmación de que el tiempo promedio que se entrega aire para todos los respiradores es de\(75\) minutos. Si la media de la muestra es\(75\) o mayor entonces ciertamente no rechazaríamos\(H_0\) (ya que no hay problema con que un respirador de emergencia entregue aire incluso más largo de lo reclamado).
Si la media de la muestra es ligeramente menor que\(75\) entonces lógicamente atribuiríamos la diferencia al error de muestreo y\(H_0\) tampoco rechazaríamos.
Los valores de la media muestral que son cada vez más pequeños tienen cada vez menos probabilidades de provenir de una población para la que la media poblacional es\(75\). Así, si la media muestral es mucho menor que\(75\), digamos alrededor de\(60\) minutos o menos, entonces sin duda rechazaríamos\(H_0\), porque sabemos que es muy poco probable que el promedio de una muestra sea tan bajo si la media poblacional fuera\(75\). Este es el criterio de evento raro para el rechazo: lo que realmente observamos\((\overline{X}<60)\) sería un evento tan raro si\(\mu =75\) fuera cierto que lo consideramos mucho más probable que la hipótesis alternativa\(\mu <75\) sostenga.
En resumen, para decidir entre\(H_0\) y\(H_a\) en este ejemplo seleccionaríamos una “región de rechazo” de valores suficientemente alejados a la izquierda de\(75\), basados en el criterio de eventos raros, y rechazaríamos\(H_0\) si la media de la muestra\(\overline{X}\) se encuentra en la región de rechazo, pero no rechazaríamos\(H_0\) si no lo hace.
La Región del Rechazo
Cada forma diferente de la hipótesis alternativa Ha tiene su propio tipo de región de rechazo:
- si (como en el ejemplo del respirador)\(H_a\) tiene la forma\(H_a:\mu <\mu _0\), rechazamos\(H_0\) si\(\bar{x}\) está lejos a la izquierda de\(\mu _0\), es decir, a la izquierda de algún número\(C\), por lo que la región de rechazo tiene la forma de un intervalo\((-\infty ,C]\);
- si (como en el ejemplo del libro de texto)\(H_a\) tiene la forma\(H_a:\mu >\mu _0\), rechazamos\(H_0\) si\(\bar{x}\) está lejos a la derecha de\(\mu _0\), es decir, a la derecha de algún número\(C\), por lo que la región de rechazo tiene la forma de un intervalo\([C,\infty )\);
- si (como en el buen ejemplo horneado)\(H_a\) tiene la forma\(H_a:\mu \neq \mu _0\), rechazamos\(H_0\) si\(\bar{x}\) está lejos de\(\mu _0\) en cualquier dirección, es decir, ya sea a la izquierda de algún número\(C\) o a la derecha de algún otro número\(C′\), por lo que la región de rechazo tiene la forma de la unión de dos intervalos\((-\infty ,C]\cup [C',\infty )\).
El tema clave en nuestra línea de razonamiento es la cuestión de cómo determinar el número\(C\) o números\(C\) y\(C′\), denominado el valor crítico o valores críticos de la estadística, que determinan la región de rechazo.
Definición: valores críticos
El valor crítico o valores críticos de una prueba de hipótesis son el número o números que determinan la región de rechazo.
Supongamos que la región de rechazo es un solo intervalo, por lo que necesitamos seleccionar un solo número\(C\). Aquí está el procedimiento para hacerlo. Seleccionamos una pequeña probabilidad, denotada\(\alpha\), digamos\(1\%\), que tomamos como nuestra definición de “evento raro”: un evento es “raro” si su probabilidad de ocurrencia es menor que\(\alpha\). (En todos los ejemplos y problemas de este texto ya se\(\alpha\) dará el valor de.) La probabilidad de que\(\overline{X}\) tome un valor en un intervalo es el área bajo su curva de densidad y por encima de ese intervalo, así como se muestra en la Figura\(\PageIndex{2}\) (dibujado bajo el supuesto de que\(H_0\) es cierto, de modo que la curva se centra en\(\mu _0\)) el valor crítico\(C\) es el valor de\(\overline{X}\) que corta un área de cola\(\alpha\) en la curva de densidad de probabilidad de\(\overline{X}\). Cuando la región de rechazo está en dos piezas, es decir, compuesta por dos intervalos, el área total por encima de ambas debe ser\(\alpha\), por lo que el área por encima de cada una está\(\alpha /2\), como también se muestra en la Figura\(\PageIndex{2}\).
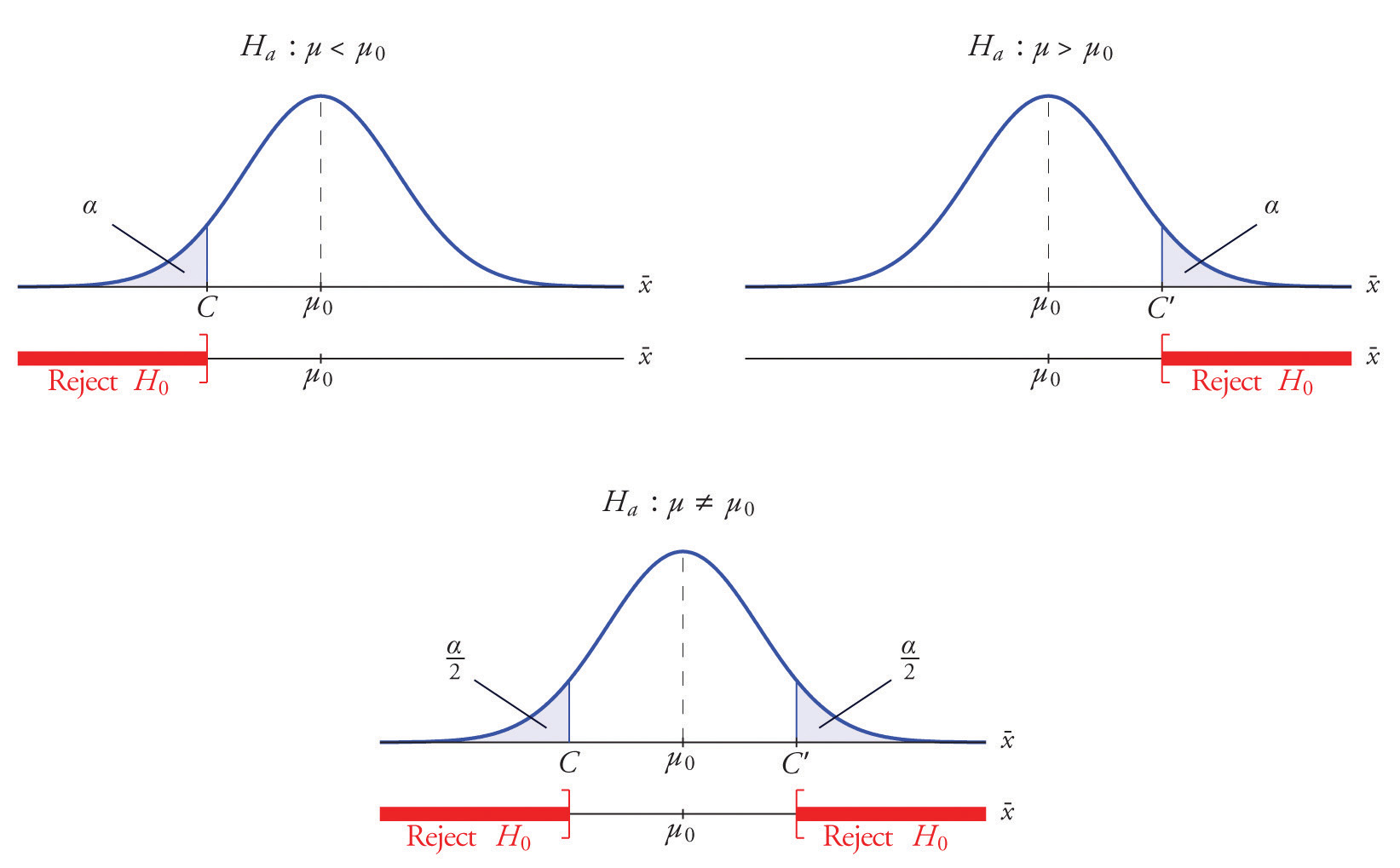
El número\(\alpha\) es el área total de una cola o un par de colas.
Ejemplo\(\PageIndex{3}\)
En el contexto de Ejemplo\(\PageIndex{2}\), supongamos que se sabe que la población se distribuye normalmente con desviación estándar\(\alpha =0.15\) gram, y supongamos que la prueba de hipótesis\(H_0:\mu =8.0\) versus se\(H_a:\mu \neq 8.0\) realizará con una muestra de tamaño\(5\). Construir la región de rechazo para la prueba para la elección\(\alpha =0.10\). Explicar el procedimiento de decisión e interpretarlo.
Solución:
Si\(H_0\) es cierto entonces la media de la muestra\(\overline{X}\) se distribuye normalmente con la media y la desviación estándar
\[\begin{align} \mu _{\overline{X}} &=\mu \nonumber \\[5pt] &=8.0 \nonumber \end{align} \nonumber\]
\[\begin{align} \sigma _{\overline{X}}&=\dfrac{\sigma}{\sqrt{n}} \nonumber \\[5pt] &= \dfrac{0.15}{\sqrt{5}} \nonumber\\[5pt] &=0.067 \nonumber \end{align} \nonumber\]
Dado que\(H_a\) contiene el\(\neq\) símbolo la región de rechazo estará en dos piezas, cada una correspondiente a una cola de área\(\alpha /2=0.10/2=0.05\). De la Figura 7.1.6\(z_{0.05}=1.645\), así\(C\) y\(C′\) son desviaciones\(1.645\) estándar de\(\overline{X}\) a la derecha e izquierda de su media\(8.0\):
\[C=8.0-(1.645)(0.067) = 7.89 \; \; \text{and}\; \; C'=8.0 + (1.645)(0.067) = 8.11\]
El resultado se muestra en la Figura\(\PageIndex{3}\). α = 0.1
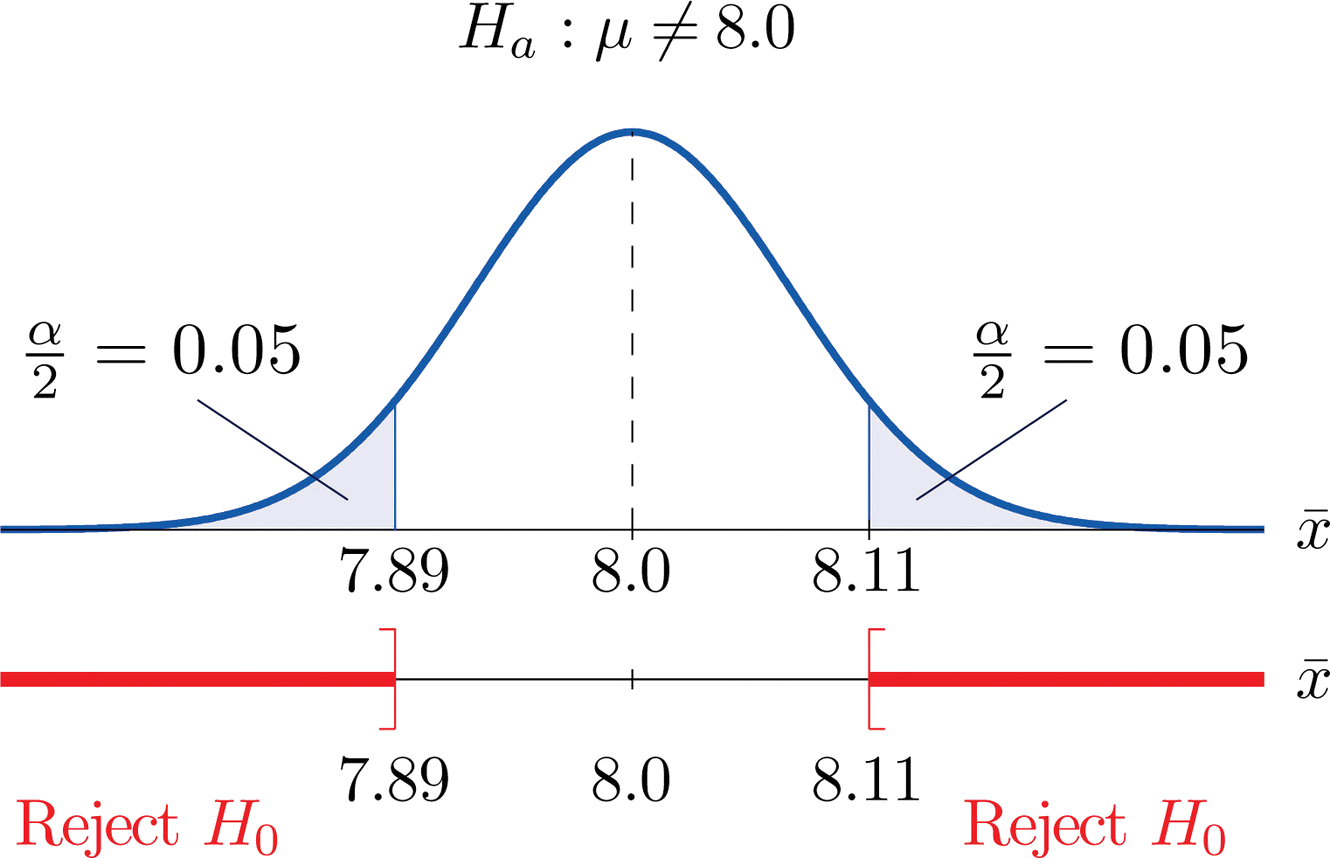
El procedimiento de decisión es: tomar una muestra de tamaño\(5\) y calcular la media de la muestra\(\bar{x}\). Si\(\bar{x}\) es\(7.89\) gramos o menos o\(8.11\) gramos o más entonces rechazar la hipótesis de que la cantidad promedio de grasa en todas las porciones del producto es\(8.0\) gramos a favor de la alternativa de que es diferente a los\(8.0\) gramos. De lo contrario no rechace la hipótesis de que la cantidad promedio es de\(8.0\) gramos.
El razonamiento es que si la verdadera cantidad promedio de grasa por porción fueran\(8.0\) gramos entonces habría menos de una\(10\%\) posibilidad de que una muestra de tamaño\(5\) produjera una media de\(7.89\) gramos o menos o\(8.11\) gramos o más. De ahí que si eso sucediera sería más probable que el valor\(8.0\) sea incorrecto (siempre asumiendo que la desviación estándar de la población es\(0.15\) gramo).
Debido a que las regiones de rechazo se calculan en base a áreas en colas de distribuciones, como se muestra en la Figura\(\PageIndex{2}\), las pruebas de hipótesis se clasifican de acuerdo con la forma de la hipótesis alternativa de la siguiente manera.
Definiciones: Clasificaciones de prueba
- Si\(H_a\) tiene la forma\(\mu \neq \mu _0\) la prueba se llama prueba de dos colas.
- Si\(H_a\) tiene la forma\(\mu < \mu _0\) la prueba se llama prueba de cola izquierda.
- Si\(H_a\) tiene la forma\(\mu > \mu _0\) la prueba se llama prueba de cola derecha.
Cada una de las dos últimas formas también se llama prueba de una cola.
Dos tipos de errores
El formato del procedimiento de prueba en términos generales es tomar una muestra y utilizar la información que contiene para llegar a una decisión sobre las dos hipótesis. Como se dijo antes nuestra decisión siempre será
- rechazar la hipótesis nula\(H_0\) a favor de la alternativa\(H_a\) presentada, o
- no\(H_0\) rechacen la hipótesis nula a favor de la alternativa\(H_0\) presentada.
Hay cuatro posibles resultados del procedimiento de prueba de hipótesis, como se muestra en la siguiente tabla:
| Verdadero Estado de la Naturaleza | |||
|---|---|---|---|
| \(H_0\)es verdad | \(H_0\)es falso | ||
| NUESTRA DECISIÓN | No rechace\(H_0\) | Decisión correcta | Error de tipo II |
| Rechazar\(H_0\) | Error de tipo I | Decisión correcta | |
Como muestra la tabla, hay dos formas de tener razón y dos formas de equivocarse. Normalmente rechazar\(H_0\) cuando en realidad es cierto es un error más grave que no rechazarlo cuando es falso, por lo que el primer error se etiqueta como “Tipo I” y el segundo error “Tipo II”.
Definición: Errores Tipo I y Tipo II
En una prueba de hipótesis:
- Un error de Tipo I es la decisión de rechazar\(H_0\) cuando de hecho es cierto.
- Un error de Tipo II es la decisión de no rechazar\(H_0\) cuando en realidad no es cierto.
A menos que realicemos un censo no tenemos ciertos conocimientos, por lo que no sabemos si nuestra decisión coincide con el verdadero estado de la naturaleza o si hemos cometido un error. Rechazamos\(H_0\) si lo que observamos sería un evento “raro” si\(H_0\) fuera cierto. Pero los eventos raros no son imposibles: ocurren con probabilidad\(\alpha\). Así, cuando\(H_0\) es cierto, se observará un evento raro en la proporción\(\alpha\) de pruebas similares repetidas, y se\(H_0\) rechazará erróneamente en esas pruebas. Así\(\alpha\) es la probabilidad de que al seguir el procedimiento de prueba para decidir entre\(H_0\) y\(H_a\) hagamos un error Tipo I.
Definición: nivel de significación
El número\(\alpha\) que se utiliza para determinar la región de rechazo se denomina nivel de significancia de la prueba. Es la probabilidad de que el procedimiento de prueba resulte en un error Tipo I.
La probabilidad de cometer un error Tipo II es demasiado complicada de discutir en un texto inicial, por lo que no diremos más al respecto que esto: para un tamaño de muestra fijo, elegir\(alpha\) más pequeño para reducir la posibilidad de cometer un error de Tipo I tiene el efecto de aumentar la probabilidad de hacer un Tipo II error. La única manera de reducir simultáneamente las posibilidades de cometer cualquier tipo de error es aumentar el tamaño de la muestra.
Estandarización de la Estadística de Pruebas
Las pruebas de hipótesis se considerarán en varios contextos, y los resultados de gran unificación y simplificación cuando se estandariza el estadístico muestral relevante restándole su media y luego dividiendo por su desviación estándar. El estadístico resultante se denomina estadístico de prueba estandarizado. En cada situación tratada en este y en los dos capítulos siguientes el estadístico de prueba estandarizado tendrá ya sea la distribución normal estándar o la\(t\) distribución de Student.
Definición: prueba de hipótesis
Un estadístico de prueba estandarizado para una prueba de hipótesis es el estadístico que se forma restando del estadístico de interés su media y dividiendo por su desviación estándar.
Por ejemplo, revisando Ejemplo\(\PageIndex{3}\), si en lugar de trabajar con la media de la muestra en su lugar\(\overline{X}\) trabajamos con el estadístico de prueba
\[\frac{\overline{X}-8.0}{0.067}\]
entonces la distribución involucrada es normal estándar y los valores críticos son justos\(\pm z_{0.05}\). El trabajo extra que se hizo para encontrar eso\(C=7.89\) y\(C′=8.11\) se elimina. En cada prueba de hipótesis de este libro el estadístico de prueba estandarizado se regirá ya sea por la distribución normal estándar o por la\(t\) distribución de Student. La información sobre las regiones de rechazo se resume en las siguientes tablas:
| Símbolo en\(H_a\) | Terminología | Región de Rechazo |
|---|---|---|
| \ (H_a\)” style="vertical-align:middle; ">< | Prueba de cola izquierda | \((-\infty ,-z_\alpha ]\) |
| \ (H_a\)” style="vertical-align:middle; ">> | Prueba de cola derecha | \([z_\alpha ,\infty )\) |
| \ (H_a\)” style="vertical-align:middle; ">≠ | Prueba de dos colas | \((-\infty ,-z_{\alpha/2} ]\cup [z_{\alpha /2},\infty )\) |
| Símbolo en\(H_a\) | Terminología | Región de Rechazo |
|---|---|---|
| \ (H_a\)” style="vertical-align:middle; ">< | Prueba de cola izquierda | \((-\infty ,-t_\alpha ]\) |
| \ (H_a\)” style="vertical-align:middle; ">> | Prueba de cola derecha | \([t_\alpha ,\infty )\) |
| \ (H_a\)” style="vertical-align:middle; ">≠ | Prueba de dos colas | \((-\infty ,-t_{\alpha/2} ]\cup [t_{\alpha /2},\infty )\) |
Cada instancia de prueba de hipótesis discutida en este y los dos capítulos siguientes tendrá una región de rechazo como una de las seis formas tabuladas en las tablas anteriores.
No importa cuál sea el contexto, siempre se puede realizar una prueba de hipótesis aplicando el siguiente procedimiento sistemático, que se ilustrará en los ejemplos de las secciones siguientes.
Procedimiento de prueba sistemática de hipótesis: enfoque de valor crítico
- Identificar las hipótesis nulas y alternativas.
- Identificar el estadístico de prueba relevante y su distribución.
- Compute a partir de los datos el valor del estadístico de prueba.
- Construir la región de rechazo.
- Compare el valor calculado en el Paso 3 con la región de rechazo construida en el Paso 4 y tome una decisión. Formular la decisión en el contexto del problema, en su caso.
El procedimiento que hemos esbozado en esta sección se denomina el “Enfoque de Valor Crítico” a las pruebas de hipótesis para distinguirlo de un enfoque alternativo pero equivalente que se introducirá al final de la Sección 8.3.
Llave para llevar
- Una prueba de hipótesis es un proceso estadístico para decidir entre dos aseveraciones competitivas sobre un parámetro poblacional.
- El procedimiento de prueba se formaliza en un procedimiento de cinco pasos.

