8.3: La significancia observada de una prueba
- Page ID
- 151152
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Objetivos de aprendizaje
- Conocer cuál es la significación observada de una prueba.
- Aprender a calcular la significancia observada de una prueba.
- Aprender a aplicar el enfoque\(p\) -value a las pruebas de hipótesis.
La significación observada
La base conceptual de nuestro procedimiento de prueba es que rechazamos\(H_0\) solo si los datos que obtuvimos constituirían un evento raro si realmente\(H_0\) fueran ciertos. El nivel de significancia α especifica lo que se entiende por “raro”. La significancia observada de la prueba es una medida de cuán raro sería el valor del estadístico de prueba que acabamos de observar si la hipótesis nula fuera cierta. Es decir, la significancia observada de la prueba recién realizada es la probabilidad de que, si la prueba se repitiera con una nueva muestra, el resultado de la nueva prueba sería al menos tan contrario\(H_0\) y en apoyo de\(H_a\) como lo observado en la prueba original.
Definición: significación observada
La significancia observada o\(p\) -valor de una prueba específica de hipótesis es la probabilidad, en la suposición que\(H_0\) es verdadera, de obtener un resultado al menos tan contrario\(H_0\) y a favor de\(H_a\) como el resultado realmente observado en los datos de la muestra.
Piense en “Ejemplo 8.2.1", Sección 8.2 referente a la efectividad de un nuevo analgésico. Esta fue una prueba de cola izquierda en la que se encontraba el valor del estadístico de prueba\(-1.886\). Ser tan contrario\(H_0\) y en apoyo de\(H_a\) como el resultado\(Z=-1.886\) realmente observado significa obtener un valor del estadístico de prueba en el intervalo\((-\infty ,-1.886]\). Redondeando\(-1.886\) a\(-1.89\), podemos leer directamente de la Figura 7.1.5 que\(P(Z\leq -1.89)=0.0294\). Así el\(p\) -valor o significancia observada de la prueba en “Ejemplo 8.2.1", Sección 8.2 es\(0.0294\) o aproximadamente\(3\%\). Bajo muestreo repetido de esta población, si\(H_0\) fuera cierto entonces solo aproximadamente\(3\%\) de todas las muestras de tamaño\(50\) darían un resultado como contrario\(H_0\) y a favor de\(H_a\) como la muestra que observamos. Tenga en cuenta que la probabilidad\(0.0294\) es el área de la cola izquierda cortada por el estadístico de prueba en esta prueba de cola izquierda.
El razonamiento análogo se aplica a una prueba de cola derecha o de dos colas, excepto que en el caso de que una prueba de dos colas esté\(0\) tan lejos como el valor observado del estadístico de prueba pero en el lado opuesto de\(0\) es igual de contrario a\(H_0\) que estar a la misma distancia y en el mismo lado de\(0\), de ahí que se duplique el área de cola correspondiente.
Definición computacional de la significancia observada de una prueba de hipótesis
La significancia observada de una prueba de hipótesis es el área de la cola de la distribución cortada por el estadístico de prueba (veces dos en el caso de una prueba de dos colas).
Ejemplo\(\PageIndex{1}\)
Compute la significancia observada de la prueba realizada en “Ejemplo 8.2.2", Sección 8.2.
Solución:
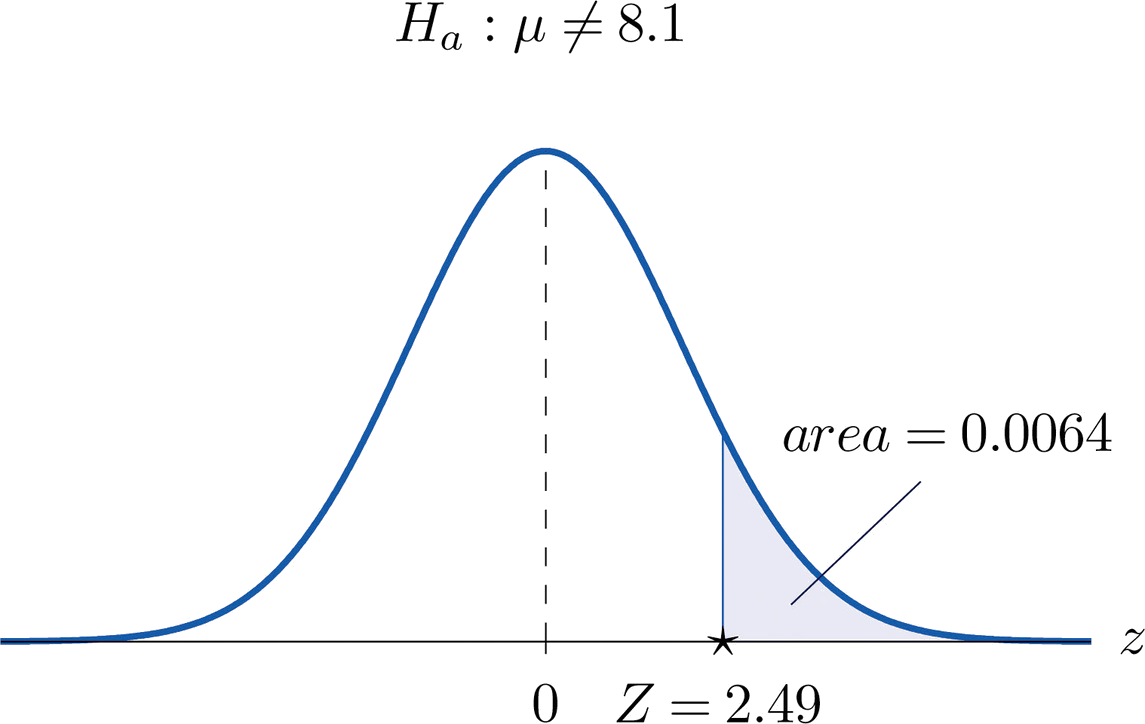
El valor del estadístico de prueba fue\(z=2.490\), que por la Figura 7.1.5 corta una cola de área\(0.0064\), como se muestra en la Figura\(\PageIndex{1}\). Dado que la prueba fue de dos colas, la significación observada es\(2\times 0.0064=0.0128\).
El enfoque del valor p para las pruebas de hipótesis
En “Ejemplo 8.2.1", Sección 8.2 la prueba se realizó a\(5\%\) nivel de significancia: la definición de evento “raro” fue probabilidad\(\alpha =0.05\) o menor. Vimos anteriormente que la significación observada de la prueba era\(p=0.0294\) o aproximadamente\(3\%\). Ya que\(p=0.0294<0.05=\alpha\) (o\(3\%\) es menor que\(5\%\)), la decisión resultó ser rechazar: lo que se observó era suficientemente improbable para calificar como un evento tan raro como para ser considerado como (prácticamente) incompatible con\(H_0\).
En “Ejemplo 8.2.2", Sección 8.2 la prueba se realizó a\(1\%\) nivel de significancia: la definición de evento “raro” fue probabilidad\(\alpha =0.01\) o menor. La significancia observada de la prueba se computó en “Ejemplo\(\PageIndex{1}\)" como\(p=0.0128\) o aproximadamente\(1.3\%\). Ya que\(p=0.0128>0.01=\alpha\) (o\(1.3\%\) es mayor que\(1\%\)), la decisión resultó ser no rechazar. El evento observado fue poco probable, pero no lo suficientemente improbable que condujera al rechazo de la hipótesis nula.
El razonamiento que se acaba de presentar es la base para una formulación ligeramente diferente pero equivalente del proceso de prueba de hipótesis. Los tres primeros pasos son los mismos que antes, pero en lugar de usar\(\alpha\) para calcular valores críticos y construir una región de rechazo, se calcula el\(p\) -valor\(p\) de la prueba y se compara con\(\alpha\), rechazando\(H_0\) si\(p\leq \alpha\) y no rechazando si\(p>\alpha\).
Procedimiento de Prueba Sistemática de Hipótesis: Enfoque de Valor
- Identificar las hipótesis nulas y alternativas.
- Identificar el estadístico de prueba relevante y su distribución.
- Compute a partir de los datos el valor del estadístico de prueba.
- Compute el\(p\) -valor de la prueba.
- Compare el valor calculado en el Paso 4 con el nivel de significancia α y tome una decisión: rechazar\(H_0\) si\(p\leq \alpha\) y no rechazar\(H_0\) si\(p>\alpha\). Formular la decisión en el contexto del problema, en su caso.
Ejemplo\(\PageIndex{2}\)
El puntaje total en un juego de basquetbol profesional es la suma de los puntajes de los dos equipos. Un comentarista experto afirma que el puntaje promedio total para los juegos de la NBA es\(202.5\). Un fan sospecha que esto es una exageración y que el promedio real es menor que\(202.5\). Selecciona una muestra aleatoria de\(85\) juegos y obtiene una puntuación media total de\(199.2\) con desviación estándar\(19.63\). Determinar, a\(5\%\) nivel de significación, si hay pruebas suficientes en la muestra para rechazar la afirmación del comentarista experto.
Solución:
- Paso 1. \(\mu\)Sea el verdadero puntaje promedio total de juego de todos los juegos de la NBA. La prueba relevante es\[H_0: \mu =202.5\\ \text{vs}\\ H_a: \mu <202.5\; @\; \alpha =0.05\]
- Paso 2. La muestra es grande y se desconoce la desviación estándar poblacional. Así, el estadístico de prueba es\[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}\] y tiene la distribución normal estándar.
- Paso 3. Insertar los datos en la fórmula para el estadístico de prueba da\[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}=\frac{199.2-202.5}{19.63/\sqrt{85}}=-1.55\]
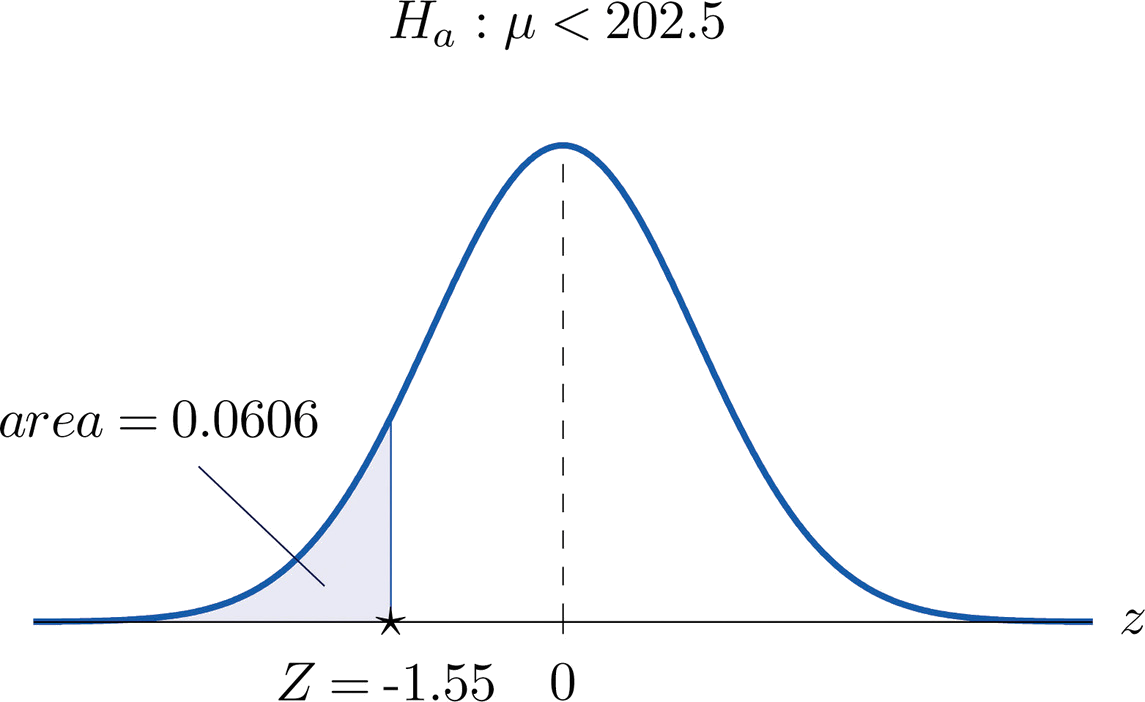
- Paso 4. El área de la cola izquierda cortada por\(z=-1.55\) es, por la Figura 7.1.5,\(0.0606\), como se ilustra en la Figura\(\PageIndex{2}\). Dado que la prueba es de cola izquierda, el\(p\) -valor es solo este número,\(p=0.0606\).
- Paso 5. Ya que\(p=0.0606>0.05=\alpha\), la decisión no es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos no proporcionan evidencia suficiente, a\(5\%\) nivel de significancia, para concluir que el puntaje total promedio de los juegos de la NBA es menor que\(202.5\).
Ejemplo\(\PageIndex{3}\)
El señor Prospero ha estado enseñando Álgebra II de un libro de texto en particular en Remote Isle High School durante muchos años. A lo largo de los años, los alumnos de sus clases de Álgebra II han obtenido consistentemente una media de\(67\) exámenes de fin de curso (EOC). Este año el señor Próspero utilizó un nuevo libro de texto con la esperanza de que el puntaje promedio en la prueba EOC fuera mayor. El puntaje promedio de la prueba EOC de los\(64\) estudiantes que tomaron Álgebra II del Sr. Próspero este año tuvo desviación estándar media\(69.4\) y muestral\(6.1\). Determinar si estos datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que el puntaje promedio de la prueba EOC es mayor con el nuevo libro de texto.
Solución:
- Paso 1. \(\mu\)Sea el verdadero puntaje promedio en el examen EOC de todos los alumnos del señor Próspero que toman el curso Álgebra II con el nuevo libro de texto. La afirmación natural que se asumiría verdadera a menos que hubiera pruebas contundentes de lo contrario es que el nuevo libro es aproximadamente el mismo que el antiguo. La alternativa, que se necesita evidencia para establecer, es que el nuevo libro es mejor, lo que corresponde a un mayor valor de\(\mu\). Por lo tanto, la prueba relevante es\[H_0: \mu =67\\ \text{vs}\\ H_a: \mu >67\; @\; \alpha =0.01\]
- Paso 2. La muestra es grande y se desconoce la desviación estándar poblacional. Así, el estadístico de prueba es\[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}\] y tiene la distribución normal estándar.
- Paso 3. Insertar los datos en la fórmula para el estadístico de prueba da\[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}=\frac{69.4-67}{6.1/\sqrt{64}}=3.15\]
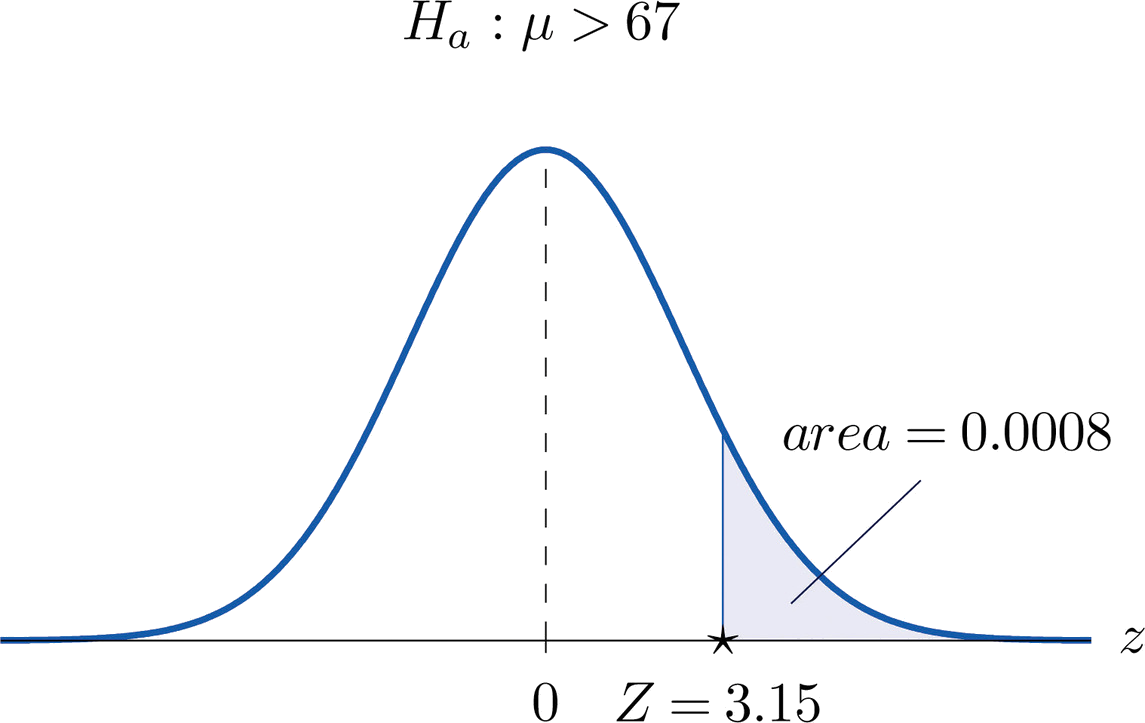
- Paso 4. El área de la cola derecha cortada por\(z=3.15\) es, por la Figura 7.1.5,\(1-0.9992=0.0008\), como se muestra en la Figura\(\PageIndex{3}\). Dado que la prueba es de cola derecha, el\(p\) -valor es solo este número,\(p=0.0008\).
- Paso 5. Ya que\(p=0.0008<0.01=\alpha\), la decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que el puntaje promedio del examen EOC de los estudiantes que cursan el curso de Álgebra II del señor Próspero usando el nuevo libro es mayor que la puntuación promedio de quienes toman el curso de él pero que utilizan el libro antiguo.
Ejemplo\(\PageIndex{4}\)
Para las aguas superficiales en un lago en particular, a los científicos ambientales locales les gustaría mantener un nivel de pH promedio en\(7.4\). Las muestras de agua se recolectan rutinariamente para monitorear el nivel de pH promedio. Si hay evidencia de un cambio en el valor del pH, en cualquier dirección, entonces se tomarán medidas correctivas. En un día particular se toman muestras de\(30\) agua y se obtienen lecturas de pH promedio\(7.7\) con desviación estándar de la muestra\(0.5\). Determinar, a\(1\%\) nivel de significancia, si hay evidencia suficiente en la muestra para indicar que se deben tomar medidas correctivas.
Solución:
- Paso 1. \(\mu\)Sea el verdadero nivel de pH promedio en el momento en que se tomaron las muestras. La prueba relevante es\[H_0: \mu =7.4\\ \text{vs}\\ H_a: \mu \neq 7.4\; @\; \alpha =0.01\]
- Paso 2. La muestra es grande y se desconoce la desviación estándar poblacional. Así, el estadístico de prueba es\[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}\] y tiene la distribución normal estándar.
- Paso 3. Insertar los datos en la fórmula para el estadístico de prueba da\[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}=\frac{7.7-7.4}{0.5/\sqrt{30}}=3.29\]
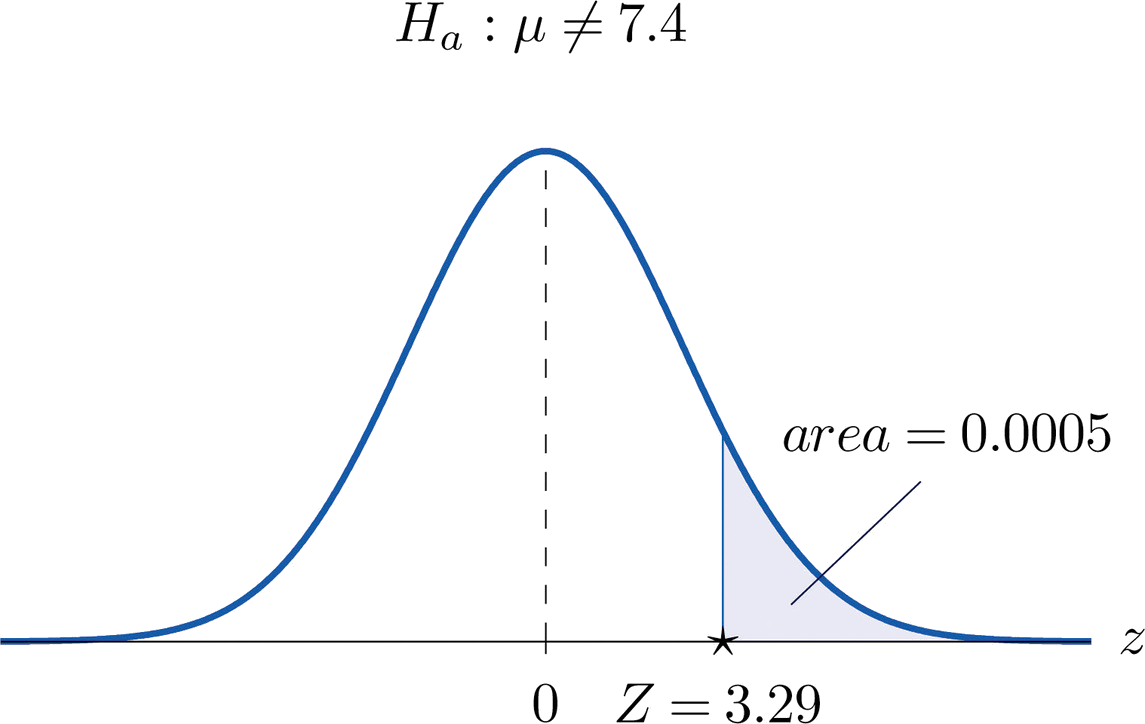
- Paso 4. El área de la cola derecha cortada por\(z=3.29\) es, por la Figura 7.1.5,\(1-0.9995=0.0005\), como se ilustra en la Figura\(\PageIndex{4}\). Dado que la prueba es de dos colas, el valor p es el doble de este número, p=2×0.0005=0.0010.
- Paso 5. Ya que\(p=0.0010<0.01=\alpha\), la decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que el pH promedio de las aguas superficiales en el lago es diferente de\(7.4\). Es decir, se indica la acción correctiva.
Llave para llevar
- La significancia observada o\(p\) -valor de una prueba es una medida de cuán inconsistente es el resultado de la muestra con\(H_0\) y a favor de\(H_a\).
- El enfoque\(p\) -value para la prueba de hipótesis significa que uno simplemente compara el\(p\) -valor\(\alpha\) en lugar de construir una región de rechazo.
- Existe un procedimiento sistemático de cinco pasos para el enfoque\(p\) -value para la prueba de hipótesis.

