3.4: Análisis Residual

La función summary () proporciona una cantidad sustancial de información para ayudarnos a evaluar el ajuste de un modelo de regresión a los datos utilizados para desarrollar ese modelo. Para profundizar en la calidad del modelo, podemos analizar información adicional sobre los valores observados en comparación con los valores que predice el modelo. En particular, el análisis residual examina estos valores residuales para ver qué nos pueden decir sobre la calidad del modelo.

Recordemos que el valor residual es la diferencia entre el valor medido real almacenado en el marco de datos y el valor que predice la línea de regresión ajustada para ese punto de datos correspondiente. Los valores residuales mayores a cero significan que el modelo de regresión predijo un valor que era demasiado pequeño en comparación con el valor medido real, y los valores negativos indican que el modelo de regresión predijo un valor que era demasiado grande. Un modelo que se ajuste bien a los datos tendería a sobrepredecir tantas veces como subpredice. Así, si trazamos los valores residuales, esperaríamos verlos distribuidos uniformemente alrededor de cero para un modelo bien ajustado.

Las siguientes llamadas a funciones producen la gráfica de residuos para nuestro modelo, que se muestra en la Figura 3.3.

> plot(fitted(int00.lm),resid(int00.lm))

Figura 3.3: Los valores residuales versus los valores de entrada para el modelo de un factor desarrollado con los datos Int2000.

En esta parcela, vemos que los residuos tienden a aumentar a medida que nos movemos hacia la derecha. Adicionalmente, los residuos no están uniformemente dispersos por encima y por debajo de cero. En general, esta gráfica nos dice que usar el reloj como único predictor en el modelo de regresión no explica suficiente o completamente los datos. En general, si observas algún tipo de tendencia o patrón claro en los residuales, probablemente necesites generar un mejor modelo. Esto no quiere decir que nuestro sencillo modelo de un factor sea inútil, sin embargo. Solo significa que podemos construir un modelo que produzca valores residuales más ajustados y mejores predicciones.

Otra prueba de los residuos utiliza la gráfica cuantile-versus-quantile, o Q-Q. Anteriormente dijimos que, si el modelo se ajusta bien a los datos, esperaríamos que los residuos se distribuyeran normalmente (gaussianos) alrededor de una media de cero. La gráfica Q-Q proporciona una buena indicación visual de si los residuos del modelo están distribuidos normalmente. Las siguientes llamadas a funciones generan la gráfica Q-Q que se muestra en la Figura 3.4:

> qqnorm(resid(int00.lm))
> qqline(resid(int00.lm))

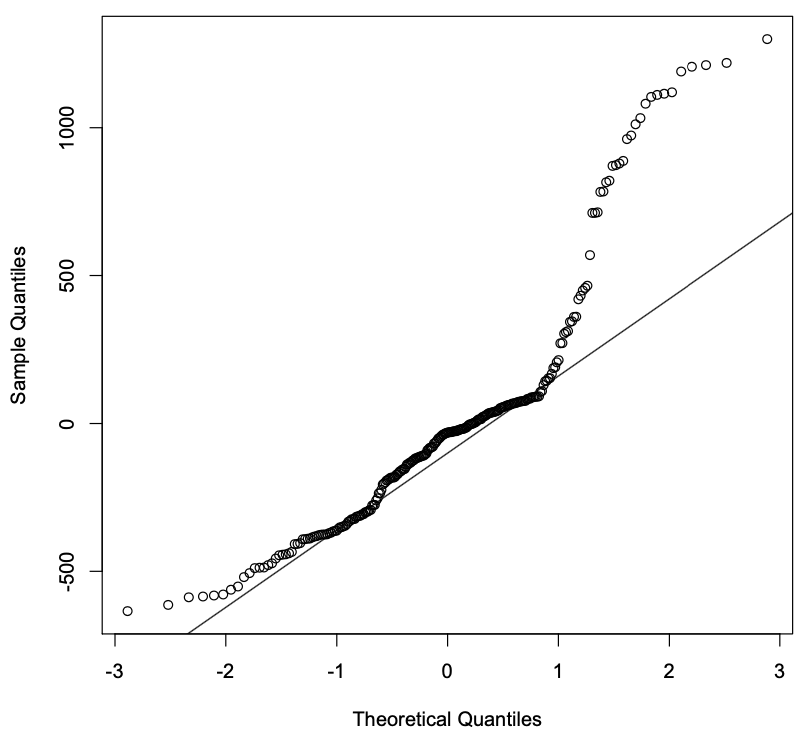
Figura 3.4: La gráfica Q-Q para el modelo de un factor desarrollado con los datos Int2000.

Si los residuos se distribuyeran normalmente, esperaríamos que los puntos trazados en esta figura siguieran una línea recta. Con nuestro modelo, sin embargo, vemos que los dos extremos divergen significativamente de esa línea. Este comportamiento indica que los residuos no se distribuyen normalmente. De hecho, esta trama sugiere que las colas de la distribución son “más pesadas” de lo que esperaríamos de una distribución normal. Esta prueba confirma además que usar solo el reloj como predictor en el modelo es insuficiente para explicar los datos.

Nuestro siguiente paso es aprender a desarrollar modelos de regresión con múltiples factores de entrada. Quizás encontraremos un modelo más complejo que sea mejor capaz de explicar los datos.