Introducción a la Probabilidad
- Última actualización
- 31 oct 2022
- Guardar como PDF
- Page ID
- 151230
( \newcommand{\kernel}{\mathrm{null}\,}\)
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Video
Video: Introducción a la probabilidad (7:41)
Ahora que entendemos cómo la probabilidad encaja en el Big Picture como un elemento clave detrás de la inferencia estadística, estamos listos para aprender más al respecto. Nuestro primer objetivo es introducir alguna terminología fundamental (el lenguaje) y notación que se utiliza al discutir la probabilidad.
La probabilidad no siempre es intuitiva
Aunque la mayoría de los cálculos de probabilidad que realizaremos serán bastante intuitivos debido a su simplicidad, comenzamos con dos ejemplos divertidos que ilustrarán la naturaleza interesante y a veces compleja de la probabilidad.
A menudo, confiar únicamente en nuestra intuición no es suficiente para determinar la probabilidad, por lo que necesitaremos algunas herramientas con las que trabajar, que es exactamente lo que estudiaremos en esta sección.
Precaución
Para los dos siguientes ejemplos, no se preocupen por la solución del problema. Sólo cómo las respuestas a las preguntas de probabilidad no siempre son fáciles de creer o determinar.
Aquí está el primero de dos ejemplos motivadores:
EJEMPLO: La paradoja de “Hagamos un trato”
“Let's Make a Deal” era el nombre de un popular programa de juegos de televisión, que se emitió por primera vez en la década de 1960. La paradoja de “Hagamos un trato” lleva el nombre de ese programa. En el show, el concursante tuvo que elegir entre tres puertas. Una de las puertas tenía un gran premio detrás como un auto o mucho dinero en efectivo, y las otras dos estaban vacías. (En realidad, por el bien del entretenimiento, cada una de las otras dos puertas tenía algún regalo estúpido detrás de ella, como una cabra o un pollo, pero aquí nos referiremos a ellas como vacías).
El concursante tuvo que elegir una de las tres puertas, pero en lugar de revelar la puerta elegida, el anfitrión reveló que una de las dos puertas no elegidas estaba vacía. En este punto del juego, había dos puertas sin abrir (una de las cuales tenía el premio detrás) —la puerta que originalmente había elegido el concursante y la puerta que quedaba sin elegir.
Al concursante se le dio la opción de quedarse con la puerta que inicialmente había elegido, o cambiar a la otra puerta.
¿Qué crees que debería hacer el concursante, quedarse o cambiarse? ¿Cuál crees que es la probabilidad de que ganes el gran premio si te quedas? ¿Y si cambias?
Para que puedas tener una idea de este juego, puedes jugarlo varias veces usando un applet.
Applet interactivo: Hagamos un trato
Ahora bien, ¿qué crees que debería hacer un concursante?
Aprende haciendo: Hagamos un trato
La intuición de la mayoría de la gente es que la posibilidad de ganar es igual ya sea que nos quedemos o cambiemos —que hay una probabilidad 50-50 de ganar con cualquiera de las dos selecciones. Esto, sin embargo, no es el caso.
En realidad, hay un 67% de probabilidad —o una probabilidad de 2/3 (2 de tres )— de ganar cambiando, y solo un 33% de probabilidad —o una probabilidad de 1/3 (1 de 3 )— de ganar al quedarse con la puerta que originalmente se eligió.
Esto significa que un concursante tiene el doble de probabilidades de ganar si cambia a la puerta no elegida. ¿No es esto un poco contradictorio y confuso? La mayoría de la gente piensa así, cuando se enfrentan por primera vez a este problema.
Ahora intentaremos explicarte esta paradoja de dos maneras diferentes:
Video: Hagamos un trato (Explicación #1) (1:10)
Si aún no estás convencido (o incluso si lo estás), aquí tienes una forma diferente de explicar la paradoja:
Video: Hagamos un trato (Explicación #2) (1:37)
Si este ejemplo aún no te persuadió de que la probabilidad no siempre es intuitiva, el siguiente ejemplo definitivamente debería hacer el truco.
EJEMPLO: El problema del cumpleaños
Supongamos que estás en una fiesta con otras 59 personas (para un total de 60). ¿Cuáles son las posibilidades (o, cuál es la probabilidad) de que al menos 2 de los 60 invitados compartan el mismo cumpleaños?
Para aclarar, por “compartir el mismo cumpleaños”, nos referimos a que 2 personas nacieron en la misma fecha, no necesariamente en el mismo año. También, en aras de la simplicidad, ignorar los años bisiestos, y asumir que hay 365 días en cada año.
Aprende haciendo: Problema de cumpleaños
En efecto, existe un 99.4% de probabilidad de que al menos 2 de los 60 invitados compartan el mismo cumpleaños. En otras palabras, es casi seguro que al menos 2 de los invitados comparten el mismo cumpleaños. Esto es muy contrario a la intuición.
A diferencia del ejemplo de “Hagamos un trato”, para este escenario, realmente no tenemos una buena explicación paso a paso que te dé una idea de esta sorprendente respuesta.
A partir de estos dos ejemplos, (tal vez) has visto que tus corazonadas originales no siempre pueden ser contadas para darte predicciones correctas de probabilidades.
No pensaremos más en estos ejemplos ya que son del extremo “más duro” del espectro de complejidad pero ojalá te hayan motivado a aprender más sobre la probabilidad y ¡no necesitas estar convencido de su solución para continuar!
En general, la probabilidad no siempre es intuitiva.
¿Necesitas una risa?
Mira este (divertido) video que tiene un excelente punto sobre “cómo la probabilidad NO funciona”: clip del Daily Show con Jon Stewart sobre el Gran Colisionador de Hadrones (5:58).
Es posible que los espectadores de otros países no puedan ver el clip desde esta fuente. Puede o no ser capaz de encontrarlo en línea a través de la búsqueda. Aquí está el resumen de la transcripción que a veces uso en clase para entender el punto (no es tan divertido pero creo que todavía puedes averiguar qué está mal aquí):
- John Oliver: Entonces, a grandes rasgos, ¿cuáles son las posibilidades de que el mundo sea destruido? (por el gran colisionador de hadrones) ¿Uno en un millón? ¿Uno en mil millones?
- Walter: Bueno, lo mejor que podemos decir ahora mismo es sobre una oportunidad de uno en dos.
- John Oliver: ¿50-50?
- Walter: Sí, 50-50... Es una oportunidad; es una oportunidad 50-50.
- John Oliver: Sigues volviendo a esta cosa del 50-50, es raro Walter.
- Walter: Bueno, si tienes algo que puede pasar y algo que no necesariamente va a suceder, o va a pasar o no va a suceder. Y, entonces, es... la mejor conjetura es 1 en 2.
- John Oliver: No estoy seguro así es como funciona la probabilidad, Walter.
Y... ¡John Oliver tiene razón! :-)
¿Qué es Probabilidad?
Objetivos de aprendizaje
LO 6.4: Relacionar la probabilidad de un evento con la probabilidad de que ocurra este evento.
Eventualmente necesitaremos desarrollar un enfoque más formal de la probabilidad, pero comenzaremos con una discusión informal de qué es la probabilidad.
La probabilidad es una descripción matemática de aleatoriedad e incertidumbre. Es una manera de medir o cuantificar la incertidumbre. Otra forma de pensar acerca de la probabilidad es que es el nombre oficial de “azar”.
La probabilidad es la probabilidad de que algo suceda
Una forma de pensar en la probabilidad es que es la probabilidad de que algo ocurra.
La probabilidad se utiliza para responder a los siguientes tipos de preguntas:
- ¿Cuál es la posibilidad de que llueva mañana?
- ¿Cuál es la posibilidad de que una acción suba de precio?
- ¿Cuál es la probabilidad de que tenga un ataque al corazón?
- ¿Cuál es la posibilidad de que viva más de 70 años?
- ¿Cuál es la probabilidad de que al rodar un par de dados, ruede dobles?
- ¿Cuál es la probabilidad de que gane la lotería?
- ¿Cuál es la probabilidad de que me vuelva diabético?
Cada uno de estos ejemplos tiene cierta incertidumbre. Para algunos, las posibilidades son bastante buenas, por lo que la probabilidad sería bastante alta. Para otros, las posibilidades no son muy buenas, por lo que la probabilidad es bastante baja (sobre todo ganar la lotería).
Ciertamente, la probabilidad de lluvia es diferente cada día, y es mayor durante algunas estaciones. Tu probabilidad de tener un ataque al corazón, o de vivir más de 70 años, depende de cosas como tu edad actual, tus antecedentes familiares y tu estilo de vida. Sin embargo, podrías usar tu intuición para predecir algunas de esas probabilidades con bastante precisión, mientras que otras quizás no tengas ningún instinto en absoluto.
Notación
Creemos que estarás de acuerdo en que la palabra probabilidad es un poco larga para incluirla en ecuaciones, gráficas y tablas, por lo que es costumbre usar alguna notación simplificada en lugar de la palabra completa.
Si queremos indicar “la probabilidad de que llueva mañana”, usamos la notación “P (lluvia mañana)”. Podemos abreviar la probabilidad de cualquier cosa. Si dejamos que A represente lo que deseamos encontrar la probabilidad, entonces P (A) representaría esa probabilidad.
Podemos pensar en “A” como un “evento”.
| NOTACIÓN | SENTIDO |
| P (ganar lotería) | la probabilidad de que una persona que tiene un boleto de lotería gane esa lotería |
| P (A) | la probabilidad de que ocurra el evento A |
| P (B) | la probabilidad de que ocurra el evento B |
PRINCIPIO: La “probabilidad” de un evento nos dice cuán probable es que ocurra el evento.
¿Qué valores puede tomar la probabilidad de un evento y qué nos dice el valor sobre la probabilidad de que ocurra el evento?
Video
Video: Propiedades Básicas de Probabilidad (0:53)
¿Recibí esto? : Propiedades Básicas de Probabilidad
PRINCIPIO: La probabilidad de que ocurra un evento está entre 0 y 1 o 0 ≤ P (A) ≤ 1.
Muchas personas prefieren expresar probabilidad en porcentajes. Dado que todas las probabilidades son decimales, cada una se puede cambiar a un porcentaje equivalente. Así, el último principio equivale a decir: “La probabilidad de que ocurra un evento está entre 0% y 100%”.
Las probabilidades se pueden determinar de dos maneras fundamentales. Sigue leyendo para saber cuáles son.
Determinar la probabilidad
Hay 2 formas fundamentales en las que podemos determinar la probabilidad:
- Teórico (también conocido como Clásico)
- Empírico (también conocido como Observacional)
Los métodos clásicos se utilizan para juegos de azar, como voltear monedas, rodar dados, hilanderos giratorios, ruedas de ruleta o loterías.
Las probabilidades en este caso están determinadas por el juego (o escenario) en sí y a menudo se encuentran con relativa facilidad usando lógica y/o reglas de probabilidad.
Aunque no nos centraremos en este tipo de probabilidad en este curso, mencionaremos algunos ejemplos para que pienses en la probabilidad y en cómo funciona.
EJEMPLO: Voltear una moneda

Una moneda tiene dos caras; usualmente las llamamos “cabezas” y “colas”.
Para una moneda “justa” (una que no esté ponderada de manera desigual y que no tenga imágenes idénticas en ambos lados) son igualmente probables las posibilidades de que un “giro” dé como resultado que cualquiera de los lados esté mirando hacia arriba.
Así, P (cabezas) = P (colas) = 1/2 o 0.5.
Dejando que H represente “cabezas”, podemos abreviar la probabilidad: P (H) = 0.5.
Las probabilidades clásicas también se pueden utilizar para situaciones más realistas y útiles.
Un uso práctico de un monedero sería que tú y tu compañero de cuarto decidieran al azar quién irá a recoger la pizza que pediste para la cena. Una expresión común es “Vamos a darle la vuelta”. Esto se debe a que una moneda puede ser utilizada para hacer una elección aleatoria con dos opciones. Muchos eventos deportivos comienzan con un volteo de monedas para determinar en qué lado del campo o cancha jugará cada equipo, o qué equipo tendrá el control del balón primero.
EJEMPLO: enrollar un troquel justo

Cada troquel tradicional (en forma de cubo) tiene seis lados, marcados en puntos con los números del 1 al 6.
En un dado “justo”, es igualmente probable que estos números terminen boca arriba cuando se enrolla el dado.
Así, P (1) = P (2) = P (3) = P (4) = P (5) = P (6) = 1/6 o aproximadamente 0.167.
Aquí, de nuevo, es un uso práctico de la probabilidad clásica.
Supongamos que seis personas salen a cenar. Quieres decidir al azar quién va a recoger el cheque y pagar por todos. Nuevamente, la P (cada persona) = 1/6.
EJEMPLO: Spinners
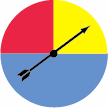
Este spinner en particular tiene tres colores, pero no es igualmente probable que cada color sea el resultado de un giro, ya que las porciones no son del mismo tamaño.
Dado que el azul es la mitad del spinner, P (azul) = 1/2. El rojo y el amarillo conforman la otra mitad de la hilandera y son del mismo tamaño. Así, P (rojo) = P (amarillo) = 1/4.
Supongamos que hay 2 estudiantes de primer año, 1 estudiante de segundo año y uno junior en un grupo de estudio. Desea seleccionar una persona. El P (F) = 2/4 = 1/2; P (S) = 1/4; y P (J) = 1/4, al igual que el spinner.
EJEMPLO: Seleccionar estudiantes
Supongamos que teníamos tres alumnos y deseábamos seleccionar uno de ellos al azar. Para ello es posible que cada persona escriba su nombre en una hoja de papel (del mismo tamaño), luego ponga los tres papeles en un sombrero y seleccione un papel del sombrero sin mirar.

Dado que estamos seleccionando aleatoriamente, es igualmente probable que cada uno sea elegido. Así, cada uno tiene una probabilidad de 1/3 de ser elegido.
Una pregunta de probabilidad un poco más complicada, pero más interesante, sería proponer seleccionar a 2 de los estudiantes que se muestran arriba, y preguntar: “¿Cuál es la probabilidad de que los dos estudiantes seleccionados sean de diferentes géneros?”
Ahora cambiaremos nuestra discusión a formas empíricas para determinar las probabilidades.
UNA PREGUNTA
Un solo giro de una moneda tiene un resultado incierto. Entonces, cada vez que se voltea una moneda, se desconoce el resultado de ese volteo hasta que ocurre el volteo.
Sin embargo, si volteas una y otra vez una moneda justa, ¿esperarías que P (H) sea exactamente 0.5? En otras palabras, ¿esperarías que haya el mismo número de resultados de “cabezas” que hay “colas”?
La siguiente actividad te permitirá descubrir la respuesta.
Aprende haciendo: Probabilidad empírica #1
La anterior actividad Aprender haciendo fue nuestro primer ejemplo de la segunda forma de determinar la probabilidad: los métodos empíricos (observacionales). En la actividad, determinamos que la probabilidad de obtener el resultado “cabezas” es de 0.5 volteando una moneda justa muchas, muchas veces.
Una segunda cuestión
Después de hacer este experimento, naturalmente me viene a la mente una pregunta importante. ¿Cómo sabríamos si la moneda no era justa? Ciertamente, los métodos clásicos de probabilidad nunca serían capaces de responder a esta pregunta. Además, los métodos clásicos nunca podrían decirnos el P (H) real. La única manera de responder a esta pregunta es realizando otro experimento.
La siguiente actividad te permitirá hacer precisamente eso.
Aprende haciendo: Probabilidad empírica #2
Entonces, este tipo de experimentos pueden verificar probabilidades clásicas y también pueden determinar cuándo los juegos de azar no están siguiendo prácticas justas. No obstante, su importancia real es responder a las preguntas de probabilidad que surgen cuando nos encontramos ante una situación que no sigue ningún patrón y no puede predeterminarse. En realidad, la mayoría de las probabilidades de interés para nosotros se ajustan a esta última descripción.
Para resumir hasta ahora
- La probabilidad es una forma de cuantificar la incertidumbre.
- Nos interesa la probabilidad de que ocurra un evento, la probabilidad de que ocurra el evento.
- La probabilidad de un evento oscila entre 0 y 1. Cuanto más cerca esté la probabilidad de 0, menos probable es que ocurra el evento. Cuanto más cerca esté la probabilidad de 1, más probable es que ocurra el evento.
- Existen dos formas de determinar la probabilidad: Teórica (Clásica) y Empírica (Observacional).
- Los métodos teóricos utilizan la naturaleza de la situación para determinar las probabilidades.
- Los métodos empíricos utilizan una serie de ensayos que producen resultados que no pueden predecirse de antemano (de ahí la incertidumbre).
Frecuencia relativa
Objetivos de aprendizaje
LO 6.5: Aplicar el enfoque de frecuencia relativa para estimar la probabilidad de un evento.
Si lanzamos una moneda, rodamos un dado, o giramos un spinner muchas veces, casi nunca alcanzamos las probabilidades teóricas exactas que sabemos que deberíamos obtener, pero podemos acercarnos bastante. Cuando ejecutamos una simulación o cuando usamos una muestra aleatoria y registramos los resultados, estamos usando probabilidad empírica. Esto a menudo se llama la definición de frecuencia relativa de probabilidad.
Aquí hay un ejemplo realista donde se utilizó el método de frecuencia relativa para encontrar las probabilidades:
EJEMPLO: Tipo sanguíneo
Los investigadores descubrieron a principios del siglo XX que la sangre humana viene en varios tipos (A, B, AB y O), y que algunos tipos son más comunes que otros. ¿Cómo podrían los investigadores determinar la probabilidad de un tipo de sangre en particular, digamos O?
El simple hecho de mirar a una o dos o a un puñado de personas no sería muy útil para determinar la probabilidad general de que una persona elegida al azar tenga el tipo de sangre O. Pero muestrear a muchas personas al azar, y encontrar la frecuencia relativa del tipo de sangre O que ocurre, proporciona una estimación adecuada.
Por ejemplo, ahora es bien sabido que la probabilidad de tipo sanguíneo O entre los blancos en Estados Unidos es de 0.45. Esto se encontró muestreando a muchos (digamos, 100,000) blancos en el país, encontrando que aproximadamente 45,000 de ellos tenían el tipo de sangre O, y luego usando la frecuencia relativa: 45,000/100,000 = 0.45 como estimación de la probabilidad para el evento “tener tipo de sangre O.”
(Comentario: Obsérvese que existen diferencias raciales y étnicas en las probabilidades de los tipos sanguíneos. Por ejemplo, la probabilidad de tipo sanguíneo O entre los negros en Estados Unidos es de 0.49, y la probabilidad de que una persona japonesa elegida al azar tenga el tipo de sangre O es de solo 0.3).
Revisemos el método de frecuencia relativa para encontrar probabilidades:
Para estimar la probabilidad del evento A, escrito P (A), podemos repetir el experimento aleatorio muchas veces y contar el número de veces que ocurre el evento A. Entonces P (A) se estima por la relación entre el número de veces que A ocurre con el número de repeticiones, lo que se denomina la frecuencia relativa del evento A.

¿Recibí esto? : Frecuencia relativa
Aprender haciendo: Frecuencia relativa
Entonces, hemos visto cómo funciona la idea de frecuencia relativa, y ojalá las actividades te hayan convencido de que la frecuencia relativa de un evento efectivamente se acerca a la probabilidad teórica de ese evento a medida que aumenta el número de repeticiones. A esto se le llama la Ley de Grandes Números.
La Ley de Grandes Números establece que a medida que aumenta el número de ensayos, la frecuencia relativa se convierte en la probabilidad real. Entonces, usando esta ley, a medida que aumenta el número de ensayos, la probabilidad empírica se acerca cada vez más a la probabilidad teórica.
PRINCIPIO: Ley de números grandes — La probabilidad real (o verdadera) de un evento (A) se estima por la frecuencia relativa con la que ocurre el evento en una larga serie de ensayos.
Applet interactivo: Ley de números grandes
Comentarios:
- Tenga en cuenta que el enfoque de frecuencia relativa proporciona solo una estimación de la probabilidad de un evento. Sin embargo, podemos controlar qué tan buena es esta estimación por el número de veces que repetimos el experimento aleatorio. Cuantas más repeticiones se realicen, más cerca se acerca la frecuencia relativa a la verdadera probabilidad del evento.
- Una pregunta interesante sería: “¿Cuántas veces necesito repetir el experimento aleatorio para que la frecuencia relativa esté, digamos, dentro de 0.001 de la probabilidad real del evento?” Volveremos a esa pregunta en el apartado de inferencia.
- Un comentario pedagógico: Aquí hemos introducido la frecuencia relativa en un enfoque más práctico, como método para estimar la probabilidad de un evento. Más tradicionalmente, la frecuencia relativa no se presenta como un método, sino como una definición:
Frecuencia relativa: (Definición) La probabilidad de un evento (A) es la frecuencia relativa con la que ocurre el evento en una larga serie de ensayos.
4. Son muchas las situaciones de interés en las que las circunstancias físicas no hacen evidente la probabilidad. De hecho, la mayoría de las veces es imposible encontrar la probabilidad teórica, y debemos usar probabilidades empíricas en su lugar.
Resumimos
La probabilidad es una forma de cuantificar la incertidumbre. En esta sección, definimos probabilidad como la probabilidad o probabilidad de que algo ocurra e introdujimos la notación básica de probabilidad como P (lotería ganadora).
Has visto que todas las probabilidades son valores entre 0 y 1, donde un evento sin posibilidad de ocurrir tiene una probabilidad de 0 y un evento que siempre ocurrirá tiene una probabilidad de 1.
Hemos discutido los dos métodos principales de cálculo de probabilidades
- Probabilidad teórica o clásica: utiliza la naturaleza de la situación para determinar las probabilidades
- Probabilidad empírica u observacional: utiliza una serie de ensayos que producen resultados que no pueden predecirse de antemano (de ahí la incertidumbre)
En nuestro curso nos centraremos en la probabilidad empírica y muchas veces calcularemos probabilidades a partir de una muestra usando frecuencias relativas.
Esto es útil en la práctica ya que la Ley de Números Grandes nos permite estimar la probabilidad real (o verdadera) de un evento por la frecuencia relativa con la que ocurre el evento en una larga serie de ensayos. Podemos recopilar esta información como datos y analizarlos utilizando estadísticas.

