Reglas Básicas de Probabilidad
- Última actualización
- 31 oct 2022
- Guardar como PDF
- Page ID
- 151226
( \newcommand{\kernel}{\mathrm{null}\,}\)
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Objetivos de aprendizaje
LO 6.4: Relacionar la probabilidad de un evento con la probabilidad de que ocurra este evento.
Objetivos de aprendizaje
LO 6.5: Aplicar el enfoque de frecuencia relativa para estimar la probabilidad de un evento.
Objetivos de aprendizaje
LO 6.6: Aplicar lógica básica y reglas de probabilidad para encontrar la probabilidad empírica de un evento.
Video
Video: Reglas Básicas de Probabilidad (25:17)
En el apartado anterior, se introdujo la probabilidad como una forma de cuantificar la incertidumbre que surge de la realización de experimentos utilizando una muestra aleatoria de la población de interés.
Vimos que la probabilidad de un evento (por ejemplo, el evento de que una persona elegida aleatoriamente tenga el tipo de sangre O) puede estimarse por la frecuencia relativa con la que ocurre el evento en una larga serie de ensayos. Entonces recolectaríamos datos de muchos individuos para estimar la probabilidad de que alguien tenga el tipo de sangre O.
En esta sección, estableceremos los métodos y principios básicos para encontrar probabilidades de eventos.
También cubriremos algunas de las reglas básicas de probabilidad que se pueden utilizar para calcular probabilidades.
Introducción
Comenzaremos con un ejemplo clásico de probabilidad de lanzar una moneda justa tres veces.
Dado que las cabezas y las colas son igualmente probables para cada tirada en este escenario, cada una de las posibilidades que pueden resultar de tres lanzamientos también será igualmente probable para que podamos enumerar todos los valores posibles y usar esta lista para calcular probabilidades.
Dado que nuestro enfoque en este curso está en los datos y la estadística (no en la probabilidad teórica), en la mayoría de nuestros problemas futuros utilizaremos un conjunto de datos resumido, generalmente una tabla de frecuencias o una tabla bidireccional, para calcular las probabilidades.
EJEMPLO: Lanza una moneda justa tres veces
Vamos a enumerar cada posible resultado (o posible resultado):
{HHH, THH, HTH, HHT, HTT, THT, TTH, TTT}
Ahora definamos los siguientes eventos:
Evento A: “No conseguir H”
Evento B: “Obteniendo exactamente una H”
Evento C: “Obteniendo al menos una H”
Obsérvese que cada evento es efectivamente una declaración sobre el resultado que va a producir el experimento. En la práctica, cada evento corresponde a alguna colección (subconjunto) de los posibles resultados.
Evento A: “No conseguir H” → TTT
Evento B: “Obtener exactamente una H” → HTT, THT, TTH
Evento C: “Obteniendo al menos una H” → HTT, THT, TTH, THH, HTH, HHT, HHH
Aquí hay una representación visual de los eventos A, B y C.
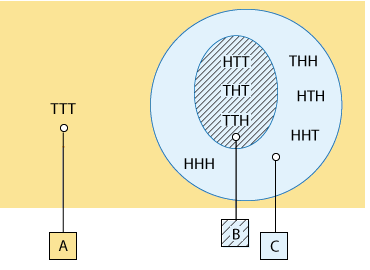
A partir de esta representación visual de los eventos, es fácil ver que el evento B está totalmente incluido en el evento C, en el sentido de que cada desenlace en el evento B también es un desenlace en el evento C. También, tenga en cuenta que el evento A se distingue de los eventos B y C, en el sentido de que no tienen resultado en común, o no se superponen. En este punto estas son sólo observaciones notables, pero como descubrirás más adelante, son muy importantes.
Y si agregamos el nuevo evento:
Evento D: “Obtener una T en el primer tiro” → THH, THT, TTH, TTT
¿Cómo quedaría si agregáramos el evento D al diagrama anterior? (Enlace a la respuesta)
Recuerde, dado que H y T son igualmente probables en cada lanzamiento, y dado que hay 8 resultados posibles, la probabilidad de cada resultado es 1/8.
Vea si puede responder las siguientes preguntas usando los diagramas y/o la lista de resultados para cada evento junto con lo que ha aprendido hasta ahora sobre la probabilidad.
Aprende haciendo: lanzar una moneda justa tres veces
Si pudiste responder esas preguntas correctamente, ¡probablemente tengas un buen instinto para calcular la probabilidad! Sigue leyendo para conocer cómo aplicaremos este conocimiento.
Si no, trataremos de ayudarte a desarrollar esta habilidad en esta sección.
Comentario:
- Tenga en cuenta que en el evento C, “Conseguir al menos una cabeza” solo hay un resultado posible que falta, “Obteniendo NO cabezas” = TTT. Volveremos a abordar esto cuando hablemos de reglas de probabilidad, en particular la regla del complemento. En este punto, solo queremos que pienses en cómo estos dos eventos son “opuestos” en este escenario.
Es MUY importante darse cuenta de que solo porque podamos enumerar los posibles resultados, esto no implica que cada resultado sea igualmente probable.
Este es el mensaje (divertido) en el clip de Daily Show que proporcionamos en la página anterior. Pero pensemos de nuevo en esto. En ese clip, Walter afirma que como hay dos posibles resultados, la probabilidad es de 0.5. Los dos posibles resultados son
- El mundo será destruido por el uso del gran colisionador de hadrones
- El mundo NO será destruido por el uso del gran colisionador de hadrones
Ojalá quede claro que estos dos resultados no son igualmente probables!!
Consideremos un ejemplo más común.
Ejemplo: Defectos de nacimiento
Supongamos que seleccionamos al azar tres hijos y nos interesa la probabilidad de que ninguno de los niños tenga defectos congénitos.
Utilizamos la notación D para representar a un niño nacido con un defecto congénito y N para representar al niño nacido sin defecto congénito. Podemos enumerar los posibles resultados tal como hicimos para el tiro de monedas, son:
{DDD, NDD, DND, DDN, DNN, NDN, NND, NNN}
¿Son igualmente probables los eventos DDD (los tres niños nacen con defectos congénitos) y NNN (ninguno de los niños nace con defectos congénitos)?
Debe ser razonable para usted que P (NNN) sea mucho mayor que P (DDD).
Esto se debe a que P (N) y P (D) no son eventos igualmente probables.
Es raro (ciertamente no 50%) que un niño seleccionado al azar nazca con un defecto congénito.
Reglas de Probabilidad
Ahora pasamos a aprender algunas de las reglas básicas de probabilidad.
Afortunadamente, estas reglas son muy intuitivas, y mientras se apliquen sistemáticamente, nos permitirán resolver problemas más complicados; en particular, aquellos problemas para los que nuestra intuición podría ser inadecuada.
Dado que la mayoría de las probabilidades que se le pedirá que encuentre se pueden calcular utilizando ambos
- lógica y conteo
y
- las reglas que vamos a estar aprendiendo,
damos como principio los siguientes consejos.
PRINCIPIO:
Si puedes calcular una probabilidad usando lógica y contando no NECESITAS una regla de probabilidad (aunque siempre se puede aplicar la regla correcta)
Probabilidad Regla Uno
Nuestra primera regla simplemente nos recuerda la propiedad básica de la probabilidad que ya aprendimos.
La probabilidad de un evento, que nos informa de la probabilidad de que ocurra, puede variar desde 0 (indicando que el evento nunca ocurrirá) hasta 1 (indicando que el evento es cierto).
Probabilidad Regla Uno:
- Para cualquier evento A, 0 ≤ P (A) ≤ 1.
NOTA: Un uso práctico de esta regla es que se puede utilizar para identificar como incorrecto cualquier cálculo de probabilidad que resulte ser más de 1 (o menor que 0).
Antes de pasar a las otras reglas, primero veamos un ejemplo que proporcionará un contexto para ilustrar las siguientes reglas.
Ejemplo: Tipos de sangre
Como se discutió anteriormente, toda la sangre humana puede ser tipificada como O, A, B o AB.
Además, la frecuencia de ocurrencia de estos tipos de sangre varía según los grupos étnicos y raciales.
Según el Centro de Sangre de la Universidad de Stanford (bloodcenter.stanford.edu), estas son las probabilidades de los tipos de sangre humana en Estados Unidos (la probabilidad para el tipo A se ha omitido a propósito):

Pregunta motivadora para la regla 2: Una persona en Estados Unidos es elegida al azar. ¿Cuál es la probabilidad de que la persona tenga el tipo de sangre A?
Respuesta Nuestra intuición nos dice que dado que los cuatro tipos de sangre O, A, B y AB agotan todas las posibilidades, sus probabilidades juntas deben sumar a 1, que es la probabilidad de un evento “cierto” (una persona tiene uno de estos 4 tipos de sangre para cierto).
Dado que las probabilidades de O, B y AB juntas suman 0.44 + 0.1 + 0.04 = 0.58, la probabilidad de tipo A debe ser la 0.42 restante (1 — 0.58 = 0.42):

Probabilidad Regla Dos
Este ejemplo ilustra nuestra segunda regla, que nos dice que la probabilidad de todos los resultados posibles juntos debe ser 1.
Regla de probabilidad dos:
La suma de las probabilidades de todos los resultados posibles es 1.
Este es un buen lugar para comparar y contrastar lo que estamos haciendo aquí con lo que aprendimos en la sección Análisis Exploratorio de Datos (EDA).
- Observe que en este problema nos estamos enfocando esencialmente en una sola variable categórica: el tipo de sangre.
- Resumimos esta variable arriba, ya que resumimos variables categóricas individuales en la sección EDA, enumerando qué valores toma la variable y con qué frecuencia los toma.
- En EDA usamos porcentajes, y aquí estamos usando probabilidades, pero los dos transmiten la misma información.
- En la sección EDA, aprendimos que un gráfico circular proporciona una visualización adecuada cuando una sola variable categórica está involucrada, y de manera similar podemos usarlo aquí (usando porcentajes en lugar de probabilidades):
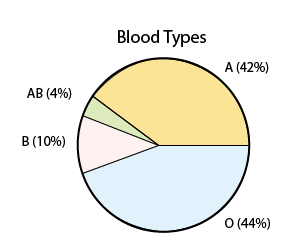
Aunque lo que estamos haciendo aquí es de hecho similar a lo que hemos hecho en la sección EDA, hay una diferencia sutil pero importante entre las situaciones subyacentes
- En EDA, resumimos los datos que se obtuvieron de una muestra de individuos para quienes se registraron valores de la variable de interés.
- Aquí, cuando presentamos la probabilidad de cada tipo de sangre, tenemos en mente a toda la población de personas en Estados Unidos, para lo cual presumimos conocer la frecuencia general de valores tomados por la variable de interés.
¿Conseguí esto? : Probabilidad Regla Dos
Probabilidad Regla Tres
En probabilidad y en sus aplicaciones, frecuentemente nos interesa conocer la probabilidad de que no ocurra un determinado evento.
Un punto importante a entender aquí es que “el evento A no ocurre” es un evento separado que consiste en todos los posibles resultados que no están en A y se llama “el evento complemento de A”.
Notación: escribiremos “no A” para denotar el evento de que A no ocurre. Aquí hay una representación visual de cómo el evento A y su evento de complemento “no A” juntos representan todos los resultados posibles.
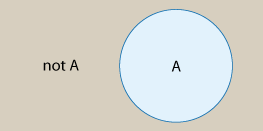
Comentario:
- Tal visualización visual se llama “diagrama de Venn”. Un diagrama de Venn es una forma sencilla de visualizar eventos y las relaciones entre ellos usando rectángulos y círculos.
La regla 3 trata de la relación entre la probabilidad de un evento y la probabilidad de su evento de complemento.
Dado que el evento A y el evento “no A” juntos conforman todos los resultados posibles, y dado que la regla 2 nos dice que la suma de las probabilidades de todos los resultados posibles es 1, la siguiente regla debe ser bastante intuitiva:
Regla de probabilidad tres (la regla del complemento):
- P (no A) = 1 — P (A)
- es decir, la probabilidad de que un evento no ocurra es 1 menos la probabilidad de que ocurra.
Ejemplo: Tipos de sangre
Volver al ejemplo del tipo de sangre:

Aquí hay alguna información adicional:
- Una persona con tipo A puede donar sangre a una persona con tipo A o AB.
- Una persona con tipo B puede donar sangre a una persona con tipo B o AB.
- Una persona con tipo AB solo puede donar sangre a una persona con tipo AB.
- Una persona con sangre tipo O puede donar a cualquier persona.
¿Cuál es la probabilidad de que una persona elegida al azar no pueda donar sangre a todos? En otras palabras, ¿cuál es la probabilidad de que una persona elegida al azar no tenga el tipo de sangre O? Tenemos que encontrar P (no O). Usando la Regla del Complemento, P (no O) = 1 — P (O) = 1 — 0.44 = 0.56. En otras palabras, 56% de la población estadounidense no tiene el tipo de sangre O:
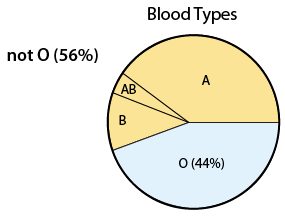
Claramente, también podríamos encontrar P (no O) directamente agregando las probabilidades de B, AB y A.
Comentario:
- Obsérvese que la Regla del Complemento, P (no A) = 1 — P (A) puede reformularse como P (A) = 1 — P (no A).
- P (no A) = 1 — P (A)
- se puede reformular como P (A) = 1 — P (no A).
- Esta manipulación algebraica aparentemente trivial tiene una aplicación importante, y en realidad captura la fuerza de la regla del complemento.
- En algunos casos, cuando encontrar P (A) directamente es muy complicado, podría ser mucho más fácil encontrar P (no A) y luego simplemente restarlo de 1 para obtener el P (A) deseado.
- Pronto volveremos a este comentario y brindaremos ejemplos adicionales.
¿Conseguí esto? : Probabilidad Regla Tres
Comentarios:
- La regla del complemento puede ser útil siempre que sea más fácil calcular la probabilidad del complemento del evento en lugar del evento en lugar del evento en sí.
- Observe, nuevamente usamos la frase “al menos uno”.
- Ahora hemos visto que el complemento de “al menos uno...” es “ninguno...” o “no...” (como mencionamos anteriormente en términos de que los eventos son “opuestos”).
- En la actividad anterior vemos que
- P (NINGUNO de estos dos efectos secundarios) = 1 — P (al menos uno de estos dos efectos secundarios)
- Esta es una aplicación común de la regla del complemento que a menudo se puede reconocer por la frase “al menos una” en el problema.
Probabilidades que involucran múltiples eventos
A menudo nos interesará encontrar probabilidades que involucren múltiples eventos como
- P (A o B) = P (ocurre el evento A o el evento B ocurre o ocurren ambos)
- P (A y B) = P (ocurre tanto el evento A como el evento B)
Un problema común con la terminología se relaciona con cómo solemos pensar en “o” en nuestra vida diaria. Por ejemplo, cuando un padre le dice a su hijo en una juguetería “¿Quieres el juguete A o el juguete B?” , esto significa que el niño va a conseguir un solo juguete y tiene que elegir entre ellos. Conseguir ambos juguetes no suele ser una opción.
En contraste:
En probabilidad, “OR” significa uno o el otro o ambos.
y así P (A o B) = P (ocurre el evento A o el evento B ocurre o ocurren AMBOS)
Dicho esto, cabe señalar que hay algunos casos en los que simplemente es imposible que ambos eventos ocurran al mismo tiempo.
Probabilidad Regla Cuatro
La distinción entre eventos que pueden ocurrir juntos y los que no pueden es importante.
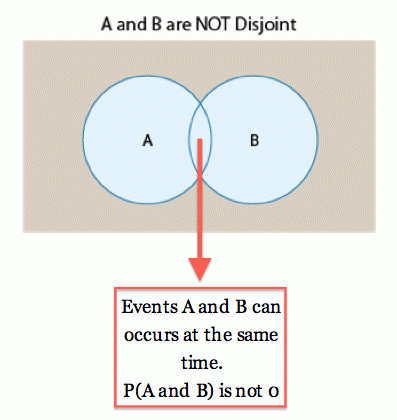
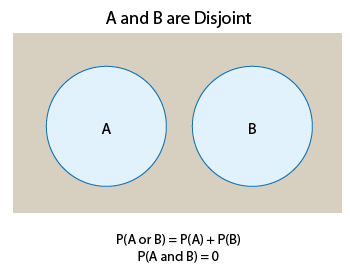
Disjuntos: Dos eventos que no pueden ocurrir al mismo tiempo se denominan disjuntos o mutuamente excluyentes. (Vamos a utilizar disjoint.)
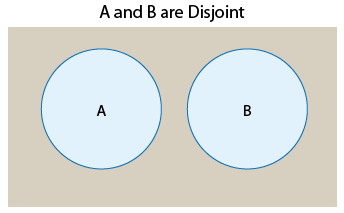
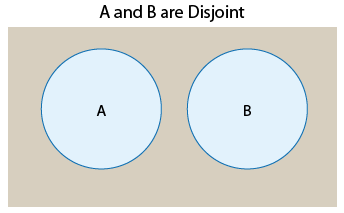
Debe quedar claro a partir de la imagen que
- en el primer caso, donde los eventos NO son disjuntos, P (A y B) ≠ 0
- en el segundo caso, donde los eventos SON disjuntos, P (A y B) = 0.
Aquí hay dos ejemplos:
EJEMPLO:
Considere los dos eventos siguientes:
A — una persona elegida al azar tiene el tipo de sangre A, y
B — una persona elegida al azar tiene el tipo de sangre B.
En raras ocasiones, es posible que una persona tenga más de un tipo de sangre fluyendo por sus venas, pero para nuestros propósitos, vamos a suponer que cada persona puede tener sólo un tipo de sangre. Por lo tanto, es imposible que los eventos A y B ocurran juntos.
- Los eventos A y B son DISJUNTOS
Por otro lado...
EJEMPLO:
Considere los dos eventos siguientes:
A — una persona elegida al azar tiene el tipo de sangre A
B — una persona elegida al azar es una mujer.
En este caso, es posible que los eventos A y B ocurran juntos.
- Los eventos A y B NO SON DISJUNTOS.
Los diagramas de Venn sugieren que otra forma de pensar sobre eventos disjuntos versus no disjuntos es que los eventos disjuntos no se superponen. No comparten ninguno de los posibles resultados, y por lo tanto no pueden suceder juntos.
Por otro lado, los eventos que no son disjuntos se superponen en el sentido de que comparten algunos de los posibles resultados y por lo tanto pueden ocurrir al mismo tiempo.
Ahora comenzamos con una regla simple para encontrar P (A o B) para eventos disjuntos.
Regla de Probabilidad Cuatro (La Regla de Suma para Eventos Disjuntos):
- Si A y B son eventos disjuntos, entonces P (A o B) = P (A) + P (B).
Comentario:
- Al tratar con probabilidades, la palabra “o” siempre estará asociada a la operación de adición; de ahí el nombre de esta regla, “La Regla de Adición”.
EJEMPLO: Tipos sanguíneos
Recordemos el ejemplo del tipo de sangre:

Aquí hay alguna información adicional
- Una persona con tipo A puede donar sangre a una persona con tipo A o AB.
- Una persona con tipo B puede donar sangre a una persona con tipo B o AB.
- Una persona con tipo AB puede donar sangre a una persona con tipo AB
- Una persona con sangre tipo O puede donar a cualquier persona.
¿Cuál es la probabilidad de que una persona elegida al azar sea un donante potencial para una persona con tipo de sangre A?
Por la información brindada, sabemos que ser donante potencial para una persona con tipo de sangre A significa tener el tipo de sangre A u O.
Por lo tanto, necesitamos encontrar P (A u O). Dado que los eventos A y O son disjuntos, podemos usar la regla de adición para eventos disjuntos para obtener:
- P (A u O) = P (A) + P (O) = 0.42 + 0.44 = 0.86.
Es fácil ver por qué agregar la probabilidad realmente tiene sentido.
Si el 42% de la población tiene el tipo de sangre A y el 44% de la población tiene el tipo de sangre O,
- entonces 42% + 44% = 86% de la población tiene ya sea el tipo de sangre A u O, y así son potenciales donantes a una persona con tipo de sangre A.
Este razonamiento sobre por qué la regla de adición tiene sentido se puede visualizar usando el gráfico circular a continuación:
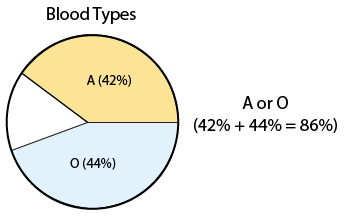
Aprende haciendo: Regla de probabilidad cuatro
Comentario:
- La Regla de Adición para Eventos Disjuntos, naturalmente, puede extenderse a más de dos eventos disjuntos. Tomemos tres, por ejemplo. Si A, B y C son tres eventos disgregados
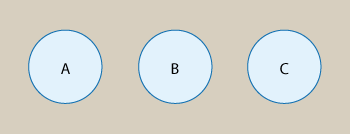
después P (A o B o C) = P (A) + P (B) + P (C). La regla es la misma para cualquier número de eventos disjuntos.
¿Conseguí esto? : Probabilidad Regla Cuatro
Ya terminamos con la primera versión de la Regla de Adición (Regla cuatro) que es la versión restringida a eventos disjuntos. Antes de cubrir la segunda versión, primero debemos discutir P (A y B).
Encontrar P (A y B) usando Lógica
Pasamos ahora al cálculo
- P (A y B) = P (ocurre tanto el evento A como el evento B)
Posteriormente, discutiremos las reglas para calcular P (A y B).
Primero, queremos ilustrar que no se necesita una regla siempre que se pueda determinar la respuesta a través de la lógica y el conteo.
Caso especial:
Hay un caso especial para el que sabemos a qué equivale P (A y B) sin aplicar ninguna regla.
Aprender haciendo: Encontrar P (A y B) #1
Entonces, si los eventos A y B son disjuntos, entonces (por definición) P (A y B) = 0. Pero, ¿y si los hechos no son disgregantes?
Recordemos que la regla 4, la Regla de Adición, tiene dos versiones. Uno está restringido a eventos disjuntos, que ya hemos cubierto, y trataremos la versión más general más adelante en este módulo. Lo mismo será cierto de probabilidades que involucren Y
No obstante, salvo en casos especiales, confiaremos en LOGIC para encontrar P (A y B) en este curso.
Antes de cubrir cualquier regla formal, veamos un ejemplo donde los eventos no son disjuntos.
EJEMPLO: Estado periodontal y género
Aprende haciendo: Estatus Periodontal y Género
Nos gusta hacer preguntas de probabilidad similares al ejemplo anterior (usando una tabla bidireccional basada en datos) ya que esto le permite hacer conexiones entre estos temas y le ayuda a mantener algo de lo que ha aprendido sobre los datos frescos en su mente.
Precaución
Recuerda, ¡nuestro objetivo principal en este curso es analizar datos de la vida real!
Probabilidad Regla Cinco
Ahora estamos listos para pasar a la versión extendida de la Regla de Adición.
En esta sección, vamos a aprender a encontrar P (A o B) cuando A y B no son necesariamente disjuntos.
- Llamaremos a esta versión extendida la “Regla General de Adición” y la declararemos como Regla de Probabilidad Cinco.
Comenzaremos por exponer la regla y dar un ejemplo similar a los tipos de problemas que generalmente pedimos en este curso. Entonces presentaremos un ejemplo más otro donde no tenemos los datos brutos de una muestra para trabajar de.
Como vimos en ejemplos anteriores, cuando los dos hechos no son disjuntos, hay cierta superposición entre los hechos.
- Si simplemente sumamos las dos probabilidades juntas, obtendremos la respuesta equivocada porque ¡hemos contado alguna “probabilidad” dos veces!
- Así, debemos restar esta probabilidad “extra” para llegar a la respuesta correcta. El diagrama de Venn y las tablas bidireccionales son útiles para visualizar esta idea.
Esta regla es más general ya que funciona para cualquier par de eventos (incluso eventos disjuntos). Nuestro consejo sigue siendo tratar de responder a la pregunta usando la lógica y contando siempre que sea posible, de lo contrario, debemos ser extremadamente cuidadosos para elegir la regla correcta para el problema.
PRINCIPIO:
Si puedes calcular una probabilidad usando lógica y contando no NECESITAS una regla de probabilidad (aunque siempre se puede aplicar la regla correcta)
Observe que, si A y B son disjuntos, entonces P (A y B) = 0 y la regla 5 reduce a la regla 4 para este caso especial.
Repasemos el último ejemplo:
EJEMPLO: Estado periodontal y género
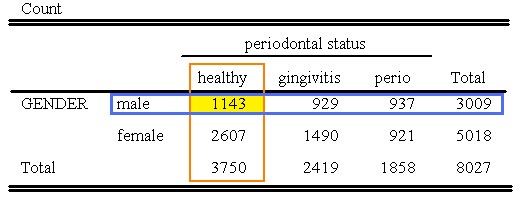
Considera seleccionar aleatoriamente un individuo de entre los representados en la siguiente tabla con respecto al estado periodontal de los individuos y su género. El estado periodontal se refiere a la enfermedad de las encías donde los individuos se clasifican como sanos, tienen gingivitis o tienen enfermedad periodontal.

Repasemos lo que hemos aprendido hasta el momento. Podemos calcular cualquier probabilidad en este escenario si podemos determinar cuántos individuos satisfacen el evento o combinación de eventos.
- P (Macho) = 3009/8027 = 0.3749
- P (Hembra) = 5018/8027 = 0.6251
- P (Saludable) = 3750/8027 = 0.4672
- P (No Saludable) = P (Gingivitis o Perio) = (2419 + 1858) /8027 = 4277/8027 = 0.5328 También
podríamos, calcular esto usando la regla del complemento: 1 — P (Saludable)
También encontramos anteriormente que
- P (Masculino Y Sano) = 1143/8027 = 0.1424
Recordar regla 5, P (A o B) = P (A) + P (B) — P (A y B). Ahora usamos esta regla para calcular P (Masculino O Saludable)
- P (Masculino o Sano) = P (Masculino) + P (Sano) — P (Masculino y Sano) = 0.3749 + 0.4672 — 0.1424 = 0.6997 o aproximadamente 70%
Resolvimos esta cuestión antes simplemente contando cuántos individuos son Masculinos o Saludables o ambos. La siguiente imagen ilustra los valores que necesitamos combinar. Tenemos que contar
- Todos los machos
- Todos los individuos sanos
- PERO, ¡no contar a nadie dos veces!!
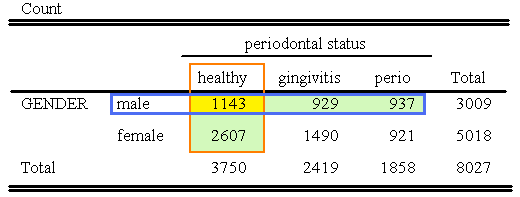
Usando este enfoque lógico encontraríamos
- P (Masculino o Sano) = (1143 + 929 + 937 + 2607) /8027 = 5616/8027 = 0.6996
Tenemos una diferencia menor en nuestras respuestas en el último decimal debido al redondeo que se produjo cuando calculamos P (Masculino), P (Saludable) y P (Masculino y Saludable) y luego aplicamos la regla 5.
Claramente la respuesta es efectivamente la misma, alrededor del 70%. Si llevamos nuestras respuestas a más decimales o si usamos las fracciones originales, podríamos eliminar por completo esta pequeña discrepancia.
Veamos un último ejemplo para ilustrar la regla de probabilidad 5 cuando se necesita la regla, es decir, cuando no tenemos datos reales.
EJEMPLO: ¡Entrega importante!
Es vital que un determinado documento llegue a su destino en el plazo de un día. Para maximizar las posibilidades de entrega puntual, se envían dos copias del documento utilizando dos servicios, el servicio A y el servicio B. Se sabe que las probabilidades de entrega puntual son:
- 0.90 para el servicio A (P (A) = 0.90)
- 0.80 para el servicio B (P (B) = 0.80)
- 0.75 para ambos servicios estando a tiempo (P (A y B) = 0.75)
(Obsérvese que A y B son n ot disjuntos. Pueden ocurrir junto con probabilidad 0.75.)
Los diagramas de Venn a continuación ilustran las probabilidades P (A), P (B) y P (A y B) [no dibujadas a escala]:
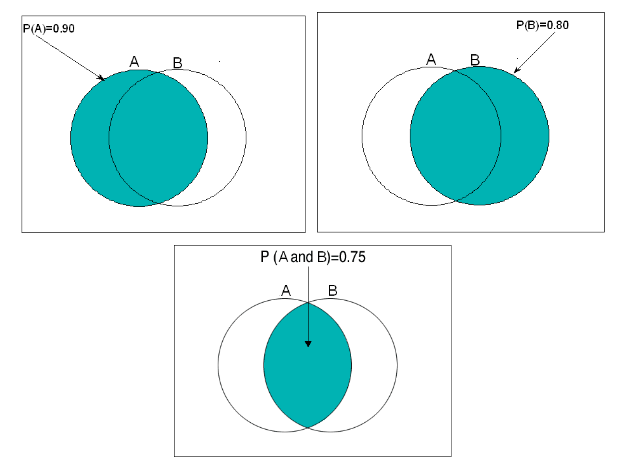
En el contexto de este problema, la pregunta obvia de interés es:
- ¿Cuál es la probabilidad de entrega puntual del documento utilizando esta estrategia (de enviarlo a través de ambos servicios)?
El documento llegará a su destino a tiempo siempre y cuando sea entregado a tiempo por el servicio A o por el servicio B o por ambos servicios. Es decir, cuando ocurre el evento A o ocurre el evento B o ocurren ambos. Entonces...
P (entrega a tiempo usando esta estrategia) = P (A o B), que se representa por la región sombreada en el siguiente diagrama:
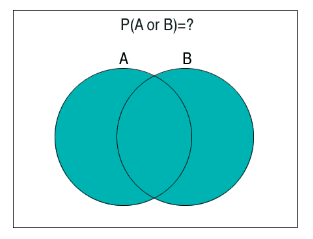
Ahora podemos
- utilizar los tres diagramas de Venn que representan P (A), P (B) y P (A y B)
- para ver que podemos encontrar P (A o B) sumando P (A) (representado por el círculo izquierdo) y P (B) (representado por el círculo derecho),
- luego restando P (A y B) (representado por el solapamiento), ya que lo incluimos dos veces, una como parte de P (A) y una vez como parte de P (B).
Esto se muestra en la siguiente imagen:
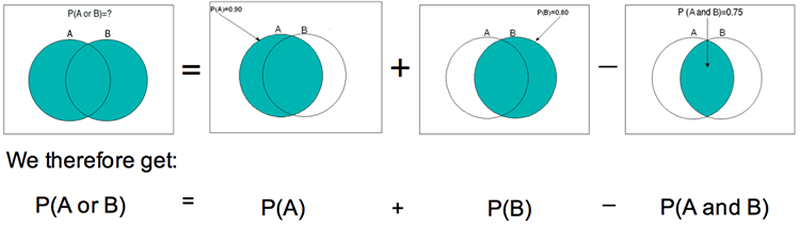
Si aplicamos esto a nuestro ejemplo, encontramos que:
- P (A o B) = P (entrega a tiempo usando esta estrategia) = 0.90 + 0.80 — 0.75 = 0.95.
Así que nuestra estrategia de utilizar dos servicios de entrega aumenta nuestra probabilidad de entrega a tiempo a 0.95.
Si bien los diagramas de Venn fueron geniales para visualizar la Regla General de Adición, en casos como estos es mucho más fácil mostrar la información y trabajar con una tabla bidireccional de probabilidades, tanto como examinamos la relación entre dos variables categóricas en la sección Análisis Exploratorio de Datos.
Simplemente te mostraremos la tabla, no cómo la derivamos ya que no se te pedirá que hagas esto por nosotros. Deberías poder ver que alguna lógica y simple sución/resta es todo lo que usamos para rellenar la tabla a continuación.
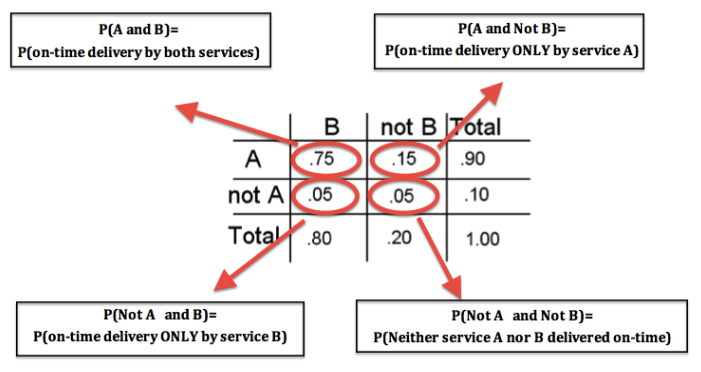
Al usar una tabla de dos vías, debemos recordar mirar toda la fila o columna para encontrar probabilidades generales que involucren solo A o solo B.
- P (A) = 0.90 significa que en el 90% de los casos en que se utiliza el servicio A, entrega el documento a tiempo. Para encontrar esto nos fijamos en la probabilidad total para la fila que contiene A. Al encontrar P (A), no sabemos si B sucede o no.
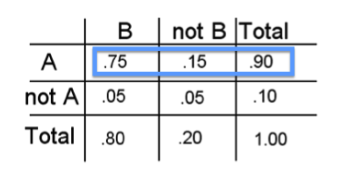
- P (B) = 0.80 significa que en el 80% de los casos en que se utiliza el servicio B, entrega el documento a tiempo. Para encontrar esto nos fijamos en la probabilidad total para la columna que contiene B. Al encontrar P (B), no sabemos si A sucede o no.
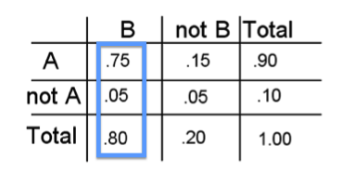
Comentario
- Cuando se utilizaron tablas bidireccionales en la sección Análisis Exploratorio de Datos (EDA), fue para registrar valores de dos variables categóricas para una muestra concreta de individuos.
- En contraste, la información en una tabla de probabilidad bidireccional es para toda una población, y los valores son bastante abstractos.
- Si hubiéramos tratado algo como el ejemplo de entrega en la sección EDA, habríamos registrado los números reales de entregas a tiempo (y no a tiempo) para muestras de documentos enviados por correo con el servicio A o B.
- En esta sección se presentan como conocidas las probabilidades a largo plazo.
- Presumiblemente, las probabilidades reportadas en este ejemplo de entrega se basaron en frecuencias relativas registradas en muchas repeticiones.
Applet interactivo: Diagrama de probabilidad de Venn
Regla de redondeo para probabilidad:
Siga las siguientes pautas generales en este curso. En caso de duda llevar más decimales. Si especificamos dar exactamente lo que se solicita.
- En general debes llevar probabilidades a al menos 4 decimales para los pasos intermedios.
- A menudo redondeamos nuestra respuesta final a dos o tres decimales.
- Para probabilidades extremadamente pequeñas, es importante tener 1 o dos dígitos significativos (dígitos distintos de cero), como 0.000001 o 0.000034, etc.
Muchos paquetes de computadora pueden mostrar valores extremadamente pequeños usando notación científica como
- 58×10 -5 o 1.58 E -5 para representar 0.0000158
Resumimos
Hasta ahora en nuestro estudio de la probabilidad, se le ha introducido la naturaleza a veces contraintuitiva de la probabilidad y los fundamentos que subyacen a la probabilidad, como una frecuencia relativa.
También te dimos algunas herramientas para ayudarte a encontrar las probabilidades de eventos, es decir, las reglas de probabilidad.
Probablemente notó que la sección de probabilidad era significativamente diferente de las dos secciones anteriores; tiene un componente técnico/matemático mucho mayor, por lo que los resultados tienden a ser más de la naturaleza “correcta o incorrecta”.
En la sección Análisis Exploratorio de Datos, en su mayor parte, la computadora se encargó del aspecto técnico de las cosas, y nuestras tareas fueron decirle que hiciera lo correcto y luego interpretar los resultados.
En probabilidad, hacemos el trabajo de principio a fin, desde elegir la herramienta adecuada (regla) para usar, hasta usarla correctamente, hasta interpretar los resultados.
Aquí un resumen de las reglas que hemos presentado hasta el momento.
1. La Regla de Probabilidad #1 establece:
- Para cualquier evento A, 0 ≤ P (A) ≤ 1
2. La Regla de Probabilidad #2 establece:
- La suma de las probabilidades de todos los resultados posibles es 1
3. La Regla del Complemento (#3) establece que
- P (no A) = 1 — P (A)
o cuando se reorganizan
- P (A) = 1 — P (no A)
Esta última representación de la Regla del Complemento es especialmente útil cuando necesitamos encontrar probabilidades de eventos del tipo “al menos uno de...”
4. La Regla General de Adición (#5) establece que para dos hechos cualesquiera,
- P (A o B) = P (A) + P (B) — P (A y B),
donde, por P (A o B) nos referimos a P (A ocurre o B ocurre o ambos).
En el caso especial de eventos disjuntos, eventos que no pueden ocurrir juntos, la Regla General de Adición puede reducirse a la Regla de Adición para Eventos Disjuntos (#4), que es
- P (A o B) = P (A) + P (B). *
*Úselo solo cuando esté CONVENCIDO de que los eventos son disjuntos (NO se superponen)
5. La versión restringida de la regla de adición (para eventos disjuntos) se puede extender fácilmente a más de dos eventos.
6. Hasta el momento, solo hemos encontrado P (A y B) usando lógica y contando en ejemplos simples

