Probabilidad e independencia condicionales
- Última actualización
- Guardar como PDF
- Page ID
- 151225
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Objetivos de aprendizaje
LO 6.4: Relacionar la probabilidad de un evento con la probabilidad de que ocurra este evento.
Objetivos de aprendizaje
LO 6.5: Aplicar el enfoque de frecuencia relativa para estimar la probabilidad de un evento.
Objetivos de aprendizaje
LO 6.6: Aplicar lógica básica y reglas de probabilidad para encontrar la probabilidad empírica de un evento.
Revisión: Unidad 1 Caso C-C
- En particular la idea de porcentajes condicionales será equivalente a la idea de probabilidades condicionales discutida en esta sección.
Video
Video: Probabilidad e Independencia Condicionales (28:13)
En el último apartado, establecimos algunas de las reglas básicas de probabilidad, que incluían:
- Propiedades Básicas de Probabilidad (Regla Uno y Regla Dos)
- La Regla del Complemento (Regla Tres)
- La Regla de Adición para Eventos Disjuntos (Regla Cuatro)
- La Regla General de Adición para la cual no es necesario que los hechos sean desarticulados (Regla Cinco)
Para completar nuestro conjunto de reglas, todavía requerimos dos Reglas de Multiplicación para encontrar P (A y B) y los conceptos importantes de eventos independientes y probabilidad condicional.
Primero introduciremos la idea de eventos independientes, luego introduciremos la Regla de Multiplicación para eventos independientes que da una manera de encontrar P (A y B) en los casos en que los eventos A y B son independientes.
A continuación definiremos la probabilidad condicional y la usaremos para formalizar nuestra definición de eventos independientes, que inicialmente se presenta únicamente de manera intuitiva.
Luego desarrollaremos la Regla General de Multiplicación, una regla que nos dirá cómo encontrar P (A y B) en los casos en que los eventos A y B no sean necesariamente independientes.
Concluiremos con una discusión sobre las aplicaciones probabilísticas en las ciencias de la salud.
Eventos Independientes
Objetivos de aprendizaje
LO 6.7: Determina si dos eventos son independientes o dependientes y justifica tu conclusión.
Comenzamos con una definición verbal de eventos independientes (posteriormente usaremos notación de probabilidad para definir esto con mayor precisión).
Eventos Independientes:
- Se dice que dos eventos A y B son independientes si el hecho de que haya ocurrido un evento no afecta la probabilidad de que ocurra el otro evento.
- Si ocurre o no un evento afecta la probabilidad de que ocurra el otro evento, entonces se dice que los dos eventos son dependientes.
Aquí hay algunos ejemplos:
EJEMPLO:
El bolsillo de una mujer contiene dos cuartos y dos monedas de cinco centavos.
Ella extrae al azar una de las monedas y, después de mirarla, la reemplaza antes de recoger una segunda moneda.
Sea Q1 el evento de que la primera moneda sea un cuarto y Q2 sea el evento de que la segunda moneda sea un cuarto.
¿Los eventos Q1 y Q2 son independientes?
- ¿Por qué?
Dado que la primera moneda que se seleccionó es reemplazada, si ocurrió o no Q1 (es decir, si la primera moneda era un cuarto) no tiene efecto sobre la probabilidad de que la segunda moneda sea un cuarto, P (Q2).
En cualquier caso (haya ocurrido el primer trimestre o no), al seleccionar la segunda moneda, tiene en el bolsillo:
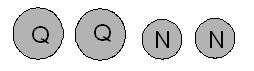
y por lo tanto el P (Q2) = 2/4 = 1/2 independientemente de si Q1 ocurrió.
EJEMPLO:
El bolsillo de una mujer contiene dos cuartos y dos monedas de cinco centavos.
Ella extrae al azar una de las monedas, y sin volver a colocarla en su bolsillo, toma una segunda moneda.
Como antes, que Q1 sea el evento de que la primera moneda sea un cuarto, y Q2 sea el evento de que la segunda moneda sea un cuarto.
¿Los eventos Q1 y Q2 son independientes?
- Q1 y Q2 no son independientes. Son dependientes. ¿Por qué?
Dado que la primera moneda que se seleccionó no es reemplazada, si ocurrió Q1 (es decir, si la primera moneda era un cuarto) sí afecta la probabilidad de que la segunda moneda sea un cuarto, P (Q2).
Si ocurrió el primer trimestre (es decir, la primera moneda era un cuarto), entonces cuando la mujer está seleccionando la segunda moneda, tiene en su bolsillo:
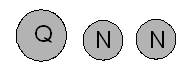
- En este caso, P (Q2) = 1/3.
No obstante, si el primer trimestre no ha ocurrido (es decir, la primera moneda no era un cuarto, sino un níquel), entonces cuando la mujer está seleccionando la segunda moneda, tiene en su bolsillo:
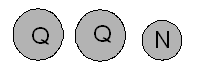
- En este caso, P (Q2) = 2/3.
En estos dos últimos ejemplos, en realidad podríamos haber hecho algún cálculo para verificar si los dos eventos son o no independientes o no.
A veces solo podemos usar el sentido común para guiarnos en cuanto a si dos eventos son independientes. Aquí hay un ejemplo.
EJEMPLO:
Dos personas son seleccionadas simultáneamente y al azar de todas las personas en Estados Unidos.
Que B1 sea el evento de que una de las personas tenga ojos azules y B2 sea el evento de que la otra persona tenga ojos azules.
En este caso, ya que fueron elegidos al azar, si uno de ellos tiene ojos azules no afecta la probabilidad de que el otro tenga ojos azules, y por lo tanto B1 y B2 son independientes.
Por otro lado...
EJEMPLO:
Una familia tiene 4 hijos, dos de los cuales son seleccionados al azar.
Que B1 sea el evento de que un niño tenga ojos azules, y B2 sea el evento de que el otro niño elegido tenga ojos azules.
En este caso, B1 y B2 no son independientes, ya que sabemos que el color de ojos es hereditario.
Así, el hecho de que un niño tenga o no ojos azules aumentará o disminuirá las posibilidades de que el otro niño tenga ojos azules, respectivamente.
Comentarios:
- Es bastante común que los estudiantes se confundan inicialmente sobre la distinción entre la idea de eventos disjuntos y la idea de eventos independientes. El propósito de este comentario (y la actividad que le sigue) es ayudar a los estudiantes a desarrollar una mayor comprensión sobre estas ideas muy diferentes.
La idea de eventos disjuntos es sobre si es posible o no que los eventos ocurran al mismo tiempo (vea los ejemplos en la página para Reglas Básicas de Probabilidad).
La idea de eventos independientes se trata de si los eventos se afectan o no entre sí en el sentido de que la ocurrencia de un evento afecta la probabilidad de la ocurrencia del otro (ver los ejemplos anteriores).
La siguiente actividad trata de la distinción entre estos conceptos.
El propósito de esta actividad es ayudarte a fortalecer tu comprensión sobre los conceptos de eventos disjuntos y eventos independientes, y la distinción entre ellos.
Aprende haciendo: Eventos Independientes
Resumimos las tres partes de la actividad:
- En el Ejemplo 1: A y B no son disjuntas e independientes
- En el Ejemplo 2: A y B no son disjuntas y no independientes
- En el Ejemplo 3: A y B son disjuntas y no independientes.
¿Por qué dejamos de lado el caso cuando los hechos son disgregantes e independientes?
¡La razón es que este caso NO EXISTE!
| A y B Independiente | A y B no independientes | |
| A y B Disjuntos | NO EXISTE | Ejemplo 3 |
| A y B no disjuntos | Ejemplo 1 | Ejemplo 2 |
Si los eventos son disjuntos entonces no deben ser independientes, es decir, deben ser eventos dependientes.
¿Por qué es eso?
- Recordemos: Si A y B son disjuntos entonces no pueden pasar juntos.
- En otras palabras, A y B siendo eventos disjuntos implica que si ocurre el evento A entonces B no ocurre y viceversa.
- Bueno... si ese es el caso, saber que el evento A ha ocurrido cambia drásticamente la probabilidad de que ocurra el evento B —esa probabilidad es cero.
- Esto implica que A y B no son independientes.
Ahora que entendemos la idea de eventos independientes, finalmente podemos llegar a reglas para encontrar P (A y B) en el caso especial en el que los eventos A y B son independientes.
Posteriormente presentaremos una versión más general para su uso cuando los eventos no sean necesariamente independientes.
Regla de Multiplicación para Eventos Independientes (Regla Seis)
Objetivos de aprendizaje
LO 6.8: Aplicar la regla de multiplicación para eventos independientes para calcular P (A y B) para eventos independientes.
Pasamos ahora a las reglas para calcular
- P (A y B) = P (ocurre tanto el evento A como el evento B)
comenzando con la regla de multiplicación para eventos independientes.
Usando un diagrama de Venn, podemos visualizar “A y B”, que se representa por la superposición entre los eventos A y B:
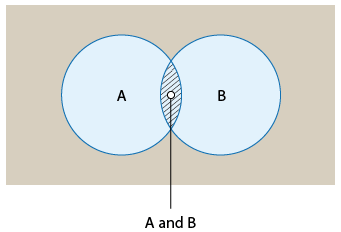
Regla de Probabilidad Seis (La Regla de Multiplicación para Eventos Independientes):
- Si A y B son dos eventos INDEPENDIENTES, entonces P (A y B) = P (A) * P (B).
Comentario:
- Al tratar con reglas de probabilidad, la palabra “y” siempre estará asociada a la operación de multiplicación; de ahí el nombre de esta regla, “La Regla de Multiplicación”.
EJEMPLO:
Recordemos el ejemplo del tipo de sangre:

Dos personas son seleccionadas simultáneamente y al azar de todas las personas en Estados Unidos.
¿Cuál es la probabilidad de que ambos tengan el tipo sanguíneo O?
- Dejar O1= “la persona 1 tiene el tipo de sangre O” y
- O2= “la persona 2 tiene el tipo de sangre O”
Necesitamos encontrar P (O1 y O2)
Ya que fueron elegidos simultáneamente y al azar, el tipo de sangre de uno no tiene ningún efecto sobre el tipo de sangre del otro. Por lo tanto, O1 y O2 son independientes, y podemos aplicar la Regla 6:
- P (O1 y O2) = P (O1) * P (O2) = 0.44 * 0.44 = 0.1936.
¿Recibí esto? : Regla Seis de Probabilidad
Comentarios:
- Ahora tenemos una Regla de Adición que dice
P (A o B) = P (A) + P (B) para eventos disconjuntos,
y una Regla de Multiplicación que dice
P (A y B) = P (A) * P (B) para eventos independientes.
El propósito de este comentario es señalar la magnitud de P (A o B) y de P (A y B) relativa a cualquiera de las probabilidades individuales.
Dado que las probabilidades nunca son negativas, la probabilidad de un evento u otro siempre es al menos tan grande como cualquiera de las probabilidades individuales.
Dado que las probabilidades nunca son mayores que 1, la probabilidad de un evento y otro generalmente implica multiplicar números que son menores a 1, por lo tanto nunca puede ser mayor que cualquiera de las probabilidades individuales.
Aquí hay un ejemplo:
EJEMPLO:
Considera el evento A que una persona elegida al azar tiene el tipo de sangre A.
Modifíquelo a un evento más general —que una persona elegida al azar tenga el tipo de sangre A o B— y la probabilidad aumente.
Modifíquelo a un evento más específico (o restrictivo) —que no solo una persona elegida aleatoriamente tenga el tipo de sangre A, sino que de dos personas elegidas simultáneamente al azar, la persona 1 tendrá tipo A y la persona 2 tendrá tipo B— y la probabilidad disminuye.
Es importante mencionar esto para desarraigar un concepto erróneo común.
- La palabra “y” se asocia en nuestras mentes con “agregar más cosas”. Por lo tanto, algunos estudiantes piensan incorrectamente que P (A y B) debe ser mayor que cualquiera de las probabilidades individuales, mientras que en realidad es menor, ya que es un evento más específico (restrictivo).
- Además, la palabra “o” se asocia en nuestras mentes con “tener que elegir entre” o “perder algo”, y por lo tanto algunos estudiantes piensan incorrectamente que P (A o B) debería ser menor que cualquiera de las probabilidades individuales, mientras que en realidad es mayor, ya que es un evento más general.
Prácticamente, puedes usar este comentario para comprobarte a la hora de resolver problemas.
Por ejemplo, si resuelves un problema que involucra “o”, y la probabilidad resultante es menor que cualquiera de las probabilidades individuales, entonces sabes que has cometido un error en alguna parte.
¿Recibí esto? : Comparando P (A y B) con P (A o B)
Comentario:
- La regla de probabilidad seis se puede utilizar como prueba para ver si dos eventos son independientes o no.
- Si puede encontrar fácilmente P (A), P (B) y P (A y B) usando lógica o se le proporcionan estos valores, entonces podemos probar eventos independientes usando la regla de multiplicación para eventos independientes:
SI P (A) *P (B) = P (A y B) ENTONCES A y B son eventos independientes, de lo contrario, son eventos dependientes.
Como has visto, las tres últimas reglas que hemos introducido (la Regla del Complemento, las Reglas de Adición y la Regla de Multiplicación para Eventos Independientes) se utilizan frecuentemente para resolver problemas.
Antes de pasar a nuestra siguiente regla, aquí hay dos comentarios que te ayudarán a usar estas reglas en tipos más amplios de problemas y de manera más efectiva.
Comentario:
- Como mencionamos anteriormente, la Regla de Adición para eventos Disjuntos (regla cuatro) puede extenderse a más de dos eventos disjuntos.
- De igual manera, la Regla de Multiplicación para eventos independientes (regla seis) puede extenderse a más de dos eventos independientes.
- Entonces si A, B y C son tres eventos independientes, por ejemplo, entonces P (A y B y C) = P (A) * P (B) * P (C).
- Estas extensiones son bastante sencillas, siempre y cuando recuerdes que “o” nos obliga a sumar, mientras que “y” nos obliga a multiplicar.
EJEMPLO:
Tres personas son elegidas simultáneamente y al azar.
¿Cuál es la probabilidad de que los tres tengan el tipo de sangre B?
Utilizaremos la notación habitual de B1, B2 y B3 para los eventos en los que las personas 1, 2 y 3 tengan el tipo de sangre B, respectivamente.
Necesitamos encontrar P (B1 y B2 y B3). Resolvamos esto juntos:
Aprende haciendo: Extendiendo la regla de probabilidad seis
Aquí hay otro ejemplo que podría resultar bastante sorprendente.
EJEMPLO:
Una moneda justa es arrojada 10 veces. ¿Cuál de los siguientes dos resultados es más probable?
(a) HHHHHHHHH
b) HTTHHTHTTH
Aprende haciendo: ¿Un resultado sorprendente usando la regla de probabilidad seis?
De hecho, son igualmente probables. Los 10 lanzamientos son independientes, por lo que usaremos la Regla de Multiplicación para Eventos Independientes:
- P (HHHHHHHHH) = P (H) * P (H) *... *P (H) = 1/2 * 1/2 *... * 1/2 = (1/2) 10
- P (HTTHHTHTTH) = P (H) * P (T) *... * P (H) = 1/2 * 1/2 *... * 1/2 = (1/2) 10
Aquí está la idea:
Nuestro experimento aleatorio aquí es arrojar una moneda 10 veces.
- Te puedes imaginar lo enorme que es el espacio muestral.
- En realidad, hay 1.024 resultados posibles en este experimento, todos los cuales son igualmente probables.
Por lo tanto,
- si bien es cierto que es más probable que obtenga un resultado que tenga 5 cabezas y 5 colas que un resultado que solo tenga cabezas
ya que solo hay un resultado posible que da a todas las cabezas
y muchos resultados posibles que dan 5 cabezas y 5 colas
- si estamos comparando 2 resultados específicos como lo hacemos aquí, son igualmente probables.
Comentarios IMPORTANTES:
- Solo usa la regla de multiplicación para eventos independientes, regla seis, que dice P (A y B) = P (A) P (B) si estás seguro de que los dos eventos son independientes.
- La regla de probabilidad seis SOLO es cierta para eventos independientes.
- Al encontrar P (A o B) usando la regla general de suma: P (A) + P (B) — P (A y B),
- NO use la regla de multiplicación para eventos independientes para calcular P (A y B), use solo lógica y conteo.
Probabilidad Condicional (Regla Siete)
Objetivos de aprendizaje
LO 6.9: Aplicar reglas lógicas o de probabilidad para calcular probabilidades condicionales, P (A|B), e interpretarlas en contexto.
Ahora vamos a introducir el concepto de probabilidad condicional.
La idea aquí es que las probabilidades de ciertos eventos pueden verse afectadas por si han ocurrido o no otros eventos.
El término “condicional” se refiere al hecho de que tendremos condiciones adicionales, restricciones, u otra información cuando se nos pida calcular este tipo de probabilidad.
Ilustremos esta idea con un ejemplo sencillo:
EJEMPLO:
Todos los alumnos de cierta preparatoria fueron encuestados, luego clasificados según el género y si tenían alguna de sus orejas perforadas:
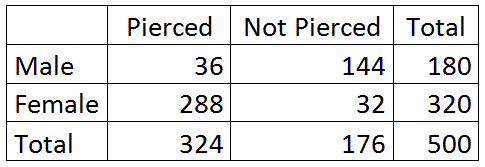
(Tenga en cuenta que esta es una tabla bidireccional de recuentos que se introdujo por primera vez cuando hablamos de la relación entre dos variables categóricas.
No es de extrañar que lo estemos utilizando nuevamente en este ejemplo, ya que efectivamente tenemos aquí dos variables categóricas:
- Género: M o F (en nuestra notación, “no M”)
- Pierced: Sí o No
Supongamos que un alumno es seleccionado al azar de la escuela.
- Que M y no M denoten los eventos de ser masculino y femenino, respectivamente,
- y E y no E denotan los eventos de tener orejas perforadas o no, respectivamente.
¿Cuál es la probabilidad de que el alumno tenga alguna de sus orejas perforadas?
Dado que un alumno es elegido al azar del grupo de 500 alumnos, de los cuales 324 son perforados,
- P (E) = 324/500 = 0.648
¿Cuál es la probabilidad de que el estudiante sea varón?
Dado que se elige al azar a un alumno del grupo de 500 alumnos, de los cuales 180 son varones,
- P (M) = 180/500 = 0.36.
¿Cuál es la probabilidad de que el estudiante sea varón y tenga la oreja (s) perforada (s)?
Dado que un alumno es escogido al azar del grupo de 500 alumnos de los cuales 36 son varones y tienen la (s) oreja (s) perforada (s),
- P (M y E) = 36/500 = 0.072
Ahora algo nuevo:
Dado que el alumno que fue elegido es varón, ¿cuál es la probabilidad de que tenga una o ambas orejas perforadas?
En este punto, se requiere una nueva notación, para expresar la probabilidad de un determinado evento dado que otro evento se sostiene.
Escribiremos
- “la probabilidad de tener alguna oreja perforada (E), dado que un estudiante es masculino (M)”
- como P (E | M).
Unas palabras sobre esta nueva notación:
- El evento cuya probabilidad buscamos (en este caso E) se escribe primero,
- la línea vertical significa la palabra “dado” o “condicionado”,
- y el evento que se da (en este caso M) se escribe después del signo “|”.
Llamamos a esta probabilidad el
- probabilidad condicional de tener alguna de las orejas perforadas, dado que un estudiante es varón:
- evalúa la probabilidad de tener orejas perforadas bajo la condición de ser varón.
Ahora para encontrar la probabilidad, observamos que elegir entre solo los varones en la escuela esencialmente altera el espacio muestral de todos los alumnos de la escuela a todos los estudiantes varones de la escuela.
El número total de resultados posibles ya no es de 500, sino que ha cambiado a 180.
De esos 180 machos, 36 tienen oreja (s) perforada (s), y así:
- P (E | M) = 36/180 = 0.20.
Una buena ilustración visual de esta probabilidad condicional es proporcionada por la tabla bidireccional:
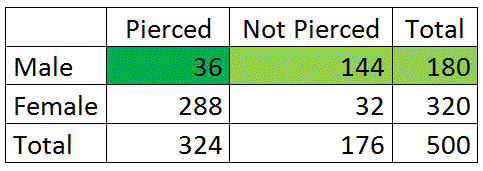
lo que nos muestra que la probabilidad condicional en este ejemplo es la misma que los porcentajes condicionales que calculamos de nuevo en la sección 1. En la ilustración visual anterior, es claro que estamos calculando un porcentaje de fila.
EJEMPLO:
Consideremos el ejemplo penetrante, donde se da la siguiente tabla bidireccional,
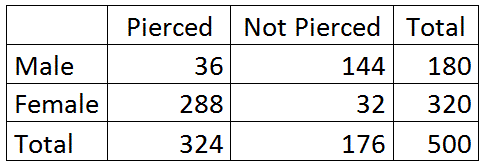
Recordemos también que M representa el evento de ser macho (“no M” representa ser hembra), y E representa el evento de tener una o ambas orejas perforadas.
¿Recibí esto? : Probabilidad Condicional
Otra forma de visualizar la probabilidad condicional es usar un diagrama de Venn:
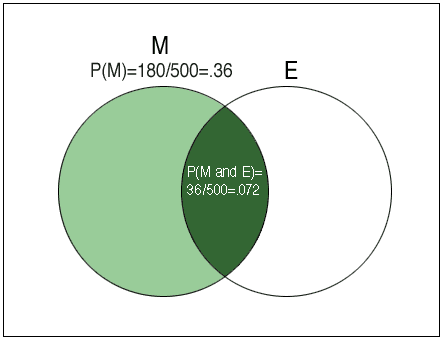
Tanto en la tabla bidireccional como en el diagrama de Venn,
- el espacio muestral reducido (compuesto solo por machos) es verde claro sombreado,
- y dentro de este espacio muestral, el evento de interés (tener las orejas perforadas) está sombreado de color verde más oscuro.
La tabla bidireccional ilustra la idea a través de recuentos, mientras que el diagrama de Venn convierte los recuentos en probabilidades, que se presentan como regiones en lugar de celdas.
Podemos trabajar con recuentos, como se presenta en la tabla de dos vías, para escribir
- P (E | M) = 36/180.
O podemos trabajar con probabilidades, tal como se presenta en el diagrama de Venn, escribiendo
- P (E | M) = (36/500)/(180/500).
Vamos a querer, sin embargo, escribir nuestra expresión formal de probabilidades condicionales en términos de otras probabilidades, ordinarias y por lo tanto la definición de probabilidad condicional crecerá a partir del diagrama de Venn.
Observe que
- P (E | M) = (36/500)/(180/500) = P (M y E)/P (M).
Regla de probabilidad siete (regla de probabilidad condicional):
- La probabilidad condicional del evento B, dado evento A, es P (B | A) = P (A y B)/P (A)
Comentarios:
- Tenga en cuenta que cuando evaluamos la probabilidad condicional, siempre dividimos por la probabilidad del evento dado. La probabilidad de ambos va en el numerador.
- La fórmula anterior se mantiene siempre que P (A) > 0, ya que no podemos dividir por 0. En otras palabras, no debemos buscar la probabilidad de un suceso dado que se ha producido un suceso imposible.
Veamos cómo podemos usar esta fórmula en la práctica:
EJEMPLO:
En la etiqueta “Información para el Paciente” de cierto antidepresivo, se afirma que con base en algunos ensayos clínicos,
- hay un 14% de probabilidad de experimentar problemas de sueño conocidos como insomnio (denotar este evento por I),
- hay un 26% de probabilidad de experimentar cefalea (denotar este evento por H),
- y existe un 5% de probabilidad de experimentar ambos efectos secundarios (I y H).
a) Supongamos que el paciente experimenta insomnio; ¿cuál es la probabilidad de que el paciente también experimente dolor de cabeza?
Ya que sabemos (o se da) que el paciente experimentó insomnio, estamos buscando P (H | I).
Según la definición de probabilidad condicional:
- P (H | I) = P (H e I)/P (I) = 0.05/0.14 = 0.357.
b) Supongamos que el fármaco induce cefalea en un paciente; ¿cuál es la probabilidad de que también induzca insomnio?
Aquí, se nos da que el paciente experimentó dolor de cabeza, por lo que estamos buscando P (I | H).
Usando la definición
- P (I | H) = P (I y H)/P (H) = 0.05/0.26 = 0.1923.
Comentario:
- Obsérvese que las respuestas a (a) y (b) anteriores son distintas.
- En general, P (A | B) no es igual a P (B | A). Volveremos e ilustraremos este punto más adelante.
Ahora que hemos introducido la probabilidad condicional, pruebe la demostración interactiva a continuación que utiliza un diagrama de Venn para ilustrar las probabilidades básicas que hemos estado discutiendo.
Ahora también puedes investigar las probabilidades condicionales.
Applet interactivo: Probabilidad condicional
Eventos Independientes (Parte 2)
Objetivos de aprendizaje
LO 6.7: Determina si dos eventos son independientes o dependientes y justifica tu conclusión.
Como vimos en la sección Análisis Exploratorio de Datos, siempre que una situación involucra más de una variable, generalmente es de interés determinar si las variables están o no relacionadas.
En probabilidad, hablamos de eventos independientes, y antes dijimos que dos eventos A y B son independientes si el evento A que ocurre no afecta la probabilidad de que ocurra el evento B.
Ahora que hemos introducido la probabilidad condicional, podemos formalizar la definición de independencia de eventos y desarrollar cuatro formas sencillas de verificar si dos eventos son independientes o no.
Introduciremos estos “controles de independencia” usando ejemplos, y luego resumiremos.
EJEMPLO:
Consideremos nuevamente la mesa bidireccional para los 500 alumnos de una preparatoria en particular, clasificados según el género y si tienen o no una o ambas orejas perforadas.
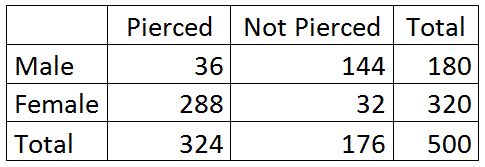
¿Esperarías que esas dos variables estén relacionadas?
- Es decir, ¿esperarías tener orejas perforadas para depender de si el alumno es masculino o femenino?
- O, para decirlo de otra manera, ¿el conocer el género de un estudiante afectaría la probabilidad de que se perforen los oídos del estudiante?
Para responder a esto, podemos comparar la probabilidad general de tener orejas perforadas con la probabilidad condicional de tener orejas perforadas, dado que un estudiante es varón.
Nuestra intuición nos diría que este último debería ser menor:
- los estudiantes varones tienden a no tener las orejas perforadas, mientras que las estudiantes femeninas sí.
En efecto, para los estudiantes en general, la probabilidad de tener orejas perforadas (evento E) es
- P (E) = 324/500 = 0.648.
Pero la probabilidad de tener orejas perforadas dado que un estudiante es varón es solo
- P (E | M) = 36/180 = 0.20.
Como anticipamos, P (E | M) es menor que P (E).
La probabilidad de que un estudiante tenga orejas perforadas cambia (en este caso, disminuye) cuando sabemos que el estudiante es masculino, y por lo tanto los eventos E y M son dependientes.
Recuerden, si E y M fueran independientes, saber o no saber que el alumno es varón no habría hecho la diferencia... pero sí.
El ejemplo anterior ilustra que un método para determinar si dos eventos son independientes es comparar P (B | A) y P (B).
- Si los dos son iguales (es decir, saber o no saber si A ha ocurrido no tiene ningún efecto sobre la probabilidad de que ocurra B) entonces los dos eventos son independientes.
- De lo contrario, si la probabilidad cambia dependiendo de si sabemos que A ha ocurrido o no, entonces los dos eventos no son independientes.
De igual manera, usando el mismo razonamiento, podemos comparar P (A | B) y P (A).
EJEMPLO:
Recordemos la actividad de efectos secundarios (desde la parte inferior de la página Reglas Básicas de Probabilidad.).
En la etiqueta “Información para el Paciente” de cierto antidepresivo, se afirma que con base en algunos ensayos clínicos,
- hay un 14% de probabilidad de experimentar problemas de sueño conocidos como insomnio (denotar este evento por I),
- hay un 26% de probabilidad de experimentar cefalea (denotar este evento por H),
- y existe un 5% de probabilidad de experimentar ambos efectos secundarios (I y H).
¿Los dos efectos secundarios son independientes entre sí?
Para verificar si los dos efectos secundarios son independientes, comparemos P (H | I) y P (H).
En la parte anterior de esta sección, encontramos que
- P (H | I) = P (H e I)/P (I) = 0.05/0.14 = 0.357,
- mientras que P (H) = 0.26.
Saber que un paciente experimentó insomnio aumenta la probabilidad de que también experimente dolor de cabeza de 0.26 a 0.357.
Por lo tanto, la conclusión es que los dos efectos secundarios no son independientes, son dependientes.
Alternativamente, podríamos haber comparado P (I | H) con P (I).
- P (I) = 0.14,
- y anteriormente encontramos que P (I | H) = P (I y H)/P (H) = 0.05/0.26 = 0.1923,
Nuevamente, como los dos no son iguales, podemos concluir que los dos efectos secundarios I y H son dependientes.
Comentario:
- Recordemos el ejemplo de orejas perforadas. Se comprobó la independencia de los eventos M (ser macho) y E (tener orejas perforadas) comparando P (E) con P (E | M).
Un método alternativo para verificar la dependencia sería comparar P (E | M) con P (E | no M) [igual que P (E | F)].
En nuestro caso, P (E | M) = 36/180 = 0.2, mientras que P (E | no M) = 288/320 = 0.9, y como los dos son muy diferentes, podemos decir que los eventos E y M no son independientes.
En general, otro método para verificar la independencia de los eventos A y B es comparar P (B | A) y P (B | no A).
En otras palabras, dos eventos son independientes si la probabilidad de un evento no cambia ya sea que sepamos que el otro evento ha ocurrido o sabemos que el otro evento no ha ocurrido.
Se puede demostrar que P (B | A) y P (B | no A) diferirían siempre que P (B) y P (B | A) difieran, por lo que esta es otra forma perfectamente legítima de establecer dependencia o independencia.
Antes de establecer una regla general para la independencia, consideremos un ejemplo que ilustrará otro método que podemos usar para verificar si dos eventos son independientes:
EJEMPLO:
Se encuestó a un grupo de 100 estudiantes universitarios sobre su género y si habían decidido una especialización.
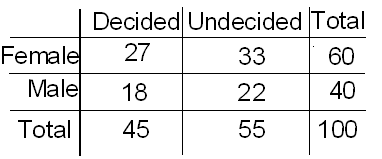
De improviso, no necesariamente tendríamos ninguna razón de peso para esperar que decidir sobre una especialización dependiera del género de un estudiante.
Podemos verificar la independencia comparando la probabilidad general de ser decidido con la probabilidad de decidirse dado que un estudiante es femenino:
- P (D) = 45/100 = 0.45 y P (D | F) = 27/60 = 0.45.
El hecho de que los dos sean iguales nos dice que, como cabría esperar, decidir sobre una mayor es independiente del género.
Ahora abordemos el tema de la independencia de una manera diferente: primero, podemos señalar que la probabilidad general de ser decididos es 45/100 = 0.45.
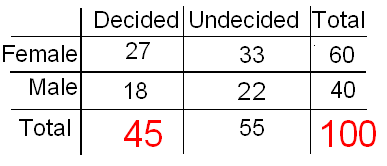
Y la probabilidad general de ser mujer es de 60/100 = 0.60.
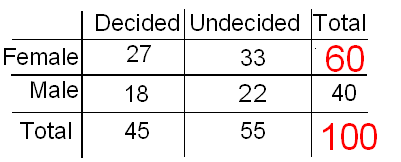
Si se decide es independiente del género, entonces 45% del 60% de la clase que son mujeres debe tener una especialización decidida;
es decir, la probabilidad de ser femenina y decidida debe ser igual a la probabilidad de ser femenina multiplicada por la probabilidad de ser decidida.
Si los eventos F y D son independientes, deberíamos tener P (F y D) = P (F) * P (D).
De hecho, P (F y D) = 27/100 = 0.27 = P (F) * P (D) = 0.45 * 0.60.
Esto confirma nuestra verificación alterna de independencia.
En general, otro método para verificar la independencia de los eventos A y B es
- comparar P (A y B) a P (A) * P (B).
- Si los dos son iguales, entonces A y B son independientes, de lo contrario los dos no son independientes.
Resumamos todos los métodos posibles que hemos visto para verificar la independencia de los eventos en una sola regla:
Pruebas para Eventos Independientes: Dos eventos A y B son independientes si se cumple alguno de los siguientes:
- P (B | A) = P (B)
- P (A | B) = P (A)
- P (B | A) = P (B | no A)
- P (A y B) = P (A) * P (B)
Comentario:
- Estas diversas igualdades resultan ser equivalentes, de manera que si una igualdad se mantiene, todas son iguales, y si una igualdad no se sostiene, todas no son iguales. (Este es el caso por la misma razón que conocer uno de los valores P (A y B), P (A y no B), P (no A y B), o P (no A y no B), junto con P (A) y P (B), permite determinar las celdas restantes de una tabla de probabilidad bidireccional.)
- Por lo tanto, para verificar si los eventos A y B son independientes o no, basta con verificar únicamente si se mantiene una de las cuatro igualdades —la que sea más fácil para usted.
El propósito de la siguiente actividad es practicar la verificación de la independencia de dos eventos utilizando los cuatro métodos diferentes posibles que hemos proporcionado, y ver que todos ellos nos llevarán a la misma conclusión, independientemente de cuál de los cuatro métodos que usemos.
Aprende haciendo: Pruebas para eventos independientes
Regla General de Multiplicación (Regla Ocho)
Objetivos de aprendizaje
LO 6.10: Usa la regla general de multiplicación para calcular P (A y B) para cualquier evento A y B.
Ahora que tenemos una comprensión de las probabilidades condicionales y podemos expresarlas con notación concisa, y tener una comprensión más formal de lo que significa que dos eventos sean independientes, finalmente podemos establecer la Regla General de Multiplicación, una regla formal para encontrar P (A y B) que se aplica a dos eventos cualesquiera, ya sean independientes o dependientes.
Comenzamos con un ejemplo que contrasta P (A y B) para casos independientes y dependientes.
EJEMPLO:
Supongamos que eliges dos cartas al azar de entre cuatro cartas que constan de uno de cada palo: palo, diamante, corazón y pala, donde la primera carta es reemplazada antes de que se elija la segunda carta.
¿Cuál es la probabilidad de elegir un palo y luego un diamante?
Debido a que el muestreo se realiza con reemplazo, el hecho de que se escoja o no un diamante en la segunda selección es independiente de si se ha seleccionado o no un palo en la primera selección.
La regla 6, la regla de multiplicación para eventos independientes, nos dice que:
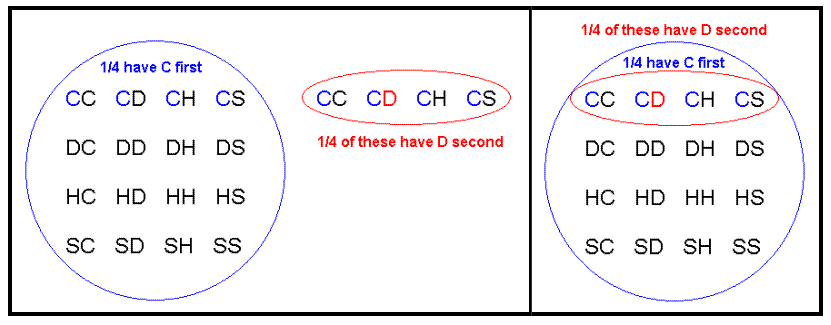
- P (C1 y D2) = P (C1) * P (D2) = 1/4 * 1/4 = 1/16.
Aquí denotamos el evento “club escogido en primera selección” como C1 y el evento “diamante recogido en segunda selección” como D2.
La siguiente pantalla muestra que 1/4 de las veces elegiremos primero un club, y de estos tiempos, 1/4 resultará en un diamante en la segunda selección: 1/4 * 1/4 = 1/16 de las selecciones tendrán primero un club y luego un diamante.
EJEMPLO:
Supongamos que eliges dos cartas al azar de entre cuatro cartas que constan de uno de cada palo: palo, diamante, corazón y pala, sin reemplazar la primera carta antes de que se elija la segunda carta.
¿Cuál es la probabilidad de elegir un palo y luego un diamante?
La probabilidad en este caso no es 1/4 * 1/4 = 1/16.
- Debido a que el muestreo se realiza sin reemplazo, por lo que el hecho de que se escoja o no un diamante en la segunda selección depende de lo que se escogió en la primera selección.
- Por ejemplo, si se escogió un diamante en la primera selección, ¡la probabilidad de otro diamante es cero!
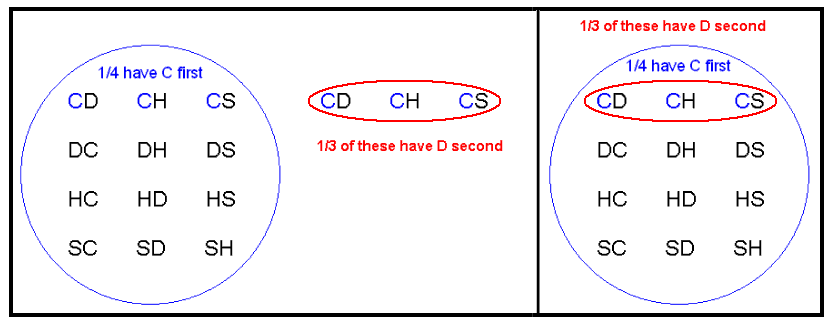
- Al igual que en el ejemplo anterior, 1/4 de las veces elegiremos primero un club.
- Pero como el club ha sido removido, 1/3 de estas selecciones con un club primero tendrán un diamante en segundo lugar.
La probabilidad de un palo y luego un diamante es 1/4*1/3=1/12.
- Esta es la probabilidad de conseguir un club primero, multiplicada por la probabilidad de conseguir un diamante en segundo lugar, dado que un club fue elegido primero.
Usando la notación de probabilidades condicionales, podemos escribir
- P (C1 y D2) = P (C1) * P (D2 | C1) = 1/4 * 1/3 = 1/12.
Para los eventos independientes A y B, tuvimos la regla P (A y B) = P (A) * P (B).
Debido a la independencia, para encontrar la probabilidad de A y B, podríamos multiplicar la probabilidad de A por la simple probabilidad de B, ya que la ocurrencia de A no tendría ningún efecto sobre la probabilidad de que B ocurra.
Ahora bien, para los eventos A y B que pueden ser dependientes, para encontrar la probabilidad de A y B, multiplicamos la probabilidad de A por la probabilidad condicional de B, tomando en cuenta que A ha ocurrido.
Así, nuestra regla general de multiplicación se establece de la siguiente manera:
Regla General de Multiplicación — Regla de Probabilidad Ocho:
- Para dos eventos cualesquiera A y B, P (A y B) = P (A) * P (B | A)
Comentarios:
- Tenga en cuenta que aunque la motivación para esta regla fue encontrar P (A y B) cuando A y B no son independientes, esta regla es general en el sentido de que si A y B resultan ser independientes, entonces P (B | A) = P (B) es verdadera, y volvemos a la Regla 6 — la Regla de Multiplicación para Eventos Independientes: P (A y B) = P (A) * P (B).
- La Regla General de Multiplicación es solo la definición de probabilidad condicional disfrazada. Recordemos la definición de probabilidad condicional: P (B | A) = P (A y B)/P (A) Vamos a aislar P (A y B) multiplicando ambos lados de la ecuación por P (A), y obtenemos: P (A y B) = P (A) * P (B | A). Eso es... esta es la Regla General de Multiplicación.
- La Regla General de Multiplicación es útil cuando dos eventos, A y B, ocurren en etapas, primero A y luego B (como la selección de las dos cartas en el ejemplo anterior). Pensarlo de esta manera hace que la Regla General de Multiplicación sea muy intuitiva. Para que ocurran tanto A como B primero necesitas que ocurra A (lo que ocurre con probabilidad P (A)), y luego necesitas que B ocurra, sabiendo que A ya ha ocurrido (lo que ocurre con probabilidad P (B | A)).
¿Recibí esto? : La regla general de multiplicación
Veamos otro ejemplo más realista:
EJEMPLO:
En cierta región, una de cada mil personas (0.001) está infectada por el virus VIH que causa el SIDA.
- Las pruebas para detectar la presencia del virus son bastante precisas pero no perfectas.
- Si alguien realmente tiene VIH, la probabilidad de dar positivo es de 0.95.
Que H denote el evento de tener VIH, y T el evento de dar positivo.
a) Expresar la información que se da en la problemática en términos de los hechos H y T.
- “una de cada mil personas (0.001) de todos los individuos están infectados con VIH” → P (H) = 0.001
- “Si alguien realmente tiene VIH, la probabilidad de dar positivo es de 0.95” → P (T | H) =0.95
b) Utilizar la Regla General de Multiplicación para encontrar la probabilidad de que alguien escogido al azar de la población tenga VIH y dé positivo.
- P (H y T) = P (H) * P (T | H) = 0.001*0.95 = 0.00095.
(c) Si alguien tiene VIH, ¿cuál es la probabilidad de que la prueba sea negativa? Aquí necesitamos encontrar P (no T | H).
- La Regla del Complemento funciona con probabilidades condicionales siempre y cuando condicionemos el mismo evento, por lo tanto:
- P (no T | H) = 1 — P (T | H) = 1 — 0.95 = 0.05.
El propósito de la siguiente actividad es darte una práctica guiada en la expresión de información en términos de probabilidades condicionales, y en el uso de la Regla General de Multiplicación.
Aprende haciendo: Probabilidad condicional y la regla general de multiplicación
Resumimos
Esta sección le introdujo los conceptos fundamentales de eventos independientes y probabilidad condicional, la probabilidad de un evento dado que otro evento ha ocurrido.
Vimos que a veces el conocimiento de que ha ocurrido otro evento no tiene impacto en la probabilidad (cuando los dos eventos son independientes), y a veces lo hace (cuando los dos eventos no son independientes).
Además discutimos la idea de independencia y discutimos diferentes formas de verificar si dos eventos son independientes o no.
Comprender el concepto de probabilidad condicional también nos permitió introducir nuestra regla de probabilidad final, la Regla General de Multiplicación.
La Regla General de Multiplicación nos dice cómo encontrar P (A y B) cuando A y B no son necesariamente independientes.

