Unidad 4A: Introducción a la Inferencia Estadística
- Última actualización
- Guardar como PDF
- Page ID
- 151203
CO-1: Describir los roles que la bioestadística desempeña en la disciplina de la salud pública.
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Reseña: Estamos a punto de entrar en el componente de inferencia del curso y es un buen momento para estar seguros de entender las ideas básicas presentadas respecto al análisis exploratorio de datos.
Video
Video: Unidad 4A: Introducción a la Inferencia Estadística (15:45)
Recordemos nuevamente el Big Picture, el proceso de cuatro pasos que engloba la estadística: producción de datos, análisis exploratorio de datos, probabilidad e inferencia.
Estamos a punto de iniciar la cuarta y última unidad de este curso, donde nos basamos en principios aprendidos en las otras unidades (Análisis Exploratorio de Datos, Producción de Datos y Probabilidad) para lograr lo que ha sido nuestro objetivo final a lo largo de todo el tiempo: usar una muestra para inferir (o sacar conclusiones) sobre la población de la que se extrajo.
Como verás en la introducción, la forma específica de inferencia requerida depende del tipo de variables involucradas —ya sea una sola variable categórica o cuantitativa, o bien una combinación de dos variables cuya relación es de interés.
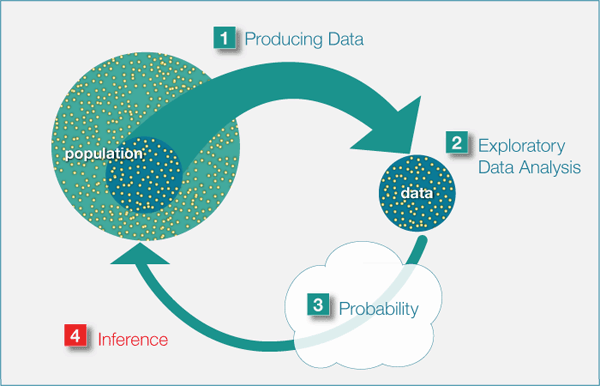
Introducción
Objetivos de aprendizaje
LO 6.23: Explicar cómo los conceptos cubiertos en las Unidades 1 — 3 proporcionan la base para la inferencia estadística.
Estamos a punto de iniciar la cuarta y última parte de este curso —inferencia estadística—, donde sacamos conclusiones sobre una población a partir de los datos obtenidos de una muestra elegida de la misma.
El propósito de esta introducción es revisar cómo llegamos hasta aquí y cómo encajan las unidades anteriores para permitirnos hacer inferencias confiables. También, presentaremos las diversas formas de inferencia estadística que se discutirán en esta dependencia, y daremos un esquema general de cómo se organiza esta dependencia.
En la unidad de Análisis Exploratorio de Datos aprendimos a mostrar y resumir los datos que se obtuvieron de una muestra. Independientemente de si teníamos una variable y examinamos su distribución, o si teníamos dos variables y examinamos la relación entre ellas, siempre se entendió que estos resúmenes se aplicaban únicamente a los datos en cuestión; no intentamos hacer afirmaciones sobre la población más grande de donde se obtuvieron los datos.
Tales generalizaciones fueron, sin embargo, un objetivo a largo plazo desde el comienzo mismo del curso. Por esta razón, en la unidad de Producción de Datos, nos encargamos de establecer principios de muestreo y diseño de estudios que serían esenciales para afirmar que, en cierta medida, lo que es cierto para la muestra también debería ser cierto para la población mayor de la que se originó la muestra.
Estos principios deben tenerse en cuenta a lo largo de esta unidad sobre la inferencia estadística, ya que los resultados que obtendremos no se mantendrán si hubo sesgo en el proceso de muestreo, o fallas en el diseño del estudio bajo el cual se midieron los valores de las variables.
Quizás el principio más importante que se destacó en la unidad Producing Data fue el de aleatorización. La aleatorización es esencial, no sólo porque evita sesgos, sino también porque nos permite apoyarnos en las leyes de la probabilidad, que es el estudio científico del comportamiento aleatorio.
En la unidad Probabilidad se establecieron leyes básicas para el comportamiento de variables aleatorias. Finalmente, nos enfocamos en dos variables aleatorias de particular relevancia: la media muestral (x-bar) y la proporción muestral (p-hat), y la última sección de la unidad Probabilidad se dedicó a explorar sus distribuciones muestrales.
Aprendimos lo que la teoría de probabilidad nos dice esperar de los valores de la media muestral y la proporción muestral, dado que se conocen los parámetros poblacionales correspondientes —la media poblacional (mu, μ) y la proporción poblacional (p )—.
Como mencionamos en esa sección, el valor de tales resultados es más teórico que práctico, ya que en situaciones de la vida real rara vez sabemos lo que es cierto para toda la población. Todo lo que sabemos es lo que vemos en la muestra, y queremos usar esta información para decir algo concreto sobre la población más grande.
La teoría de la probabilidad ha sentado las bases para lograr esto: aprender qué esperar del valor de la media de la muestra, dado que la media poblacional toma cierto valor, nos enseña (como pronto aprenderemos) qué esperar del valor de la media de la población desconocida, dado que un valor particular de la media muestral tiene se ha observado.
De igual manera, ya que hemos establecido cómo se comporta la proporción muestral en relación con la proporción poblacional, ahora podremos darle la vuelta y decir algo sobre el valor de la proporción poblacional, con base en una proporción muestral observada. Este proceso —inferir algo sobre la población con base en lo que se mide en la muestra— se llama (como ustedes saben) inferencia estadística.
Tipos de inferencia
Objetivos de aprendizaje
LO: 1.9 Distinguir entre situaciones usando una estimación puntual, una estimación de intervalo o una prueba de hipótesis.
Introduciremos tres formas de inferencia estadística en esta unidad, cada una de las cuales representa una manera diferente de utilizar la información obtenida en la muestra para sacar conclusiones sobre la población. Estas formas son:
- Estimación de puntos
- Estimación de Intervalos
- Prueba de Hipótesis
Obviamente, cada una de estas formas de inferencia se discutirá extensamente en esta sección, pero sería útil obtener al menos un sentido intuitivo de la naturaleza de cada una de estas formas de inferencia, y la diferencia entre ellas en cuanto a los tipos de conclusiones que sacan sobre la población con base en las resultados de la muestra.
Estimación de puntos
En la estimación puntual, estimamos un parámetro desconocido utilizando un solo número que se calcula a partir de los datos de la muestra.
EJEMPLO:
Con base en los resultados de la muestra, estimamos que p, la proporción de todos los adultos estadounidenses que están a favor de un control más estricto de las armas de fuego, es de 0.6.
Estimación de Intervalos
En la estimación de intervalos, estimamos un parámetro desconocido usando un intervalo de valores que probablemente contenga el valor verdadero de ese parámetro (y declaramos cuán seguros estamos de que este intervalo efectivamente captura el valor verdadero del parámetro).
EJEMPLO:
Con base en los resultados de la muestra, estamos 95% seguros de que p, la proporción de todos los adultos estadounidenses que están a favor de un control de armas más estricto, está entre 0.57 y 0.63.
Prueba de Hipótesis
En las pruebas de hipótesis, comenzamos con una afirmación sobre la población (llamaremos la hipótesis nula), y verificamos si los datos obtenidos de la muestra proporcionan o no evidencia CONTRA esta afirmación.
EJEMPLO:
Se afirmó que entre todos los adultos estadunidenses, cerca de la mitad están a favor de un control de armas más estricto y cerca de la mitad están en contra de ello. En una encuesta reciente de una muestra aleatoria de 1,200 adultos estadounidenses, el 60% estuvo a favor de un control de armas más estricto. Estos datos, por lo tanto, aportan algunas pruebas contra la demanda.
Pronto determinaremos la probabilidad de que podríamos haber visto tal resultado (60% a favor) o más extremo SI de hecho la verdadera proporción de todos los adultos estadounidenses que favorecen un control de armas más estricto es en realidad 0.5 (el valor en la reclamación que los datos intentan refutar).
EJEMPLO:
Se afirma que entre los conductores de 18 a 23 años de edad (nuestra población) no existe relación entre conducir ebrio y género.
Una encuesta en carretera recopiló datos de una muestra aleatoria de 5 mil conductores y registró su género y si estaban borrachos.
Los datos recopilados mostraron aproximadamente el mismo porcentaje de conductores ebrios entre hombres y entre mujeres. Estos datos, por lo tanto, no nos dan ninguna razón para rechazar la afirmación de que no existe relación entre conducir ebrio y género.
¿Obtuve esto? : Tipos de inferencia
En términos de organización, la unidad de Inferencia consta de dos partes principales: Inferencia para Una Variable e Inferencia para Relaciones entre Dos Variables. La organización de cada una de estas partes se discutirá más a medida que avancemos a través de la dependencia.
Inferencia para una variable
Los dos temas siguientes en la unidad de inferencia tratarán de la inferencia para una variable. Recordemos que en la unidad de Análisis Exploratorio de Datos (EDA), cuando aprendimos a resumir los datos obtenidos de una variable donde aprendimos a examinar distribuciones, distinguimos entre dos casos; datos categóricos y datos cuantitativos.
Haremos una distinción similar aquí en la unidad de inferencia. En la unidad EDA, el tipo de variable determinó las pantallas y medidas numéricas que utilizamos para resumir los datos. En Inferencia, el tipo de variable de interés (categórica o cuantitativa) determinará qué parámetro poblacional es de interés.
- Cuando la variable de interés es categórica, el parámetro poblacional sobre el que inferiremos es la proporción poblacional (p) asociada a esa variable. Por ejemplo, si estamos interesados en estudiar opiniones sobre la pena de muerte entre adultos estadounidenses, y así nuestra variable de interés es “la pena de muerte (a favor/en contra)”, elegiremos una muestra de adultos estadounidenses y usaremos los datos recopilados para hacer una inferencia sobre p, la proporción de adultos estadounidenses que apoyan la pena de muerte.
- Cuando la variable de interés es cuantitativa, el parámetro poblacional sobre el que inferimos es la media poblacional (mu, µ) asociada a esa variable. Por ejemplo, si nos interesa estudiar los salarios anuales en la población de maestros en un determinado estado, elegiremos una muestra de esa población y utilizaremos los datos salariales recopilados para hacer una inferencia sobre µ, el salario medio anual de todos los maestros de ese estado.
Los siguientes esquemas describen algunos de los puntos importantes sobre el proceso de la estadística inferencial, así como comparar y contrastar cómo investigadores y estadísticos abordan este proceso.
Esquema del Proceso de Inferencia
Aquí hay otra reafirmación del panorama general de la inferencia estadística en lo que respecta a los dos ejemplos simples que discutiremos primero.
- Se toma una muestra aleatoria simple de una población de interés.
- Para estimar un parámetro poblacional, se calcula un estadístico a partir de la muestra. Por ejemplo:
Media de la muestra (barra x)
Proporción de muestra (p-hat)
- Luego aprendemos sobre la DISTRIBUCIÓN de esta estadística en muestreos repetidos (teóricamente). ¡Ahora sabemos que estas se llaman distribuciones de muestreo!
- Usando ESTA distribución muestral podemos hacer inferencias sobre nuestro parámetro poblacional con base en nuestro estadístico muestral.
Es este último paso de inferencia estadística lo que nos interesa discutir ahora.
Pasos Aplicados (¿Qué hacen los investigadores?)
Un problema para los estudiantes es que el proceso teórico de inferencia estadística es sólo una pequeña parte de los pasos aplicados en un proyecto de investigación. Anteriormente, en nuestra discusión sobre el papel de la bioestadística, definimos estos pasos para ser:
- Planificación/diseño de estudio
- Recogida de datos
- Análisis de datos
- Presentación
- Interpretación
Se puede ver que:
- Tanto el análisis exploratorio de datos como los métodos inferenciales entrarán en la categoría de “Análisis de datos” en nuestra lista anterior.
- La probabilidad se oculta en los pasos aplicados en forma de planes de muestreo probabilístico, estimación de probabilidades deseadas y distribuciones de muestreo.
Entre los investigadores, las siguientes representan algunas de las preguntas importantes a abordar al realizar un estudio.
- ¿Cuál es la población de interés?
- ¿Cuál es la pregunta o problema estadístico?
- ¿Cómo muestrear para abordar mejor la pregunta dados los recursos disponibles?
- ¿Cómo analizar los datos?
- ¿Cómo reportar los resultados?
DESPUÉS de que sepas lo que vas a hacer, ¡entonces puedes comenzar a recopilar datos!
Pasos teóricos (¿Qué hacen los estadísticos?)
Los estadísticos, por otro lado, necesitan hacer preguntas como estas:
- ¿Qué supuestos se pueden hacer razonablemente sobre la población?
- ¿Qué parámetro (s) en la población necesitamos estimar para abordar la pregunta de investigación?
- ¿Qué estadística (es) de nuestros datos de muestra se pueden utilizar para estimar el parámetro o parámetros desconocidos?
- ¿Cómo se comporta cada estadística?
- ¿Es imparcial?
- ¿Qué tan variable será para el tamaño de muestra planificado?
- ¿Cuál es la distribución de esta estadística? (Distribución de Muestreo)
Entonces, veremos que podemos usar la distribución de muestreo de un estadístico para:
- Proporcionar estimaciones del intervalo de confianza para el parámetro correspondiente.
- Realizar pruebas de hipótesis sobre el parámetro correspondiente.
Error estándar de una estadística
Objetivos de aprendizaje
LO: 1.10: Definir el error estándar de un estadístico con precisión y relacionarlo con el concepto de la distribución muestral de una estadística.
En nuestra discusión sobre las distribuciones de muestreo, discutimos la variabilidad de la estadística muestral; aquí hay una revisión rápida de este concepto general y una definición formal del error estándar de una estadística.
- Todos los estadísticos calculados a partir de muestras son variables aleatorias.
- La distribución de un estadístico (a partir de una muestra de un tamaño de muestra dado) se denomina distribución muestral del estadístico.
- La desviación estándar de la distribución muestral de un estadístico particular se denomina error estándar del estadístico y mide la variabilidad del estadístico para un tamaño de muestra particular.
El error estándar de un estadístico es la desviación estándar de la distribución muestral de ese estadístico, donde la distribución de muestreo se define como la distribución de un estadístico particular en muestreo repetido.
- El error estándar es una medida extremadamente común de la variabilidad de un estadístico muestral.
EJEMPLO:
En nuestra discusión sobre las distribuciones de muestreo, observamos una situación que involucra una muestra aleatoria de 100 estudiantes tomados de la población de todos los estudiantes de medio tiempo en Estados Unidos, para lo cual la proporción general de mujeres es de 0.6. Aquí tenemos una variable categórica de interés, género.
Se determinó que la distribución de todos los valores posibles de p-hat (que podríamos obtener para muestras aleatorias simples repetidas de este tamaño de esta población) tiene media p = 0.6 y desviación estándar
\(\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}=\sqrt{\dfrac{0.6(1-0.6)}{100}}=0.05\)
que ahora hemos aprendido se llama más formalmente el error estándar de p-hat. En este caso, el verdadero error estándar de p-hat será 0.05.
También mostramos cómo podemos usar esta información junto con información sobre el centro (valor medio o esperado) para calcular probabilidades asociadas a valores particulares de p-hat. Por ejemplo, ¿cuál es la probabilidad de que la proporción muestral p-hat sea menor o igual a 0.56? Después de verificar que los requisitos de tamaño de muestra son razonables, podemos usar una distribución normal para aproximar
\(P(\hat{p} \leq 0.56)=P\left(Z \leq \dfrac{0.56-0.6}{0.05}\right)=P(Z \leq-0.80)=0.2119\)
EJEMPLO:
De igual manera, para una variable cuantitativa, observamos un ejemplo del tamaño del hogar en Estados Unidos que tiene una media de 2.6 personas y una desviación estándar de 1.4 personas.
Si consideramos tomar una muestra aleatoria simple de 100 hogares, encontramos que la distribución de medias muestrales (barra x) es aproximadamente normal para un tamaño de muestra grande como n = 100.
La distribución muestral de la barra x tiene una media que es la misma que la media poblacional, 2.6, y su desviación estándar es la desviación estándar poblacional dividida por la raíz cuadrada del tamaño de la muestra:
\(\dfrac{\sigma}{\sqrt{n}}=\dfrac{1.4}{\sqrt{100}}=0.14\)
Nuevamente, esta desviación estándar de la distribución muestral de la barra x se denomina más comúnmente el error estándar de la barra x, en este caso 0.14. Y podemos usar esta información (el centro y propagación de la distribución muestral) para encontrar probabilidades que involucren valores particulares de x-bar.
\(P(\bar{x}>3)=P\left(Z>\dfrac{3-2.6}{\dfrac{1.4}{\sqrt{100}}}\right)=P(Z>2.86)=0.0021\)

