Prueba de Hipótesis

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Objetivos de aprendizaje

LO 6.27: Explique qué es el valor p y cómo se utiliza para sacar conclusiones.

Video

Video: Prueba de Hipótesis (8:43)

Introducción

Estamos en medio de la parte del curso que tiene que ver con la inferencia para una variable.

Hasta el momento, hablamos de estimación de puntos y aprendimos cómo la estimación de intervalos la potencia cuantificando la magnitud del error de estimación (con cierto nivel de confianza) en forma de margen de error. El resultado es el intervalo de confianza, un intervalo que, con cierta confianza, creemos que captura el parámetro desconocido.

Ahora estamos pasando al otro tipo de inferencia, la prueba de hipótesis. Decimos que la prueba de hipótesis es “del otro tipo” porque, a diferencia de los métodos inferenciales que presentamos hasta ahora, donde el objetivo era estimar el parámetro desconocido, la idea, la lógica y el objetivo de las pruebas de hipótesis son bastante diferentes.

En las dos primeras partes de esta sección discutiremos la idea detrás de las pruebas de hipótesis, explicaremos cómo funciona e introduciremos nueva terminología que surge en esta forma de inferencia. Las dos partes finales serán más específicas y discutirán pruebas de hipótesis para la proporción poblacional (p) y la media poblacional (μ, mu).

Si este es tu primer curso de estadística, necesitarás dedicar un tiempo considerable a este tema ya que hay muchas ideas nuevas. Muchos estudiantes encuentran este proceso y su lógica difícil de entender al principio.

En esta sección, utilizaremos la prueba de hipótesis para una proporción poblacional para motivar nuestra comprensión del proceso. Realizaremos estas pruebas manualmente. Para todos los futuros procedimientos de prueba de hipótesis, incluyendo problemas que involucren medios, utilizaremos software para obtener los resultados y enfocarnos en interpretarlos en el contexto de nuestro escenario.

Idea general y lógica de pruebas de hipótesis

El propósito de esta sección es construir gradualmente su comprensión sobre cómo funcionan las pruebas de hipótesis estadísticas. Comenzamos explicando la lógica general detrás del proceso de prueba de hipótesis. Una vez que estemos seguros de que entiendes esta lógica, agregaremos algunos detalles y terminología más.

Para iniciar nuestra discusión sobre la idea detrás de las pruebas de hipótesis estadísticas, considere el siguiente ejemplo:

EJEMPLO:

Un caso de sospecha de trampa en un examen se presenta ante el comité disciplinario de una determinada universidad.

Hay dos pretensiones opuestas en este caso:

• El reclamo del alumno: No hice trampa en el examen.
• El reclamo del instructor: El alumno hizo trampa en el examen.

Adhiriéndose al principio de “inocente hasta que se demuestre su culpabilidad”, el comité pide al instructor pruebas que respalden su afirmación. El instructor explica que el examen tuvo dos versiones, y muestra a los miembros del comité que en tres preguntas separadas del examen, el alumno utilizó en su solución los números que se dieron en la otra versión del examen.

Todos los miembros del comité coinciden en que sería extremadamente improbable obtener pruebas así si la afirmación del estudiante de no hacer trampa hubiera sido cierta. Es decir, todos los miembros del comité coinciden en que el instructor presentó pruebas lo suficientemente fuertes como para rechazar la afirmación del estudiante, y concluyen que el estudiante sí engañó en el examen.

¿Qué tiene que ver este ejemplo con las estadísticas?

Si bien es cierto que esta historia parece no relacionada con la estadística, captura todos los elementos de las pruebas de hipótesis y la lógica detrás de ella. Antes de seguir leyendo para entender por qué, sería útil volver a leer el ejemplo. Por favor, hágalo ahora.

Las pruebas de hipótesis estadísticas se definen como:

• Evaluar las pruebas aportadas por los datos frente a la demanda nula (la demanda que se debe suponer verdadera a menos que existan suficientes pruebas para rechazarla).

Así es como funciona el proceso de pruebas de hipótesis estadísticas:

1. Tenemos dos afirmaciones sobre lo que está pasando en la población. Llamémoslos reclamo 1 (este será el reclamo nulo o hipótesis) y reclamo 2 (esta será la alternativa). Al igual que la historia anterior, donde el reclamo del estudiante es impugnado por el reclamo del instructor, el reclamo nulo 1 es impugnado por el reclamo alternativo 2. (Para nosotros, estas afirmaciones suelen ser sobre el valor del parámetro o parámetros de población o sobre la existencia o inexistencia de una relación entre dos variables en la población).

   ---

2. Elegimos una muestra, recolectamos datos relevantes y los resumimos (esto es similar al instructor que recoge evidencia del examen del alumno). Para las pruebas estadísticas, este paso también implicará verificar cualquier condición o suposición.

   ---

3. Descubrimos qué tan probable es observar datos como los datos que obtuvimos, si la reivindicación 1 es cierta. (Obsérvese que la redacción “qué tan probable...” implica que este paso requiere algún tipo de cálculo de probabilidad). En la historia, los miembros del comité evaluaron qué tan probable es observar pruebas como las que proporcionó el instructor, si la afirmación del estudiante de no hacer trampa hubiera sido cierta.

   ---

4. En base a lo que encontramos en el paso anterior, tomamos nuestra decisión:
   • Si, después de asumir que la reclamación 1 es cierta, encontramos que sería extremadamente improbable observar datos tan fuertes como los nuestros o más fuertes a favor de la reclamación 2, entonces tenemos pruebas contundentes contra la reclamación 1, y la rechazamos a favor del reclamo 2. Posteriormente veremos que esto corresponde a un pequeño valor p.
   • Si, después de asumir que la reivindicación 1 es cierta, encontramos que observar datos tan fuertes como los nuestros o más fuertes a favor del reclamo 2 NO ES MUY IMPOSIBLE, entonces no tenemos pruebas suficientes contra la reclamación 1, y por lo tanto no podemos rechazarla a favor del reclamo 2. Posteriormente veremos que esto corresponde a un valor p que no es pequeño.

En nuestra historia, el comité decidió que sería extremadamente improbable encontrar las pruebas que el instructor proporcionó si la afirmación del estudiante de no hacer trampa hubiera sido cierta. Es decir, los integrantes sintieron que es extremadamente improbable que sea solo una coincidencia (azar azar) que el alumno utilizó los números de la otra versión del examen en tres problemas separados. Por lo tanto, los integrantes del comité decidieron rechazar la afirmación del alumno y concluyeron que el alumno, efectivamente, había engañado en el examen. (¿No concluiría lo mismo?)

Ojalá este ejemplo te haya ayudado a entender la lógica detrás de las pruebas de hipótesis.

Applet interactivo: razonamiento de una prueba estadística

Para fortalecer su comprensión del proceso de prueba de hipótesis y la lógica detrás del mismo, veamos tres ejemplos estadísticos.

EJEMPLO:

Un estudio reciente estimó que el 20% de todos los estudiantes universitarios en Estados Unidos fuman. El jefe de Servicios de Salud de la Universidad Goodheart (GU) sospecha que la proporción de fumadores puede ser menor en GU. Con la esperanza de confirmar su afirmación, la jefa de Servicios de Salud elige una muestra aleatoria de 400 estudiantes de Goodheart, y encuentra que 70 de ellos son fumadores.

Analicemos este ejemplo usando los 4 pasos descritos anteriormente:

1. Afirmando las pretensiones: Aquí hay dos reclamaciones:
   • reclamo 1: La proporción de fumadores en Goodheart es de 0.20.
   • reclamo 2: La proporción de fumadores en Goodheart es menor a 0.20.

   La reivindicación 1 básicamente dice “no pasa nada especial en la Universidad Goodheart; la proporción de fumadores no es diferente de la proporción en todo el país”. Esta afirmación es impugnada por el jefe de Servicios de Salud, quien sospecha que la proporción de fumadores en Goodheart es menor.

   ---

2. Elegir una muestra y recolectar datos: Se eligió una muestra de n = 400, y resumiendo los datos reveló que la proporción muestral de fumadores es p -hat = 70/400 = 0.175.Si bien es cierto que 0.175 es menor que 0.20, no está claro si esta es evidencia suficientemente fuerte contra demanda 1. Debemos dar cuenta de la variación del muestreo.

   ---

3. Valoración de pruebas: Para evaluar si los datos aportan pruebas suficientemente sólidas contra la reclamación 1, debemos preguntarnos: ¿Qué tan sorprendente es obtener una proporción muestral tan baja como p -hat = 0.175 (o inferior), asumiendo que la reivindicación 1 es cierta? Es decir, necesitamos encontrar cuán probable es que en una muestra aleatoria de tamaño n = 400 tomada de una población donde la proporción de fumadores es p = 0.20 obtengamos una proporción muestral tan baja como p -hat = 0.175 (o menor) .Resulta que la probabilidad que obtendremos una proporción muestral tan baja como p -hat = 0.175 (o menor) en tal muestra es aproximadamente 0.106 (no te preocupes por cómo se calculó esto en este punto — sin embargo, si lo piensas ojalá puedas ver que la clave es la distribución muestral de p -sombrero).

   ---

4. Conclusión: Bueno, encontramos que si la reivindicación 1 fuera cierta existe una probabilidad de 0.106 de observar datos como los observados o más extremos. Ahora hay que decidir... ¿Cree que una probabilidad de 0.106 hace que nuestros datos sean lo suficientemente raros (lo suficientemente sorprendentes) bajo la reivindicación 1 para que el hecho de que sí lo observáramos sea evidencia suficiente para rechazar la reivindicación 1? O cree que una probabilidad de 0.106 significa que datos como los que observamos no son muy probables cuando la reivindicación 1 es cierta, pero no son lo suficientemente improbables como para concluir que obtener dichos datos es evidencia suficiente para rechazar la reivindicación 1. Básicamente, esta es tu decisión. No obstante, sería bueno tener algún tipo de pauta sobre lo que generalmente se considera suficientemente sorprendente.

EJEMPLO:

Se supone que cierto medicamento recetado para la alergia contiene un promedio de 245 partes por millón (ppm) de un determinado químico. Si la concentración es superior a 245 ppm, el medicamento probablemente causará efectos secundarios desagradables, y si la concentración está por debajo de 245 ppm, el medicamento puede ser ineficaz. El fabricante quiere verificar si la concentración media en un envío grande es la requerida 245 ppm o no. Para ello, se prueba una muestra aleatoria de 64 porciones del envío grande, y se encuentra que la concentración media de la muestra es de 250 ppm con una desviación estándar de la muestra de 12 ppm.

1. Afirmar las reclamaciones:
   • Reclamación 1: La concentración media en el envío es la requerida 245 ppm.
   • Reclamación 2: La concentración media en el envío no es la requerida 245 ppm.

   Tenga en cuenta que nuevamente, la reivindicación 1 básicamente dice: “No hay nada inusual en este envío, la concentración media es la requerida 245 ppm”. Esta afirmación es impugnada por el fabricante, quien quiere comprobar si ese es, efectivamente, el caso o no.

   ---

2. Elegir una muestra y recolectar datos: Se elige una muestra de n = 64 porciones y después de resumir los datos se encuentra que la concentración media de la muestra es x-bar = 250 y la desviación estándar de la muestra es s = 12.Es el hecho de que x-bar = 250 es diferente de 245 evidencia lo suficientemente fuerte como para rechazar reivindicación 1 y concluir que la concentración media en todo el envío no es la requerida 245? Es decir, ¿los datos proporcionan pruebas suficientemente sólidas como para rechazar la reclamación 1?

   ---

3. Evaluando la evidencia: Para evaluar si los datos proporcionan evidencia suficientemente sólida contra la reivindicación 1, necesitamos hacernos la siguiente pregunta: Si la concentración media en todo el envío fuera realmente la requerida 245 ppm (es decir, si la reivindicación 1 fuera cierta), qué tan sorprendente sería observar una muestra de 64 porciones donde la concentración media de la muestra está apagada en 5 ppm o más (como hicimos nosotros)? Resulta que sería extremadamente improbable obtener tal resultado si la concentración media fuera realmente la requerida 245. Solo hay una probabilidad de 0.0007 (es decir, 7 de cada 10,000) de que eso suceda. (No se preocupe por cómo se calculó esto en este punto, pero nuevamente, la clave será la distribución del muestreo).

   ---

4. Conclusiones: Aquí, es bastante claro que una muestra como la que observamos o más extrema es MUY rara (o extremadamente improbable) si la concentración media en el envío fuera realmente la requerida 245 ppm. El hecho de que sí observáramos tal muestra, por lo tanto, aporta pruebas contundentes contra la reivindicación 1, por lo que la rechazamos y concluimos con muy pocas dudas que la concentración media en el envío no es la requerida 245 ppm.

¿Crees que lo estás consiguiendo? Asegurémonos, y miremos otro ejemplo.

EJEMPLO:

¿Existe relación entre género y puntuaciones combinadas (Math + Verbal) en el examen SAT?

A raíz de un reporte en la página web de College Board, que mostró que en 2003, los varones obtuvieron calificaciones generalmente más altas que las mujeres en el examen SAT, una investigadora educativa quiso comprobar si este era también el caso en su distrito escolar. La investigadora eligió muestras aleatorias de 150 varones y 150 mujeres de su distrito escolar, recolectó datos sobre su desempeño SAT y encontró lo siguiente:

Hembras		Machos
n media desviación estándar 150 1010 206		n media desviación estándar 150 1025 212

Nuevamente, veamos cómo funciona el proceso de prueba de hipótesis para este ejemplo:

1. Afirmar las reclamaciones:
   • Reclamación 1: El desempeño en el SAT no está relacionado con el género (hombres y mujeres puntúan lo mismo).
   • Reclamación 2: El desempeño en el SAT está relacionado con el género — los varones obtienen mayor puntuación.

   Tenga en cuenta que nuevamente, la reivindicación 1 básicamente dice: “No pasa nada entre las variables SAT y género”. La Reclamación 2 representa lo que el investigador quiere verificar, o los sospechosos podrían ser realmente el caso.

   ---

2. Elección de una muestra y recolección de datos: Los datos fueron recolectados y resumidos como se indicó anteriormente. ¿Es el hecho de que la puntuación media muestral de varones (1,025) sea mayor que la puntuación media muestral de las mujeres (1,010) por 15 puntos lo suficientemente fuerte como para rechazar la reivindicación 1 y concluir que en este distrito escolar de este investigador, los varones obtienen puntajes más altos en el SAT que en las mujeres?

   ---

3. Evaluación de evidencias: Para evaluar si los datos proporcionan evidencia suficientemente sólida contra la reclamación 1, debemos preguntarnos: Si los puntajes SAT de hecho no están relacionados con el género (la reivindicación 1 es cierta), qué tan probable es obtener datos como los datos que observamos, en los que la diferencia entre los hombres” promedio y el puntaje promedio de las mujeres es tan alto como 15 puntos o superior? Resulta que la probabilidad de observar tal resultado muestral si la puntuación SAT no está relacionada con el género es de aproximadamente 0.29 (Nuevamente, no te preocupes por cómo se calculó esto en este punto).

   ---

4. Conclusión: Aquí tenemos un ejemplo donde observar una muestra como la que observamos o más extrema definitivamente no es sorprendente (aproximadamente 30% de probabilidad) si la reivindicación 1 fuera cierta (es decir, si efectivamente no hay diferencia en las puntuaciones SAT entre hombres y mujeres). Por lo tanto, concluimos que nuestros datos no aportan pruebas suficientes para rechazar la reclamación 1.

Comentario:

• Regrese y lea las secciones de conclusión de los tres ejemplos, y preste atención a la redacción. Tenga en cuenta que hay dos tipos de conclusiones:
  • “Los datos aportan pruebas suficientes para rechazar la reclamación 1 y aceptar la reclamación 2”; o
  • “Los datos no aportan pruebas suficientes para rechazar la reclamación 1.”

En particular, tenga en cuenta que en el segundo tipo de conclusión no dijimos: “Acepto la reclamación 1”, sino sólo “no tengo pruebas suficientes para rechazar la reclamación 1”. Volveremos a este tema más adelante, pero este es un buen lugar para hacerte consciente de esta sutil diferencia.

Ojalá a estas alturas, entiendas la lógica detrás del proceso de prueba de hipótesis estadísticas. Aquí hay un resumen:

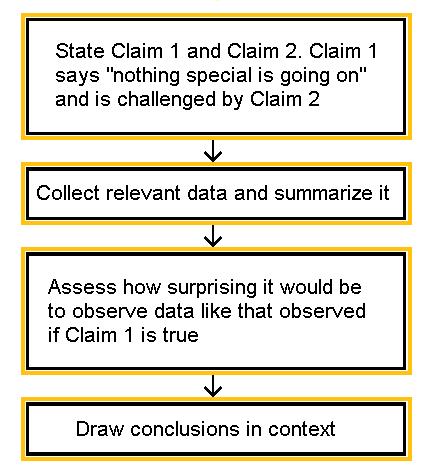
Aprender haciendo: Lógica de las pruebas de hipótesis

¿Conseguí esto? : Lógica de las pruebas de hipótesis

Pasos en las pruebas de hipótesis

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Objetivos de aprendizaje

LO 6.27: Explique qué es el valor p y cómo se utiliza para sacar conclusiones.

Video

Video: Pasos en las pruebas de hipótesis (16:02)

Ahora que entendemos la idea general de cómo funcionan las pruebas de hipótesis estadísticas, volvamos a cada uno de los pasos y profundicemos un poco más, obteniendo más detalles y aprendiendo algo de terminología.

Prueba de Hipótesis Paso 1: Indicar las Hipótesis

En los tres ejemplos, nuestro objetivo es decidir entre dos puntos de vista opuestos, Reclamación 1 y Reclamación 2. En las pruebas de hipótesis, la reivindicación 1 se llama hipótesis nula (denotada “Ho “), y la reivindicación 2 juega el papel de la hipótesis alternativa (denotada “Ha “). Como vimos en los tres ejemplos, la hipótesis nula sugiere que no está pasando nada especial; es decir, no hay cambio con respecto al status quo, ninguna diferencia con el estado de cosas tradicional, ninguna relación. En contraste, la hipótesis alternativa no está de acuerdo con esto, afirmando que algo está pasando, o hay un cambio con respecto al status quo, o hay una diferencia con el estado de cosas tradicional. La hipótesis alternativa, Ha, suele representar lo que queremos comprobar o lo que sospechamos que realmente está sucediendo.

Volvamos a nuestros tres ejemplos y apliquemos la nueva notación:

En el ejemplo 1:

• Ho: La proporción de fumadores en GU es de 0.20.
• Ha: La proporción de fumadores en GU es menor a 0.20.

En el ejemplo 2:

• Ho: La concentración media en el envío es la requerida 245 ppm.
• Ha: La concentración media en el envío no es la requerida 245 ppm.

En el ejemplo 3:

• Ho: El desempeño en el SAT no está relacionado con el género (hombres y mujeres puntúan lo mismo).
• Ja: El desempeño en el SAT está relacionado con el género — los varones puntúan más alto.

Aprender haciendo: Indicar las hipótesis

¿Conseguí esto? : Exponer las Hipótesis

Prueba de hipótesis Paso 2: Recopilar datos, verificar condiciones y resumir datos

Este paso es bastante obvio. De esto se trata la inferencia. Se observan los datos muestreados para sacar conclusiones sobre toda la población. En el caso de las pruebas de hipótesis, con base en los datos, se sacan conclusiones sobre si hay o no pruebas suficientes para rechazar a Ho.

Hay, sin embargo, un detalle que nos gustaría agregar aquí. En este paso recogemos datos y los resumimos. Regresa y mira el segundo paso en nuestros tres ejemplos. Tenga en cuenta que para resumir los datos se utilizaron estadísticas de muestra simples como la proporción muestral (p -hat), la media de la muestra (barra x) y la desviación estándar de la muestra.

En la práctica, vas un paso más allá y usas estas estadísticas de muestra para resumir los datos con lo que se llama una estadística de prueba. No vamos a entrar en ningún detalle en este momento, pero discutiremos las estadísticas de las pruebas cuando pasemos por las pruebas específicas.

Este paso también implicará verificar cualquier condición o suposición requerida para usar la prueba.

Prueba de hipótesis Paso 3: Evaluar la evidencia

Como vimos, este es el paso en el que calculamos qué tan probable es que obtenga datos como los observados (o más extremos) cuando Ho es cierto. En cierto sentido, este es el corazón del proceso, ya que sacamos nuestras conclusiones con base en esta probabilidad.

• Si esta probabilidad es muy pequeña (ver ejemplo 2), entonces eso significa que sería muy sorprendente obtener datos como los observados (o más extremos) si Ho fuera cierto. El hecho de que sí observáramos tales datos es, por lo tanto, evidencia en contra de Ho, y debemos rechazarla.
• Por otro lado, si esta probabilidad no es muy pequeña (ver ejemplo 3) esto significa que observar datos como los observados (o más extremos) no es muy sorprendente si Ho fuera cierto. El hecho de que hayamos observado tales datos no aporta pruebas contra Ho. Esta probabilidad crucial, por lo tanto, tiene un nombre especial. Se llama el valor p de la prueba.

En nuestros tres ejemplos, se le dieron los valores p (y se le aseguró que aún no tenía que preocuparse por cómo se derivaron estos):

• Ejemplo 1: valor p = 0.106
• Ejemplo 2: valor p = 0.0007
• Ejemplo 3: valor p = 0.29

Obviamente, cuanto menor es el valor p, más sorprendente es obtener datos como el nuestro (o más extremos) cuando Ho es cierto, y por lo tanto, más fuerte es la evidencia que proporcionan los datos contra Ho.

Al observar los tres valores p de nuestros tres ejemplos, vemos que los datos que observamos en el ejemplo 2 proporcionan la evidencia más fuerte contra la hipótesis nula, seguido del ejemplo 1, mientras que los datos del ejemplo 3 proporcionan la menor evidencia contra Ho.

Comentario:

• En este momento no entraremos en detalles específicos sobre los cálculos del valor p, sino que solo mencionaremos que dado que el valor p es la probabilidad de obtener datos como los observados (o más extremos) cuando Ho es cierto, tendría sentido que el cálculo del valor p se basara en el resumen de datos, que, como mencionamos, es el estadístico de prueba. En efecto, este es el caso. En la práctica, usaremos principalmente software para proporcionar el valor p para nosotros.

Prueba de hipótesis Paso 4: sacar conclusiones

Dado que nuestra conclusión estadística se basa en lo pequeño que es el valor p, o en otras palabras, cuán sorprendentes son nuestros datos cuando Ho es cierto, sería bueno tener algún tipo de pauta o corte que ayude a determinar qué tan pequeño debe ser el valor p, o cuán “raros” (improbables) deben ser nuestros datos cuando Ho es cierto, para nosotros para concluir que tenemos pruebas suficientes para rechazar a Ho.

Este límite existe, y por ser tan importante, tiene un nombre especial. Se llama el nivel de significancia de la prueba y generalmente se denota con la letra griega α (alfa). El nivel de significancia más utilizado es α (alfa) = 0.05 (o 5%). Esto significa que:

• si el valor p < α (alfa) (generalmente 0.05), entonces los datos que obtuvimos se consideran “raros (o sorprendentes) suficientes” bajo el supuesto de que Ho es cierto, y decimos que los datos proporcionan evidencia estadísticamente significativa contra Ho, por lo que rechazamos Ho y así aceptamos Ha.
• si el valor p > α (alfa) (generalmente 0.05), entonces nuestros datos no se consideran “lo suficientemente sorprendentes” bajo el supuesto de que Ho es cierto, y decimos que nuestros datos no proporcionan suficiente evidencia para rechazar Ho (o, de manera equivalente, que los datos no proporcionan suficiente evidencia para aceptar Ha).

Ahora que tenemos un corte para usar, aquí están las conclusiones apropiadas para cada uno de nuestros ejemplos basados en los valores p que nos dieron.

En el Ejemplo 1:

• Usando nuestro corte de 0.05, fallamos en rechazar a Ho.
• Conclusión: NO HAY evidencia suficiente de que la proporción de fumadores en GU sea inferior a 0.20
• Aún así debemos considerar: ¿La evidencia vista en los datos proporciona alguna evidencia práctica hacia nuestra hipótesis alternativa?

En el Ejemplo 2:

• Usando nuestro corte de 0.05, rechazamos Ho.
• Conclusión: Existe suficiente evidencia de que la concentración media en el envío no es la requerida 245 ppm.
• Aún así debemos considerar: ¿La evidencia vista en los datos proporciona alguna evidencia práctica hacia nuestra hipótesis alternativa?

En el Ejemplo 3:

• Usando nuestro corte de 0.05, fallamos en rechazar a Ho.
• Conclusión: NO HAY evidencia suficiente de que los machos puntúen más altos en promedio que las hembras en el SAT.
• Aún así debemos considerar: ¿La evidencia vista en los datos proporciona alguna evidencia práctica hacia nuestra hipótesis alternativa?

Observe que todas las conclusiones anteriores están escritas en términos de la hipótesis alternativa y se dan en el contexto de la situación. En ninguna situación hemos afirmado que la hipótesis nula es cierta. Tenga mucho cuidado con este y otros temas tratados en los siguientes comentarios.

Comentarios:

1. Si bien el nivel de significancia proporciona una buena pauta para sacar nuestras conclusiones, no debe tratarse como una verdad incontrovertible. Hay mucho espacio para la interpretación personal. ¿Y si tu valor p es 0.052? Quizás quieras apegarte a las reglas y decir “0.052 > 0.05 y por lo tanto no tengo pruebas suficientes para rechazar a Ho”, pero podrías decidir que 0.052 es lo suficientemente pequeño como para que creas que Ho debe ser rechazado. Cabe señalar que las revistas científicas sí consideran 0.05 como el punto de corte para el cual cualquier valor p por debajo del corte indica suficiente evidencia contra Ho, y cualquier valor p por encima de él, o incluso igual a él, indica que no hay suficiente evidencia contra Ho. Aunque un valor de p entre 0.05 y 0.10 a menudo se reporta como marginalmente estadísticamente significativo.

   ---

2. Es importante sacar sus conclusiones en contexto. Nunca es suficiente decir: “valor p =..., y por lo tanto tengo pruebas suficientes para rechazar Ho en el nivel de significancia 0.05”. Siempre debes redactar tu conclusión en términos de los datos. Aunque usaremos la terminología de “rechazar a Ho” o “no rechazar a Ho”, esto se debe principalmente a que te estamos instruyendo en estos conceptos. En la práctica, este lenguaje rara vez se usa. También sugerimos escribir su conclusión en términos de la hipótesis alternativa. ¿Hay o no hay suficiente evidencia de que la hipótesis alternativa es cierta?

   ---

3. Volvamos al tema de la naturaleza de los dos tipos de conclusiones que puedo hacer.

• O rechazo Ho (cuando el valor p es menor que el nivel de significancia)
• o no puedo rechazar Ho (cuando el valor p es mayor que el nivel de significancia).

Como mencionamos anteriormente, señalar que la segunda conclusión no implica que acepte a Ho, sino solo que no tengo pruebas suficientes para rechazarla. Decir (por error) “No tengo pruebas suficientes para rechazar a Ho así que lo acepto” indica que los datos proporcionan evidencia de que Ho es cierto, lo cual no es necesariamente el caso. Considere el siguiente ejemplo ligeramente artificial pero efectivo:

EJEMPLO:

Un patrón afirma suscribirse a una política de “igualdad de oportunidades”, no contratar a hombres con más frecuencia que a mujeres para puestos directivos. ¿Esto es creíble? No estás seguro, así que quieres probar las siguientes dos hipótesis:

• Ho: La proporción de directivos masculinos contratados es de 0.5
• Ha: La proporción de directivos masculinos contratados es superior a 0.5

Datos: Se elige al azar a tres de los nuevos directivos que fueron contratados en los últimos 5 años y encuentra que los 3 son hombres.

Evaluación de Evidencia: Si la proporción de directivos masculinos contratados es realmente 0.5 (Ho es cierto), entonces la probabilidad de que la selección aleatoria de tres directivos arroje tres varones es por lo tanto 0.5 * 0.5 * 0.5 = 0.125. Este es el valor p (usando la regla de multiplicación para eventos independientes).

Conclusión: Usando 0.05 como nivel de significancia, se concluye que dado que el valor p = 0.125 > 0.05, el hecho de que los tres gerentes seleccionados al azar fueran todos varones no es evidencia suficiente para rechazar la afirmación del empleador de suscribirse a una política de igualdad de oportunidades (Ho).

Sin embargo, los datos (los tres seleccionados son varones) definitivamente NO proporcionan pruebas para aceptar la reclamación del empleador (Ho).

Aprender haciendo: Usar valores p

¿Conseguí esto? : Usando valores p

Comentario sobre la redacción: Otra redacción común en las revistas científicas es:

• “Los resultados son estadísticamente significativos” — cuando el valor p < α (alfa).
• “Los resultados no son estadísticamente significativos” — cuando el valor p > α (alfa).

A menudo verá niveles de significancia reportados con descripción adicional para indicar el grado de significancia estadística. Una pauta general (aunque no requerida en nuestro curso) es:

• Si 0.01 ≤ valor p < 0.05, entonces los resultados son (estadísticamente) significativos.
• Si 0.001 ≤ valor p < 0.01, entonces los resultados son altamente estadísticamente significativos.
• Si el valor p < 0.001, entonces los resultados son muy altamente estadísticamente significativos.
• Si el valor p > 0.05, entonces los resultados no son estadísticamente significativos (NS).
• Si 0.05 ≤ valor p < 0.10, entonces los resultados son marginalmente estadísticamente significativos.

Vamos a resumir

Aprendimos bastante sobre las pruebas de hipótesis. Aprendimos la lógica detrás de esto, cuáles son los elementos clave y qué tipo de conclusiones podemos y no podemos sacar en las pruebas de hipótesis. Aquí hay un resumen rápido:

Video

Video: Resumen de las Pruebas de Hipótesis (2:20)

Aquí hay algunas actividades más si necesitas alguna práctica adicional.

¿Conseguí esto? : Resumen de las pruebas de hipótesis

Comentarios:

• Observe que el valor p es un ejemplo de probabilidad condicional. Calculamos la probabilidad de obtener resultados como los de nuestros datos (o más extremos) DANDO que la hipótesis nula es verdadera. Podríamos escribir P (Obteniendo resultados como los nuestros o más extremos | Ho is True).

• Otra frase común utilizada para definir el valor p es: “La probabilidad de obtener una estadística como o más extrema que su resultado dada la hipótesis nula es VERDADERA”.
  • Podríamos escribir P (Obtención de un estadístico de prueba como o más extremo que el nuestro | Ho is True).
  • En este caso nos estamos preguntando “Suponiendo que la hipótesis nula es cierta, ¿qué tan raro es observar algo tan o más extremo que lo que he encontrado en mis datos?”
  • Si después de asumir la hipótesis nula es cierta, lo que hemos encontrado en nuestros datos es extremadamente raro (pequeño valor p), esto proporciona evidencia para rechazar nuestra suposición de que Ho es cierto a favor de Ha.

• El valor p también puede pensarse como la probabilidad, asumiendo que la hipótesis nula es verdadera, que el resultado que hemos visto se debe únicamente a un error aleatorio (o azar azar). Ya hemos visto que las estadísticas de muestras recolectadas de una población varían. Hay error aleatorio o probabilidad aleatoria involucrada cuando se toma una muestra de poblaciones.

En esta configuración, si el valor p es muy pequeño, esto implica, asumiendo que la hipótesis nula es cierta, que es extremadamente improbable que los resultados que hemos obtenido hubieran ocurrido solo por error aleatorio, y así nuestra suposición (Ho) es rechazada a favor de la hipótesis alternativa (Ha).

• Es EXTREMADAMENTE importante que encuentres una definición del valor p que tenga sentido para ti. Los nuevos estudiantes a menudo necesitan contemplar esta idea repetidamente a través de una variedad de ejemplos y explicaciones antes de sentirse cómodos con esta idea. Es uno de los dos conceptos más importantes en estadística (siendo el otro los intervalos de confianza).

Recuerda:

• Inferimos que la hipótesis alternativa es verdadera SOLAMENTE rechazando la hipótesis nula.
• Un resultado estadísticamente significativo es aquel que tiene una probabilidad muy baja de ocurrir si la hipótesis nula es verdadera.
• Los resultados estadísticamente significativos pueden tener o no significancia práctica y viceversa.

Error y potencia

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.28: Definir un error Tipo I y Tipo II en general y en el contexto de escenarios específicos.

Objetivos de aprendizaje

LO 6.29: Explicar el concepto del poder de una prueba estadística incluyendo la relación entre la potencia, el tamaño de la muestra y el tamaño del efecto.

Video

Video: Errores y Poder (12:03)

Errores Tipo I y Tipo II en Pruebas de Hipótesis

Todavía no hemos discutido el hecho de que no se nos garantiza tomar la decisión correcta por este proceso de prueba de hipótesis. A lo mejor se empieza a ver que siempre hay cierto nivel de incertidumbre en las estadísticas.

Pensemos en lo que ya sabemos y definamos los posibles errores que podemos cometer en las pruebas de hipótesis. Cuando realizamos una prueba de hipótesis, elegimos una de las dos posibles conclusiones basadas en nuestros datos.

Si el valor p es menor que su nivel de significancia previamente especificado (α, alfa), rechaza la hipótesis nula y

• Has tomado la decisión correcta ya que la hipótesis nula es falsa

O

• Has cometido un error (Tipo I) y rechazado Ho cuando de hecho Ho es cierto (tus datos resultaron ser un EVENTO RARO bajo Ho)

Si el valor p es mayor que (o igual a) su nivel de significancia elegido (α, alfa), no puede rechazar la hipótesis nula y

• Has tomado la decisión correcta ya que la hipótesis nula es verdadera

O

• Has cometido un error (Tipo II) y no has rechazado a Ho cuando de hecho Ho es falso (la hipótesis alternativa, Ha, es cierta)

A continuación se resumen los cuatro posibles resultados que se pueden obtener de una prueba de hipótesis. Observe que las filas representan la decisión tomada en la prueba de hipótesis y las columnas representan la verdad (generalmente desconocida) en la realidad.

Si bien en la práctica se desconoce la verdad —o no estaríamos realizando la prueba— sabemos que debe darse el caso de que o la hipótesis nula es verdadera o la hipótesis nula es falsa. ¡También es el caso de que cualquiera de las decisiones que tomemos en una prueba de hipótesis puede resultar en una conclusión incorrecta!

UN Error TIPO I ocurre cuando Rechazamos Ho cuando, de hecho, Ho es Verdadero. En este caso, rechazamos erróneamente una verdadera hipótesis nula.

• P (Error TIPO I) = P (Rechazar Ho | Ho es Verdadero) = α = alfa = Nivel de significancia

Un Error TIPO II ocurre cuando fallamos en Rechazar Ho cuando, de hecho, Ho es Falso. En este caso fallamos en rechazar una falsa hipótesis nula.

• P (Error TIPO II) = P (No Rechazar Ho | Ho es Falso) = β = beta

Cuando nuestro nivel de significancia es del 5%, estamos diciendo que nos vamos a permitir hacer un error de Tipo I menos del 5% de las veces. A la larga, si repetimos el proceso, el 5% de las veces encontraremos un valor p < 0.05 cuando de hecho la hipótesis nula era verdadera.

En este caso, nuestros datos representan una ocurrencia rara que es poco probable que suceda pero aún es posible. Por ejemplo, supongamos que tiramos una moneda 10 veces y obtenemos 10 cabezas, esto es poco probable para una moneda justa pero no imposible. Podríamos concluir que la moneda es injusta cuando de hecho simplemente vimos un evento muy raro para esta moneda justa.

Nuestro procedimiento de prueba CONTROLA el error Tipo I cuando establecemos un valor predeterminado para el nivel de significancia.

Observe que estas probabilidades son probabilidades condicionales. Esta es una razón más por la que la probabilidad condicional es un concepto importante en la estadística.

Desafortunadamente, calcular la probabilidad de un error Tipo II requiere que conozcamos la verdad sobre la población. En la práctica solo podemos calcular esta probabilidad usando una serie de cálculos “qué pasaría si” que dependen del tipo de problema.

Precaución

Comentario: Como inicialmente lees a través de los ejemplos a continuación, concéntrese en los conceptos amplios en lugar de los pequeños detalles. No es importante entender cómo calcular estos valores usted mismo en este punto.

• Intenta entender las fotos que te presentamos. ¿Qué imágenes representan una hipótesis nula supuesta y cuáles representan una alternativa?
• Puede ser útil volver a esta página (y a las actividades aquí) después de haber revisado el resto de la sección sobre pruebas de hipótesis y haber trabajado algunos problemas usted mismo.

Applet interactivo: significancia estadística

Aquí hay dos ejemplos del uso de una versión anterior de este applet. Se ve ligeramente diferente pero los mismos ajustes y opciones están disponibles en la versión anterior.

En ambos casos consideraremos puntajes de CI.

Nuestra hipótesis nula es que la verdadera media es 100. Supongamos que la desviación estándar es 16 y especificaremos un nivel de significancia del 5%.

EJEMPLO:

En este ejemplo especificaremos que la verdadera media es efectivamente 100 para que la hipótesis nula sea verdadera. La mayoría de las veces (95%), cuando generamos una muestra, debemos dejar de rechazar la hipótesis nula ya que la hipótesis nula es efectivamente cierta.

Aquí hay una muestra que resulta en una decisión correcta:

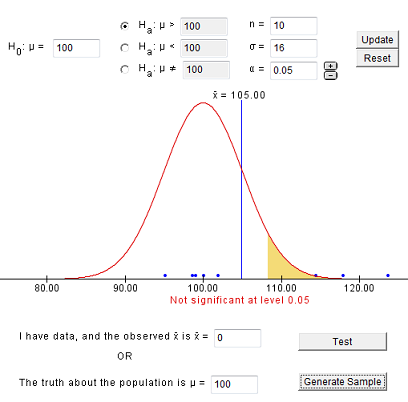
En la muestra anterior, obtenemos una barra x de 105, que se dibuja sobre la distribución que asume μ (mu) = 100 (la hipótesis nula es verdadera). Observe que la muestra se muestra como puntos azules a lo largo del eje x y la región sombreada muestra para qué valores de barra x rechazaríamos la hipótesis nula. En otras palabras, rechazaríamos a Ho siempre que la barra x caiga en la región sombreada.

Ingresa los mismos valores y genera muestras hasta obtener un error Tipo I (rechazas falsamente la hipótesis nula). Deberías ver algo como esto:

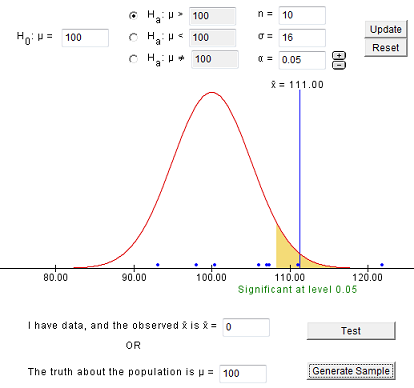
Si tuvieras que generar 100 muestras, deberías tener alrededor del 5% donde rechazaste a Ho. Estas serían muestras que resultarían en un error de Tipo I.

El ejemplo anterior ilustra una decisión correcta y un error de Tipo I cuando la hipótesis nula es verdadera. El siguiente ejemplo ilustra una decisión correcta y un error Tipo II cuando la hipótesis nula es falsa. En este caso, debemos especificar la verdadera media poblacional.

EJEMPLO:

Supongamos que estamos muestreando de un programa de honores y que el verdadero coeficiente intelectual medio para esta población es de 110. Desconocemos la probabilidad de un error Tipo II sin cálculos más detallados.

Comencemos con una muestra que resulte en una decisión correcta.

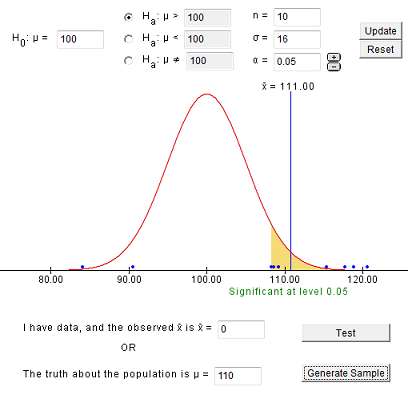
En la muestra anterior, obtenemos una barra x de 111, que se dibuja sobre la distribución que asume μ (mu) = 100 (la hipótesis nula es verdadera).

Ingresa los mismos valores y genera muestras hasta obtener un error Tipo II (no rechazas la hipótesis nula). Deberías ver algo como esto:

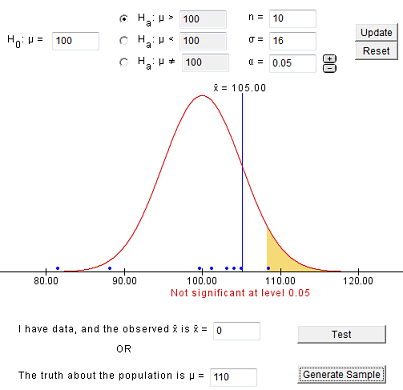
Debes notar que en este caso (cuando Ho es falso), es más fácil obtener una decisión incorrecta (un error de Tipo II) que en el caso en que Ho es cierto. Si generas 100 muestras, puedes aproximar la probabilidad de un error Tipo II.

Podemos encontrar la probabilidad de un error Tipo II visualizando conjuntamente tanto la distribución supuesta como la distribución verdadera. La imagen de abajo está adaptada a partir de un applet que usaremos cuando discutamos el poder de una prueba estadística.

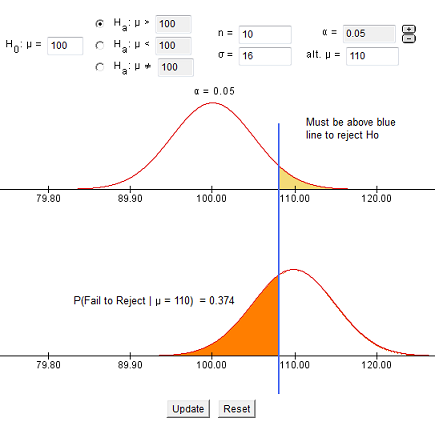
Existe un 37.4% de probabilidad de que, a la larga, cometamos un error de Tipo II y no rechacemos la hipótesis nula cuando de hecho el verdadero coeficiente intelectual medio es de 110 en la población de la que tomamos muestras de nuestros 10 individuos.

¿Se puede visualizar qué pasará si la verdadera media poblacional es realmente 115 o 108? ¿Cuándo aumentará el error Tipo II? ¿Cuándo disminuirá? Volveremos a mirar esta idea cuando discutamos el concepto de poder en pruebas de hipótesis.

Comentarios:

• Es importante señalar que existe una compensación entre la probabilidad de un error de Tipo I y de Tipo II. Si disminuimos la probabilidad de uno de estos errores, ¡la probabilidad del otro aumentará! El resultado práctico de esto es que si requerimos evidencia más fuerte para rechazar la hipótesis nula (menor nivel de significancia = probabilidad de un error de Tipo I), aumentaremos la probabilidad de que no podamos rechazar la hipótesis nula cuando de hecho Ho es falso (aumenta la probabilidad de un error de Tipo II).

• Cuando α (alfa) = 0.05 obtuvimos una probabilidad de error Tipo II de 0.374 = β = beta

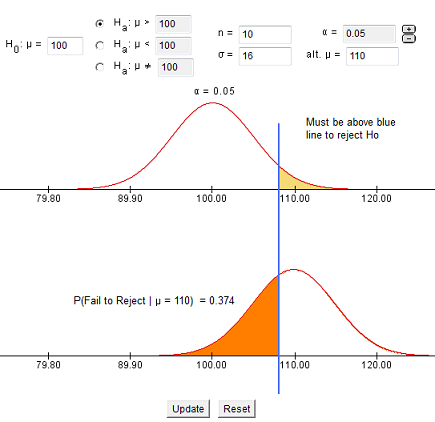
• Cuando α (alfa) = 0.01 (menor que antes) obtenemos una probabilidad de error Tipo II de 0.644 = β = beta (mayor que antes)

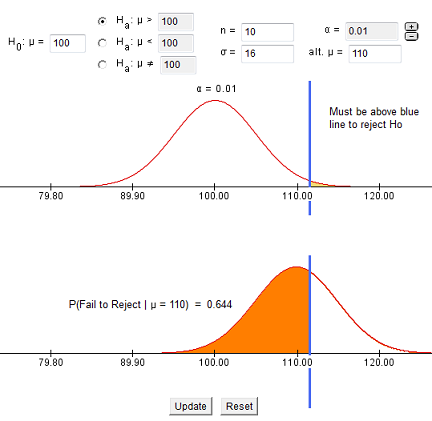
• A medida que la línea azul en la imagen se mueve más hacia la derecha, el nivel de significancia (α, alfa) disminuye y la probabilidad de error de Tipo II va en aumento.

• A medida que la línea azul de la imagen se mueve más a la izquierda, el nivel de significancia (α, alfa) aumenta y la probabilidad de error de Tipo II disminuye

Volvamos a nuestro primer ejemplo y definamos estos dos errores en contexto.

EJEMPLO:

Un caso de sospecha de trampa en un examen se presenta ante el comité disciplinario de una determinada universidad.

Hay dos pretensiones opuestas en este caso:

• Ho = La afirmación del alumno: No hice trampa en el examen.

• Ha = La afirmación del instructor: El alumno hizo trampa en el examen.

Adhiriéndose al principio de “inocente hasta que se demuestre su culpabilidad”, el comité pide al instructor pruebas que respalden su afirmación.

Hay cuatro posibles resultados de este proceso. Hay dos posibles decisiones correctas:

• El alumno hizo trampa en el examen y el instructor trae pruebas suficientes para rechazar a Ho y concluir que el alumno hizo trampa en el examen. ¡Esta es una decisión CORRECTA!

• El alumno no hizo trampa en el examen y el instructor no aporta pruebas suficientes de que el alumno hizo trampa en el examen. ¡Esta es una decisión CORRECTA!

Tanto las decisiones correctas como los posibles errores son bastante fáciles de entender pero con los errores, hay que tener cuidado de identificar y definir los dos tipos correctamente.

Error TIPO I: Rechazar Ho cuando Ho es Verdadero

• El alumno no hizo trampa en el examen pero el instructor trae pruebas suficientes para rechazar a Ho y concluir que el alumno engañó en el examen. Este es un Error de Tipo I.

Error TIPO II: Error al Rechazar Ho cuando Ho es Falso

• El alumno hizo trampa en el examen pero el instructor no proporciona suficientes pruebas de que el estudiante hizo trampa en el examen. Este es un Error Tipo II.

En la mayoría de las situaciones, incluyendo esta, es más “aceptable” tener un error de Tipo II que un error de Tipo I. Si bien permitir que un estudiante que engaña quede impune podría considerarse un problema muy malo, castigar a un estudiante por algo que no hizo suele considerarse un error más grave. Esta es una de las razones por las que controlamos nuestro error Tipo I en el proceso de prueba de hipótesis.

¿Conseguí esto? : Errores Tipo I y Tipo II (en contexto)

Comentario:

• Las probabilidades de errores Tipo I y Tipo II están estrechamente relacionadas con los conceptos de sensibilidad y especificidad que discutimos anteriormente. Considere las siguientes hipótesis:

Ho: El individuo no tiene diabetes (status quo, no pasa nada especial)

Ja: El individuo sí tiene diabetes (algo está pasando aquí)

En esta configuración:

Cuando alguien da positivo por diabetes rechazaríamos la hipótesis nula y concluiríamos que la persona tiene diabetes (¡podemos o no estar en lo correcto!).

Cuando alguien da negativo para diabetes no rechazaríamos la hipótesis nula para no concluir que la persona tiene diabetes (¡podemos o no estar en lo correcto!)

Vamos un paso más allá:

Sensibilidad = P (Test + | Tener Enfermedad) que en este ajuste es igual a
P (Rechazar Ho | Ho es Falso) = 1 — P (No Rechazar Ho | Ho es Falso) = 1 — β = 1 — beta

Especificidad = P (Prueba — | Sin enfermedad) que en este escenario es igual a
P (No Rechazar Ho | Ho es Verdadero) = 1 — P (Rechazar Ho | Ho es Verdadero) = 1 — α = 1 — alfa

Observe que la sensibilidad y especificidad se relacionan con la probabilidad de tomar una decisión correcta, mientras que α (alfa) y β (beta) se relacionan con la probabilidad de tomar una decisión incorrecta.

Por lo general α (alfa) = 0.05 para que la especificidad enumerada anteriormente sea de 0.95 o 95%.

A continuación, veremos que la sensibilidad señalada anteriormente es el poder de la prueba de hipótesis!

Razones de un Error Tipo I en la Práctica

Suponiendo que ha obtenido una muestra de calidad:

• El motivo de un error de Tipo I es una probabilidad aleatoria.
• Cuando se produce un error Tipo I, nuestros datos observados representaban un evento raro que indicaba evidencia a favor de la hipótesis alternativa aunque la hipótesis nula era realmente cierta.

Razones para un Error Tipo II en la Práctica

Nuevamente, asumiendo que ha obtenido una muestra de calidad, ahora tenemos algunas posibilidades dependiendo de la verdadera diferencia que exista.

• El tamaño de la muestra es demasiado pequeño para detectar una diferencia importante. Este es el peor de los casos, deberías haber obtenido una muestra más grande. En esta situación, puede notar que el efecto visto en la muestra parece PRACTICAMENTE significativo y sin embargo el valor p no es lo suficientemente pequeño como para rechazar la hipótesis nula.

• El tamaño de la muestra es razonable para la diferencia importante pero la verdadera diferencia (que podría ser algo significativa o interesante) es menor de lo que su prueba fue capaz de detectar. Esto es tolerable ya que no estabas interesado en poder detectar esta diferencia cuando iniciaste tu estudio. En esta situación, puede notar que el efecto visto en la muestra parece tener algún potencial de significación práctica.

• El tamaño muestral es más que adecuado, la diferencia que no se detectó carece de sentido en la práctica. Esto no es un problema en absoluto y en efecto es una “decisión correcta” ya que la diferencia que no detectaste no tendría sentido práctico.
• Nota: Más adelante discutiremos con más detalle la idea de significación práctica.

El poder de una prueba de hipótesis

A menudo sucede que realmente deseamos probar la hipótesis alternativa. Es razonable que nos interese la probabilidad de rechazar correctamente la hipótesis nula. Es decir, la probabilidad de rechazar la hipótesis nula, cuando de hecho la hipótesis nula es falsa. Esto también se puede considerar como la probabilidad de poder detectar una diferencia (preespecificada) de interés para el investigador.

Comencemos con un ejemplo realista de cómo se puede describir el poder en un estudio.

EJEMPLO:

En un ensayo clínico para estudiar dos medicamentos para bajar de peso, tenemos un 80% de probabilidad de detectar una diferencia en la pérdida de peso entre los dos medicamentos de 10 libras. Es decir, el poder de la prueba de hipótesis que realizaremos es del 80%.

Es decir, si un medicamento proviene de una población con una pérdida de peso promedio de 25 libras y el otro proviene de una población con una pérdida de peso promedio de 15 libras, tendremos un 80% de probabilidad de detectar esa diferencia utilizando la muestra que tenemos en nuestro ensayo.

Si tuviéramos que repetir este ensayo muchas veces, 80% de las veces podremos rechazar la hipótesis nula (que no hay diferencia entre los medicamentos) y 20% de las veces fallaremos en rechazar la hipótesis nula (¡y hacer un error de Tipo II!).

La diferencia de 10 libras en el ejemplo anterior, a menudo se llama el tamaño del efecto. La medida del efecto difiere dependiendo de la prueba particular que estés realizando pero siempre es alguna medida relacionada con el verdadero efecto en la población. En este ejemplo, es la diferencia entre dos medias poblacionales.

Recordemos la definición de un error Tipo II:

Un Error TIPO II ocurre cuando fallamos en Rechazar Ho cuando, de hecho, Ho es Falso. En este caso fallamos en rechazar una falsa hipótesis nula.

P (Error TIPO II) = P (No Rechazar Ho | Ho es Falso) = β = beta

Observe que P (Rechazar Ho | Ho es Falso) = 1 — P (No Rechazar Ho | Ho es Falso) = 1 — β = 1- beta.

El PODER de una prueba de hipótesis es la probabilidad de rechazar la hipótesis nula cuando la hipótesis nula es falsa. Esto también se puede afirmar como la probabilidad de rechazar correctamente la hipótesis nula.

PODER = P (Rechazar Ho | Ho es Falso) = 1 — β = 1 — beta

El poder es la capacidad de la prueba para rechazar correctamente la hipótesis nula. Una prueba con alta potencia tiene buenas posibilidades de poder detectar la diferencia de interés para nosotros, si existe.

Como mencionamos en la parte inferior de la página anterior, esto puede pensarse como la sensibilidad de la prueba de hipótesis si imaginas Ho = Sin enfermedad y Ha = Enfermedad.

Factores que afectan el poder de una prueba de hipótesis

El poder de una prueba de hipótesis se ve afectado por numerosas cantidades (similar al margen de error en un intervalo de confianza).

Supongamos que la hipótesis nula es falsa para una prueba de hipótesis dada. Todo lo demás siendo iguales, tenemos lo siguiente:

• Muestras más grandes dan como resultado una mayor probabilidad de rechazar la hipótesis nula, lo que significa un aumento en el poder de la prueba de hipótesis.

• Si el tamaño del efecto es mayor, nos resultará más fácil detectarlo. Esto da como resultado una mayor probabilidad de rechazar la hipótesis nula lo que significa un aumento en el poder de la prueba de hipótesis. El tamaño del efecto varía para cada prueba y suele estar estrechamente relacionado con la diferencia entre el valor hipotético y el valor verdadero del parámetro en estudio.

• De la relación entre la probabilidad de un error Tipo I y un Tipo II (a medida que α (alfa) disminuye, β (beta) aumenta), podemos ver que a medida que α (alfa) disminuye, Potencia = 1 — β = 1 — beta también disminuye.

• Existen otras formas matemáticas de cambiar el poder de una prueba de hipótesis, como cambiar la desviación estándar de la población; sin embargo, estas no son cantidades que usualmente podamos controlar por lo que no las discutiremos aquí.

Precaución

En la práctica, especificamos un nivel de significancia y una potencia deseada para detectar una diferencia que tendrá un significado práctico para nosotros y esto determina el tamaño de muestra requerido para el experimento o estudio.

Para la mayoría de las subvenciones que involucran análisis estadístico, se deben realizar cálculos de potencia para ilustrar que el estudio tendrá una probabilidad razonable de detectar un efecto importante. De lo contrario, el dinero gastado en el estudio podría desperdiciarse. El objetivo suele ser tener una potencia cercana al 80%.

Por ejemplo, si solo hay un 5% de probabilidad de detectar una diferencia importante entre dos tratamientos en un ensayo clínico, esto resultaría en una pérdida de tiempo, esfuerzo y dinero en el estudio ya que, cuando la hipótesis alternativa es cierta, la probabilidad de que se pueda encontrar un efecto del tratamiento es muy pequeña.

Comentario:

• Para calcular el poder de una prueba de hipótesis, debemos especificar la “verdad”. Como mencionamos anteriormente al discutir errores de Tipo II, en la práctica solo podemos calcular esta probabilidad usando una serie de cálculos “qué pasaría si” que dependen del tipo de problema.

La siguiente actividad implica trabajar con un applet interactivo para estudiar el poder con más detenimiento.

Aprender haciendo: El poder de las pruebas de hipótesis

La siguiente lectura es una excelente discusión sobre los errores Tipo I y Tipo II.

(Opcional) Lectura Exterior: Una Buena Discusión de Poder (≈ 2500 palabras)

No te estaremos pidiendo que realices cálculos de potencia manualmente. Se le puede pedir que utilice calculadoras y applets en línea. La mayoría de los paquetes de software estadístico ofrecen cierta capacidad para completar cálculos de potencia. También hay muchas calculadoras en línea para la potencia y el tamaño de la muestra en Internet, por ejemplo, la página de potencia y tamaño de muestra de Russ Lenth.

Proporciones (Introducción y Paso 1)

CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.

Objetivos de aprendizaje

LO 4.33: En un contexto dado, distinguir entre situaciones que involucran una proporción poblacional y una media poblacional y especificar la hipótesis nula y alternativa correcta para el escenario.

Objetivos de aprendizaje

LO 4.34: Realizar una prueba de hipótesis completa para una proporción poblacional a mano.

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Video

Video: Proporciones (Introducción y Paso 1) (7:18)

Ahora que entendemos el proceso de prueba de hipótesis y la lógica detrás del mismo, estamos listos para comenzar a aprender sobre pruebas estadísticas específicas (también conocidas como pruebas de significación).

La primera prueba que vamos a aprender es la prueba sobre la proporción poblacional (p).

Esta prueba es ampliamente conocida como la “prueba z para la proporción poblacional (p)”.

Introducción

Entenderemos más adelante de dónde viene la parte de la “prueba z”.

Este será el único tipo de problema que completarás completamente “a mano” en este curso. Nuestro objetivo es utilizar este ejemplo para darte las herramientas que necesitas para entender cómo funciona este proceso. Después de trabajar algunos problemas, deberías volver a revisar el material anterior. Es probable que necesite revisar la terminología y los conceptos varias veces antes de comprender completamente el proceso.

En realidad, a menudo estarás realizando pruebas estadísticas más complejas y permitiendo que el software proporcione el valor p. En estos escenarios será importante saber qué prueba aplicar para una situación determinada y poder explicar los resultados en contexto.

Revisión: Tipos de Variables

Cuando realizamos una prueba sobre una proporción poblacional, estamos trabajando con una variable categórica. Más adelante en el curso, después de haber aprendido una variedad de pruebas de hipótesis, necesitaremos poder identificar qué prueba es apropiada para qué situación. Identificar la variable como categórica o cuantitativa es un componente importante para elegir una prueba de hipótesis apropiada.

Aprender haciendo: Revisar tipos de variables

Prueba Z de una muestra para una proporción de población

En esta parte de nuestra discusión sobre las pruebas de hipótesis, entraremos en detalles que antes no entrábamos. Más específicamente, utilizaremos esta prueba para introducir la idea de un estadístico de prueba, y detalles sobre cómo se calculan los valores p.

Empecemos por introducir los tres ejemplos, que serán los ejemplos principales en nuestra discusión. A cada ejemplo le sigue una figura que ilustra la información proporcionada, así como la cuestión de interés.

EJEMPLO:

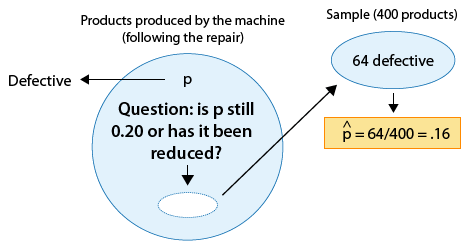
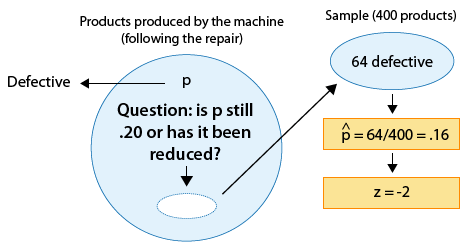
Se sabe que una máquina produce 20% de productos defectuosos y, por lo tanto, se envía para su reparación. Después de reparar la máquina, 400 productos producidos por la máquina se eligen al azar y 64 de ellos se encuentran defectuosos. ¿Los datos proporcionan suficiente evidencia de que la proporción de productos defectuosos producidos por la máquina (p) se ha reducido como resultado de la reparación?

La siguiente figura muestra la información, así como la cuestión de interés:

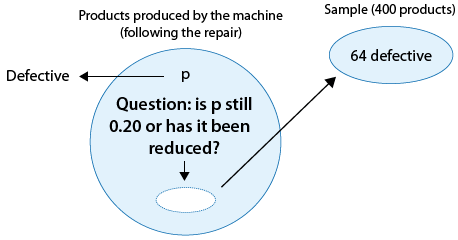
La cuestión de interés nos ayuda a formular las hipótesis nulas y alternativas en términos de p, la proporción de productos defectuosos producidos por la máquina después de la reparación:

Ho: p = 0.20 (Sin cambios; la reparación no ayudó).

Ha: p < 0.20 (La reparación fue efectiva para reducir la proporción de piezas defectuosas).

EJEMPLO:

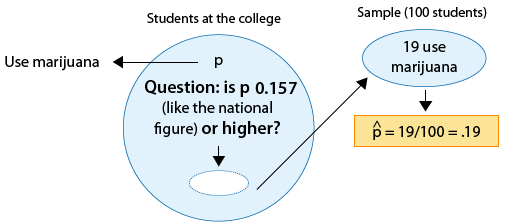
Hay rumores de que los estudiantes de cierta universidad de artes liberales están más inclinados a consumir drogas que los estudiantes universitarios estadounidenses en general. Supongamos que en una simple muestra aleatoria de 100 alumnos de la universidad, 19 admitieron el consumo de mariguana. ¿Los datos proporcionan evidencia suficiente para concluir que la proporción de consumidores de marihuana entre los estudiantes de la universidad (p) es mayor que la proporción nacional, que es 0.157? (Este número es reportado por la Escuela de Salud Pública de Harvard.)

Nuevamente, la siguiente figura muestra la información así como la cuestión de interés:

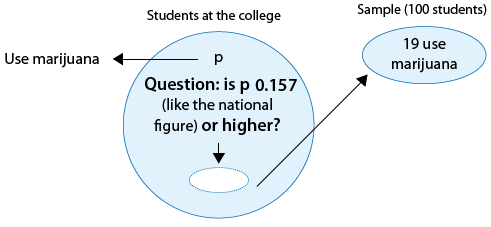
Como antes, podemos formular las hipótesis nulas y alternativas en términos de p, la proporción de estudiantes en la universidad que consumen mariguana:

Ho: p = 0.157 (igual que entre todos los universitarios del país).

Ha: p > 0.157 (superior a la cifra nacional).

EJEMPLO:

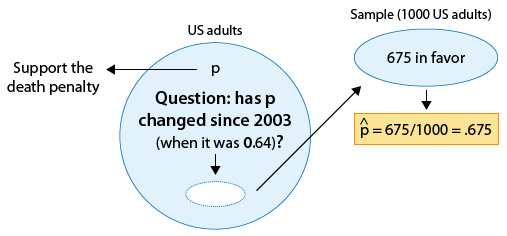
Las encuestas sobre ciertos temas se realizan de manera rutinaria con el fin de monitorear los cambios en las opiniones del público a lo largo del tiempo. Uno de esos temas es la pena de muerte. En 2003 una encuesta estimó que 64% de los adultos estadounidenses apoyan la pena de muerte para una persona condenada por asesinato. En una encuesta más reciente, 675 de cada mil adultos estadounidenses elegidos al azar estaban a favor de la pena de muerte para asesinos condenados. ¿Los resultados de esta encuesta proporcionan evidencia de que la proporción de adultos estadounidenses que apoyan la pena de muerte para asesinos condenados (p) cambió entre 2003 y la encuesta posterior?

Aquí hay una figura que muestra la información, así como la cuestión de interés:

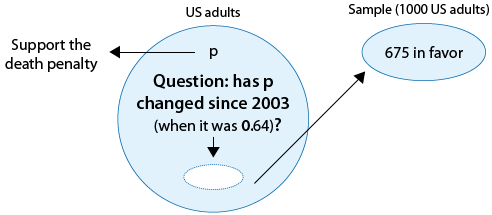
Nuevamente, podemos formular las hipótesis nulas y alternativas en términos de p, la proporción de adultos estadunidenses que apoyan la pena de muerte para asesinos condenados.

Ho: p = 0.64 (Sin cambios desde 2003).

Ha: p ≠ 0.64 (Algún cambio desde 2003).

Aprender haciendo: Proporciones (Resumen)

¿Conseguí esto? : Proporciones (Resumen)

Recordemos que básicamente hay 4 pasos en el proceso de prueba de hipótesis:

• PASO 1: Declarar las hipótesis nulas y alternativas apropiadas, Ho y Ha.
• PASO 2: Obtener una muestra aleatoria, recopilar datos relevantes y verificar si los datos cumplen con las condiciones bajo las cuales se puede usar la prueba. Si se cumplen las condiciones, resumir los datos utilizando un estadístico de prueba.
• PASO 3: Encuentra el valor p de la prueba.
• PASO 4: Con base en el valor p, decida si los resultados son estadísticamente significativos o no y saque sus conclusiones en contexto.
• Nota: En la práctica, siempre debemos considerar la significación práctica de los resultados así como la significancia estadística.

Ahora vamos a pasar por estos pasos ya que se aplican a la prueba de hipótesis para la proporción poblacional p. Cabe señalar que aunque los detalles serán específicos de esta prueba en particular, algunas de las ideas que agregaremos se aplican a las pruebas de hipótesis en general.

Paso 1. Aclarando las Hipótesis

Aquí nuevamente están los tres conjuntos de hipótesis que se están probando en cada uno de nuestros tres ejemplos:

EJEMPLO:

¿Se ha reducido la proporción de productos defectuosos como consecuencia de la reparación?

• Ho: p = 0.20 (Sin cambios; la reparación no ayudó).

• Ha: p < 0.20 (La reparación fue efectiva para reducir la proporción de piezas defectuosas).

EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

• Ho: p = 0.157 (igual que entre todos los universitarios del país).

• Ha: p > 0.157 (superior a la cifra nacional).

EJEMPLO:

¿La proporción de adultos estadounidenses que apoyan la pena de muerte cambió entre 2003 y una encuesta posterior?

• Ho: p = 0.64 (Sin cambios desde 2003).

• Ha: p ≠ 0.64 (Algún cambio desde 2003).

La hipótesis nula siempre toma la forma:

• Ho: p = algún valor

y la hipótesis alternativa adopta una de las tres formas siguientes:

• Ha: p < ese valor (como en el ejemplo 1) o

• Ha: p > ese valor (como en el ejemplo 2) o

• Ha: p ≠ ese valor (como en el ejemplo 3).

Obsérvese que quedó bastante claro a partir del contexto qué forma de la hipótesis alternativa sería apropiada. El valor que se especifica en la hipótesis nula se denomina valor nulo, y generalmente se denota con p ₀. Podemos decir, por lo tanto, que en general la hipótesis nula sobre la proporción poblacional (p) tomaría la forma:

• Ho: p = p ₀

Escribimos Ho: p = p ₀ para decir que estamos haciendo la hipótesis de que la proporción poblacional tiene el valor de p ₀. En otras palabras, p es la proporción de población desconocida y p ₀ es el número que pensamos que p podría ser para la situación dada.

La hipótesis alternativa adopta una de las siguientes tres formas (dependiendo del contexto):

• Ha: p < p ₀ (unilateral)

• Ha: p > p ₀ (unilateral)

• Ha: p ≠ p ₀ (bilateral)

Las dos primeras formas posibles de las alternativas (donde el signo = en Ho es desafiado por < or >) se denominan alternativas unilaterales, y la tercera forma de alternativa (donde el signo = en Ho es desafiado por ≠) se llama alternativa bilateral. Para entender la intuición detrás de estos nombres volvamos a nuestros ejemplos.

El ejemplo 3 (pena de muerte) es un caso en el que tenemos una alternativa bilateral:

• Ho: p = 0.64 (Sin cambios desde 2003).

• Ha: p ≠ 0.64 (Algún cambio desde 2003).

En este caso, para rechazar a Ho y aceptar a Ha necesitaremos obtener una muestra de proporción de partidarios de la pena de muerte que es muy diferente de 0.64 en cualquier dirección, ya sea mucho mayor o mucho menor que 0.64.

En el ejemplo 2 (consumo de marihuana) tenemos una alternativa unilateral:

• Ho: p = 0.157 (igual que entre todos los universitarios del país).

• Ha: p > 0.157 (superior a la cifra nacional).

Aquí, para rechazar a Ho y aceptar Ha necesitaremos obtener una proporción de muestra de consumidores de marihuana que es muy superior a 0.157.

Del mismo modo, en el ejemplo 1 (productos defectuosos), donde estamos probando:

• Ho: p = 0.20 (Sin cambios; la reparación no ayudó).

• Ha: p < 0.20 (La reparación fue efectiva para reducir la proporción de piezas defectuosas).

para rechazar Ho y aceptar Ha, necesitaremos obtener una proporción de muestra de productos defectuosos que es mucho menor a 0.20.

Aprender haciendo: Hipótesis estatales (proporciones)

¿Conseguí esto? : Hipótesis de Estado (Proporciones)

Proporciones (Paso 2)

CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.

Objetivos de aprendizaje

LO 4.33: En un contexto dado, distinguir entre situaciones que involucran una proporción poblacional y una media poblacional y especificar la hipótesis nula y alternativa correcta para el escenario.

Objetivos de aprendizaje

LO 4.34: Realizar una prueba de hipótesis completa para una proporción poblacional a mano.

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Video

Video: Proporciones (Paso 2) (12:38)

Paso 2. Recopilar datos, verificar condiciones y resumir datos

Una vez establecidas las hipótesis, el siguiente paso es obtener una muestra (en la que se basará la inferencia), recolectar datos relevantes y resumirlos.

Es sumamente importante que nuestra muestra sea representativa de la población sobre la que queremos sacar conclusiones. Esto se asegura cuando la muestra se elige al azar. Más allá de la cuestión práctica de garantizar la representatividad, elegir una muestra aleatoria tiene una importancia teórica que mencionaremos más adelante.

En el caso de las pruebas de hipótesis para la proporción poblacional (p), recopilaremos datos sobre la variable categórica relevante de los individuos de la muestra y comenzaremos calculando la proporción muestral p-hat (la cantidad natural a calcular cuando el parámetro de interés es p).

Volvamos a nuestros tres ejemplos y sumemos este paso a nuestras cifras.

EJEMPLO:

¿Se ha reducido la proporción de productos defectuosos como consecuencia de la reparación?

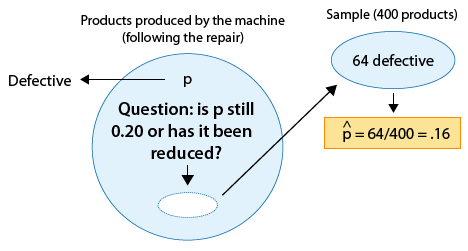
EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

EJEMPLO:

¿La proporción de adultos estadounidenses que apoyan la pena de muerte cambió entre 2003 y una encuesta posterior?

Como mencionamos anteriormente sin entrar en detalles, cuando resumimos los datos en pruebas de hipótesis, vamos un paso más allá de calcular el estadístico de muestra y resumimos los datos con un estadístico de prueba. Cada prueba tiene un estadístico de prueba, que hasta cierto punto captura la esencia de la prueba. De hecho, el valor p, que hasta ahora hemos visto como “el rey” (en el sentido de que todo está determinado por él), en realidad está determinado por (o derivado de) el estadístico de prueba. Ahora presentaremos el estadístico de prueba.

El estadístico de prueba es una medida de lo lejos que está la proporción muestral p-hat del valor nulo p ₀, el valor que afirma la hipótesis nula es el valor de p. Es decir, dado que p-hat es lo que los datos estiman p a ser, el estadístico de prueba puede verse como una medida de la “distancia” entre lo que los datos nos dicen sobre p y lo que la hipótesis nula afirma ser p.

Usemos nuestros ejemplos para entender esto:

EJEMPLO:

¿Se ha reducido la proporción de productos defectuosos como consecuencia de la reparación?

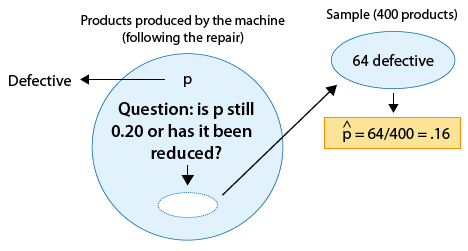
El parámetro de interés es p, la proporción de productos defectuosos después de la reparación.

La estimación de datos p para ser p-hat = 0.16

La hipótesis nula afirma que p = 0.20

Por lo tanto, los datos están 0.04 (o 4 puntos porcentuales) por debajo del valor de hipótesis nula.

Es difícil evaluar si esta diferencia de 4% en productos defectuosos es evidencia suficiente para decir que la reparación fue efectiva para reducir la proporción de productos defectuosos, pero claramente, cuanto mayor sea la diferencia, más evidencia es contra la hipótesis nula. Entonces, si, por ejemplo, nuestra proporción muestral de productos defectuosos hubiera sido, digamos, 0.10 en lugar de 0.16, entonces creo que todos estarían de acuerdo en que reducir la proporción de productos defectuosos a la mitad (de 20% a 10%) sería evidencia extremadamente fuerte de que la reparación fue efectiva para reducir la proporción de defectuosos productos.

EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

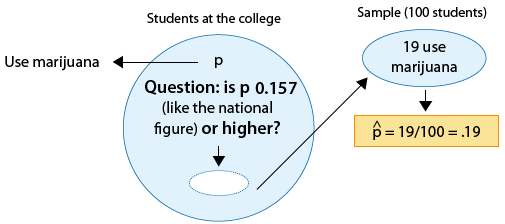
El parámetro de interés es p, la proporción de estudiantes de una universidad que consumen mariguana.

La estimación de datos p para ser p-hat = 0.19

La hipótesis nula afirma que p = 0.157

Por lo tanto, los datos están 0.033 (o 3.3. puntos porcentuales) por encima del valor de hipótesis nula.

EJEMPLO:

¿La proporción de adultos estadounidenses que apoyan la pena de muerte cambió entre 2003 y una encuesta posterior?

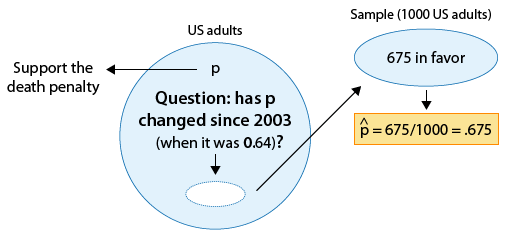
El parámetro de interés es p, la proporción de adultos estadounidenses que apoyan la pena de muerte para asesinos condenados.

La estimación de datos p para ser p-hat = 0.675

La hipótesis nula afirma que p = 0.64

Hay una diferencia de 0.035 (o 3.5. puntos porcentuales) entre los datos y el valor de hipótesis nula.

El problema de mirar solo la diferencia entre la proporción muestral, p-hat, y el valor nulo, p ₀ es que no hemos tomado en cuenta la variabilidad de nuestro estimador p-hat que, como sabemos por nuestro estudio de distribuciones muestrales, depende del tamaño de la muestra.

Por esta razón, el estadístico de prueba no puede ser simplemente la diferencia entre p-hat y p ₀, sino que debe ser alguna forma de esa fórmula que tenga en cuenta el tamaño de la muestra. Es decir, necesitamos de alguna manera estandarizar la diferencia para que sea posible la comparación entre diferentes situaciones. Estamos muy cerca de revelar el estadístico de prueba, pero antes de construirlo, recordemos los siguientes dos hechos de probabilidad:

Dato 1: Cuando tomamos una muestra aleatoria de tamaño n de una población con proporción poblacional p, entonces

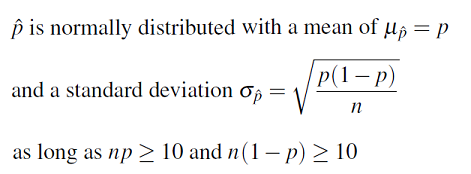
Hecho 2: La puntuación z de cualquier valor normal (un valor que proviene de una distribución normal) se calcula encontrando la diferencia entre el valor y la media y luego dividiendo esa diferencia por la desviación estándar (de la distribución normal asociada al valor). La puntuación z representa cuántas desviaciones estándar por debajo o por encima de la media es el valor.

Por lo tanto, nuestro estadístico de prueba debe ser una medida de qué tan lejos está la proporción muestral p-hat del valor nulo p ₀ relativo a la variación de p-hat (medida por el error estándar de p-hat).

Recordemos que el error estándar es la desviación estándar de la distribución de muestreo para un estadístico dado. Para p-hat, conocemos lo siguiente:

Para encontrar el valor p, necesitaremos determinar cuán sorprendente es nuestro valor asumiendo que la hipótesis nula es verdadera. Ya contamos con las herramientas necesarias para este proceso a partir de nuestro estudio de distribuciones de muestreo como se representa en la tabla anterior.

EJEMPLO:

¿Se ha reducido la proporción de productos defectuosos como consecuencia de la reparación?

Si asumimos que la hipótesis nula es verdadera, podemos especificar que el centro de la distribución de todos los valores posibles de p-hat a partir de muestras de tamaño 400 sería 0.20 (nuestro valor nulo).

Podemos calcular el error estándar, asumiendo p = 0.20 como

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}=\sqrt{\dfrac{0.2(1-0.2)}{400}}=0.02\)

El siguiente cuadro representa la distribución muestral de todos los valores posibles de p-hat de muestras de tamaño 400, asumiendo que la verdadera proporción p es 0.20 y se cumplen nuestros otros requisitos para que la distribución muestral sea normal (los revisaremos durante el siguiente paso).

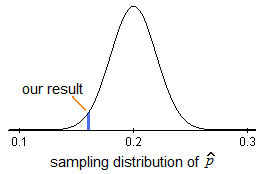
Para poder calcular las probabilidades para la imagen de arriba, necesitaríamos encontrar la puntuación z asociada a nuestro resultado.

¡Este puntaje z es el estadístico de prueba! En este ejemplo, el numerador de nuestra puntuación z es la diferencia entre p-hat (0.16) y el valor nulo (0.20) que antes encontramos que era -0.04. El denominador de nuestro puntaje z es el error estándar calculado anteriormente (0.02) y así rápidamente encontramos que el puntaje z, nuestro estadístico de prueba, es -2.

La proporción muestral basada en estos datos es de 2 errores estándar por debajo del valor nulo.

Ojalá ahora entiendas más sobre las razones por las que necesitamos probabilidad en estadística!!

Ahora formalizaremos la definición y veremos nuestros ejemplos restantes antes de pasar al siguiente paso, que será determinar si se aplica una distribución normal y calcular el valor p.

El estadístico de prueba para pruebas de hipótesis para una proporción es:

\(z=\dfrac{\hat{p}-p_{0}}{\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}}\)

Representa la diferencia entre la proporción muestral y el valor nulo, medido en desviaciones estándar (error estándar de p-hat).

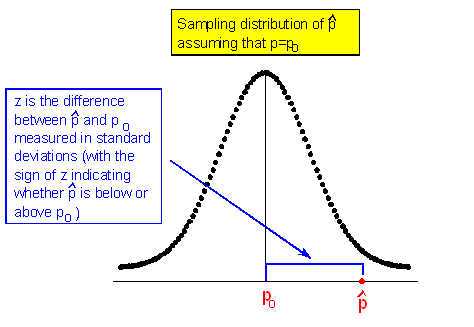
La imagen de arriba es una representación de la distribución de muestreo de p-hat asumiendo p = p ₀. En otras palabras, este es un modelo de cómo se comporta p-hat si estamos dibujando muestras aleatorias de una población para la que Ho es cierto.

Observe que el centro de la distribución muestral está en p ₀, que es la proporción hipotética dada en la hipótesis nula (Ho: p = p ₀.) También podríamos marcar el eje en unidades de error estándar,

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}\)

Por ejemplo, si nuestra hipótesis nula afirma que la proporción de adultos estadounidenses que apoyan la pena de muerte es de 0.64, entonces la distribución muestral se dibuja como si el nulo fuera cierto. Dibujamos una distribución normal centrada en 0.64 (p ₀) con un error estándar dependiente del tamaño de la muestra,

\(\sqrt{\dfrac{0.64(1-0.64)}{n}}\).

Comentario Importante:

• Obsérvese que bajo el supuesto de que Ho es verdadero (y si se cumplen las condiciones para que la distribución muestral sea normal) el estadístico de prueba sigue una distribución N (0,1) (normal estándar). Otra forma de decir lo mismo que es bastante común es: “La distribución nula del estadístico de prueba es N (0,1)”.

Por “distribución nula”, nos referimos a la distribución bajo el supuesto de que Ho es cierto. Como veremos y volveremos a estresar más adelante, la distribución nula del estadístico de prueba es en lo que se basa el cálculo del valor p.

Volvamos a nuestros dos ejemplos restantes y encontremos el estadístico de prueba en cada caso:

EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

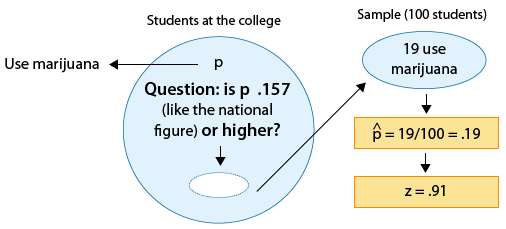
Dado que la hipótesis nula es Ho: p = 0.157, la puntuación estandarizada (z) de p-hat = 0.19 es

\(z=\dfrac{0.19-0.157}{\sqrt{\dfrac{0.157(1-0.157)}{100}}} \approx 0.91\)

Este es el valor del estadístico de prueba para este ejemplo.

Interpretamos esto para significar que, asumiendo que Ho es cierto, la proporción muestral p-hat = 0.19 es 0.91 errores estándar por encima del valor nulo (0.157).

EJEMPLO:

¿La proporción de adultos estadounidenses que apoyan la pena de muerte cambió entre 2003 y una encuesta posterior?

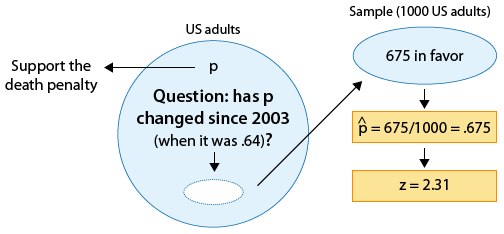
Dado que la hipótesis nula es Ho: p = 0.64, la puntuación estandarizada (z) de p-hat = 0.675 es

\(z=\dfrac{0.675-0.64}{\sqrt{\dfrac{0.64(1-0.64)}{1000}}} \approx 2.31\)

Este es el valor del estadístico de prueba para este ejemplo.

Interpretamos esto para significar que, asumiendo que Ho es cierto, la proporción muestral p-hat = 0.675 es 2.31 errores estándar por encima del valor nulo (0.64).

Aprender haciendo: Proporciones (Paso 2)

Comentarios sobre el Test Statistic:

• Mencionamos anteriormente que hasta cierto punto, el estadístico de prueba captura la esencia de la prueba. En este caso, el estadístico de prueba mide la diferencia entre p-hat y p ₀ en errores estándar. De esto es exactamente de lo que trata esta prueba. Obtener datos, y observar la discrepancia entre lo que los datos estiman p para ser (representado por p-hat) y lo que Ho afirma sobre p (representado por p ₀).
• Se puede pensar en este estadístico de prueba como medida de evidencia en los datos contra Ho. Cuanto mayor sea el estadístico de prueba, “más lejos están los datos de Ho” y por lo tanto más evidencia proporcionan los datos contra Ho.

Aprende haciendo: Proporciones (Paso 2) Comprender la Estadística de Prueba

¿Conseguí esto? : Proporciones (Paso 2)

Comentarios:

• Ahora debería quedar claro por qué esta prueba se conoce comúnmente como la prueba z para la proporción poblacional. El nombre proviene del hecho de que se basa en un estadístico de prueba que es un puntaje z.

• Recordemos el hecho 1 que usamos para construir el estadístico z-test. Aquí vuelve a formar parte de ello:

Cuando tomamos una muestra aleatoria de tamaño n de una población con proporción poblacional p ₀, los posibles valores de la proporción muestral p-hat (cuando se cumplen ciertas condiciones) tienen aproximadamente una distribución normal con una media de p ₀... y una desviación estándar de

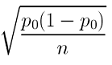
Este resultado proporciona la justificación teórica para construir el estadístico de prueba de la manera que lo hicimos, y por lo tanto los supuestos bajo los que se sostiene este resultado (en negrita, arriba) son las condiciones que nuestros datos necesitan satisfacer para que podamos usar esta prueba. Estas dos condiciones son:

i. La muestra tiene que ser aleatoria.

ii. Se cumplen las condiciones en las que la distribución muestral de p-hat es normal. En otras palabras:

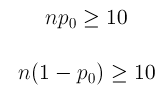
• Aquí haremos una pausa para decir más sobre la condición (i.) anterior, la necesidad de una muestra aleatoria. En la Unidad de Probabilidad se discutieron planes de muestreo basados en la probabilidad (como una muestra aleatoria simple, agrupamiento o muestreo estratificado) que producen una muestra no sesgada, la cual puede ser utilizada de manera segura para hacer inferencias sobre una población. Observamos en la Unidad de Probabilidad que, en la práctica, a veces se utilizan otras técnicas de muestreo (no aleatorias) cuando el muestreo aleatorio no es factible. Sin embargo, es importante, cuando se utilizan estas técnicas, conocer el tipo de sesgo que introducen, y así las limitaciones de las conclusiones que pueden extraerse de ellas. Para nuestro propósito aquí, nos centraremos en una de esas prácticas, la situación en la que una muestra no se elige realmente al azar, sino que en el contexto de la variable categórica que se está estudiando, la muestra se considera aleatoria. Por ejemplo, digamos que te interesa la proporción de alumnos de una determinada universidad que sufren de alergias estacionales. Para ello, los alumnos de una gran clase de ingeniería podrían considerarse como una muestra aleatoria, ya que no hay nada en estar en una clase de ingeniería que te haga más o menos propenso a sufrir alergias estacionales. Técnicamente, la clase de ingeniería es una muestra de conveniencia, pero se trata como una muestra aleatoria en el contexto de esta variable categórica. Por otro lado, si te interesa la proporción de estudiantes en la universidad que tienen ansiedad matemática, entonces la clase de estudiantes de ingeniería claramente no podría verse como una muestra aleatoria, ya que los estudiantes de ingeniería probablemente tienen una incidencia mucho menor de ansiedad matemática que la población universitaria en general.

Aprende haciendo: Proporciones (Paso 2) ¿Muestreo válido o inválido?

Comprobemos las condiciones en nuestros tres ejemplos.

EJEMPLO:

¿Se ha reducido la proporción de productos defectuosos como consecuencia de la reparación?

i. Los 400 productos fueron elegidos al azar.

ii. n = 400, p ₀ = 0.2 y por lo tanto:

\(n p_{0}=400(0.2)=80 \geq 10\)

\(n\left(1-p_{0}\right)=400(1-0.2)=320 \geq 10\)

EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

i. Los 100 alumnos fueron elegidos al azar.

ii. n = 100, p ₀ = 0.157 y por lo tanto:

\ begin {reunió}
n p_ {0} =100 (0.157) =15.7\ geq 10\\
n\ izquierda (1-p_ {0}\ derecha) =100 (1-0.157) =84.3\ geq 10
\ end {reunidos}

EJEMPLO:

¿La proporción de adultos estadounidenses que apoyan la pena de muerte cambió entre 2003 y una encuesta posterior?

i. Los 1000 adultos fueron elegidos al azar.

ii. n = 1000, p ₀ = 0.64 y por lo tanto:

\ begin {reunió}
n p_ {0} =1000 (0.64) =640\ geq 10\\
n\ izquierda (1-p_ {0}\ derecha) =1000 (1-0.64) =360\ geq 10
\ end {reunidos}

Aprende haciendo: Proporciones (Paso 2) Verificar Condiciones

Comprobar que nuestros datos satisfacen las condiciones bajo las cuales la prueba puede ser utilizada de manera confiable es una parte muy importante del proceso de prueba de hipótesis. Asegúrese de considerar esto para cada prueba de hipótesis que realice en este curso y ciertamente en la práctica.

Los cuatro pasos en las pruebas de hipótesis

• PASO 1: Indicar las hipótesis nulas y alternativas apropiadas, Ho y Ha.
• PASO 2: Obtener una muestra aleatoria, recopilar datos relevantes y verificar si los datos cumplen con las condiciones bajo las cuales se puede usar la prueba. Si se cumplen las condiciones, resumir los datos utilizando un estadístico de prueba.
• PASO 3: Encuentra el valor p de la prueba.
• PASO 4: Con base en el valor p, decida si los resultados son estadísticamente significativos o no y saque sus conclusiones en contexto.
• Nota: En la práctica, siempre debemos considerar la significación práctica de los resultados así como la significancia estadística.

Con respecto a la prueba z, la proporción poblacional que estamos discutiendo actualmente tenemos:

Paso 1: Finalizado

Paso 2: Finalizado

Paso 3: Esto es en lo que vamos a trabajar a continuación.

Proporciones (Paso 3)

CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.

Objetivos de aprendizaje

LO 4.33: En un contexto dado, distinguir entre situaciones que involucran una proporción poblacional y una media poblacional y especificar la hipótesis nula y alternativa correcta para el escenario.

Objetivos de aprendizaje

LO 4.34: Realizar una prueba de hipótesis completa para una proporción poblacional a mano.

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Objetivos de aprendizaje

LO 6.27: Explique qué es el valor p y cómo se utiliza para sacar conclusiones.

Video

Video: Proporciones (Paso 3) (14:46)

Calculadoras y Tablas

Paso 3. Encontrar el valor P de la prueba

Hasta ahora hemos hablado del valor p a nivel intuitivo: entender qué es (o qué mide) y cómo lo usamos para sacar conclusiones sobre la significación estadística de nuestros resultados. Ahora vamos a profundizar más en cómo se calcula el valor p.

Cabe mencionar que eventualmente confiaremos en la tecnología para calcular el valor p por nosotros (así como la estadística de prueba), pero para hacer un uso inteligente de la salida, es importante primero entender los detalles, y sólo entonces dejar que la computadora haga los cálculos por nosotros. Nuevamente, nuestro objetivo es usar este sencillo ejemplo para darte las herramientas que necesitas para entender completamente el proceso. Empecemos.

Recordemos que hasta el momento hemos dicho que el valor p es la probabilidad de obtener datos como los observados asumiendo que Ho es cierto. Al igual que el estadístico de prueba, el valor p es, por lo tanto, una medida de la evidencia contra Ho. En el caso del estadístico de prueba, cuanto mayor sea en magnitud (positiva o negativa), más p-hat es de p ₀, más evidencia tenemos contra Ho. En el caso del valor p, es lo contrario; cuanto más pequeño es, más improbable es obtener datos como los observados cuando Ho es cierto, más evidencia es contra Ho. De hecho, uno puede sacar conclusiones en las pruebas de hipótesis con solo usar el estadístico de prueba, y como veremos el valor p es, en cierto sentido, solo otra forma de ver el estadístico de prueba. La razón por la que realmente damos el paso extra en este curso y derivamos el valor p del estadístico de prueba es que aunque en este caso (la prueba sobre la proporción poblacional) y algunas otras pruebas, el valor del estadístico de prueba tiene una interpretación muy clara e intuitiva, hay algunas pruebas donde su valor no es tan fácil de interpretar. Por otro lado, el valor p mantiene su atractivo intuitivo en todas las pruebas estadísticas.

¿Cómo se calcula el valor p?

Intuitivamente, el valor p es la probabilidad de observar datos como los observados asumiendo que Ho es cierto. Seamos un poco más formales:

• Dado que esta es una pregunta de probabilidad sobre los datos, tiene sentido que el cálculo implique el resumen de datos, el estadístico de prueba.
• ¿Qué queremos decir con “como” los observados? Por “me gusta” nos referimos a “como extremo o incluso más extremo”.

Poniéndolo todo junto, lo conseguimos en general:

El valor p es la probabilidad de observar un estadístico de prueba tan extremo como el observado (o incluso más extremo) asumiendo que la hipótesis nula es verdadera.

Por “extremo” nos referimos a extremo en la (s) dirección (s) de la hipótesis alternativa.

Específicamente, para la prueba z para la proporción poblacional:

1. Si la hipótesis alternativa es Ha: p < p ₀ (menor que), entonces “extremo” significa pequeño o menor que, y el valor p es: La probabilidad de observar un estadístico de prueba tan pequeño como el observado o menor si la hipótesis nula es verdadera.
2. Si la hipótesis alternativa es Ha: p > p ₀ (mayor que), entonces “extremo” significa grande o mayor que, y el valor p es: La probabilidad de observar un estadístico de prueba tan grande como el observado o mayor si la hipótesis nula es verdadera.
3. Si la alternativa es Ha: p ≠ p ₀ (diferente de), entonces “extremo” significa extremo en cualquier dirección ya sea pequeño o grande (es decir, grande en magnitud) o simplemente diferente de, y el valor p por lo tanto es: La probabilidad de observar un estadístico de prueba tan grande en magnitud como la observada o mayor si la hipótesis nula es verdadera. (Ejemplos: Si z = -2.5: valor p = probabilidad de observar un estadístico de prueba tan pequeño como -2.5 o menor o tan grande como 2.5 o mayor. Si z = 1.5: valor p = probabilidad de observar un estadístico de prueba tan grande como 1.5 o mayor, o tan pequeño como -1.5 o menor.)

Bien, ojalá eso tenga (algún) sentido. Pero, ¿cómo lo calculamos realmente?

Recordemos el importante comentario de nuestra discusión sobre nuestra estadística de prueba,

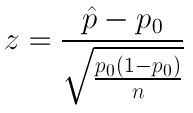
que decía que cuando la hipótesis nula es verdadera (es decir, cuando p = p ₀), los posibles valores de nuestro estadístico de prueba siguen una distribución normal estándar (N (0,1), denotada por Z). Por lo tanto, los cálculos del valor p (que asumen que Ho es verdadero) son simplemente cálculos de distribución normal estándar para las 3 posibles hipótesis alternativas.

La hipótesis alternativa es “menor que”

La probabilidad de observar un estadístico de prueba tan pequeño como el observado o menor, asumiendo que los valores del estadístico de prueba siguen una distribución normal estándar. Ahora representaremos esta probabilidad en símbolos y también usando la distribución normal.

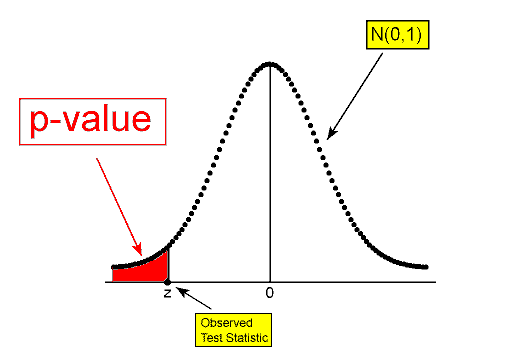
Al observar la región sombreada, puede ver por qué esto a menudo se conoce como una prueba de cola izquierda. Nos sombreamos a la izquierda del estadístico de prueba, ya que menos de lo que está a la izquierda.

La hipótesis alternativa es “mayor que”

La probabilidad de observar un estadístico de prueba tan grande como el observado o mayor, asumiendo que los valores del estadístico de prueba siguen una distribución normal estándar. Nuevamente, representaremos esta probabilidad en símbolos y usando la distribución normal

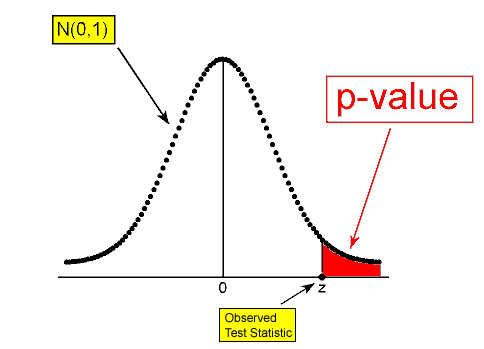
Al observar la región sombreada, puede ver por qué esto a menudo se conoce como una prueba de cola derecha. Nos sombreamos a la derecha del estadístico de prueba, ya que mayor que está a la derecha.

La hipótesis alternativa es “no igual a”

La probabilidad de observar un estadístico de prueba que es tan grande en magnitud como la observada o mayor, asumiendo que los valores del estadístico de prueba siguen una distribución normal estándar.

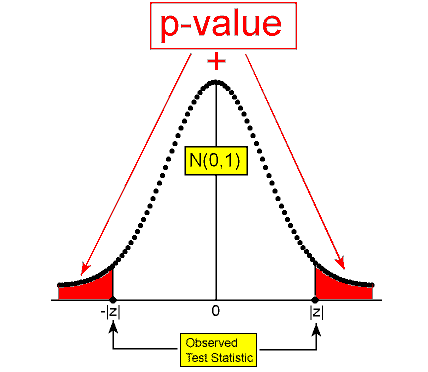
Esto a menudo se conoce como una prueba de dos colas, ya que sombreamos en ambas direcciones.

A continuación, aplicaremos esto a nuestros tres ejemplos. Pero primero, trabaja a través de las siguientes actividades, que deberían ayudar a tu comprensión.

Aprender haciendo: Proporciones (Paso 3)

¿Conseguí esto? : Proporciones (Paso 3)

EJEMPLO:

¿Se ha reducido la proporción de productos defectuosos como consecuencia de la reparación?

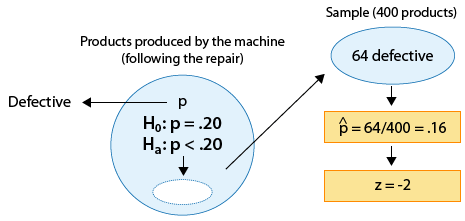
El valor p en este caso es:

• La probabilidad de observar un estadístico de prueba tan pequeño como -2 o menor, asumiendo que Ho es cierto.

O (recordando lo que realmente significa el estadístico de prueba en este caso),

• La probabilidad de observar una proporción muestral que es 2 desviaciones estándar o más por debajo del valor nulo (p ₀ = 0.20), asumiendo que p ₀ es la verdadera proporción poblacional.

O, más específicamente,

• La probabilidad de observar una proporción muestral de 0.16 o menor en una muestra aleatoria de tamaño 400, cuando la verdadera proporción poblacional es p ₀ =0.20

En cualquier caso, el valor p se encuentra como se muestra en la siguiente figura:

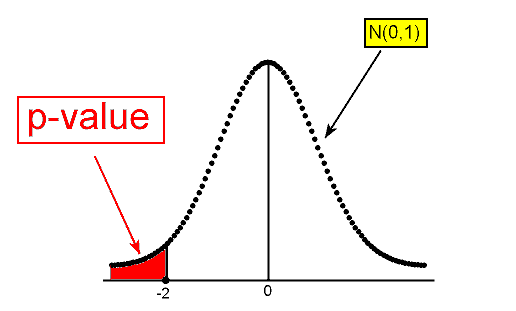
Para encontrar P (Z ≤ -2) podemos usar la calculadora o tabla que aprendimos a usar en la unidad de probabilidad para variables aleatorias normales. Eventualmente, después de entender los detalles, usaremos software para ejecutar la prueba por nosotros y la salida nos dará toda la información que necesitamos. El valor p que proporciona el software estadístico para este ejemplo específico es 0.023. El valor p nos dice que es bastante improbable (probabilidad de 0.023) obtener datos como los observados (estadística de prueba de -2 o menos) asumiendo que Ho es cierto.

EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

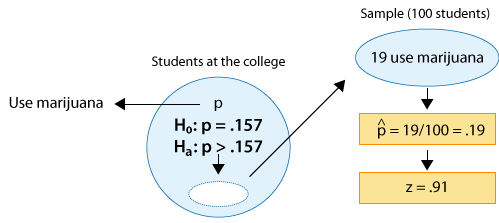
El valor p en este caso es:

• La probabilidad de observar un estadístico de prueba tan grande como 0.91 o mayor, asumiendo que Ho es cierto.

O (recordando lo que realmente significa el estadístico de prueba en este caso),

• La probabilidad de observar una proporción muestral que es 0.91 desviaciones estándar o más por encima del valor nulo (p ₀ = 0.157), asumiendo que p ₀ es la verdadera proporción poblacional.

O, más específicamente,

• La probabilidad de observar una proporción muestral de 0.19 o superior en una muestra aleatoria de tamaño 100, cuando la verdadera proporción poblacional es p ₀ =0.157

En cualquier caso, el valor p se encuentra como se muestra en la siguiente figura:

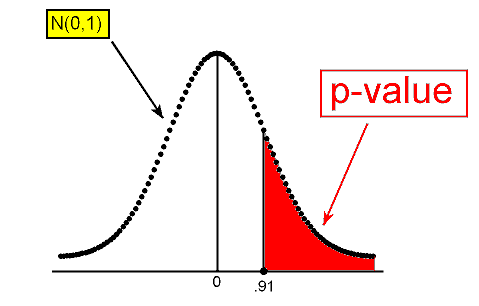
Nuevamente, en este punto podemos usar la calculadora o tabla para encontrar que el valor p es 0.182, esto es P (Z ≥ 0.91).

El valor p nos dice que no es muy sorprendente (probabilidad de 0.182) obtener datos como los observados (que arrojan un estadístico de prueba de 0.91 o superior) asumiendo que la hipótesis nula es verdadera.

EJEMPLO:

¿La proporción de adultos estadounidenses que apoyan la pena de muerte cambió entre 2003 y una encuesta posterior?

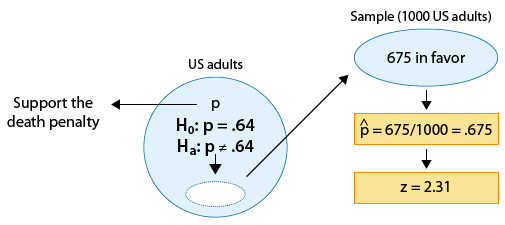
El valor p en este caso es:

• La probabilidad de observar un estadístico de prueba tan grande como 2.31 (o mayor) o tan pequeño como -2.31 (o menor), asumiendo que Ho es cierto.

O (recordando lo que realmente significa el estadístico de prueba en este caso),

• La probabilidad de observar una proporción muestral que es 2.31 desviaciones estándar o más alejada del valor nulo (p ₀ = 0.64), asumiendo que p ₀ es la verdadera proporción poblacional.

O, más específicamente,

• La probabilidad de observar una proporción muestral tan diferente como 0.675 es de 0.64, o incluso más diferente (es decir, tan alta como 0.675 o superior o tan baja como 0.605 o menor) en una muestra aleatoria de tamaño 1,000, cuando la verdadera proporción poblacional es p ₀ = 0.64

En cualquier caso, el valor p se encuentra como se muestra en la siguiente figura:

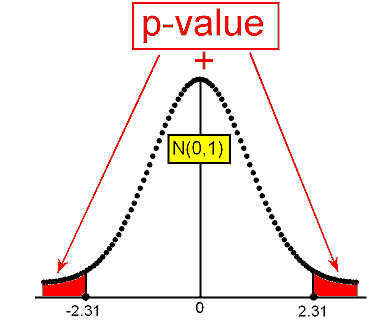
Nuevamente, en este punto podemos usar la calculadora o tabla para encontrar que el valor p es 0.021, esto es P (Z ≤ -2.31) + P (Z ≥ 2.31) = 2*P (Z ≥ |2.31|)

El valor p nos dice que es bastante improbable (probabilidad de 0.021) obtener datos como los observados (estadístico de prueba tan alto como 2.31 o superior o tan bajo como -2.31 o menor) asumiendo que Ho es cierto.

Comentario:

• Acabamos de ver que encontrar valores p implica cálculos de probabilidad sobre el valor del estadístico de prueba asumiendo que Ho es cierto. En este caso, cuando Ho es verdadero, los valores del estadístico de prueba siguen una distribución normal estándar (es decir, la distribución de muestreo del estadístico de prueba cuando la hipótesis nula es verdadera es N (0,1)). Por lo tanto, los valores p corresponden a áreas (probabilidades) bajo la curva normal estándar.

De igual manera, en cualquier prueba, los valores p se encuentran utilizando la distribución de muestreo del estadístico de prueba cuando la hipótesis nula es verdadera (también conocida como la “distribución nula” del estadístico de prueba). En este caso, fue relativamente fácil argumentar que la distribución nula de nuestro estadístico de prueba es N (0,1). Como veremos, en otras pruebas surgen otras distribuciones (como la distribución t y la distribución F), que solo mencionaremos brevemente, y confiamos en gran medida en la salida de nuestro paquete estadístico para obtener los valores p.

Acabamos de terminar nuestra discusión sobre el valor p, y cómo se calcula tanto en general como más específicamente para la prueba z para la proporción poblacional. Volvamos al proceso de cuatro pasos de las pruebas de hipótesis y veamos qué hemos cubierto y qué es lo que aún hay que discutir.

Los cuatro pasos en las pruebas de hipótesis

• PASO 1: Indicar las hipótesis nulas y alternativas apropiadas, Ho y Ha.

• PASO 2: Obtener una muestra aleatoria, recopilar datos relevantes y verificar si los datos cumplen con las condiciones bajo las cuales se puede usar la prueba. Si se cumplen las condiciones, resumir los datos utilizando un estadístico de prueba.

• PASO 3: Encuentra el valor p de la prueba.

• PASO 4: Con base en el valor p, decida si los resultados son estadísticamente significativos o no y saque sus conclusiones en contexto.

• Nota: En la práctica, siempre debemos considerar la significación práctica de los resultados así como la significancia estadística.

Con respecto a la prueba z la proporción poblacional:

Paso 1: Finalizado

Paso 2: Finalizado

Paso 3: Finalizado

Paso 4. Esto es en lo que vamos a trabajar a continuación.

Aprender haciendo: Proporciones (Paso 3) Comprensión de los valores P

Proporciones (Paso 4 y Resumen)

CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.

Objetivos de aprendizaje

LO 4.33: En un contexto dado, distinguir entre situaciones que involucran una proporción poblacional y una media poblacional y especificar la hipótesis nula y alternativa correcta para el escenario.

Objetivos de aprendizaje

LO 4.34: Realizar una prueba de hipótesis completa para una proporción poblacional a mano.

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Objetivos de aprendizaje

LO 6.27: Explique qué es el valor p y cómo se utiliza para sacar conclusiones.

Video

Video: Proporciones (Paso 4 y Resumen) (4:30)

Paso 4. Dibujo de conclusiones basadas en el valor P

Esta última parte del proceso de cuatro pasos de las pruebas de hipótesis es la misma en todas las pruebas estadísticas, y en realidad, ya hemos dicho básicamente todo lo que hay que decir al respecto, pero no puede hacer daño volver a decirlo.

El valor p es una medida de cuánta evidencia presentan los datos contra Ho. Cuanto menor es el valor p, más evidencia presentan los datos contra Ho.

Ya mencionamos que lo que determina lo que constituye evidencia suficiente contra Ho es el nivel de significancia (α, alfa), un punto de corte por debajo del cual el valor p se considera lo suficientemente pequeño como para rechazar a Ho a favor de Ha. El nivel de significancia más utilizado es 0.05.

• Si el valor p ≤ 0.05 entonces RECHAZAMOS Ho
  • Conclusión: HAY suficiente evidencia de que Ha es Verdadero
• Si el valor p > 0.05 entonces FALLAMOS EN RECHAZAR Ho
  • Conclusión: NO HAY suficiente evidencia de que Ha es Verdadero

Donde en lugar de Ha es Verdadero, escribimos lo que esto significa en palabras del problema, es decir, en el contexto del escenario actual.

Es importante mencionar nuevamente que este paso tiene esencialmente dos sub-pasos:

• (i) Con base en el valor p, determinar si los resultados son o no estadísticamente significativos (es decir, los datos presentan evidencia suficiente para rechazar Ho).
• ii) Exponga sus conclusiones en el contexto del problema.

Nota: Siempre debemos considerar si los resultados tienen algún significado práctico, particularmente si son estadísticamente significativos como un resultado estadísticamente significativo que no tiene uso práctico es esencialmente sin sentido!

Volvamos a nuestros tres ejemplos y saquemos conclusiones.

EJEMPLO:

¿Se ha reducido la proporción de productos defectuosos como consecuencia de la reparación?

Encontramos que el valor p para esta prueba fue 0.023.

Dado que 0.023 es pequeño (en particular, 0.023 < 0.05), los datos proporcionan evidencia suficiente para rechazar Ho.

Conclusión:

• Hay suficiente evidencia de que la proporción de productos defectuosos es menor al 20% después de la reparación.

La siguiente figura es la historia completa de este ejemplo, e incluye todos los pasos por los que pasamos, comenzando por exponer las hipótesis y terminando con nuestras conclusiones:

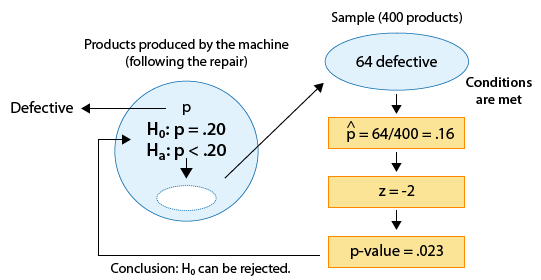
EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

Encontramos que el valor p para esta prueba fue 0.182.

Dado que .182 no es pequeño (en particular, 0.182 > 0.05), los datos no aportan pruebas suficientes para rechazar a Ho.

Conclusión:

• NO HAY pruebas suficientes de que la proporción de estudiantes de la universidad que consumen mariguana sea superior a la cifra nacional.

Aquí está la historia completa de este ejemplo:

.157. Tomamos una muestra de 100 alumnos, representados por un círculo más pequeño. Encontramos que 19 usan marihuana. p-hat = 19/100 = .19, z = .91, y p-valor = .182. Dado que el valor p es demasiado grande concluimos que H_0 no puede ser rechazado.” height="278" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...3/image276.gif "title="Un círculo grande representa a la población Estudiantes en la universidad. Queremos saber p sobre esta población, o cuál es la proporción poblacional de estudiantes que consumen marihuana. Las hipótesis son H_0: p = .157 y H_a: p > .157. Tomamos una muestra de 100 alumnos, representados por un círculo más pequeño. Encontramos que 19 usan marihuana. p-hat = 19/100 = .19, z = .91, y p-valor = .182. Como el valor p es demasiado grande concluimos que H_0 no puede ser rechazado.” width="564">

Aprender haciendo: aprender haciendo — proporciones (Paso 4)

EJEMPLO:

¿La proporción de adultos estadounidenses que apoyan la pena de muerte cambió entre 2003 y una encuesta posterior?

Encontramos que el valor p para esta prueba fue 0.021.

Dado que 0.021 es pequeño (en particular, 0.021 < 0.05), los datos proporcionan suficiente evidencia para rechazar Ho

Conclusión:

• HAY pruebas suficientes de que la proporción de adultos que apoyan la pena de muerte para asesinos condenados ha cambiado desde 2003.

Aquí está la historia completa de este ejemplo:

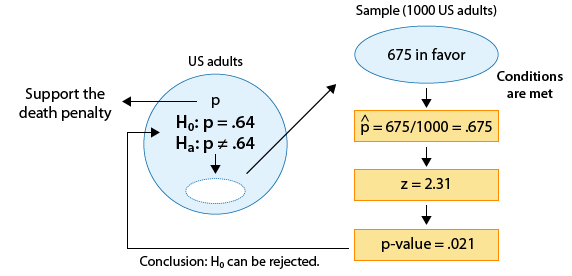
¿Conseguí esto? : Proporciones (Paso 4)

Muchos estudiantes se preguntan: pruebas de hipótesis para la proporción poblacional

Muchos estudiantes se preguntan por qué el 5% a menudo se selecciona como el nivel de significancia en las pruebas de hipótesis, y por qué 1% es el siguiente nivel más típico. Esto se debe en gran parte a la conveniencia y la tradición.

Cuando Ronald Fisher (uno de los fundadores de la estadística moderna) publicó una de sus tablas, utilizó una escala matemáticamente conveniente que incluía 5% y 1%. Posteriormente, estos mismos niveles de 5% y 1% fueron utilizados por otras personas, en parte solo porque Fisher era muy estimado. Pero sobre todo estos son niveles arbitrarios.

La idea de seleccionar algún tipo de punto de corte relativamente pequeño fue históricamente importante en el desarrollo de la estadística; pero es importante recordar que realmente existe un rango continuo de confianza creciente hacia la hipótesis alternativa, no un solo valor de todo o nada. No hay mucha diferencia significativa, por ejemplo, entre un valor p de .049 o .051, y sería una tontería declarar definitivamente un caso un efecto “real” y declarar el otro caso definitivamente un efecto “aleatorio”. En cualquier caso, los resultados del estudio fueron aproximadamente 5% probables por casualidad si no hay ningún efecto real.

Si tal valor p es suficiente para rechazar una hipótesis nula particular depende en última instancia del riesgo de tomar una decisión equivocada, y de la medida en que el efecto hipotético pueda contradecir nuestra experiencia previa o estudios previos.

Resumimos!!

Ya hemos terminado de pasar por los cuatro pasos de las pruebas de hipótesis, y en particular aprendimos cómo se aplican a la prueba z para la proporción poblacional. Aquí hay un breve resumen:

• Paso 1: Exponer las hipótesis

Afirma la hipótesis nula:

Ho: p = p ₀

Exponer la hipótesis alternativa:

Ha: p < p ₀ (unilateral)

Ha: p > p ₀ (unilateral)

Ha: p ≠ p ₀ (bilateral)

donde la elección de la alternativa apropiada (de las tres) suele ser bastante clara desde el contexto del problema. Si sientes que no está claro, lo más probable es que sea un problema de dos caras. Los estudiantes suelen ser buenos para reconocer la terminología “más que” y “menos que” pero las diferencias a veces pueden ser más difíciles de detectar, a veces esto se debe a que tienes ideas preconcebidas de cómo crees que debería ser! Utilice solo la información dada en el problema.

• Paso 2: Obtener datos, verificar condiciones y resumir datos

Obtener datos de una muestra y:

(i) Comprobar si los datos cumplen las condiciones que le permiten utilizar esta prueba.

muestra aleatoria (o al menos una muestra que puede considerarse aleatoria en contexto)

se cumplen las condiciones en las que la distribución muestral de p-hat es normal

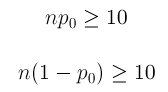
(ii) Calcular la proporción muestral p-hat, y resumir los datos utilizando el estadístico de prueba:

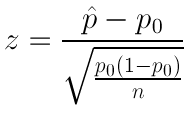
(Recordemos: Este estadístico de prueba estandarizado representa cuántas desviaciones estándar por encima o por debajo de p ₀ es nuestra proporción muestral p-hat.)

• Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera

HECHO IMPORTANTE: En todas las pruebas futuras, confiaremos en el software para obtener el valor p.

Cuando la hipótesis alternativa es “menor que” la probabilidad de observar un estadístico de prueba tan pequeño como el observado o menor, asumiendo que los valores del estadístico de prueba siguen una distribución normal estándar. Ahora representaremos esta probabilidad en símbolos y también usando la distribución normal.

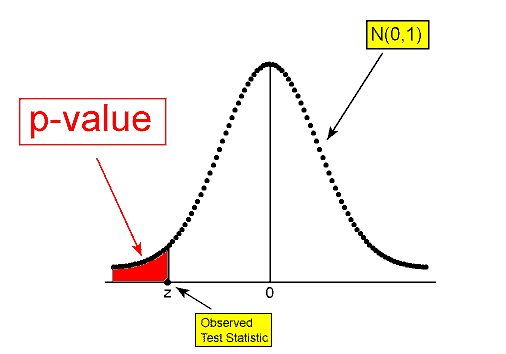
Al observar la región sombreada, puede ver por qué esto a menudo se conoce como una prueba de cola izquierda. Nos sombreamos a la izquierda del estadístico de prueba, ya que menos de lo que está a la izquierda.

Cuando la hipótesis alternativa es “mayor que” la probabilidad de observar un estadístico de prueba tan grande como el observado o mayor, asumiendo que los valores del estadístico de prueba siguen una distribución normal estándar. Nuevamente, representaremos esta probabilidad en símbolos y usando la distribución normal

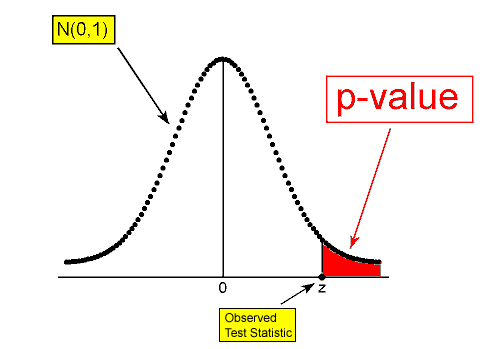
Al observar la región sombreada, puede ver por qué esto a menudo se conoce como una prueba de cola derecha. Nos sombreamos a la derecha del estadístico de prueba, ya que mayor que está a la derecha.

Cuando la hipótesis alternativa es “no igual a” la probabilidad de observar un estadístico de prueba que es tan grande en magnitud como la observada o mayor, asumiendo que los valores del estadístico de prueba siguen una distribución normal estándar.

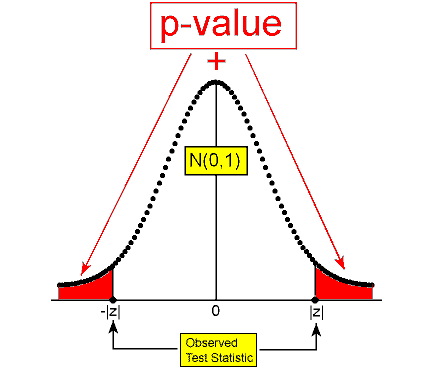
Esto a menudo se conoce como una prueba de dos colas, ya que sombreamos en ambas direcciones.

• Paso 4: Conclusión

Llegar primero a una conclusión sobre la significancia estadística de los resultados, y luego determinar qué significa en el contexto del problema.

Si el valor p ≤ 0.05 entonces
RECHAZAMOS Ho Conclusión: Hay suficiente evidencia de que Ha es Verdadero

Si el valor p > 0.05 entonces NO RECHAMOS EN RECHAZAR Ho
Conclusión: NO HAY suficiente evidencia de que Ha es Verdadero

Recordemos que: Si el valor p es pequeño (en particular, menor que el nivel de significancia, que suele ser 0.05), los resultados son estadísticamente significativos (en el sentido de que existe una diferencia estadísticamente significativa entre lo observado en la muestra y lo reclamado en Ho), y así rechazamos Ho.

Si el valor p no es pequeño, no tenemos evidencia estadística suficiente para rechazar a Ho, y así seguimos creyendo que Ho puede ser cierto. (Recuerda: En las pruebas de hipótesis nunca “aceptamos” a Ho).

Finalmente, en la práctica, siempre debemos considerar la significación práctica de los resultados así como la significancia estadística.

Aprende haciendo: Prueba Z para una proporción poblacional

¿Cuál es el siguiente?

Antes de pasar a la siguiente prueba, vamos a utilizar la prueba z para proporciones para plantear e ilustrar algunos temas más muy importantes respecto a las pruebas de hipótesis. Este también podría ser un buen momento para revisar los conceptos de error tipo I, error tipo II y potencia antes de continuar.

Más sobre Hypothesis Testing

CO-1: Describir los roles que la bioestadística desempeña en la disciplina de la salud pública.

Objetivos de aprendizaje

LO 1.11: Reconocer la distinción entre significancia estadística y significación práctica.

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Objetivos de aprendizaje

LO 6.30: Utilizar un intervalo de confianza para determinar la conclusión correcta de la prueba de hipótesis bilateral asociada.

Video

Video: Más sobre las Pruebas de Hipótesis (18:25)

Las cuestiones relativas a las pruebas de hipótesis que discutiremos son:

1. El efecto del tamaño de la muestra en las pruebas de hipótesis.
2. Significancia estadística vs. importancia práctica.
3. Pruebas de hipótesis e intervalos de confianza: ¿cómo se relacionan?

Empecemos.

1. El efecto del tamaño de la muestra en las pruebas de hipótesis

Ya hemos visto el efecto que el tamaño muestral tiene sobre la inferencia, cuando discutimos la estimación de punto e intervalo para la media poblacional (μ, mu) y la proporción poblacional (p). Intuitivamente...

Los tamaños de muestra más grandes nos dan más información para precisar la verdadera naturaleza de la población. Por lo tanto, podemos esperar que la media muestral y la proporción muestral obtenida de una muestra más grande estén más cerca de la media y proporción de la población, respectivamente. Como resultado, para el mismo nivel de confianza, podemos reportar un margen de error más pequeño, y obtener un intervalo de confianza más estrecho. Lo que hemos visto, entonces, es que un tamaño de muestra más grande da un impulso a lo mucho que confiamos en nuestros resultados de muestra.

En las pruebas de hipótesis, los tamaños de muestra más grandes tienen un efecto similar. También hemos comentado que la potencia de nuestra prueba aumenta cuando aumenta el tamaño de la muestra, permaneciendo todo lo demás igual. Esto significa que tenemos una mejor oportunidad de detectar la diferencia entre el valor verdadero y el valor nulo para muestras más grandes.

Los siguientes dos ejemplos ilustrarán que un tamaño de muestra más grande proporciona evidencia más convincente (la prueba tiene mayor poder), y cómo la evidencia se manifiesta en las pruebas de hipótesis. Volvamos a nuestro ejemplo 2 (consumo de marihuana en cierta universidad de artes liberales).

EJEMPLO:

¿La proporción de consumidores de marihuana en la universidad es mayor que la cifra nacional?

.157. Tomamos una muestra de 100 alumnos, representados por un círculo más pequeño. Encontramos que 19 usan marihuana. p-hat = 19/100 = .19, z = .91, y p-valor = .182. Dado que el valor p es demasiado grande concluimos que H_0 no puede ser rechazado.” height="278" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...3/image276.gif "title="Un círculo grande representa a la población Estudiantes en la universidad. Queremos saber p sobre esta población, o cuál es la proporción poblacional de estudiantes que consumen marihuana. Las hipótesis son H_0: p = .157 y H_a: p > .157. Tomamos una muestra de 100 alumnos, representados por un círculo más pequeño. Encontramos que 19 usan marihuana. p-hat = 19/100 = .19, z = .91, y p-valor = .182. Como el valor p es demasiado grande concluimos que H_0 no puede ser rechazado.” width="564">

No contamos con pruebas suficientes para concluir que la proporción de estudiantes de la universidad que consumen mariguana es superior a la cifra nacional.

---

Ahora, aumentemos el tamaño de la muestra.

Hay rumores de que los estudiantes de cierta universidad de artes liberales están más inclinados a consumir drogas que los universitarios estadounidenses en general. Supongamos que en una simple muestra aleatoria de 400 alumnos del colegio, 76 admitieron el consumo de mariguana. ¿Los datos proporcionan evidencia suficiente para concluir que la proporción de consumidores de marihuana entre los estudiantes de la universidad (p) es mayor que la proporción nacional, que es 0.157? (Reportado por la Escuela de Salud Pública de Harvard).

.157. Tomamos una muestra de 400 estudiantes, representados por un círculo más pequeño, y encontramos que 76 consumen marihuana. Se cumplen las condiciones para utilizar nuestro método, por lo que p-hat = 76/400 = .19, z = 1.81, y p-value = .035. El valor p es lo suficientemente bajo como para concluir que podemos rechazar H_0.” height="292" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...3/image291.gif "title="Un círculo grande representa a la población Estudiantes en la universidad. Queremos saber p sobre esta población, o cuál es la proporción poblacional de estudiantes que consumen marihuana. Las hipótesis son H_0: p = .157 y H_a: p > .157. Tomamos una muestra de 400 estudiantes, representados por un círculo más pequeño, y encontramos que 76 consumen marihuana. Se cumplen las condiciones para utilizar nuestro método, por lo que p-hat = 76/400 = .19, z = 1.81, y p-value = .035. El valor p es lo suficientemente bajo como para concluir que podemos rechazar H_0.” width="572">

Nuestros resultados aquí son estadísticamente significativos. Es decir, en el ejemplo 2* los datos aportan pruebas suficientes para rechazar a Ho.

• Conclusión: Existe suficiente evidencia de que la proporción de consumidores de marihuana en la universidad es mayor que entre todos los estudiantes estadounidenses.

¿Qué aprendemos de esto?

Vemos que los resultados de la muestra que se basan en una muestra más grande llevan más peso (tienen mayor potencia).

En el ejemplo 2, vimos que una proporción muestral de 0.19 basada en una muestra de tamaño de 100 no fue suficiente evidencia de que la proporción de consumidores de marihuana en la universidad sea superior a 0.157. Recordemos, de nuestra visión general de las pruebas de hipótesis, que esta conclusión (no tener suficiente evidencia para rechazar la hipótesis nula) no significa que la hipótesis nula sea necesariamente cierta (entonces, nunca “aceptamos” lo nulo); solo significa que el estudio particular no arrojó evidencia suficiente para rechazar el nulo. Podría ser que el tamaño de la muestra era simplemente demasiado pequeño para detectar una diferencia estadísticamente significativa.

No obstante, en el ejemplo 2*, vimos que cuando se obtiene la proporción muestral de 0.19 de una muestra de talla 400, ésta lleva mucho más peso, y en particular, aporta pruebas suficientes de que la proporción de consumidores de marihuana en el colegio es superior a 0.157 (la cifra nacional). En este caso, el tamaño muestral de 400 fue lo suficientemente grande como para detectar una diferencia estadísticamente significativa.

La siguiente actividad te permitirá practicar las ideas y terminología utilizadas en las pruebas de hipótesis cuando un resultado no sea estadísticamente significativo.

Aprender haciendo: Interpretar resultados no significativos

2. Significancia estadística vs. importancia práctica.

Ahora, abordaremos el tema de significancia estadística versus importancia práctica (que también involucra cuestiones de tamaño muestral).

La siguiente actividad le permitirá explorar el efecto del tamaño de la muestra en la significancia estadística de los resultados usted mismo, y lo que es más importante, discutirá el tema 2: Significancia estadística vs. importancia práctica.

Dato importante: En general, con un tamaño de muestra suficientemente grande se puede hacer cualquier resultado que tenga muy poca importancia práctica estadísticamente significativo! Un gran tamaño de muestra por sí solo NO hace un “buen” estudio!!

Esto sugiere que al interpretar los resultados de una prueba, siempre se debe pensar no sólo en la significancia estadística de los resultados sino también en su importancia práctica.

Aprender haciendo: Significación estadística vs. práctica

3. Prueba de hipótesis e intervalos de confianza

El último tema que queremos discutir es la relación entre la prueba de hipótesis y los intervalos de confianza. Aunque el sabor de estas dos formas de inferencia es diferente (los intervalos de confianza estiman un parámetro, y las pruebas de hipótesis evalúan la evidencia en los datos contra una afirmación y a favor de otra), existe un fuerte vínculo entre ellas.

Explicaremos este vínculo (usando la prueba z y el intervalo de confianza para la proporción poblacional), y luego explicaremos cómo se pueden usar los intervalos de confianza después de que se haya realizado una prueba.

Recordemos que un intervalo de confianza nos da un conjunto de valores plausibles para el parámetro poblacional desconocido. Por lo tanto, podemos examinar un intervalo de confianza para decidir informalmente si un valor propuesto de proporción poblacional parece plausible.

Por ejemplo, si un intervalo de confianza del 95% para p, la proporción de todos los adultos estadounidenses ya familiarizados con Viagra en mayo de 1998, fue (0.61, 0.67), entonces parece claro que deberíamos poder rechazar una afirmación de que solo el 50% de todos los adultos estadounidenses estaban familiarizados con el medicamento, ya que con base en el intervalo de confianza, 0.50 es ni uno de los valores plausibles para p.

De hecho, la información proporcionada por un intervalo de confianza puede relacionarse formalmente con la información proporcionada por una prueba de hipótesis. (Comentario: La relación es más directa para las alternativas de dos caras, por lo que no presentaremos resultados para los casos unilaterales.)

Supongamos que queremos llevar a cabo la prueba bilateral:

• Ho: p = p ₀
• Ha: p ≠ p ₀

usando un nivel de significancia de 0.05.

Una forma alternativa de realizar esta prueba es encontrar un intervalo de confianza del 95% para p y verificar:

• Si p ₀ cae fuera del intervalo de confianza, rechace Ho.
• Si p ₀ cae dentro del intervalo de confianza, no rechace Ho.

En otras palabras,

• Si p ₀ no es uno de los valores plausibles para p, rechazamos Ho.
• Si p ₀ es un valor plausible para p, no podemos rechazar Ho.

(Comentario: Del mismo modo, los resultados de una prueba que utiliza un nivel de significancia de 0.01 pueden estar relacionados con el intervalo de confianza del 99%.)

Veamos un ejemplo:

EJEMPLO:

Recordemos el ejemplo 3, donde queríamos saber si la proporción de adultos estadounidenses que apoyan la pena de muerte para asesinos condenados ha cambiado desde 2003, cuando era de 0.64.

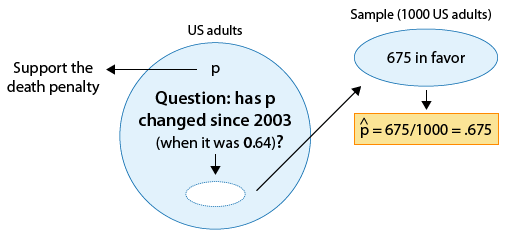
Estamos probando:

• Ho: p = 0.64 (Sin cambios desde 2003).
• Ha: p ≠ 0.64 (Algún cambio desde 2003).

y como nos recuerda la cifra, tomamos una muestra de mil adultos estadunidenses, y los datos nos dijeron que 675 apoyaban la pena de muerte para asesinos condenados (p-hat = 0.675).

Un intervalo de confianza del 95% para p, la proporción de todos los adultos estadounidenses que apoyan la pena de muerte, es:

\(0.675 \pm 1.96 \sqrt{\dfrac{0.675(1-0.675)}{1000}} \approx 0.675 \pm 0.029=(0.646,0.704)\)

Dado que el intervalo de confianza del 95% para p no incluye 0.64 como valor plausible para p, podemos rechazar Ho y concluir (como hicimos antes) que hay pruebas suficientes de que la proporción de adultos estadounidenses que apoyan la pena de muerte para asesinos condenados ha cambiado desde 2003.

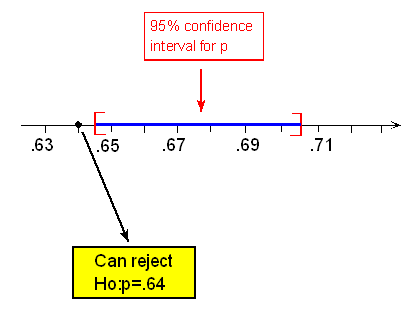
EJEMPLO:

Tú y tu compañero de cuarto están discutiendo sobre a quién le toca limpiar el departamento. Tu compañero de cuarto sugiere que resuelvas esto arrojando una moneda y saca una de una caja cerrada que tiene en la repisa. Sospechando que la moneda podría no ser justa, decides probarla primero. Tiras la moneda 80 veces, pensando para ti mismo que si, de hecho, la moneda es justa, deberías conseguir alrededor de 40 cabezas. En su lugar se obtienen 48 cabezas. Estás desconcertado. No está seguro de si sacar 48 cabezas de 80 es evidencia suficiente para concluir que la moneda está desequilibrada, o si este es un resultado que podría haber ocurrido solo por casualidad cuando la moneda es justa.

Las estadísticas pueden ayudarte a responder a esta pregunta.

Sea p la verdadera proporción (probabilidad) de cabezas. Queremos probar si la moneda es justa o no.

Estamos probando:

• Ho: p = 0.5 (la moneda es justa).
• Ha: p ≠ 0.5 (la moneda no es justa).

Los datos que tenemos son que de n = 80 tiradas, obtuvimos 48 cabezas, o que la proporción muestral de cabezas es p-hat = 48/80 = 0.6.

Un intervalo de confianza del 95% para p, la verdadera proporción de cabezas para esta moneda, es:

\(0.6 \pm 1.96 \sqrt{\dfrac{0.6(1-0.6)}{80}} \approx 0.6 \pm 0.11=(0.49,0.71)\)

Ya que en este caso 0.5 es uno de los valores plausibles para p, no podemos rechazar Ho. Es decir, los datos no aportan pruebas suficientes para concluir que la moneda no es justa.

Comentario

El contexto del último ejemplo es una buena oportunidad para sacar a colación un punto importante que se discutió anteriormente.

Aunque usamos 0.05 como punto de corte para guiar nuestra decisión sobre si los resultados son estadísticamente significativos, no debemos tratarlo como inviolable y siempre debemos agregar nuestro propio juicio. Volvamos a ver el último ejemplo.

Resulta que el valor p de esta prueba es de 0.0734. En otras palabras, tal vez no sea extremadamente improbable, pero es bastante improbable (probabilidad de 0.0734) que cuando lanzas una moneda justa 80 veces obtengas una proporción muestral de cabezas de 48/80 = 0.6 (o incluso más extrema). Es cierto que usando el nivel de significancia 0.05 (corte), 0.0734 no se considera lo suficientemente pequeño como para concluir que la moneda no es justa. Sin embargo, si realmente no quieres limpiar el departamento, el valor p podría ser lo suficientemente pequeño como para que le pidas a tu compañero de cuarto que use una moneda diferente, ¡o que te la proporcione tú mismo!

¿Conseguí esto? : Conexión entre intervalos de confianza y pruebas de hipótesis

¿Conseguí esto? : Pruebas de Hipótesis para Proporciones (Práctica Extra)

Aquí está nuestro último punto sobre este tema:

Cuando los datos proporcionan evidencia suficiente para rechazar Ho, podemos concluir (dependiendo de la hipótesis alternativa) que la proporción poblacional es menor que, mayor que, o no igual al valor nulo p ₀. Sin embargo, no obtenemos una declaración más informativa sobre su valor real. Podría ser de interés, entonces, seguir la prueba con un intervalo de confianza del 95% que nos dará más información sobre el valor real de p.

EJEMPLO:

En nuestro ejemplo 3,

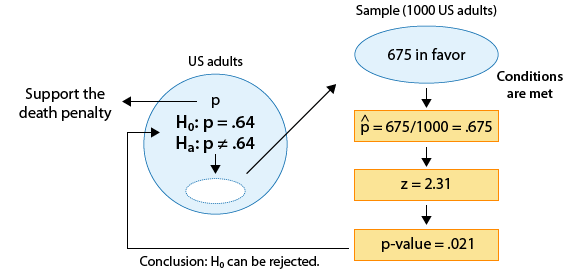
concluimos que la proporción de adultos estadounidenses que apoyan la pena de muerte para asesinos condenados ha cambiado desde 2003, cuando era de 0.64. Probablemente sea de interés no sólo saber que la proporción ha cambiado, sino también estimar a qué ha cambiado. Hemos calculado el intervalo de confianza del 95% para p en la página anterior y encontramos que es (0.646, 0.704).

Podemos combinar nuestras conclusiones de la prueba y el intervalo de confianza y decir:

Los datos proporcionan evidencia de que la proporción de adultos estadounidenses que apoyan la pena de muerte para asesinos condenados ha cambiado desde 2003, y estamos 95% seguros de que ahora está entre 0.646 y 0.704. (es decir, entre 64.6% y 70.4%).

EJEMPLO:

Veamos nuestro ejemplo 1 para ver cómo un intervalo de confianza después de una prueba puede ser perspicaz de una manera diferente.

Aquí hay un resumen del ejemplo 1:

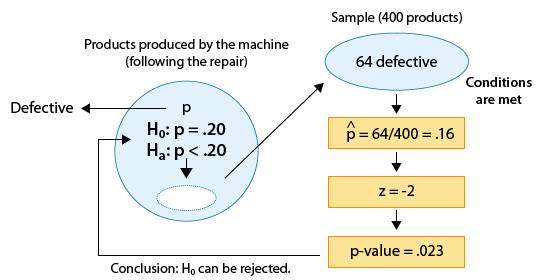
Se concluye que como resultado de la reparación, la proporción de productos defectuosos se ha reducido a menos de 0.20 (que fue la proporción anterior a la reparación). Probablemente sea de gran interés para la empresa no sólo saber que se ha reducido la proporción de defectuosos, sino también estimar a qué se ha reducido, para tener una mejor idea de lo efectiva que fue la reparación. Un intervalo de confianza del 95% para p en este caso es:

\(0.16 \pm 1.96 \sqrt{\dfrac{0.16(1-0.16)}{400}} \approx 0.16 \pm 0.036=(0.124,0.196)\)

Por lo tanto, podemos decir que los datos proporcionan evidencia de que se ha reducido la proporción de productos defectuosos, y estamos 95% seguros de que se ha reducido a algún lugar entre 12.4% y 19.6%. Esta es información muy útil, ya que nos dice que aunque los resultados fueron significativos (es decir, la reparación redujo el número de productos defectuosos), la reparación podría no haber sido lo suficientemente efectiva, si logró reducir el número de productos defectuosos solo al rango proporcionado por la confianza intervalo. Esto, por supuesto, se relaciona con la idea de significancia estadística vs. importancia práctica que discutimos anteriormente. A pesar de que los resultados son estadísticamente significativos (Ho fue rechazado), prácticamente hablando, la reparación podría considerarse ineficaz.

Aprender haciendo: pruebas de hipótesis e intervalos de confianza

Vamos a resumir

A pesar de que esta parte de la sección actual es sobre la prueba z para la proporción poblacional, está cargada de ideas muy importantes que se aplican a las pruebas de hipótesis en general. Ya hemos resumido los detalles que son específicos de la prueba z para proporciones, por lo que el propósito de este resumen es resaltar las ideas generales.

El proceso de prueba de hipótesis tiene cuatro pasos:

I. Afirmando las hipótesis nulas y alternativas (Ho y Ha).

II. Obtener una muestra aleatoria (o al menos una que pueda considerarse aleatoria) y recopilar datos. Usando los datos:

Verifique que se cumplan las condiciones bajo las cuales la prueba puede ser utilizada de manera confiable.

Resumir los datos usando un estadístico de prueba.

• El estadístico de prueba es una medida de la evidencia en los datos contra Ho. Cuanto mayor sea el estadístico de prueba en magnitud, más evidencia serán los datos presentes contra Ho.

III. Encontrar el valor p de la prueba. El valor p es la probabilidad de obtener datos como los observados (o incluso más extremos) asumiendo que la hipótesis nula es verdadera, y se calcula usando la distribución nula del estadístico de prueba. El valor p es una medida de la evidencia contra Ho. Cuanto menor es el valor p, más evidencia presentan los datos contra Ho.

IV. Elaboración de conclusiones.

Conclusiones sobre la significancia estadística de los resultados:

Si el valor p es pequeño, los datos presentan evidencia suficiente para rechazar Ho (y aceptar Ha).

Si el valor p no es pequeño, los datos no aportan pruebas suficientes para rechazar Ho.

Para ayudar a guiar nuestra decisión, utilizamos el nivel de significancia como punto de corte para lo que se considera un valor p pequeño. El límite de significancia generalmente se establece en 0.05.

A continuación, deben aportarse conclusiones en el contexto del problema.

Ideas importantes adicionales sobre las pruebas de hipótesis

• Los resultados que se basan en una muestra más grande llevan más peso, y por lo tanto a medida que aumenta el tamaño de la muestra, los resultados se vuelven más significativos estadísticamente.

• Incluso un efecto muy pequeño y prácticamente sin importancia se vuelve estadísticamente significativo con un tamaño de muestra lo suficientemente grande. Por lo tanto, siempre debe considerarse la distinción entre significancia estadística e importancia práctica.

• Se pueden utilizar intervalos de confianza para llevar a cabo pruebas de doble cara (95% de confianza para el nivel de significancia 0.05). Si el valor nulo no está incluido en el intervalo de confianza (es decir, no es uno de los valores plausibles para el parámetro), tenemos evidencia suficiente para rechazar Ho. De lo contrario, no podemos rechazar a Ho.

• Si los resultados son estadísticamente significativos, podría ser interesante hacer un seguimiento de las pruebas con un intervalo de confianza para conocer el valor real del parámetro de interés.

• Es importante tener en cuenta que existen dos tipos de errores en las pruebas de hipótesis (Tipo I y Tipo II) y que el poder de una prueba estadística es una medida importante de la probabilidad de que seamos capaces de detectar una diferencia de interés para nosotros en un problema particular.

Medios (todos los pasos)

NOTA: A partir de esta página, las actividades Aprender Haciendo y Did I Get This se presentan como archivos PDF interactivos. La interactividad puede no funcionar en dispositivos móviles o con ciertos visores de PDF. Utiliza un producto oficial de ADOBE como ADOBE READER

Si tiene algún problema con los archivos PDF interactivos Learn By Doing or Did I Get This, puede ver todas las preguntas y respuestas que se presentan en esta página en este documento:

• Pregunta/respuesta (¡ALERTA DE SPOILER!)

• Pruebas Acerca de μ (mu) Cuando σ (sigma) es desconocida — La prueba t para una media poblacional
• Paso 1: Exponer las hipótesis
• Paso 2: Obtener datos, verificar condiciones y resumir datos
• Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
• Paso 4: Conclusión
• La distribución T

Objetivos de aprendizaje

LO 4.33: En un contexto dado, distinguir entre situaciones que involucran una proporción poblacional y una media poblacional y especificar la hipótesis nula y alternativa correcta para el escenario.

CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.

Objetivos de aprendizaje

LO 6.26: Esbozar la lógica y el proceso de las pruebas de hipótesis.

Objetivos de aprendizaje

LO 6.27: Explique qué es el valor p y cómo se utiliza para sacar conclusiones.

Objetivos de aprendizaje

LO 6.30: Utilizar un intervalo de confianza para determinar la conclusión correcta de la prueba de hipótesis bilateral asociada.

Video

Video: Medios (Todos los pasos) (13:11)

Hasta el momento hemos hablado de la lógica detrás de las pruebas de hipótesis y luego ilustrado cómo procede este proceso en la práctica, utilizando la prueba z para la proporción poblacional (p).

Ahora estamos pasando a discutir las pruebas para la media poblacional (μ, mu), que es el parámetro de interés cuando la variable de interés es cuantitativa.

Algunos comentarios sobre la estructura de esta sección:

• Las bases básicas para la realización de pruebas de hipótesis ya se han sentado en nuestra discusión general y en nuestra presentación de pruebas sobre proporciones.

Por lo tanto, podemos modificar fácilmente los cuatro pasos para realizar pruebas sobre medios en su lugar, sin volver a entrar en todos los detalles.

Utilizaremos este enfoque para todas las pruebas futuras así que asegúrese de volver a la discusión en general y para que las proporciones revisen los conceptos con más detalle.

• En nuestra discusión sobre los intervalos de confianza para la media poblacional, hicimos la distinción entre si se conocía la desviación estándar poblacional, σ (sigma) o si necesitábamos estimar este valor utilizando la desviación estándar de la muestra, s.

En esta sección, solo discutiremos el segundo caso ya que en los escenarios más realistas desconocemos la desviación estándar poblacional.

En este caso necesitamos usar la distribución t- en lugar de la distribución normal estándar para los aspectos de probabilidad de intervalos de confianza (elección de valores de tabla) y pruebas de hipótesis (búsqueda de valores p).

• Aunque discutiremos algunos detalles teóricos o conceptuales para algunos de los análisis que aprenderemos, a partir de este punto nos basaremos en el software para realizar pruebas y calcular intervalos de confianza para nosotros, mientras nos enfocamos en comprender qué métodos se utilizan para qué situaciones y lo que dicen los resultados en contexto.

Si te interesa más información sobre la prueba z, donde asumimos que se conoce la desviación estándar poblacional σ (sigma), puedes revisar el Curso Abierto de Estadística de Aprendizaje Carnegie Mellon (deberás dar click en “INGRESAR CURSO”).

Como cualquier otra prueba, la prueba t para la media poblacional sigue el proceso de cuatro pasos:

• PASO 1: Afirmando las hipótesis H _o y H _a.

• PASO 2: Recopilar datos relevantes, verificar que los datos cumplan las condiciones que nos permitan utilizar esta prueba, y resumir los datos utilizando un estadístico de prueba.

• PASO 3: Encontrar el valor p de la prueba, la probabilidad de obtener datos tan extremos como los recopilados (o incluso más extremos, en la dirección de la hipótesis alternativa), asumiendo que la hipótesis nula es verdadera. En otras palabras, ¿qué tan probable es que la única razón para obtener datos como los observados sea la variabilidad del muestreo (y no porque H _o no sea cierto)?

• PASO 4: Sacar conclusiones, evaluar la significancia estadística de los resultados con base en el valor p, y exponer nuestras conclusiones en contexto. (¿Tenemos o no pruebas para rechazar H _o y aceptar H _a?)

• Nota: En la práctica, también debemos considerar siempre la significación práctica de los resultados así como la significancia estadística.

Ahora pasaremos por los cuatro pasos específicamente para la prueba t para la media poblacional y los aplicaremos a nuestros dos ejemplos.

Pruebas Acerca de μ (mu) Cuando σ (sigma) es desconocida — La prueba t para una media poblacional

Sólo en unos pocos casos es razonable suponer que la desviación estándar poblacional, σ (sigma), es conocida y por lo tanto no cubriremos pruebas de hipótesis en este caso. Se discutieron ambos casos para intervalos de confianza para que pudiéramos calcular algunos intervalos de confianza a mano.

Para esta y todas las pruebas futuras, confiaremos en el software para obtener nuestras estadísticas resumidas, estadísticas de prueba y valores p para nosotros.

El caso donde σ (sigma) es desconocido es mucho más común en la práctica. ¿Qué podemos usar para reemplazar σ (sigma)? Si no conoces la desviación estándar de la población, lo mejor que puedes hacer es encontrar la desviación estándar muestral, s, y usarla en lugar de σ (sigma). (Tenga en cuenta que esto es exactamente lo que hicimos cuando discutimos los intervalos de confianza).

¿Eso es? ¿Podemos simplemente usar s en lugar de σ (sigma), y el resto es el mismo que el caso anterior? Desafortunadamente, no es tan sencillo, pero tampoco muy complicado.

Aquí, cuando usamos la desviación estándar muestral, s, como nuestra estimación de σ (sigma) ya no podemos usar una distribución normal para encontrar el punto de corte para los intervalos de confianza o los valores p para las pruebas de hipótesis.

En su lugar debemos usar la distribución t- (con n-1 grados de libertad) para obtener el valor p para esta prueba.

Se discutió este tema para intervalos de confianza. Hablaremos más sobre la t- distribución después de discutir los detalles de esta prueba para quienes estén interesados en aprender más.

No es realmente necesario que entendamos esta distribución pero es importante que utilicemos las distribuciones correctas en la práctica a través de nuestro software.

Esperaremos hasta UNIDAD 4B para ver cómo realizar esta prueba en el software. Por ahora enfocarse en comprender el proceso y sacar las conclusiones correctas a partir de los valores p dados.

Ahora pasemos por los cuatro pasos en la realización de la prueba t para la media poblacional.

Paso 1: Exponer las hipótesis

Las hipótesis nulas y alternativas para la prueba t para la media poblacional (μ, mu) tienen exactamente la misma estructura que las hipótesis para la prueba z para la proporción poblacional (p):

La hipótesis nula tiene la forma:

• Ho: μ = μ ₀ (mu = mu_cero)

(donde μ ₀ (mu_zero) a menudo se llama el valor nulo)

La hipótesis alternativa adopta una de las siguientes tres formas (dependiendo del contexto):

• Ha: μ < μ ₀ (mu < mu_zero) (unilateral)
• Ha: μ > μ ₀ (mu > mu_zero) (unilateral)
• Ha: μ ≠ μ ₀ (mu ≠ mu_zero) (de dos caras)

donde la elección de la alternativa apropiada (de las tres) suele ser bastante clara desde el contexto del problema.

Si sientes que no está claro, lo más probable es que sea un problema bilateral. Los estudiantes suelen ser buenos para reconocer la terminología “más que” y “menos que” pero las diferencias a veces pueden ser más difíciles de detectar, a veces esto se debe a que tienes ideas preconcebidas de cómo crees que debería ser! Tampoco puedes usar la información de la muestra para ayudarte a determinar la hipótesis. No sabríamos nuestros datos cuando originalmente hicimos la pregunta.

Ahora pruébalo tú mismo. Aquí hay algunos ejercicios sobre la afirmación de las hipótesis para las pruebas para una media poblacional.

Aprender haciendo: Indicar las hipótesis para una prueba para una media poblacional

Aquí hay algunas actividades más para la práctica.

¿Conseguí esto? : Indicar las Hipótesis para una prueba para una media poblacional

Al establecer hipótesis, asegúrese de usar solo la información en la pregunta de investigación. No podemos usar nuestros datos de muestra para ayudarnos a establecer nuestras hipótesis.

Para esta prueba, sigue siendo importante elegir correctamente la hipótesis alternativa como “menor que”, “mayor que” o “diferente” aunque generalmente en la práctica se utilizan pruebas de dos muestras.

Paso 2: Obtener datos, verificar condiciones y resumir datos

Obtener datos de una muestra:

• En este paso obtendríamos datos de una muestra. Esto no es algo que hacemos mucho en los cursos pero se hace muy a menudo en la práctica!

Consulta las condiciones:

• Luego verificamos las condiciones bajo las cuales esta prueba (la prueba t para una media poblacional) puede llevarse a cabo de manera segura, que son:

• La muestra es aleatoria (o al menos puede considerarse aleatoria en contexto).

• Estamos en una de las tres situaciones marcadas con una marca de verificación verde en la siguiente tabla (que aseguran que la barra x es al menos aproximadamente normal y el estadístico de prueba usando la desviación estándar de la muestra, s, es por lo tanto una distribución t con n-1 grados de libertad — demostrando que esto está más allá del alcance de este curso):

• Para muestras grandes, no es necesario verificar la normalidad en la población. Podemos confiar en el tamaño de la muestra como base para la validez del uso de esta prueba.

• Para muestras pequeñas, necesitamos tener datos de una población normal para que los valores p y los intervalos de confianza sean válidos.

En la práctica, para muestras pequeñas, puede ser muy difícil determinar si la población es normal. Aquí hay una simulación para darle una mejor comprensión de las dificultades.

Video: Simulaciones — ¿Son muestras de una población normal? (4:58)

Ahora pruébalo tú mismo con algunas actividades.

Aprender haciendo: Comprobación de las condiciones para las pruebas de hipótesis para la media poblacional

Comentarios:

• Siempre es una buena idea mirar los datos y tener una idea de su patrón independientemente de si realmente necesitas hacerlo para evaluar si se cumplen las condiciones.
• Esta idea de mirar los datos es relevante para todas las pruebas en general. En el siguiente módulo—inferencia para relaciones— la realización de análisis exploratorios de datos antes de la inferencia será una parte integral del proceso.

Aquí hay algunos problemas más para la práctica extra.

¿Conseguí esto? : Comprobación de las condiciones para las pruebas de hipótesis para la media poblacional

Al establecer hipótesis, asegúrese de usar solo la información en la res

Calcular estadística de prueba

Suponiendo que se cumplan las condiciones, calculamos la media de la muestra x-bar y la desviación estándar de la muestra, s (que estima σ (sigma)), y resumimos los datos con un estadístico de prueba.

El estadístico de prueba para la prueba t para la media poblacional es:

\(t=\dfrac{\bar{x} - \mu_0}{s/ \sqrt{n}}\)

Recordemos que dicho estadístico de prueba estandarizado representa cuántas desviaciones estándar por encima o por debajo de μ ₀ (mu_zero) es nuestra barra x media de muestra.

Por lo tanto, nuestro estadístico de prueba es una medida de cuán diferentes son nuestros datos de lo que se afirma en la hipótesis nula. Esta es una idea que también mencionamos en la prueba anterior.

Nuevamente confiaremos en el valor p para determinar cuán inusuales serían nuestros datos si la hipótesis nula es verdadera.

Como mencionamos, el estadístico de prueba en la prueba t para una media poblacional no sigue una distribución normal estándar. Más bien, sigue otra distribución en forma de campana llamada distribución t-.

Presentaremos los detalles de esta distribución al final para los interesados pero por ahora trabajaremos en el proceso de la prueba.

Aquí hay algunos hechos importantes.

• En lenguaje estadístico decimos que la distribución nula de nuestro estadístico de prueba es la distribución t- con (n-1) grados de libertad. En otras palabras, cuando Ho es verdadero (es decir, cuando μ = μ ₀ (mu = mu_zero)), nuestro estadístico de prueba tiene una distribución t- con (n-1) d.f., y esta es la distribución bajo la cual encontramos valores p.

• Para un tamaño de muestra grande (n), la distribución nula del estadístico de prueba es aproximadamente Z, por lo que si usamos t (n — 1) o Z para calcular los valores p no hace una gran diferencia. Sin embargo, el software utilizará la distribución t independientemente del tamaño de la muestra y nosotros también.

Aunque no calcularemos los valores p a mano para esta prueba, aún podemos calcular fácilmente el estadístico de prueba.

Pruébalo tú mismo:

Aprender haciendo: Calcular el estadístico de prueba para una prueba para una media poblacional

A partir de este punto en este curso y ciertamente en la práctica vamos a permitir que el software calcule nuestras estadísticas de prueba y utilizaremos los valores p proporcionados para sacar nuestras conclusiones.

Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera

Utilizaremos software para obtener el valor p para esta (y todas las futuras) pruebas pero aquí están las imágenes que ilustran cómo se calcula el valor p en cada uno de los tres casos correspondientes a las tres elecciones para nuestra hipótesis alternativa.

Tenga en cuenta que debido a la simetría de la distribución t, para un valor dado del estadístico de prueba t, el valor p para la prueba bilateral es dos veces más grande que el valor p de cualquiera de las pruebas unilaterales. Lo mismo sucede cuando los valores p se calculan bajo la distribución t que cuando se calculan bajo la distribución Z.

mu_zero: Una distribución t (n-1) con t-scores en su eje horizontal. Se han marcado puntuaciones T de 0 y t, con t a la derecha de 0. t se ha generado a partir de un estadístico de prueba observado. El área a la derecha de t bajo la curva es el valor p. Gráfico inferior para Ha: mu no igual a mu_zero: Una distribución t (n-1) con t-scores en su eje horizontal. Se han marcado puntajes T de -|t|, 0 y |t|. -|t| está a la izquierda de 0, y |t| está a la derecha. t se ha generado a partir de un estadístico de prueba observado. La suma del área bajo la curva a la izquierda de -|t| y a la derecha de |t| es el valor p.” height="840" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...od12_means.png "title="Top Graph for Ha: mu < mu_zero: Una distribución t (n-1) con t-scores en su eje horizontal. Se han marcado puntuaciones T de 0 y t, con t a la izquierda de 0. t se ha generado a partir de un estadístico de prueba observado. El área a la izquierda de t bajo la curva es el valor p. Gráfica Media para Ha: mu > mu_zero: Una distribución t (n-1) con t-scores en su eje horizontal. Se han marcado puntuaciones T de 0 y t, con t a la derecha de 0. t se ha generado a partir de un estadístico de prueba observado. El área a la derecha de t bajo la curva es el valor p. Gráfico inferior para Ha: mu no igual a mu_zero: Una distribución t (n-1) con t-scores en su eje horizontal. Se han marcado puntajes T de -|t|, 0 y |t|. -|t| está a la izquierda de 0, y |t| está a la derecha. t se ha generado a partir de un estadístico de prueba observado. La suma del área bajo la curva a la izquierda de -|t| y a la derecha de |t| es el valor p.” width="328">

Mostraremos algunos ejemplos de valores p obtenidos del software en nuestros ejemplos. Por ahora continuemos con nuestro resumen de los pasos.

Paso 4: Conclusión

Como es habitual, con base en el valor p (y algún nivel de significancia de elección) evaluamos la significación estadística de los resultados y sacamos nuestras conclusiones en contexto.

Para revisar lo que hemos dicho antes:

Si el valor p ≤ 0.05 entonces RECHAZAMOS Ho

• Conclusión: HAY suficiente evidencia de que Ha es Verdadero

Si el valor p > 0.05 entonces FALLAMOS EN RECHAZAR Ho

• Conclusión: NO HAY suficiente evidencia de que Ha es Verdadero

Donde en lugar de Ha es Verdadero, escribimos lo que esto significa en palabras del problema, es decir, en el contexto del escenario actual.

Este paso tiene esencialmente dos sub-pasos:

(i) Con base en el valor p, determinar si los resultados son o no estadísticamente significativos (es decir, los datos presentan evidencia suficiente para rechazar Ho).

ii) Exponga sus conclusiones en el contexto del problema.

Ahora estamos listos para mirar dos ejemplos.

EJEMPLO:

Se supone que cierto medicamento recetado contiene un promedio de 250 partes por millón (ppm) de un determinado químico. Si la concentración es mayor que esta, el medicamento puede causar efectos secundarios dañinos; si es menor, el medicamento puede ser ineficaz.

El fabricante realiza una verificación para ver si la concentración media en un envío grande se ajusta al nivel objetivo de 250 ppm o no.

Se prueba una muestra aleatoria simple de 100 porciones, y se encontró que la concentración media de la muestra es 247 ppm con una desviación estándar de la muestra de 12 ppm.

Aquí hay una figura que representa este ejemplo:

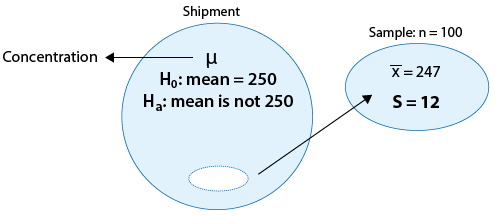
1. Las hipótesis que se están probando son:

• Ho: μ = μ ₀ (mu = mu_cero)
• Ha: μ ≠ μ ₀ (mu ≠ mu_zero)
• Donde μ = población media parte por millón del químico en todo el envío

2. Las condiciones que nos permiten utilizar la prueba t se cumplen ya que:

• La muestra es aleatoria
• El tamaño de la muestra es lo suficientemente grande como para que el Teorema del Límite Central se aplique y asegure la normalidad de la barra x. No necesitamos normalidad de la población para poder realizar esta prueba para la media poblacional. Estamos en la ^segunda columna de la tabla siguiente.

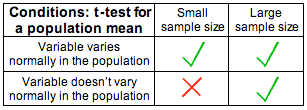
• El estadístico de prueba es:

\(t=\dfrac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\dfrac{247-250}{12 / \sqrt{100}}=-2.5\)

• Los datos (representados por la media muestral) son 2.5 errores estándar por debajo del valor nulo.

3. Encontrar el valor p.

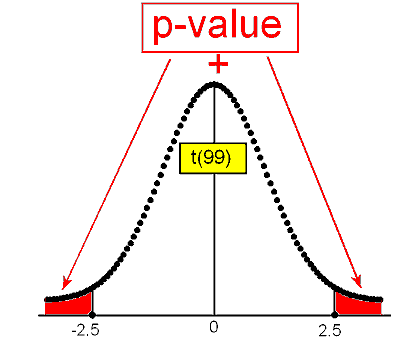
• Para encontrar el valor p utilizamos software estadístico, y calculamos un valor p de 0.014.

4. Conclusiones:

• El valor p es pequeño (.014) lo que indica que al nivel de significancia del 5%, los resultados son significativos.
• Rechazamos la hipótesis nula.
• NUESTRA CONCLUSIÓN EN CONTEX
  • Hay evidencia suficiente para concluir que la concentración media en todo el envío no es de los 250 ppm requeridos.
  • Es difícil comentar la significación práctica de este resultado sin una mayor comprensión de las consideraciones prácticas de este problema.

Aquí hay un resumen:

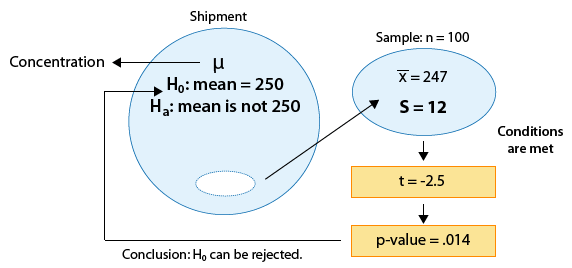
Comentarios:

• El intervalo de confianza del 95% para μ (mu) se puede usar aquí de la misma manera que para las proporciones para realizar la prueba de dos caras (comprobando si el valor nulo cae dentro o fuera del intervalo de confianza) o siguiendo una prueba t donde Ho fue rechazado para obtener información sobre el valor de μ (mu) .
• Encontramos que el intervalo de confianza del 95% es (244.619, 249.381). Ya que 250 no está en el intervalo sabemos que rechazaríamos nuestra hipótesis nula de que μ (mu) = 250. El intervalo de confianza da información adicional. Al contabilizar el error de estimación, estima que es probable que la media poblacional esté entre 244.62 y 249.38. Esto es inferior a la concentración objetivo y esa información podría ayudar a determinar la gravedad y el curso de acción adecuado en esta situación.

Precaución

En la mayoría de las situaciones en la práctica utilizamos PRUEBAS DE HIPÓTEIS DE DOS CARAS, seguidas de intervalos de confianza

Para completar la cobertura de una muestra pruebas t para una media poblacional, todavía cubrimos las tres posibles hipótesis alternativas aquí SIN EMBARGO, esta será la última prueba para la que lo haremos.

EJEMPLO:

Un estudio de investigación midió las frecuencias de pulso de 57 hombres universitarios y encontró una frecuencia media de pulso de 70 latidos por minuto con una desviación estándar de 9.85 latidos por minuto.

Los investigadores quieren saber si la frecuencia media del pulso para todos los universitarios es diferente del estándar actual de 72 latidos por minuto.

1. Las hipótesis que se están probando son:

• Ho: μ = 72
• Ha: μ ≠ 72
• Donde μ = frecuencia cardíaca media poblacional entre hombres universitarios

2. Se cumplen las condiciones que nos permiten utilizar la prueba t- ya que:

• La muestra es aleatoria.
• El tamaño muestral es grande (n = 57) por lo que no necesitamos normalidad de la población para poder realizar esta prueba para la media poblacional. Estamos en la ^segunda columna de la tabla siguiente.

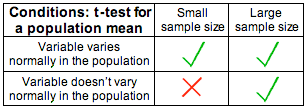
• El estadístico de prueba es:

\(t=\dfrac{\bar{x}-\mu}{s / \sqrt{n}}=\dfrac{70-72}{9.85 / \sqrt{57}}=-1.53\)

• Los datos (representados por la media muestral) son 1.53 errores estándar estimados por debajo del valor nulo.

3. Encontrar el valor p.

• Recordemos que en general el valor p se calcula bajo la distribución nula del estadístico de prueba, que, en el caso t- test, es t (n-1). En nuestro caso, en el que n = 57, el valor p se calcula bajo la distribución t (56). Utilizando software estadístico, encontramos que el valor p es 0.132.
• Así es como calculamos el valor p. http://homepage.stat.uiowa.edu/~mbognar/applets/t.html.

4. Hacer conclusiones.

• El valor p (0.132) no es pequeño, lo que indica que los resultados no son significativos.
• No podemos rechazar la hipótesis nula.
• NUESTRA CONCLUSIÓN EN CONTEX
  • No hay evidencia suficiente para concluir que la frecuencia media del pulso para todos los universitarios sea diferente del estándar actual de 72 latidos por minuto.
  • Los resultados de esta muestra no parecen tener ninguna significación práctica, ya sea con una frecuencia media de pulso de 70, esto es muy similar al valor hipotético, relativo a la variación esperada en las frecuencias de pulso.

Ahora prueba algunos tú mismo.

Aprender haciendo: Prueba de hipótesis para la media poblacional

A partir de este punto en este curso y ciertamente en la práctica vamos a permitir que el software calcule nuestra estadística de prueba y valor p y utilizaremos los valores p proporcionados para sacar nuestras conclusiones.

Con ello concluye nuestra discusión de las pruebas de hipótesis en la Unidad 4A.

En la siguiente unidad continuaremos utilizando tanto los intervalos de confianza como la prueba de hipótesis para investigar la relación entre dos variables en los casos que cubrimos en la Unidad 1 sobre análisis exploratorio de datos: veremos el Caso CQ, Caso CC y Caso QQ.

Antes de continuar, discutiremos los detalles sobre la distribución t como objeto general.

La distribución T

Hemos visto que las variables pueden ser modelizadas visualmente por muchos tipos diferentes de formas, y las llamamos distribuciones. Varias distribuciones surgen con tanta frecuencia que se les han dado nombres especiales, y se han estudiado matemáticamente.

En lo que va del curso, la única que hemos nombrado, para las variables cuantitativas continuas, es la distribución normal, pero hay otras. Uno de ellos se llama la distribución t.

La distribución t es otra distribución en forma de campana (unimodal y simétrica), como la distribución normal; y el centro de la distribución t se estandariza en cero, como el centro de la distribución normal estándar.

Al igual que todas las distribuciones que se utilizan como modelos de probabilidad, la distribución normal y la t- se escalan, por lo que el área total debajo de cada una de ellas es 1.

Entonces, ¿en qué se diferencia fundamentalmente la distribución t de la distribución normal?

• La propagación.

La siguiente imagen ilustra la diferencia fundamental entre la distribución normal y la distribución t:

Aquí tenemos una imagen que ilustra la diferencia fundamental entre la distribución normal y la distribución t:

Se puede ver en la imagen que la distribución t tiene un área ligeramente menor cerca del valor central esperado que la distribución normal, y se puede ver que la distribución t tiene correspondientemente más área en las “colas” que la distribución normal hace. (A menudo se dice que la distribución t tiene “colas más gordas” o “colas más pesadas” que la distribución normal).

Esto refleja el hecho de que la distribución t tiene una extensión mayor que la distribución normal. La misma área total de 1 se extiende sobre un rango ligeramente más amplio en la distribución t-, haciéndola un poco más baja cerca del centro en comparación con la distribución normal, y dando a la distribución t un poco más probabilidad en las 'colas' en comparación con la normal distribución.

Por lo tanto, la distribución t termina siendo el modelo apropiado en ciertos casos donde hay más variabilidad de la que sería predicha por la distribución normal. Uno de estos casos son los valores de las acciones, que tienen más variabilidad (o “volatilidad”, para usar el término económico) de lo que sería pronosticado por la distribución normal.

En realidad hay una familia entera de t- distribuciones. Todos tienen fórmulas similares (pero las matemáticas están más allá del alcance de este curso introductorio en estadística), y todas tienen colas ligeramente “más gordas” que la distribución normal. Pero algunos están más cerca de lo normal que otros.

Las t- distribuciones que tienen mayores “grados de libertad” están más cerca de lo normal (grados de libertad es un concepto matemático que no vamos a estudiar en este curso, más allá de simplemente mencionarlo aquí). Entonces, hay una distribución t “con un grado de libertad”, otra distribución t “con 2 grados de libertad” que está ligeramente más cerca de lo normal, otra distribución t “con 3 grados de libertad” que está un poco más cerca de lo normal que los anteriores, y así sucesivamente.

La siguiente imagen ilustra esta idea con solo un par de t- distribuciones (tenga en cuenta que “grados de libertad” se abrevia “d.f.” en la imagen):

El estadístico de prueba para nuestra prueba t para una media poblacional es una puntuación t que sigue una distribución t con (n — 1) grados de libertad. Recordemos que cada t- distribución está indexada de acuerdo a “grados de libertad”. Observe que, en el contexto de una prueba para una media, los grados de libertad dependen del tamaño de la muestra en el estudio.

Recuerda que dijimos que mayores grados de libertad indican que la t- distribución está más cerca de lo normal. Entonces, en el contexto de una prueba para la media, cuanto mayor sea el tamaño de la muestra, mayores serán los grados de libertad, y más cerca está la distribución t- de una distribución z normal.

Como resultado, en el contexto de una prueba para una media, el efecto de la distribución t es lo más importante para un estudio con un tamaño de muestra relativamente pequeño.

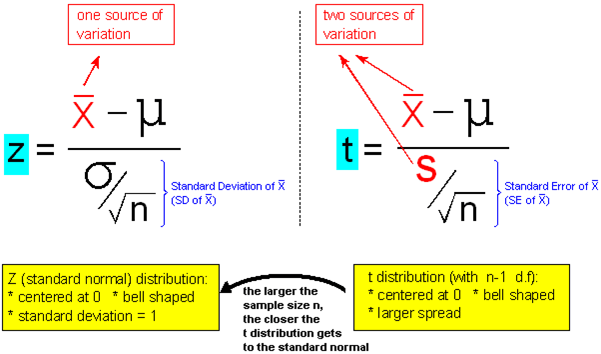
Ya terminamos de introducir la distribución t. ¿Cuáles son las implicaciones de todo esto?

• La distribución nula de nuestro estadístico de prueba t es la distribución t con (n-1) d.f. En otras palabras, cuando Ho es verdadero (es decir, cuando μ = μ ₀ (mu = mu_zero)), nuestro estadístico de prueba tiene una distribución t con (n-1) d.f., y esta es la distribución bajo la cual encontramos valores p.

• Para un tamaño de muestra grande (n), la distribución nula del estadístico de prueba es aproximadamente Z, por lo que si usamos t (n — 1) o Z para calcular los valores p no hace una gran diferencia.