7.12: Temas Misceláneos
( \newcommand{\kernel}{\mathrm{null}\,}\)
Para terminar este capítulo, tengo algunos temas que discutir que realmente no encajan con ninguna de las otras cosas de este capítulo. Todas son cosas útiles para conocer, pero en realidad son solo “temas extraños” que no encajan con los otros ejemplos. Aquí va:
problemas con la aritmética de punto flotante
Si no he aprendido nada más sobre la aritmética transfinita (y no lo he hecho) es que el infinito es un concepto tedioso e inconveniente. No sólo es molesto y contrario a veces, sino que tiene consecuencias prácticas desagradables. Como todos nos enseñaron en la secundaria, hay algunos números que no pueden representarse como un número decimal de longitud finita, ni pueden representarse como ningún tipo de fracción entre dos números enteros; √2, π y e, por ejemplo. En la vida cotidiana en su mayoría no nos importa esto. Estoy perfectamente feliz de aproximar π como 3.14, francamente. Claro, esto produce algunos errores de redondeo de vez en cuando, y si hubiera usado una aproximación más detallada como 3.1415926535 sería menos probable que me encontrara con esos problemas, pero con toda honestidad nunca he necesitado que mis cálculos sean tan precisos. En otras palabras, aunque nuestros cálculos a lápiz y papel no pueden representar el número π exactamente como un número decimal, los humanos somos lo suficientemente inteligentes como para darnos cuenta de que no nos importa. Las computadoras, desafortunadamente, son tontas... y no hay que cavar demasiado profundo para toparse con algunos temas muy raros que surgen porque no pueden representar los números a la perfección. Aquí está mi ejemplo favorito:
0.1 + 0.2 == 0.3## [1] FALSEObviamente, R ha cometido un error aquí, porque esta es definitivamente la respuesta equivocada. Tu primer pensamiento podría ser que R está roto, y podrías estar considerando cambiarte a algún otro idioma. Pero puedes reproducir el mismo error en docenas de lenguajes de programación diferentes, así que el problema no es específico de R. Tu siguiente pensamiento podría ser que es algo en el hardware, pero puedes obtener el mismo error en cualquier máquina. Es algo más profundo que eso.
El tema fundamental que nos ocupa es la aritmética de punto flotante, que es una forma elegante de decir que las computadoras siempre redondearán un número a un número fijo de dígitos significativos. El número exacto de dígitos significativos que la computadora almacena no es importante para nosotros: 130 lo que importa es que siempre que el número que la computadora está tratando de almacenar es muy largo, se obtienen errores de redondeo. Eso es en realidad lo que está pasando con nuestro ejemplo anterior. Hay pequeños errores de redondeo que han aparecido en el almacenamiento de los números por parte de la computadora, y estos errores de redondeo a su vez han provocado que el almacenamiento interno de 0.1 + 0.2 sea un poco diferente del almacenamiento interno de 0.3. ¿Qué tan grandes son estas diferencias? Preguntémosle a R:
0.1 + 0.2 - 0.3
## [1] 5.551115e-17Muy minúscula en efecto. A ninguna persona cuerda le importarían diferencias tan pequeñas. Pero R no es una persona cuerda, y el operador de igualdad == tiene una mentalidad muy literal. Devuelve un valor de VERDADERO sólo cuando los dos valores que se le da son absolutamente idénticos entre sí. Y en este caso no lo son. Sin embargo, esto solo responde a la mitad de la pregunta. La otra mitad de la pregunta es, ¿por qué estamos obteniendo estos errores de redondeo cuando solo estamos usando números simples agradables como 0.1, 0.2 y 0.3? Esto parece un poco contrario a la intuición. La respuesta es que, como la mayoría de los lenguajes de programación, R no almacena números usando su expansión decimal (es decir, base 10: usando dígitos 0, 1, 2..., 9). A los humanos nos gusta escribir nuestros números en base 10 porque tenemos 10 dedos. Pero las computadoras no tienen dedos, tienen transistores; y los transistores están construidos para almacenar 2 números no 10. Entonces puedes ver a dónde va esto: el almacenamiento interno de un número en R se basa en su expansión binaria (es decir, base 2: usando los dígitos 0 y 1). Y desafortunadamente, así es como se ve la expansión binaria de 0.1:
.1 (decimal) =.00011001100110011... (binario)
y el patrón continúa para siempre. Es decir, desde la perspectiva de su computadora, a la que le gusta codificar números en binario, 131 0.1 no es un número simple en absoluto. Para una computadora, ¡0.1 es en realidad un número binario infinitamente largo! Como consecuencia, la computadora puede cometer errores menores al hacer cálculos aquí.
Con un poco de suerte ahora entiendes el problema, que en última instancia se reduce al hecho gemelo de que (1) solemos pensar en números decimales y las computadoras suelen computar con números binarios, y (2) las computadoras son máquinas finitas y no pueden almacenar números infinitamente largos. Las únicas preguntas que quedan son cuándo debes importarte y qué debes hacer al respecto. Agradecidamente, no tiene que importarle muy a menudo: debido a que los errores de redondeo son pequeños, la única situación práctica para la que he visto surgir este problema es cuando quieres probar si un hecho aritmético sostiene exactamente que los números son idénticos (por ejemplo, es el tiempo de respuesta de alguien igual a exactamente 2×0.33 segundos?) Esto es bastante raro en el análisis de datos del mundo real, pero por si acaso ocurre, es mejor usar una prueba que permita una pequeña tolerancia. Es decir, si la diferencia entre los dos números está por debajo de un cierto valor umbral, los consideramos iguales para todos los fines prácticos. Por ejemplo, podrías hacer algo como esto, que pregunta si la diferencia entre los dos números es menor que una tolerancia de 10−10
abs( 0.1 + 0.2 - 0.3 ) < 10^-10## [1] TRUEPara hacer frente a este problema, existe una función llamada all.equal () que le permite probar la igualdad pero permite una pequeña tolerancia para los errores de redondeo:
all.equal( 0.1 + 0.2, 0.3 )## [1] TRUEregla de reciclaje
Hay una cosa que no he mencionado sobre cómo funciona la aritmética vectorial en R, y esa es la regla del reciclaje. La forma más fácil de explicarlo es dando un ejemplo sencillo. Supongamos que tengo dos vectores de diferente longitud, x e y, y quiero sumarlos juntos. No es obvio lo que eso realmente significa, así que echemos un vistazo a lo que hace R:
x <- c( 1,1,1,1,1,1 ) # x is length 6
y <- c( 0,1 ) # y is length 2
x + y # now add them:## [1] 1 2 1 2 1 2Como se puede ver al mirar esta salida, lo que R ha hecho es “reciclar” el valor del vector más corto (en este caso y) varias veces. Es decir, el primer elemento de x se agrega al primer elemento de y, y el segundo elemento de x se agrega al segundo elemento de y. Sin embargo, cuando R alcanza el tercer elemento de x no hay ningún elemento correspondiente en y, por lo que vuelve al principio: así, el tercer elemento de x se agrega al primer elemento de y. Este proceso continúa hasta que R alcanza el último elemento de x. Y eso es todo lo que hay de verdad. La misma regla de reciclaje también se aplica para la resta, la multiplicación y la división. La única otra cosa que debo señalar es que, si la longitud del vector más largo no es un múltiplo exacto de la longitud del más corto, R todavía lo hace, pero también te da un mensaje de advertencia:
x <- c( 1,1,1,1,1 ) # x is length 5
y <- c( 0,1 ) # y is length 2
x + y # now add them:
## Warning in x + y: longer object length is not a multiple of shorter object
## length## [1] 1 2 1 2 1introducción a los entornos
En esta sección quiero hacer una pregunta ligeramente diferente: ¿cuál es exactamente el espacio de trabajo? Esta pregunta parece simple, pero le queda bastante. Esta sección se puede omitir si realmente no te interesan los detalles técnicos. En la descripción que di anteriormente, hablé del espacio de trabajo como una ubicación abstracta en la que se almacenan las variables R. Eso es básicamente cierto, pero esconde un par de detalles clave. Por ejemplo, cada vez que tienes R abierto, tiene que almacenar muchas cosas en la memoria de la computadora, no solo tus variables. Por ejemplo, la función who () que escribí tiene que ser almacenada en la memoria en alguna parte, ¿verdad? Si no fuera yo no podría usarlo. Eso es bastante obvio. Pero igualmente obviamente tampoco está en el espacio de trabajo, ¡de lo contrario deberías haberlo visto! Esto es lo que está sucediendo. R necesita hacer un seguimiento de muchas cosas diferentes, así que lo que hace es organizarlas en entornos, cada uno de los cuales puede contener muchas variables y funciones diferentes. Tu espacio de trabajo es uno de esos entornos. Cada paquete que has cargado es otro entorno. Y cada vez que llamas a una función, R crea brevemente un entorno temporal en el que la función misma puede funcionar, que luego se elimina una vez que se completan los cálculos. Entonces, cuando escribo search () en la línea de comandos
search()## [1] ".GlobalEnv" "package:lsr" "package:stats"
## [4] "package:graphics" "package:grDevices" "package:utils"
## [7] "package:datasets" "package:methods" "Autoloads"
## [10] "package:base"lo que en realidad estoy viendo es una secuencia de entornos. El primero, “.globalEnv” es el nombre técnicamente correcto para tu espacio de trabajo. Nadie realmente lo llama así: o se llama el espacio de trabajo o el entorno global. Y así cuando escribas objetos () o who () lo que realmente estás haciendo es enumerar el contenido de “.globalEnv”. Pero no hay razón por la que no podamos buscar el contenido de estos otros entornos usando la función objects () (actualmente who () no soporta esto). Sólo tienes que ser un poco más explícito a tus órdenes. Si quisiera averiguar qué hay en el entorno package:stats (es decir, el entorno en el que se ha cargado el contenido del paquete stats), esto es lo que obtendría
head(objects("package:stats"))## [1] "acf" "acf2AR" "add.scope" "add1" "addmargins"
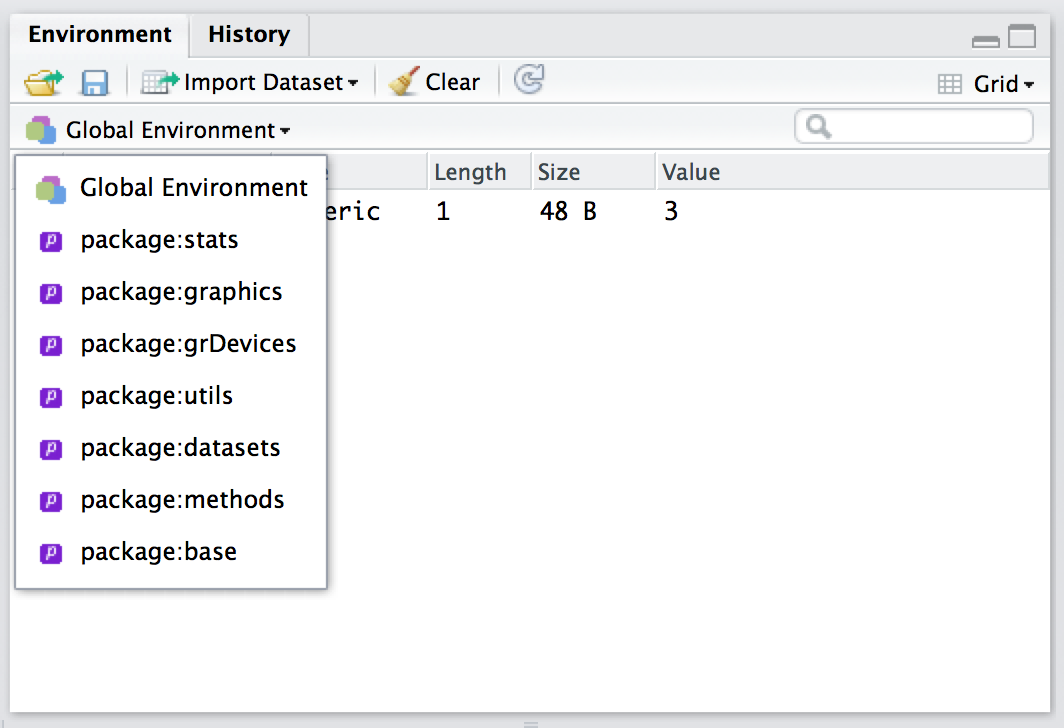
## [6] "aggregate"donde esta vez he usado head () para ocultar mucha salida porque el paquete stats contiene alrededor de 500 funciones. De hecho, en realidad puedes usar el panel de entorno en Rstudio para navegar por cualquiera de tus paquetes cargados (simplemente haz clic en el texto que dice “Global Environment” y verás un menú desplegable como el que se muestra en la Figura 7.2). La clave para entender entonces, es que se puede acceder a cualquiera de las variables R y funciones que se almacenan en uno de estos entornos, precisamente porque esos son los entornos que ha cargado! 132
Adjuntar un marco de datos
Lo último que quiero mencionar en esta sección es la función attach (), a la que a menudo se ve referida en los libros introductorios de R. Siempre que se introduce, el autor del libro suele mencionar que la función attach () se puede utilizar para “adjuntar” el marco de datos a la ruta de búsqueda, por lo que no es necesario usar el operador $. Es decir, si uso el comando attach (df) para adjuntar mi marco de datos, ya no necesito escribir df$variable, y en su lugar solo puedo escribir variable. Esto es cierto hasta donde va, pero es muy engañoso y los usuarios novatos a menudo se descarrian por esta descripción, porque esconde muchos detalles críticos.
Aquí está la descripción muy abreviada: cuando usas la función attach (), lo que hace R es crear un entorno completamente nuevo en la ruta de búsqueda, al igual que cuando cargas un paquete. Entonces, lo que hace es copiar todas las variables en su marco de datos en este nuevo entorno. Sin embargo, cuando haces esto, terminas con dos versiones completamente diferentes de todas tus variables: una en el marco de datos original y otra en el nuevo entorno. Siempre que haces una declaración como df$variable estás trabajando con la variable dentro del marco de datos; pero cuando solo escribas variable estás trabajando con la copia en el nuevo entorno. Y aquí está la parte que realmente molesta a los nuevos usuarios: los cambios a una versión no se reflejan en la otra versión. Como consecuencia, es muy fácil para R terminar con un valor diferente almacenado en las dos ubicaciones diferentes, y terminas realmente confundido como resultado.
Para ser justos con los escritores de la función attach (), la documentación de ayuda en realidad indica todo esto de manera bastante explícita, e incluso dan algunos ejemplos de cómo esto puede causar confusión al final de la página de ayuda. Y en realidad puedo ver cómo puede ser muy útil crear copias de tus datos en una ubicación separada (por ejemplo, te permite hacer todo tipo de modificaciones y eliminaciones a los datos sin tener que tocar el marco de datos original). Sin embargo, no creo que sea útil para los nuevos usuarios, ya que significa que hay que tener mucho cuidado para hacer un seguimiento de qué copia está hablando. Como consecuencia de todo esto, a los efectos de este libro he decidido no utilizar la función attach (). Es algo que puedes investigar una vez que te sientas un poco más seguro con R, pero no lo haré aquí.


